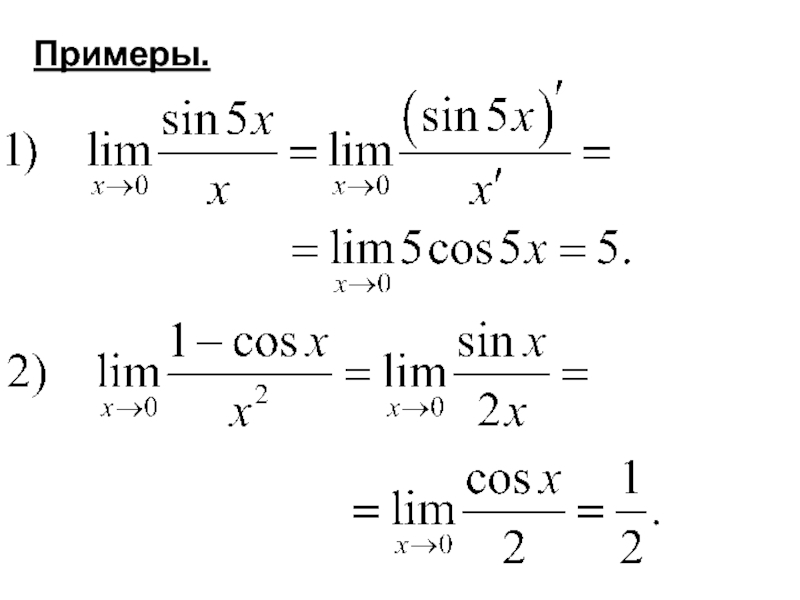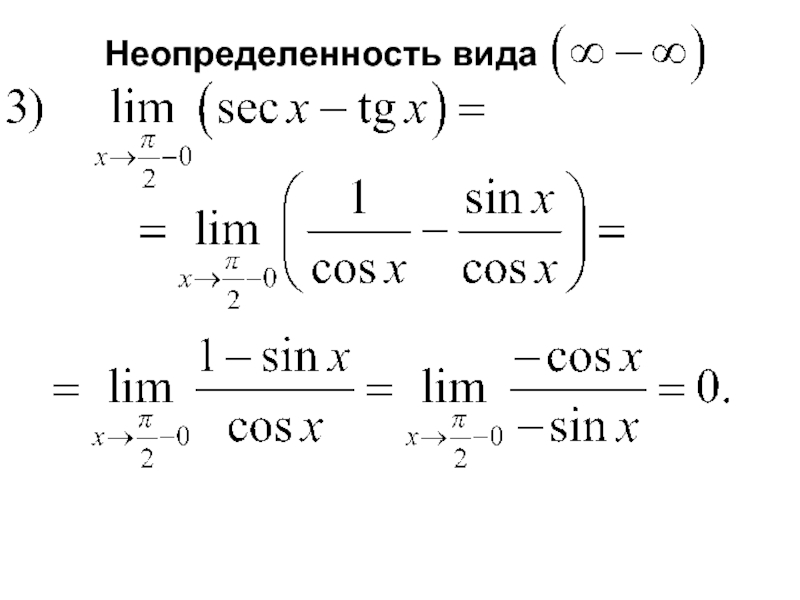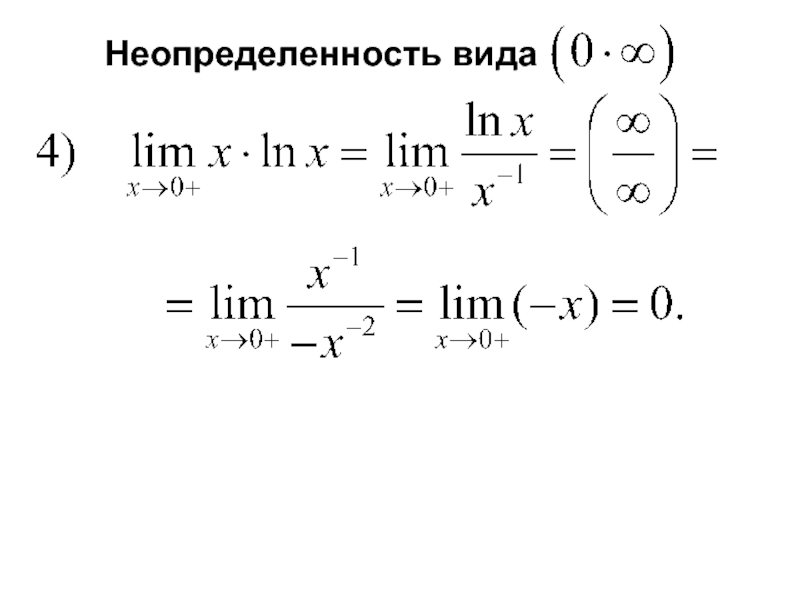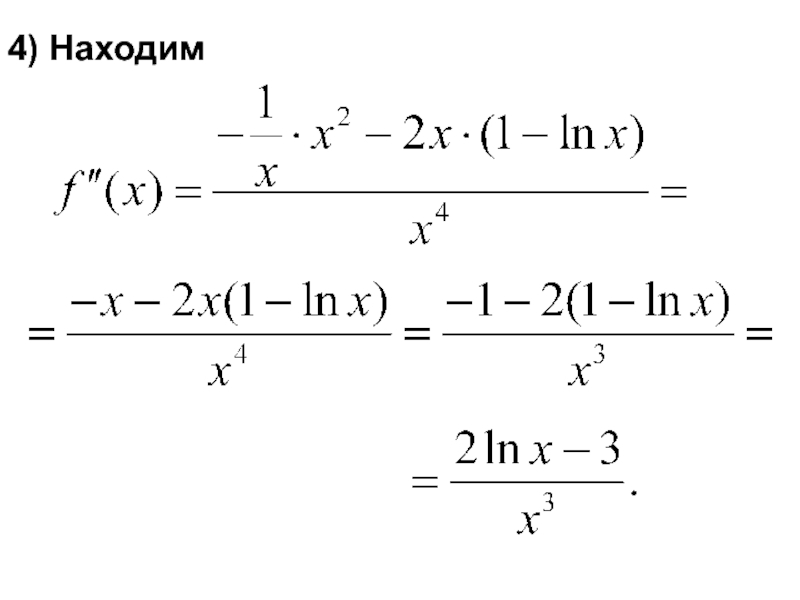- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правило Лопиталя презентация
Содержание
- 1. Правило Лопиталя
- 2. Правило Лопиталя используется для раскрытия неопределенностей или
- 3. Теорема. Пусть
- 4. Примеры.
- 5. Неопределенность вида
- 6. Неопределенность вида
- 7. Неопределенности вида Обозначим
- 8. Логарифмируя, находим Так как при
- 9. Т.к.
- 10. Отыскание наибольшего и наименьшего значений функции Правило
- 11. Пример. Найти наибольшее и наименьшее значение функции
- 12. Вычисляем значения на концах отрезка:
- 13. Пример. Построить график функции 1) Область определения:
- 14. Найдем наклонную асимптоту. (при нахождении пределов мы воспользовались правилом Лопиталя)
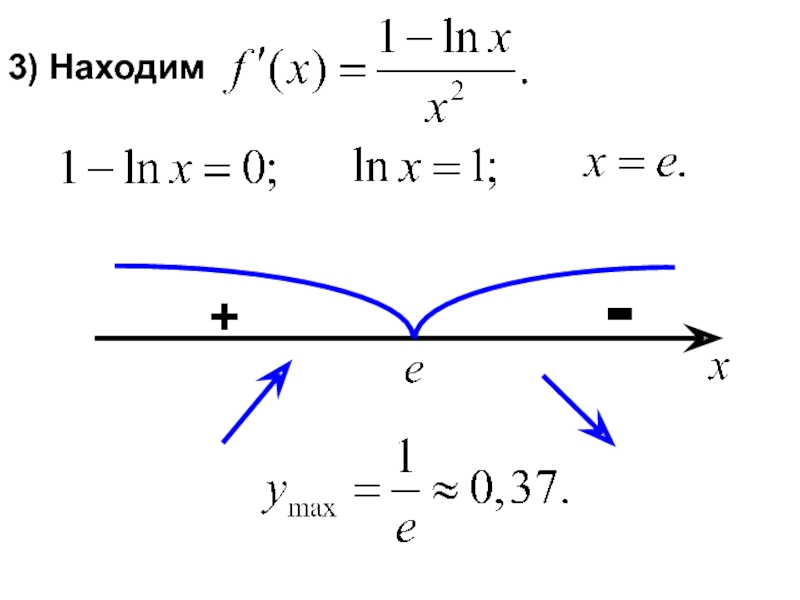
- 15. 3) Находим + -
- 16. 4) Находим
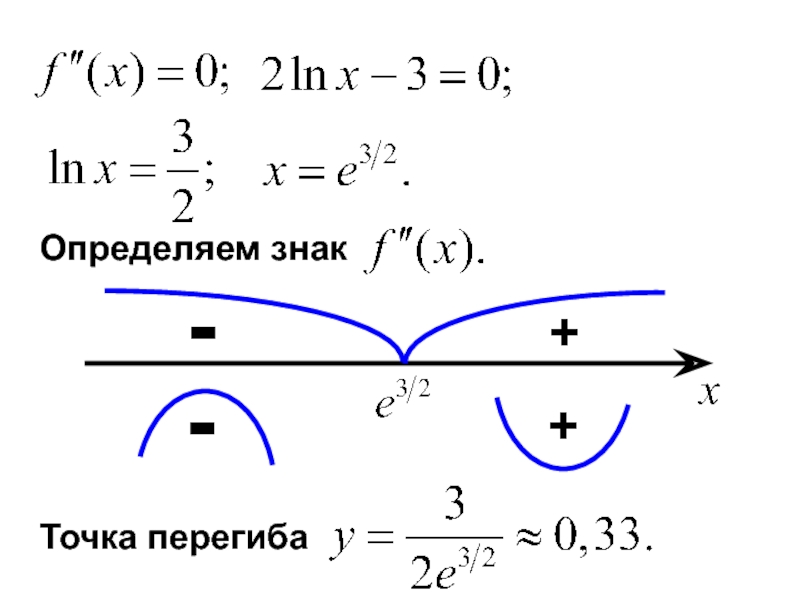
- 17. Определяем знак + - + - Точка перегиба
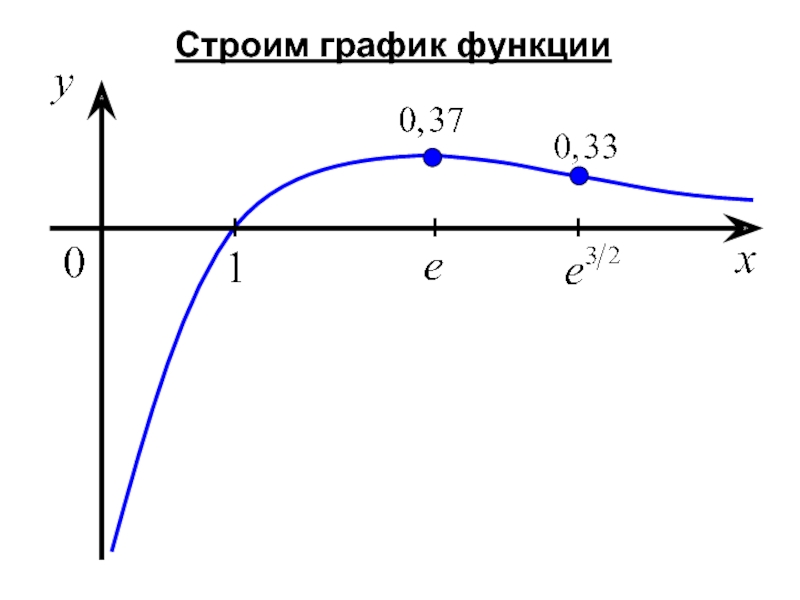
- 18. Строим график функции
Правило Лопиталя используется для раскрытия неопределенностей или
Слайд 3Теорема. Пусть и
- функции, дифференцируемые в некотором полуинтервале причем
Пусть при обе эти функции стремятся к нулю, или обе стремятся к бесконечности.
В таком случае
Слайд 8Логарифмируя, находим
Так как при
числитель и знаменатель стремятся к бесконечности,
то получаем неопределенность
то получаем неопределенность
Слайд 10Отыскание наибольшего и наименьшего значений функции
Правило нахождения наибольшего и наименьшего значения
функции на отрезке
1. Находим все критические точки функции в интервале и вычисляем в них значения функции.
2. Вычисляем значения функции на концах отрезка
3. Из всех значений выбираем наибольшее и наименьшее.
Слайд 11Пример. Найти наибольшее и наименьшее значение функции
на отрезке
Находим критические точки функции в интервале
Находим значения функции в этих точках:
