- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многогранники презентация
Содержание
- 1. Правильные многогранники
- 2. Определение. Выпуклый многогранник называется правильным, если все
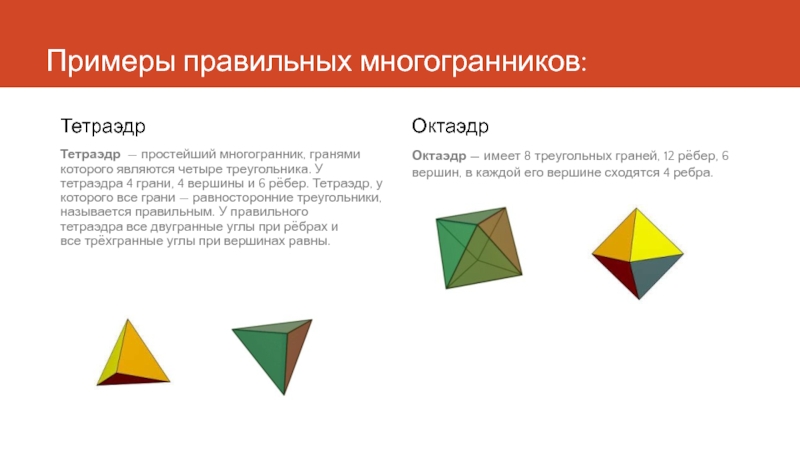
- 3. Примеры правильных многогранников: Тетраэдр Тетраэдр — простейший многогранник,
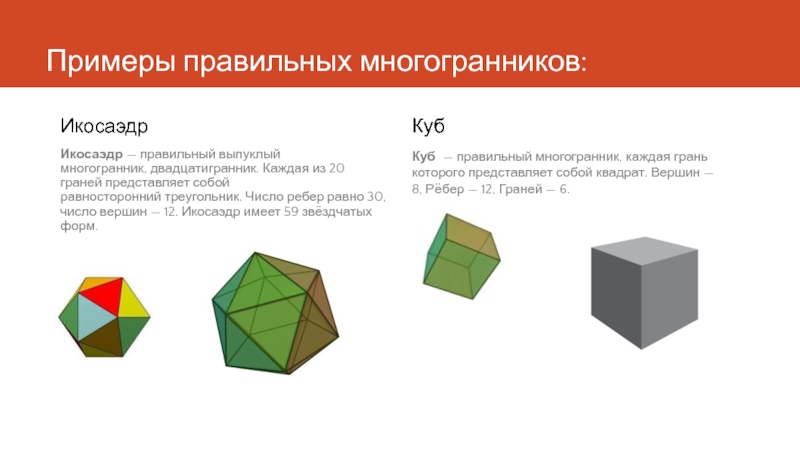
- 4. Примеры правильных многогранников: Икосаэдр Икосаэдр — правильный выпуклый
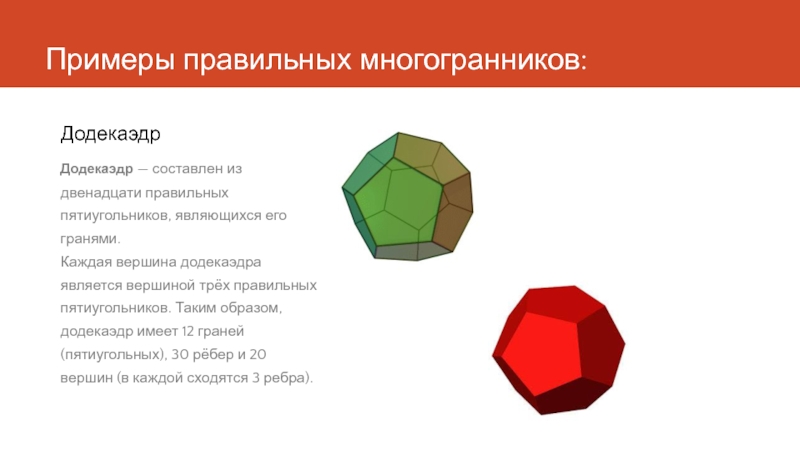
- 5. Примеры правильных многогранников: Додекаэдр Додекаэдр — составлен из
- 6. Характеристики и формулы:
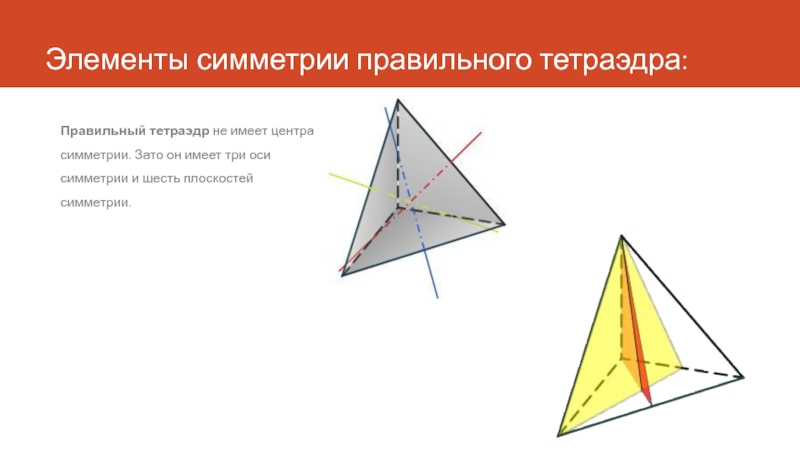
- 7. Элементы симметрии правильного тетраэдра: Правильный тетраэдр не имеет
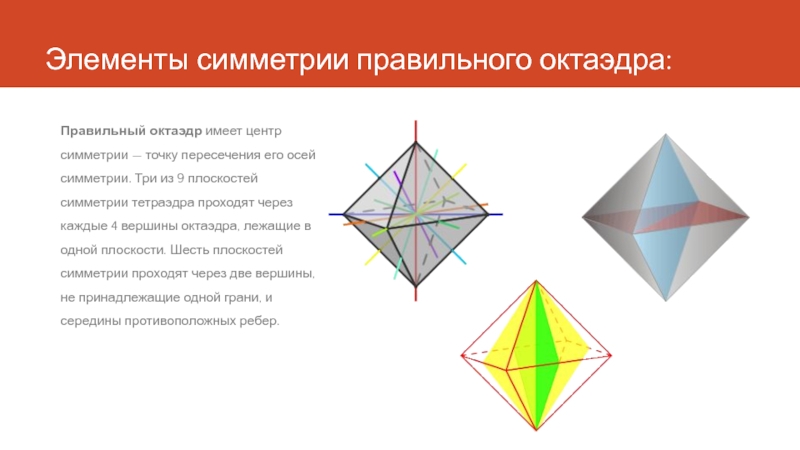
- 8. Элементы симметрии правильного октаэдра: Правильный октаэдр имеет
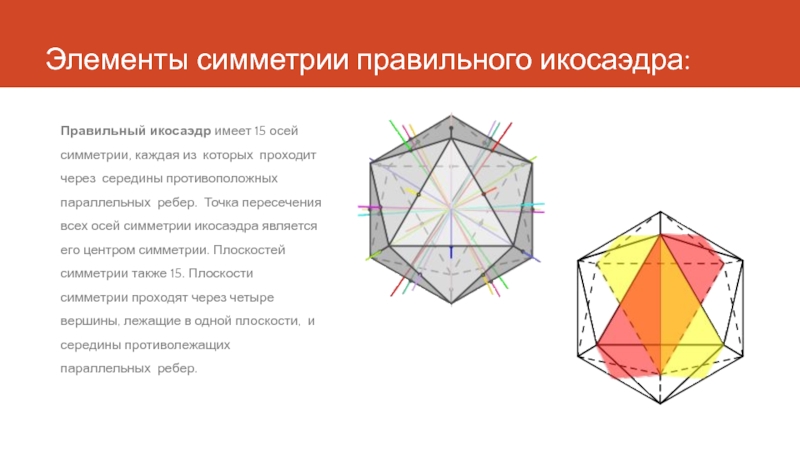
- 9. Элементы симметрии правильного икосаэдра: Правильный икосаэдр имеет
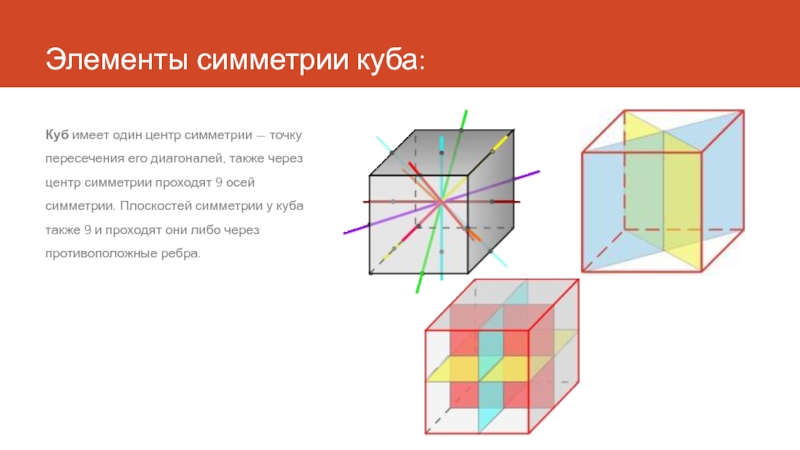
- 10. Элементы симметрии куба: Куб имеет один центр
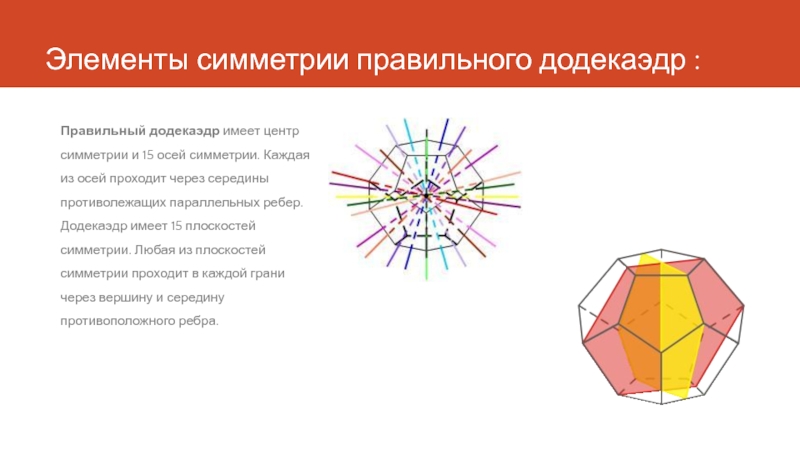
- 11. Элементы симметрии правильного додекаэдр : Правильный додекаэдр
- 12. Вся информация взята из: http://licey102.k26.ru/ http://math4school.ru wikipedia.org Учебник за 10-11 класс по геометрии
- 13. Конец.
Слайд 2Определение.
Выпуклый многогранник называется правильным, если все его грани – равные правильные
Слайд 3Примеры правильных многогранников:
Тетраэдр
Тетраэдр — простейший многогранник, гранями которого являются четыре треугольника. У
Октаэдр
Октаэдр — имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Слайд 4Примеры правильных многогранников:
Икосаэдр
Икосаэдр — правильный выпуклый многогранник, двадцатигранник. Каждая из 20 граней представляет
Куб
Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Вершин — 8, Рёбер — 12, Граней — 6.