- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Практические способы построения параллельных прямых презентация
Содержание
- 1. Практические способы построения параллельных прямых
- 2. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ Повторим определение Две прямые на плоскости называются параллельными, если они не пересекаются.
- 3. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ Обозначение a ║ b b a
- 4. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ Стр23. Две прямые перпендикулярные
- 5. УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ
- 6. УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ
- 7. УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ
- 8. УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ
- 9. УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ
- 10. УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ
- 11. УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ
- 12. УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ
- 13. ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ
- 14. ВТОРОЙ ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ ТЕОРЕМА
- 15. ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ СООТВЕТСТВЕННЫЕ УГЛЫ РАВНЫ, ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
- 16. ТРЕТИЙ ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ ТЕОРЕМА
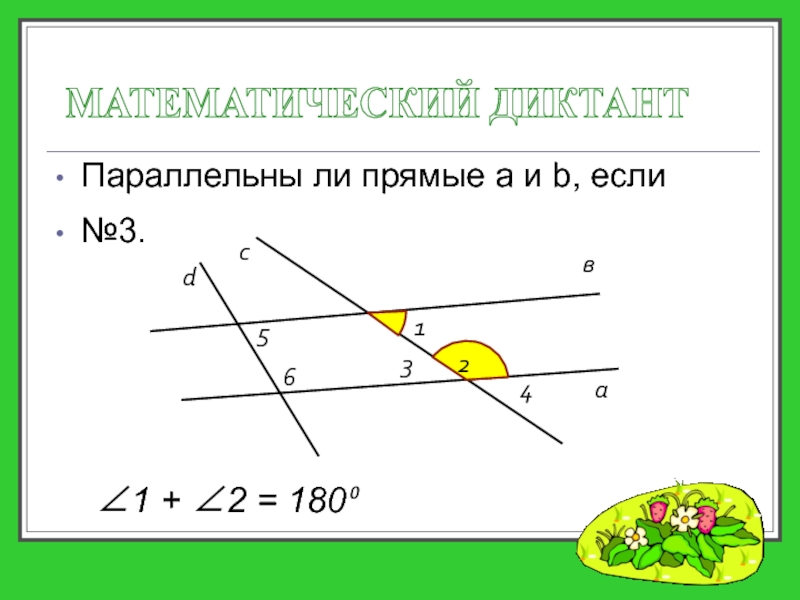
- 17. ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ CУММА ОДНОСТОРОННИХ УГЛОВ РАВНА 180⁰, ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
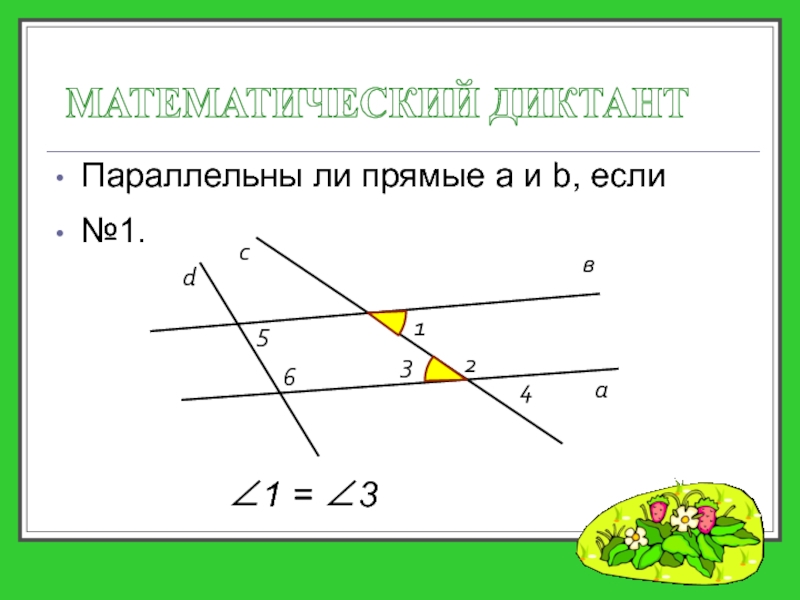
- 18. Параллельны ли прямые a и b, если
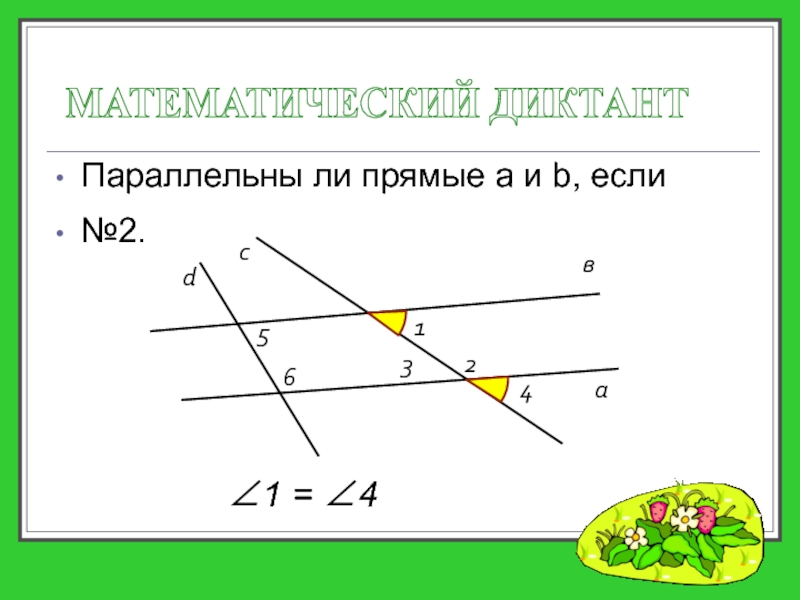
- 19. Параллельны ли прямые a и b, если
- 20. Параллельны ли прямые a и b, если
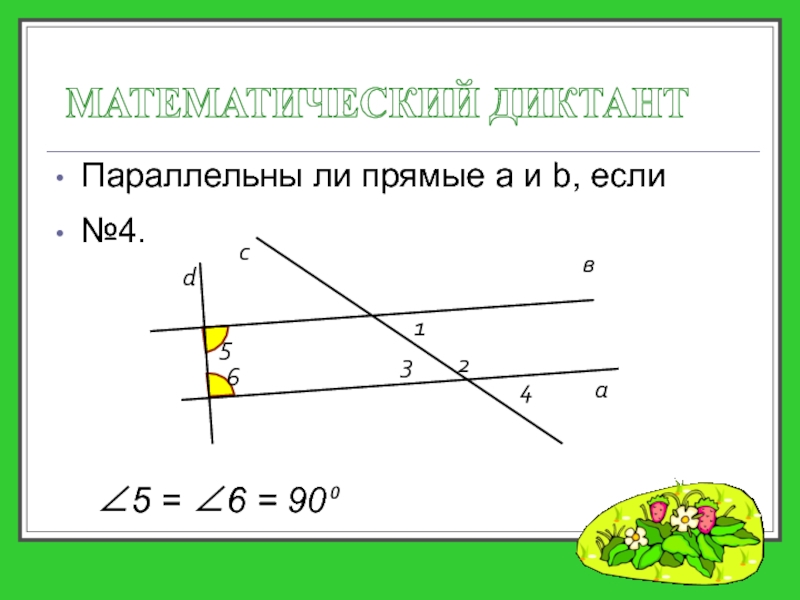
- 21. Параллельны ли прямые a и
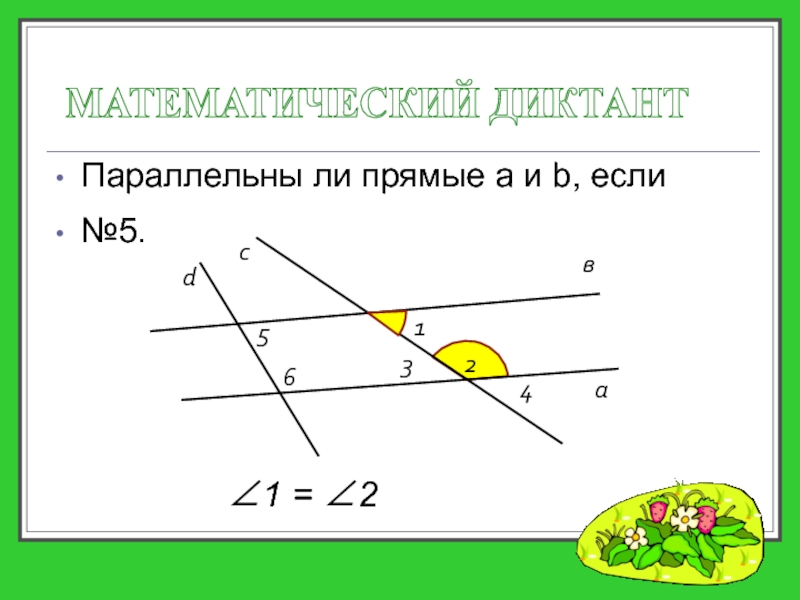
- 22. Параллельны ли прямые a и b,
- 23. №1. Да №2. Да №3. Да. №4.
- 24. Построение С помощью угольника и линейки
- 25. №1. С помощью угольника и линейки проведите 5 параллельных прямых. ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
- 26. №2. С помощью угольника и линейки через
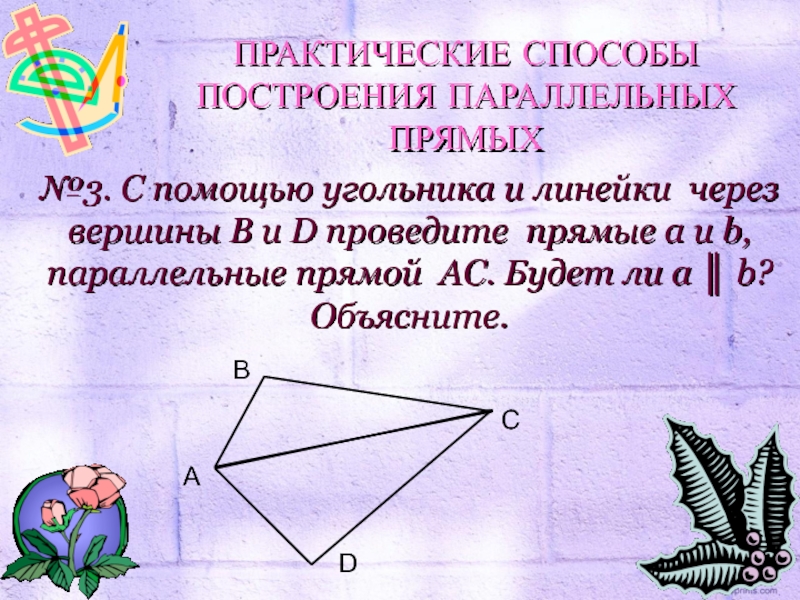
- 27. №3. С помощью угольника и линейки через
- 28. №4. С помощью угольника и линейки через
- 29. №5. С помощью циркуля и линейки через
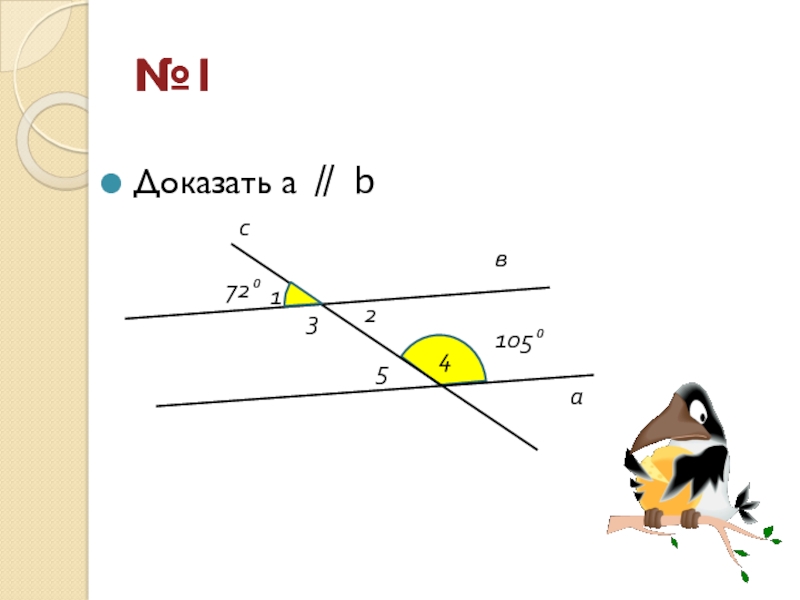
- 30. Доказать a ∥ b а с
- 31. №2 Доказать ME ∥ BD
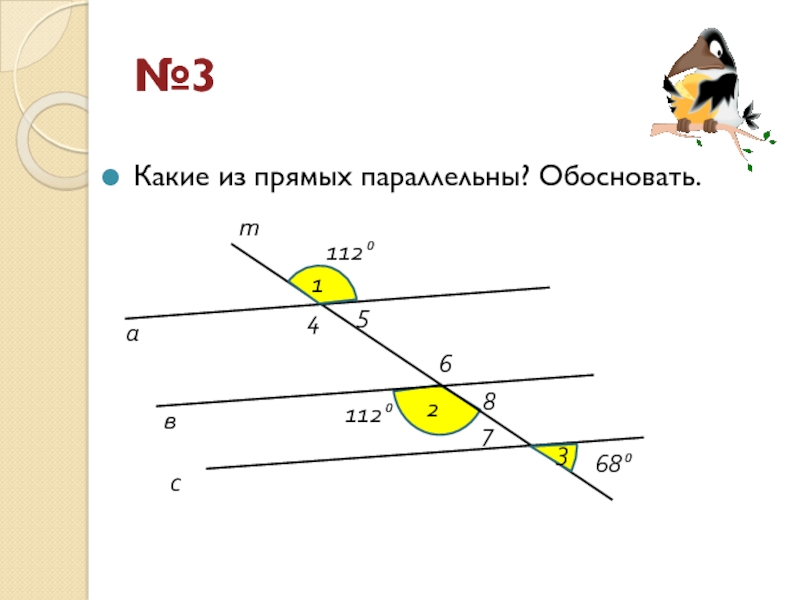
- 32. Какие из прямых параллельны? Обосновать.
- 33. П. 26 вопросы 1-6 (стр.68) Запиши решения всех задач, рассмотренных в презентации. Задание на дом
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ Повторим определение Две прямые на плоскости называются параллельными, если они не пересекаются.
Слайд 2ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Повторим определение
Две прямые на плоскости называются параллельными, если они не
пересекаются.
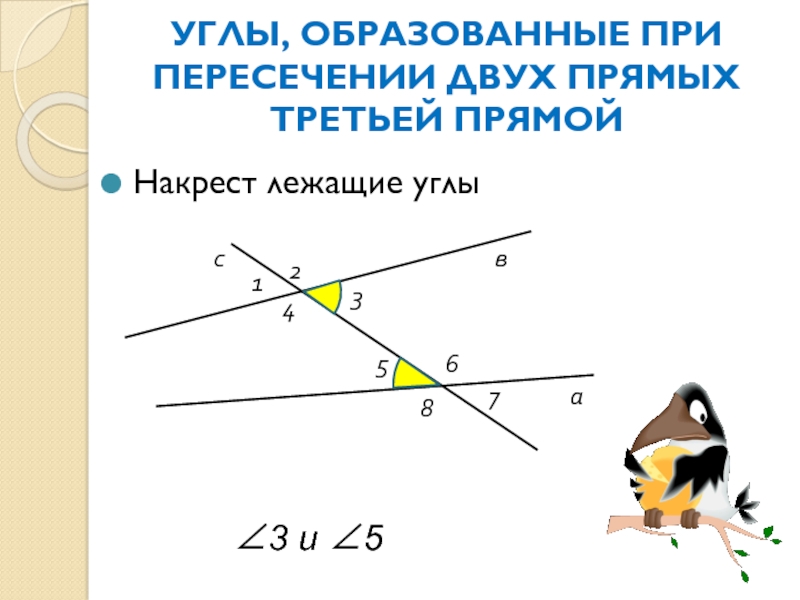
Слайд 5УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Накрест лежащие углы
а
с
в
1
2
3
4
5
6
7
8
∠3 и
∠5
Слайд 6УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Накрест лежащие углы
а
с
в
1
2
3
4
5
6
7
8
∠4 и
∠6
Слайд 7УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Односторонние углы
а
с
в
1
2
3
4
5
6
7
8
∠4 и ∠5
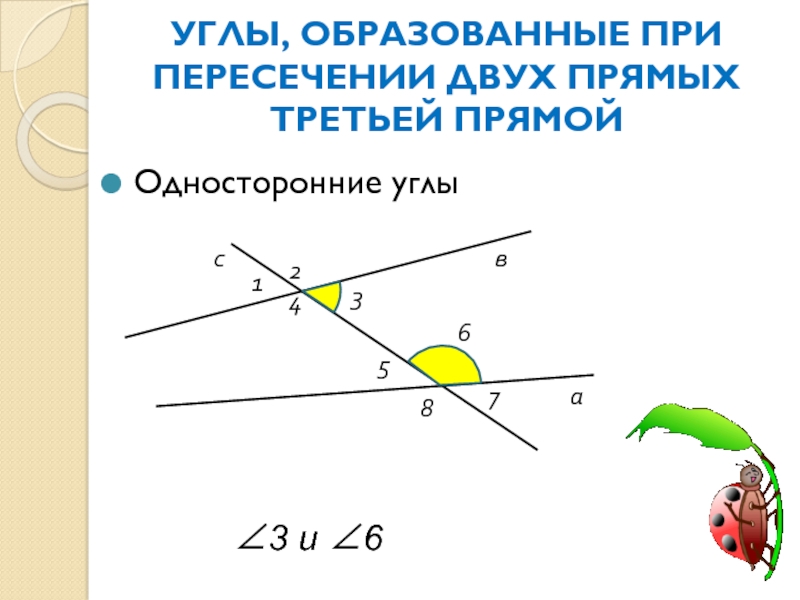
Слайд 8УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Односторонние углы
а
с
в
1
2
3
4
5
6
7
8
∠3 и ∠6
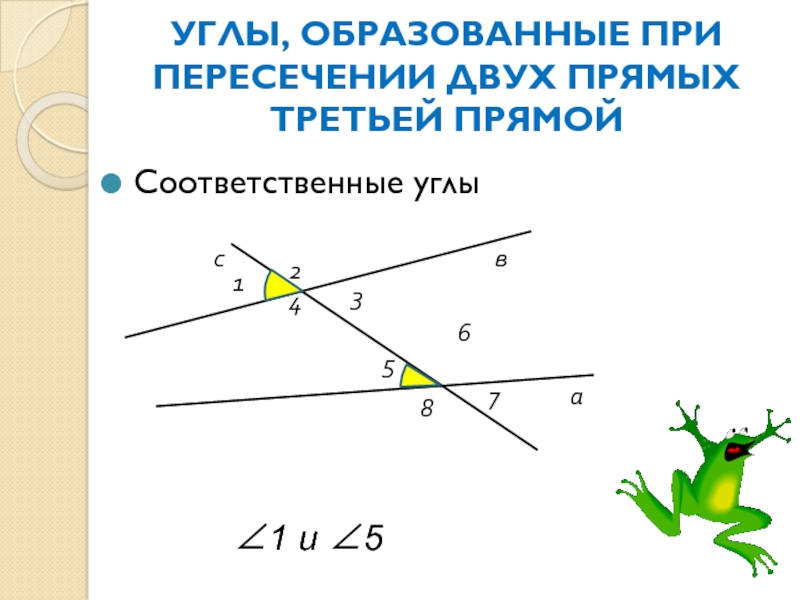
Слайд 9УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Соответственные углы
а
с
в
1
2
3
4
5
6
7
8
∠1 и ∠5
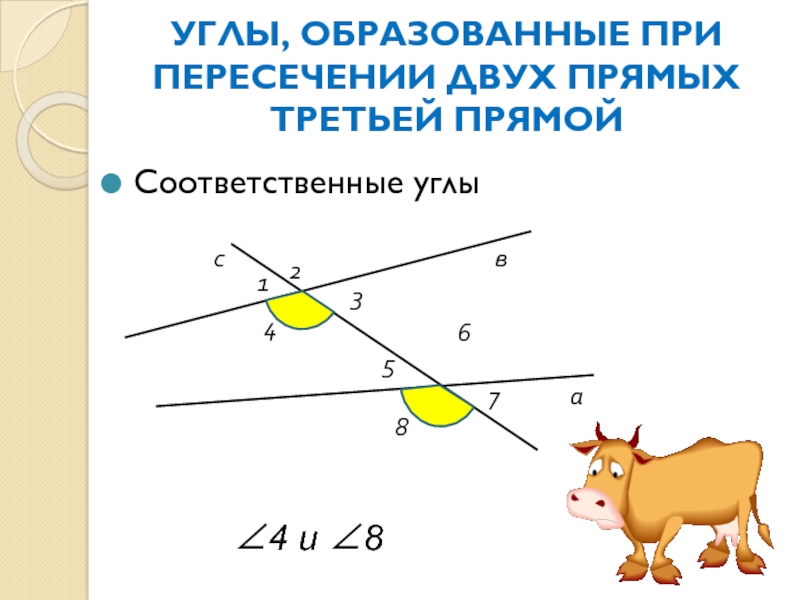
Слайд 10УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Соответственные углы
а
с
в
1
2
3
4
5
6
7
8
∠4 и ∠8
Слайд 11УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Соответственные углы
а
с
в
1
2
3
4
5
6
7
8
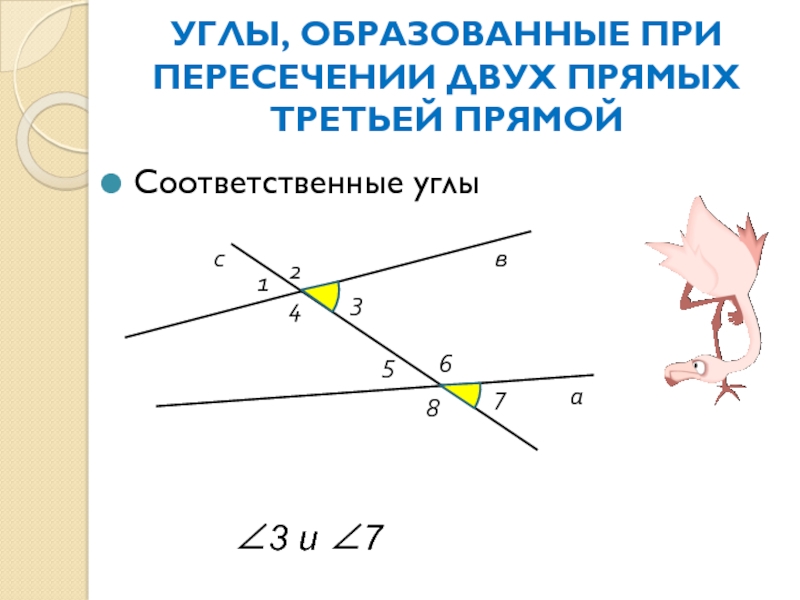
∠3 и ∠7
Слайд 12УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Соответственные углы
а
с
в
1
2
3
4
5
6
7
8
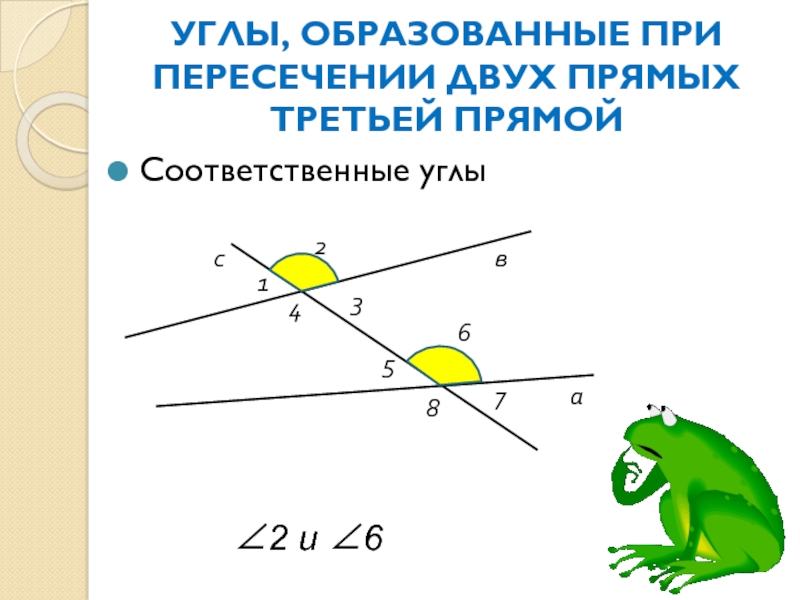
∠2 и ∠6
Слайд 13ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ НАКРЕСТ ЛЕЖАЩИЕ
УГЛЫ РАВНЫ, ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
Слайд 17ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ CУММА ОДНОСТОРОННИХ УГЛОВ РАВНА 180⁰,
ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
Слайд 24Построение
С помощью угольника и линейки
а
b
B
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
Слайд 25№1. С помощью угольника и линейки проведите 5 параллельных прямых.
ПРАКТИЧЕСКИЕ СПОСОБЫ
ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
Слайд 26№2. С помощью угольника и линейки через точки A и B
проведите прямые, параллельные прямой a.
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
a
B
A
Слайд 27№3. С помощью угольника и линейки через вершины B и D
проведите прямые a и b, параллельные прямой AC. Будет ли a ║ b? Объясните.
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
B
A
C
D
Слайд 28№4. С помощью угольника и линейки через вершины A, B и
C проведите прямые a, b и c, параллельные прямой l. Параллельны ли эти прямые между собой? Пересечет ли прямая AC прямую l? Объясните.
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
B
A
C
l
Слайд 29№5. С помощью циркуля и линейки через вершину С треугольника ABC
проведите прямую параллельную AB.
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
Слайд 33П. 26 вопросы 1-6 (стр.68)
Запиши решения всех задач, рассмотренных в презентации.
Задание
на дом
