Поворот. Параллельный перенос презентация

Содержание

1. Поворот. Параллельный перенос
2. «Без движения — жизнь только летаргический сон». Жан Жак Руссо
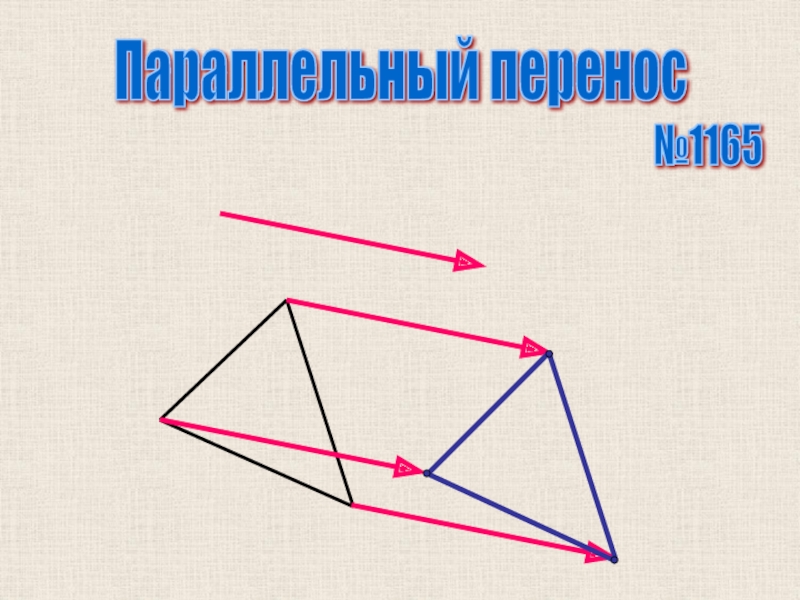
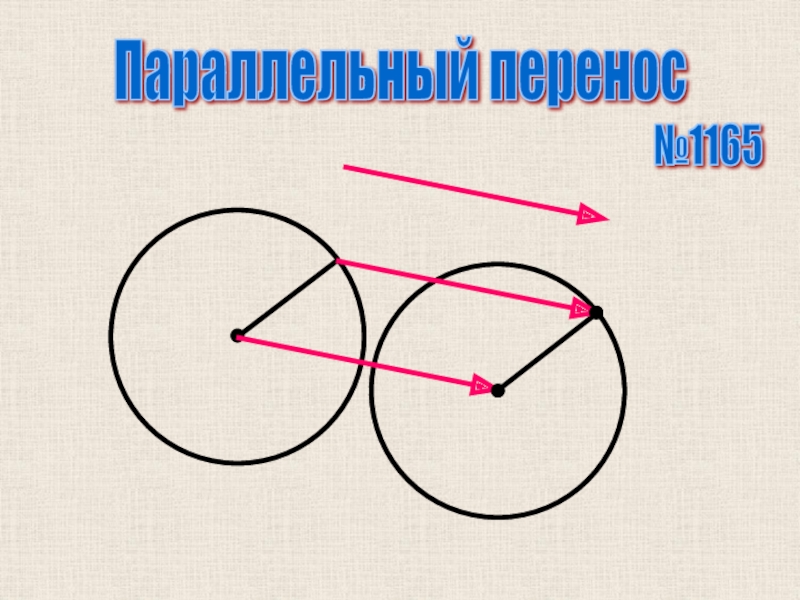
3. Параллельный перенос №1165
4. Параллельный перенос №1165
5. Параллельный перенос №1165
6. 1. Не обладает центром
7. 2. Не имеет оси симметрии фигура, изображённая на рисунке: А Б В Г
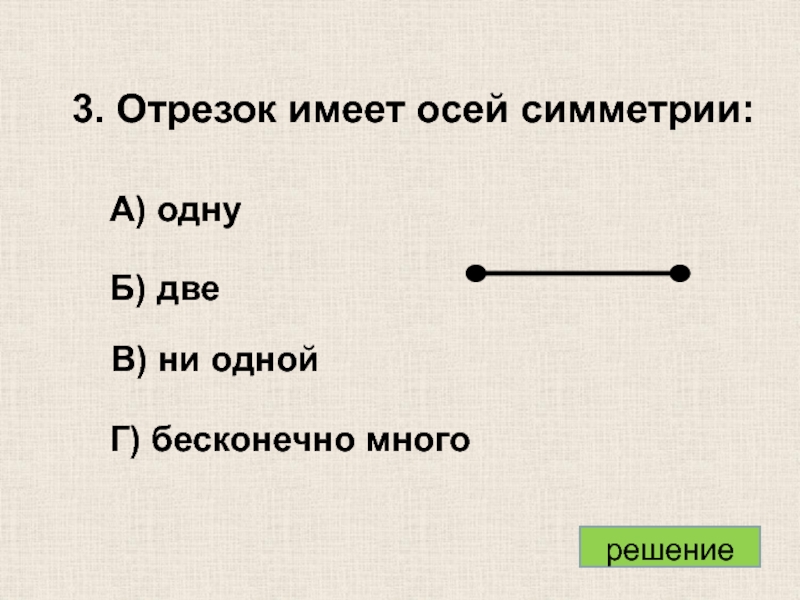
8. 3. Отрезок имеет осей симметрии: Б) две
9. 4. Центр симметрии имеет: А) параллелограмм; Б) равносторонний треугольник; В) трапеция; Г) правильный пятиугольник.
10. А) D; Б)
11. А) параллельную ей прямую; Б) перпендикулярную
12. А) x= -5; y=- 4; Б)
13. 8. При движении ромб отображается
14. изучение нового Отметим на плоскости точку
15. О α
16. Точка О называется центром поворота, α –
17. O М М1 М2
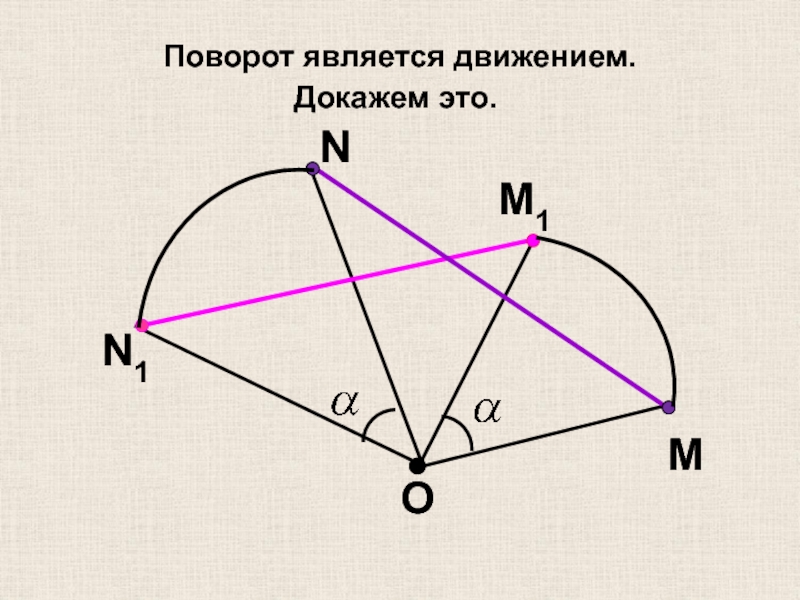
18. Поворот является движением. Докажем это.
19. Дано: ; N→
20. O M M1
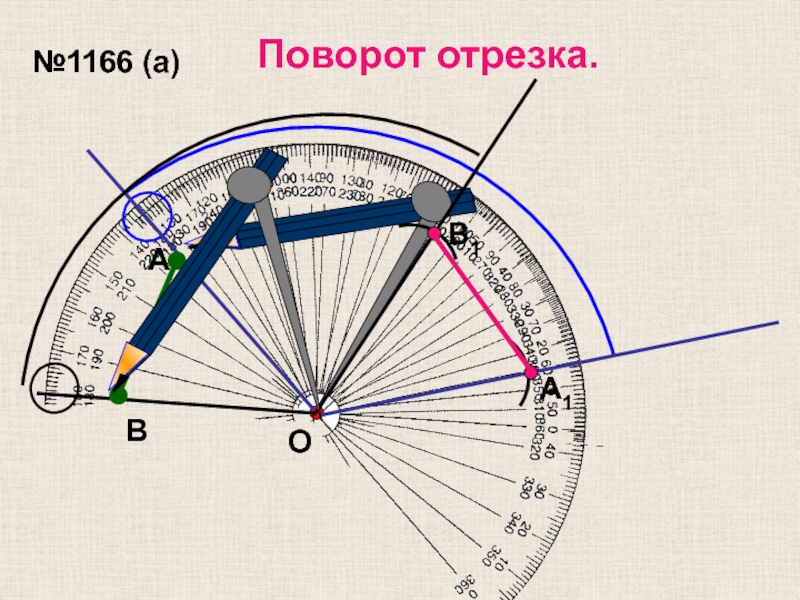
21. №1166 (а) А В О А1 В1 Поворот отрезка.
22. Задание. Построить фигуру, которая получится
23. A B O Задание. Построить фигуру, в
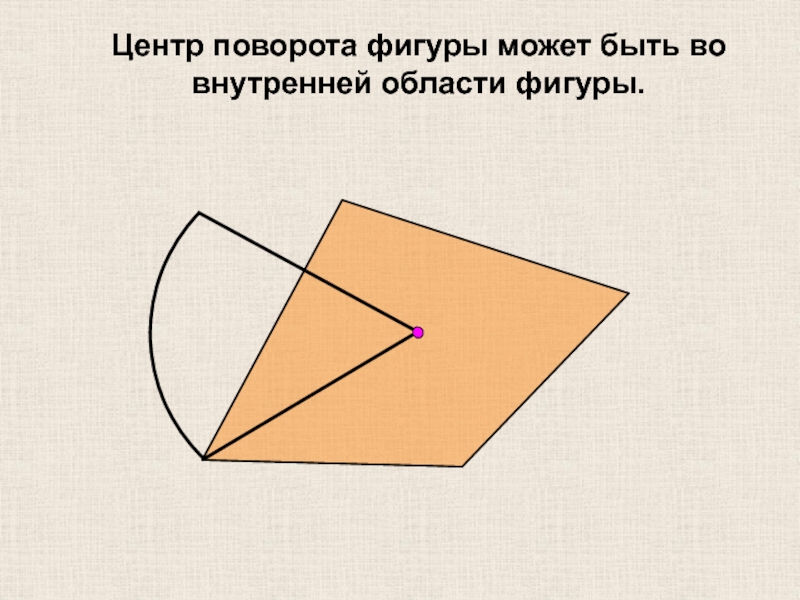
24. Центр поворота фигуры может быть во внутренней области фигуры.
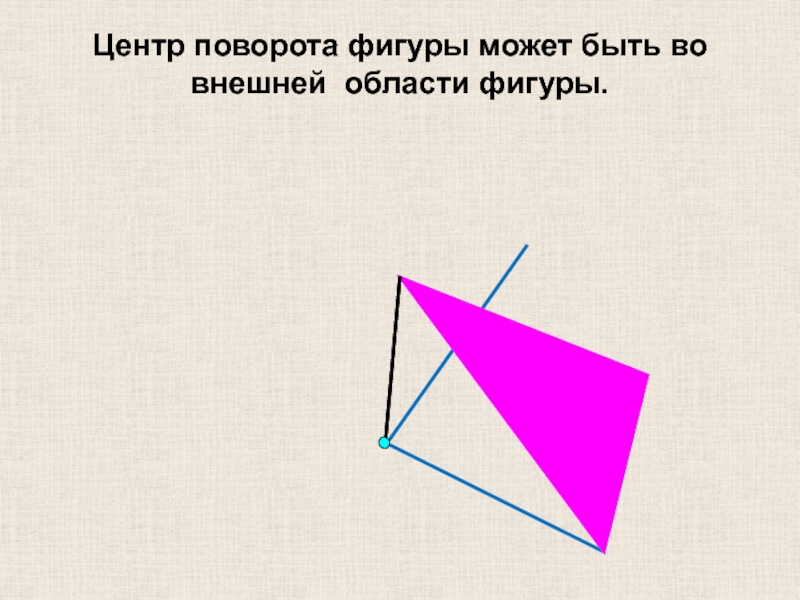
25. Центр поворота фигуры может быть во внешней области фигуры.
26. а) поворот; б) параллельный перенос; в) симметрия
27. 2. Определите по рисунку вид движения. а)
28. 3. Определите по рисунку вид движения. а)
29. 4. Определите по рисунку вид
30. 5. Определите по рисунку вид движения. а)

«Без движения — жизнь только летаргический сон». Жан Жак Руссо

Главная
Математика
Поворот. Параллельный перенос

Слайд 1Презентация к уроку в 9 классе
по теме:
«Поворот.»

Слайд 2«Без движения — жизнь только летаргический сон».
Жан Жак Руссо

Слайд 3Параллельный перенос

№1165

Слайд 4

Параллельный перенос

№1165

Слайд 5Параллельный перенос

№1165

Слайд 6
1. Не обладает центром симметрии фигура, изображенная
на рисунке

под буквой:

повторение

Слайд 72. Не имеет оси симметрии фигура,
изображённая на рисунке:
А
Б
В
Г

Слайд 83. Отрезок имеет осей симметрии:
Б) две
А) одну
В) ни одной
Г) бесконечно много

Слайд 94. Центр симметрии имеет:
А) параллелограмм;
Б) равносторонний треугольник;
В) трапеция;
Г) правильный пятиугольник.

Слайд 10А) D;
Б) C;
В) B;
Г) точку,

лежащую вне
параллелограмма ABCD;

5. ABCD – параллелограмм. При параллельном переносе на вектор CB точка A перейдёт в точку:

Слайд 11А) параллельную ей прямую;
Б) перпендикулярную ей прямую;
В) себя;
Г)

отрезок.

6. При осевой симметрии прямая, проходящая через ось симметрии будет отображаться на:

Слайд 12А) x= -5; y=- 4;
Б) x= 5; y=- 4;
В)

x= 5; y= 4;

Г) x= 4; y= -5;

7. Точка A имеет координаты: x= - 5; y= 4. Тогда точка C, симметричная точке A относительно
оси x, будет иметь координаты:

Слайд 138. При движении ромб
отображается на:
А) параллелограмм;
Б) квадрат;
В) произвольный четырёхугольник;
Г)

ромб.

Слайд 14изучение нового
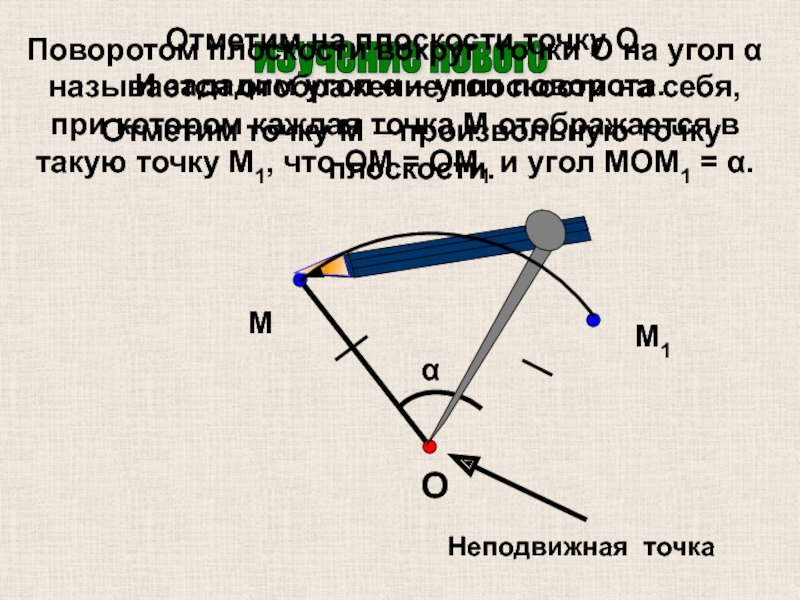
Отметим на плоскости точку О.
О
И зададим угол α

– угол поворота.

Неподвижная точка

Отметим точку M – произвольную точку плоскости.

Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка M отображается в такую точку M1, что OM = OM1 и угол MOM1 = α.

Слайд 15
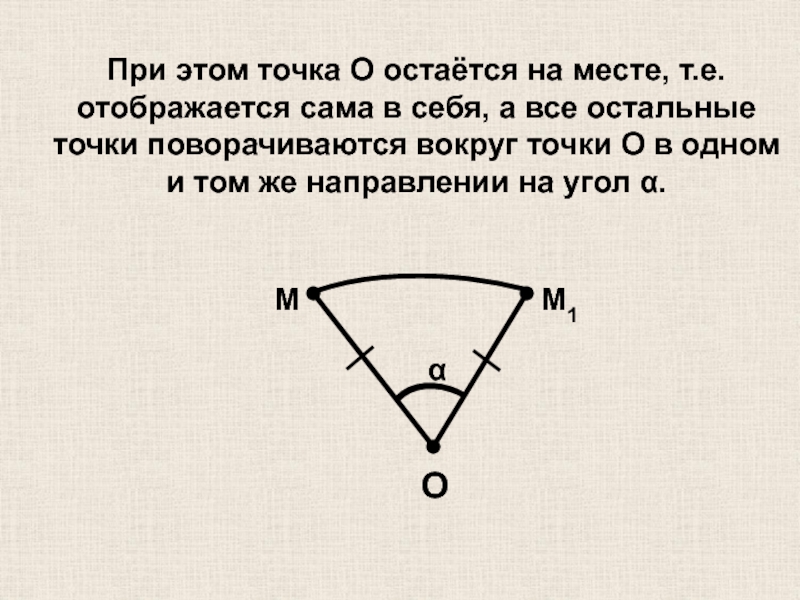
О

α

M
M1
При этом точка O остаётся на месте, т.е. отображается сама в

себя, а все остальные точки поворачиваются вокруг точки O в одном и том же направлении на угол α.

Слайд 16Точка О называется центром поворота,
α – угол поворота.

Обозначается .

Центр поворота

Слайд 17O

М
М1
М2

Если поворот выполняется по часовой стрелке, то угол поворота α считается

отрицательным.

Если поворот выполняется против часовой стрелки, то угол поворота – положительный.

Слайд 18 Поворот является движением. Докажем это.

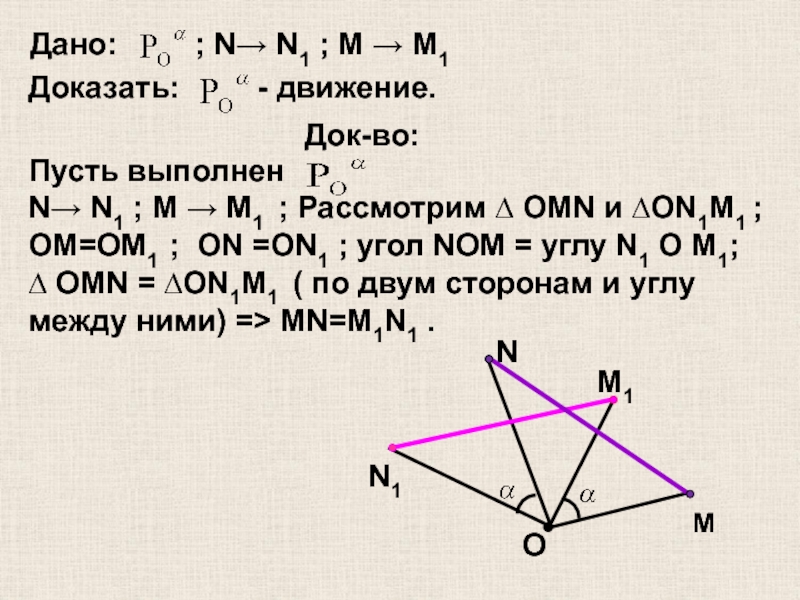
Слайд 19Дано: ; N→ N1 ; M →

М1

Доказать: - движение.

Док-во:

Пусть выполнен
N→ N1 ; M → М1 ; Рассмотрим ∆ OMN и ∆ON1М1 ;
OM=OМ1 ; ON =ON1 ; угол NOM = углу N1 O М1;
∆ OMN = ∆ON1М1 ( по двум сторонам и углу между ними) => MN=М1N1 .

Слайд 20

O
M

M1
Задание. Построить точку M1, которая получается из точки M поворотом

на угол 600.

Слайд 21
№1166 (а)

А
В

О

А1

В1
Поворот отрезка.

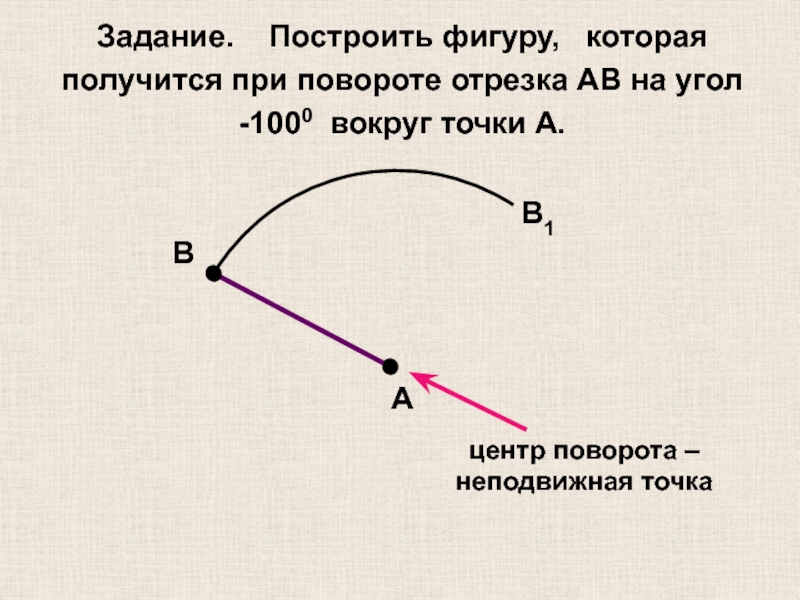
Слайд 22Задание. Построить фигуру, которая получится при повороте отрезка AB

на угол
-1000 вокруг точки А.

центр поворота – неподвижная точка

Слайд 23A
B
O
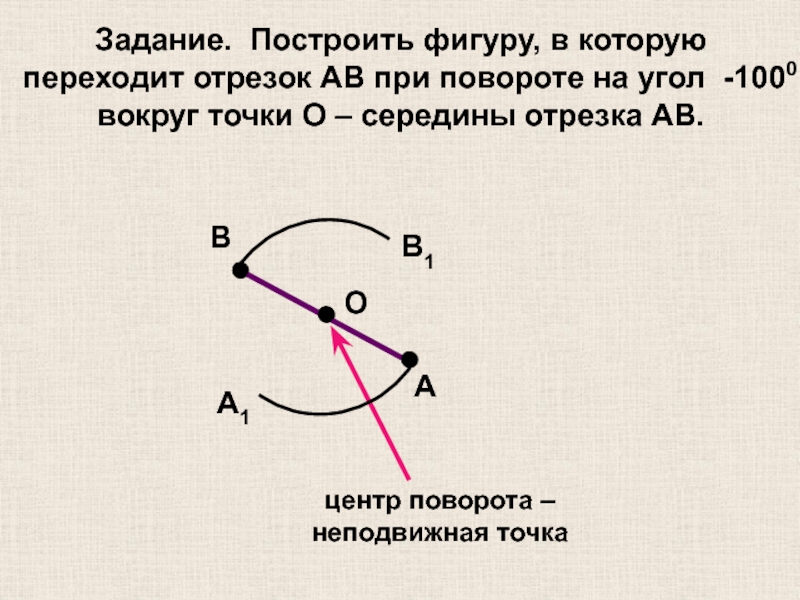
Задание. Построить фигуру, в которую переходит отрезок AB при повороте на

угол -1000
вокруг точки О – середины отрезка AB.

центр поворота – неподвижная точка

Слайд 24Центр поворота фигуры может быть во внутренней области фигуры.

Слайд 25Центр поворота фигуры может быть во внешней области фигуры.

Слайд 26а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не

является движением;

1. Определите по рисунку вид движения.

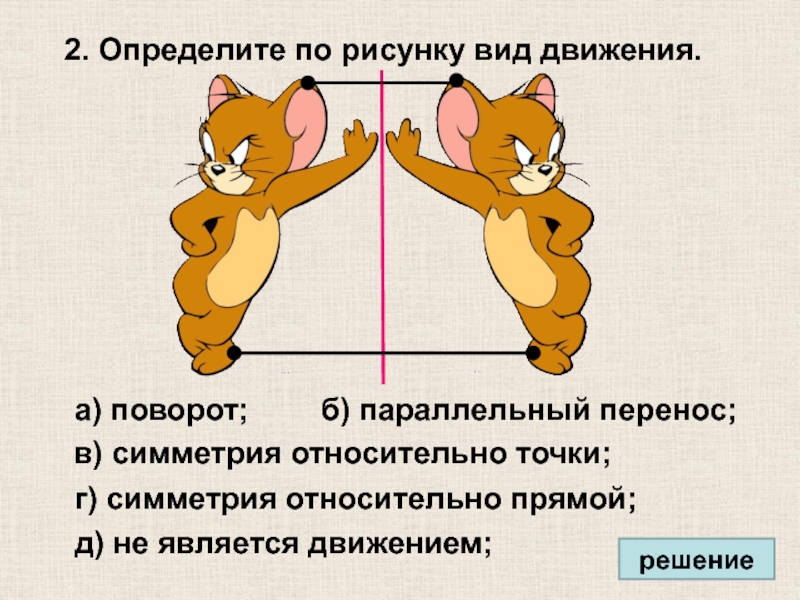
Слайд 272. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия

относительно прямой;

д) не является движением;

б) параллельный перенос;

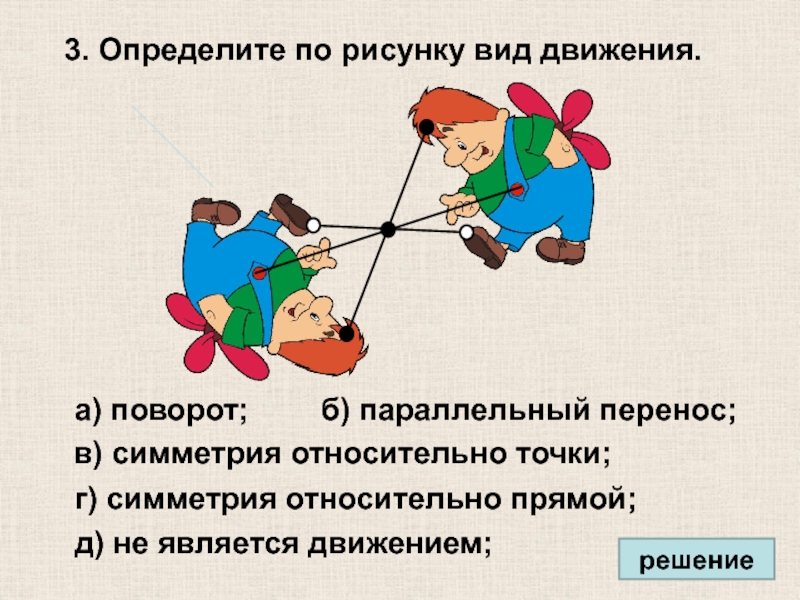
Слайд 283. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия

относительно прямой;

д) не является движением;

б) параллельный перенос;

Слайд 29

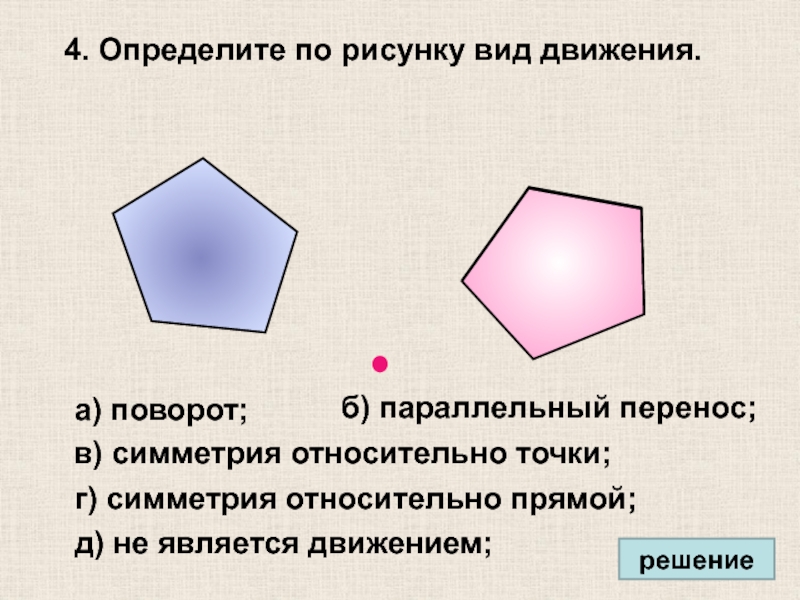
4. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия относительно

точки;

г) симметрия относительно прямой;

д) не является движением;

Слайд 305. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия

относительно прямой;

д) не является движением;

б) параллельный перенос;

Скачать презентацию

Поворот. Параллельный перенос презентация

Содержание

Слайд 1Презентация к уроку в 9 классе
по теме:
«Поворот.»

Слайд 2«Без движения — жизнь только летаргический сон».
Жан Жак Руссо

Слайд 3Параллельный перенос

№1165

Слайд 4

Параллельный перенос

№1165

Слайд 5Параллельный перенос

№1165

Слайд 6
1. Не обладает центром симметрии фигура, изображенная
на рисунке

Слайд 72. Не имеет оси симметрии фигура,
изображённая на рисунке:
А
Б
В
Г

Слайд 83. Отрезок имеет осей симметрии:
Б) две
А) одну
В) ни одной
Г) бесконечно много

Слайд 94. Центр симметрии имеет:
А) параллелограмм;
Б) равносторонний треугольник;
В) трапеция;
Г) правильный пятиугольник.

Слайд 10А) D;
Б) C;
В) B;
Г) точку,

Слайд 11А) параллельную ей прямую;
Б) перпендикулярную ей прямую;
В) себя;
Г)

Слайд 12А) x= -5; y=- 4;
Б) x= 5; y=- 4;
В)

Слайд 138. При движении ромб
отображается на:
А) параллелограмм;
Б) квадрат;
В) произвольный четырёхугольник;
Г)

Слайд 14изучение нового
Отметим на плоскости точку О.
О
И зададим угол α

Слайд 15
О

α

M
M1
При этом точка O остаётся на месте, т.е. отображается сама в

Слайд 16Точка О называется центром поворота,
α – угол поворота.

Слайд 17O

М
М1
М2

Если поворот выполняется по часовой стрелке, то угол поворота α считается

Слайд 18 Поворот является движением. Докажем это.

Слайд 19Дано: ; N→ N1 ; M →

Слайд 20

O
M

M1
Задание. Построить точку M1, которая получается из точки M поворотом

Слайд 21
№1166 (а)

А
В

О

А1

В1
Поворот отрезка.

Слайд 22Задание. Построить фигуру, которая получится при повороте отрезка AB

Слайд 23A
B
O
Задание. Построить фигуру, в которую переходит отрезок AB при повороте на

Слайд 24Центр поворота фигуры может быть во внутренней области фигуры.

Слайд 25Центр поворота фигуры может быть во внешней области фигуры.

Слайд 26а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не

Слайд 272. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия

Слайд 283. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия

Слайд 29

4. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия относительно

Слайд 305. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия

Обратная связь

Что такое ThePresentation.ru?

Поворот. Параллельный перенос презентация

Содержание

Слайд 1Презентация к уроку в 9 классе по теме: «Поворот.»

Слайд 2«Без движения — жизнь только летаргический сон».Жан Жак Руссо

Слайд 3Параллельный перенос №1165

Слайд 4Параллельный перенос №1165

Слайд 5Параллельный перенос №1165

Слайд 6 1. Не обладает центром симметрии фигура, изображенная на рисунке

Слайд 72. Не имеет оси симметрии фигура,изображённая на рисунке:АБВГ

Слайд 83. Отрезок имеет осей симметрии:Б) двеА) однуВ) ни однойГ) бесконечно много

Слайд 94. Центр симметрии имеет:А) параллелограмм;Б) равносторонний треугольник;В) трапеция;Г) правильный пятиугольник.

Слайд 10А) D;Б) C;В) B;Г) точку,

Слайд 11А) параллельную ей прямую;Б) перпендикулярную ей прямую;В) себя;Г)

Слайд 12А) x= -5; y=- 4;Б) x= 5; y=- 4;В)

Слайд 138. При движении ромб отображается на:А) параллелограмм;Б) квадрат;В) произвольный четырёхугольник;Г)

Слайд 14изучение нового Отметим на плоскости точку О. ОИ зададим угол α

Слайд 15ОαMM1При этом точка O остаётся на месте, т.е. отображается сама в

Слайд 16Точка О называется центром поворота,α – угол поворота.

Слайд 17OММ1М2Если поворот выполняется по часовой стрелке, то угол поворота α считается

Слайд 18 Поворот является движением. Докажем это.

Слайд 19Дано: ; N→ N1 ; M →

Слайд 20OMM1Задание. Построить точку M1, которая получается из точки M поворотом

Слайд 21№1166 (а)АВОА1В1Поворот отрезка.

Слайд 22Задание. Построить фигуру, которая получится при повороте отрезка AB

Слайд 23ABOЗадание. Построить фигуру, в которую переходит отрезок AB при повороте на

Слайд 24Центр поворота фигуры может быть во внутренней области фигуры.

Слайд 25Центр поворота фигуры может быть во внешней области фигуры.

Слайд 26а) поворот;б) параллельный перенос;в) симметрия относительно точки;г) симметрия относительно прямой;д) не

Слайд 272. Определите по рисунку вид движения.а) поворот;в) симметрия относительно точки;г) симметрия

Слайд 283. Определите по рисунку вид движения.а) поворот;в) симметрия относительно точки;г) симметрия

Слайд 294. Определите по рисунку вид движения.а) поворот;б) параллельный перенос;в) симметрия относительно

Слайд 305. Определите по рисунку вид движения.а) поворот;в) симметрия относительно точки;г) симметрия

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Презентация к уроку в 9 классе
по теме:
«Поворот.»

Слайд 2«Без движения — жизнь только летаргический сон».
Жан Жак Руссо

Слайд 3Параллельный перенос

№1165

Слайд 4

Параллельный перенос

№1165

Слайд 5Параллельный перенос

№1165

Слайд 6
1. Не обладает центром симметрии фигура, изображенная
на рисунке

Слайд 72. Не имеет оси симметрии фигура,
изображённая на рисунке:
А
Б
В
Г

Слайд 83. Отрезок имеет осей симметрии:
Б) две
А) одну
В) ни одной
Г) бесконечно много

Слайд 94. Центр симметрии имеет:
А) параллелограмм;
Б) равносторонний треугольник;
В) трапеция;
Г) правильный пятиугольник.

Слайд 10А) D;
Б) C;
В) B;
Г) точку,

Слайд 11А) параллельную ей прямую;
Б) перпендикулярную ей прямую;
В) себя;
Г)

Слайд 12А) x= -5; y=- 4;
Б) x= 5; y=- 4;
В)

Слайд 138. При движении ромб
отображается на:
А) параллелограмм;
Б) квадрат;
В) произвольный четырёхугольник;
Г)

Слайд 14изучение нового
Отметим на плоскости точку О.
О
И зададим угол α

Слайд 15
О

α

M
M1
При этом точка O остаётся на месте, т.е. отображается сама в

Слайд 16Точка О называется центром поворота,
α – угол поворота.

Слайд 17O

М
М1
М2

Если поворот выполняется по часовой стрелке, то угол поворота α считается

Слайд 20

O
M

M1
Задание. Построить точку M1, которая получается из точки M поворотом

Слайд 21
№1166 (а)

А
В

О

А1

В1
Поворот отрезка.

Слайд 23A
B
O
Задание. Построить фигуру, в которую переходит отрезок AB при повороте на

Слайд 26а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не

Слайд 272. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия

Слайд 283. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия

Слайд 29

4. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия относительно

Слайд 305. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г) симметрия