- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности второго порядка. Однополостный и двуполостный гиперболоид презентация
Содержание
- 1. Поверхности второго порядка. Однополостный и двуполостный гиперболоид
- 2. Общее уравнение поверхности второго порядка
- 3. Матричный вид уравнения поверхности второго порядка
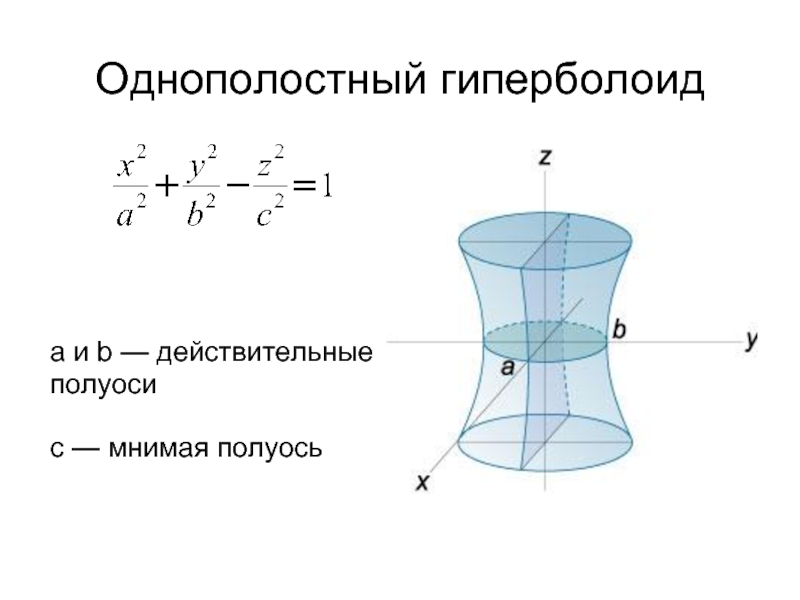
- 4. Однополостный гиперболоид a и b — действительные полуоси c — мнимая полуось
- 5. Свойства однополостного гиперболоида: 1. Однополостный гиперболоид -
- 6. 3. В сечении однополостного гиперболоида плоскостью, ортогональной
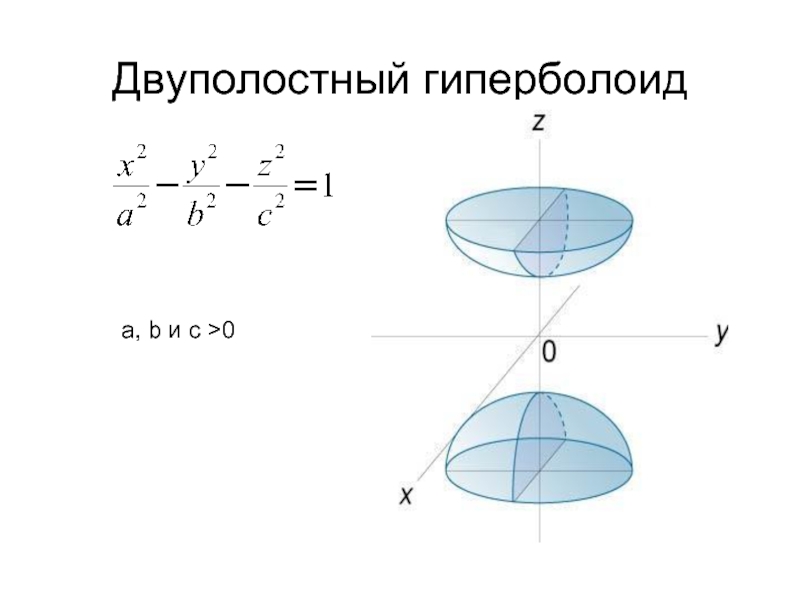
- 7. Двуполостный гиперболоид a, b и c >0
- 8. Свойства двуполостного гиперболоида: Двуполостный гиперболоид -
- 9. Сделал презентацию Халилов Илья Викторович ИС 151
Слайд 2Общее уравнение поверхности второго порядка
x, y, z − координаты точек
поверхности
− действительные числа.
− действительные числа.
Слайд 5Свойства однополостного гиперболоида:
1. Однополостный гиперболоид - неограниченная поверхность, поскольку из его
канонического уравнения следует, что
2. Однополостный гиперболоид обладает:
- центральной симметрией относительно начала координат;
- осевой симметрией относительно всех координатных осей;
- плоскостной симметрией относительно всех координатных плоскостей.
2. Однополостный гиперболоид обладает:
- центральной симметрией относительно начала координат;
- осевой симметрией относительно всех координатных осей;
- плоскостной симметрией относительно всех координатных плоскостей.
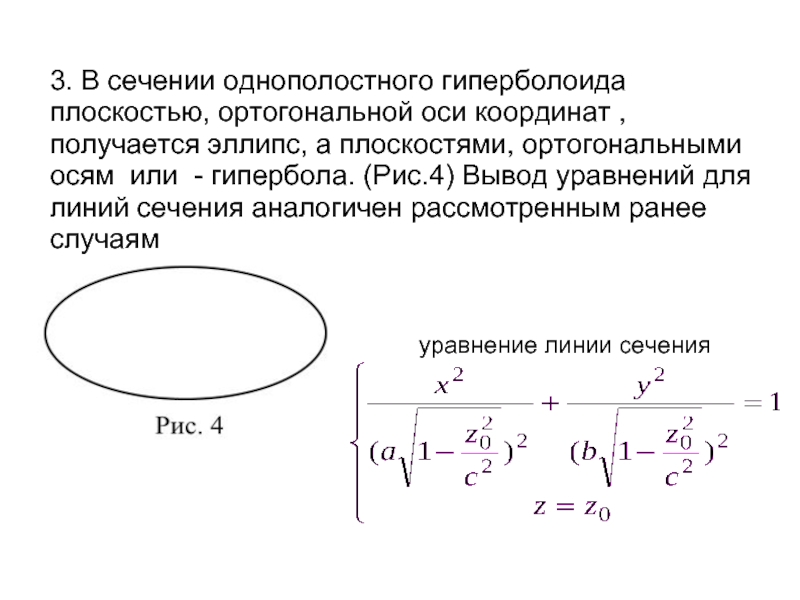
Слайд 63. В сечении однополостного гиперболоида плоскостью, ортогональной оси координат , получается
эллипс, а плоскостями, ортогональными осям или - гипербола. (Рис.4) Вывод уравнений для линий сечения аналогичен рассмотренным ранее случаям
уравнение линии сечения
Слайд 8Свойства двуполостного гиперболоида:
Двуполостный гиперболоид - неограниченная поверхность, поскольку из его
канонического уравнения следует, что и не ограничен сверху
Двуполостный гиперболоид обладает:
- центральной симметрией относительно начала координат;
- осевой симметрией относительно всех координатных осей;
- В сечении двуполостного гиперболоида плоскостью, ортогональной оси координат Ox, при |x|>a получается эллипс, а плоскостями, ортогональными осям Oz или Oy - гипербола.
Двуполостный гиперболоид обладает:
- центральной симметрией относительно начала координат;
- осевой симметрией относительно всех координатных осей;
- В сечении двуполостного гиперболоида плоскостью, ортогональной оси координат Ox, при |x|>a получается эллипс, а плоскостями, ортогональными осям Oz или Oy - гипербола.