- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности. (Лекция 5) презентация
Содержание
- 1. Поверхности. (Лекция 5)
- 2. Следует рассматривать поверхность как
- 3. Каркас поверхности – множество линий, определяющих поверхность.
- 4. Основой классификации поверхностей могут служить их определители
- 5. Классификация поверхностей По виду образующей:
- 6. Линейчатые развёртываемые поверхности Цилиндрические поверхности
- 7. Призматические поверхности Ф(a, m, s)
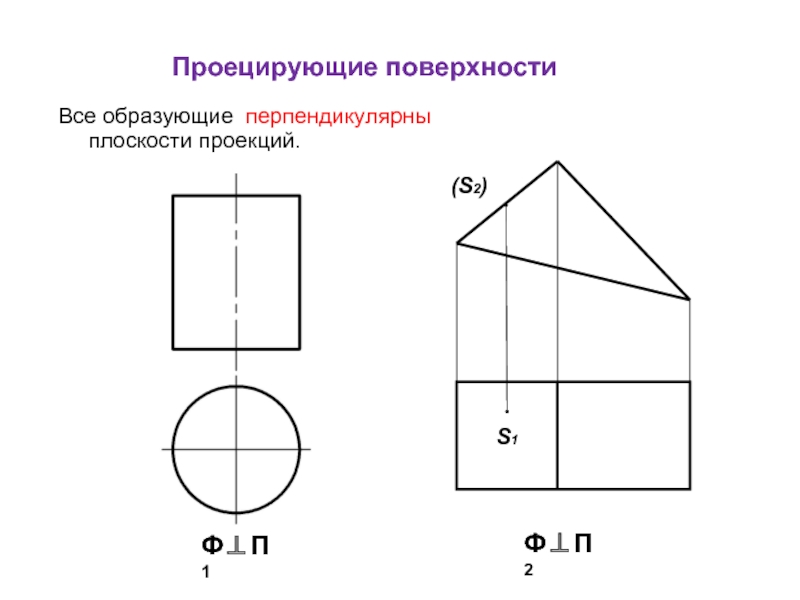
- 8. Проецирующие поверхности Все образующие перпендикулярны плоскости проекций. (S2) S1 Ф⊥П 1 Ф⊥П 2
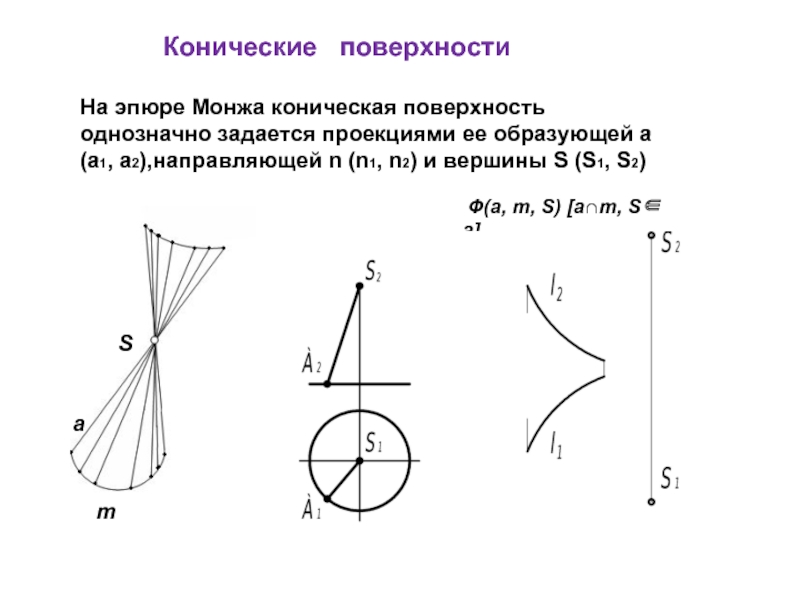
- 9. На эпюре Монжа коническая поверхность однозначно задается
- 10. Пирамидальные
- 11. Поверхности вращения общего вида Ф(а, i)
- 13. П В, образованные вращением линии Прямой круговой
- 14. i Ф(а, i) a
- 15. Ф(а, i) a ∩ i = s
- 16. П В, образованные вращением окружности Сфера Тор
- 17. Сфера x2 + y2 + z2 =
- 18. Тор закрытый (x2 + y2 + z2
- 19. Тор открытый (x2 + y2 + z2
- 20. Эллипсоид вращения a2(x2 + y2) + b2z2
- 21. Ф(а, i) Гиперболоид вращения b2z2 –
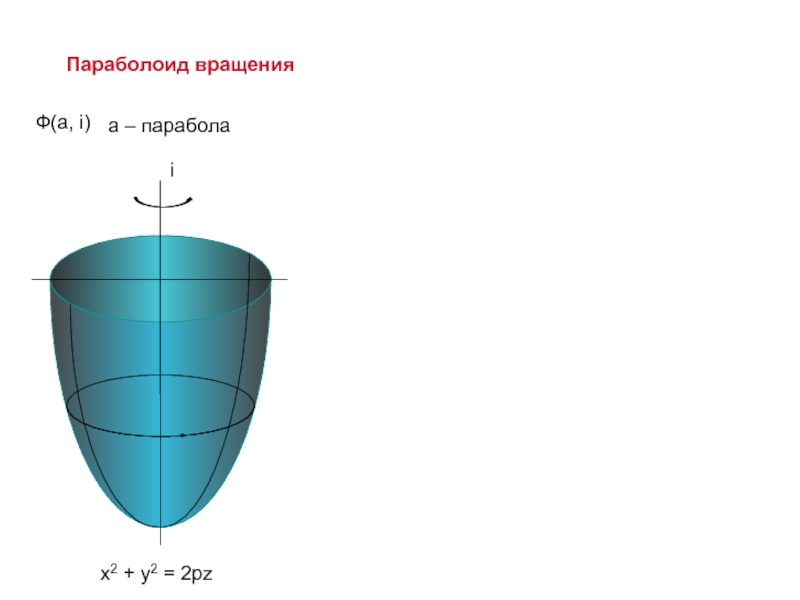
- 22. i Параболоид вращения x2 +
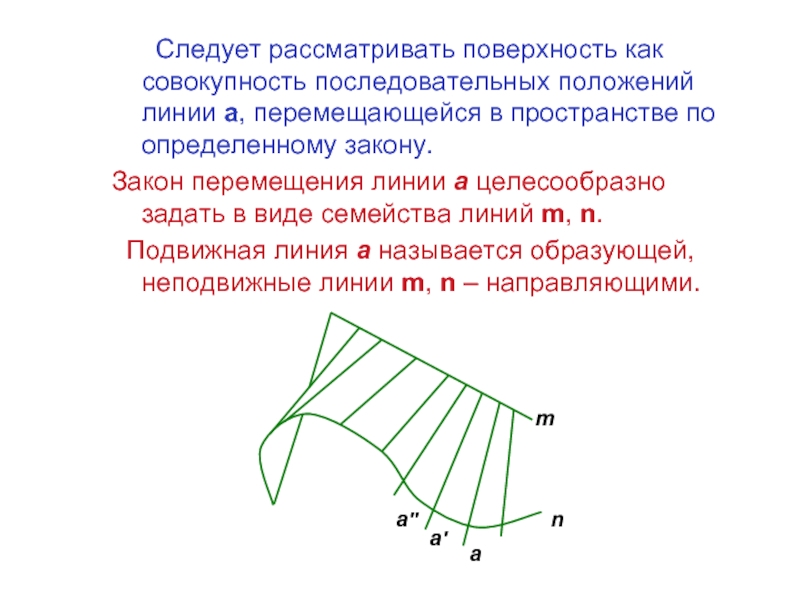
Слайд 2 Следует рассматривать поверхность как совокупность последовательных положений линии
Закон перемещения линии а целесообразно задать в виде семейства линий m, n.
Подвижная линия а называется образующей, неподвижные линии m, n – направляющими.
m
n
a''
a
a'
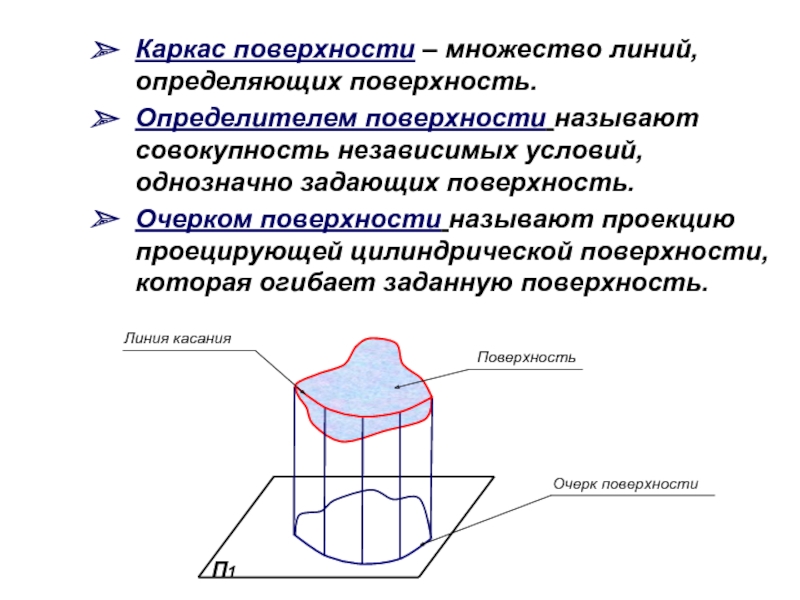
Слайд 3Каркас поверхности – множество линий, определяющих поверхность.
Определителем поверхности называют совокупность
Очерком поверхности называют проекцию проецирующей цилиндрической поверхности, которая огибает заданную поверхность.
П1
Очерк поверхности
Поверхность
Линия касания
Слайд 4Основой классификации поверхностей могут
служить их определители или геометрические
особенности, связанные с кинематическим
способом
Важными признаками формообразования поверхностей являются:
Вид образующей;
Постоянство образующей;
Закон перемещения образующей;
Развёртываемость куска поверхности.
Слайд 5Классификация поверхностей
По виду образующей:
Линейчатые
Нелинейчатые
По постоянству образующей:
С постоянной образующей
С переменной образующей
По закону движения образующей:
Кинематические поверхности
Поверхности вращения
Винтовые поверхности
По развёртываемости:
Развёртываемые
Не развёртываемые
Слайд 6Линейчатые развёртываемые поверхности
Цилиндрические поверхности
Ф(a, m, s) [a ∩
m-кривая направляющая
s-направляющий вектор
Если m-окружность и m⊥a, то поверхностью будет прямой круговой цилиндр.
m
a
s
a'
a''
a'''
a''''
Слайд 7Призматические поверхности
Ф(a, m, s) [a ∩ m, a II s]
s-направляющий вектор
a
s
m
a'
a'''
a''
Слайд 9На эпюре Монжа коническая поверхность однозначно задается проекциями ее образующей a
S
m
a
Конические поверхности
Ф(a, m, S) [a∩m, S∈ a]
Слайд 11
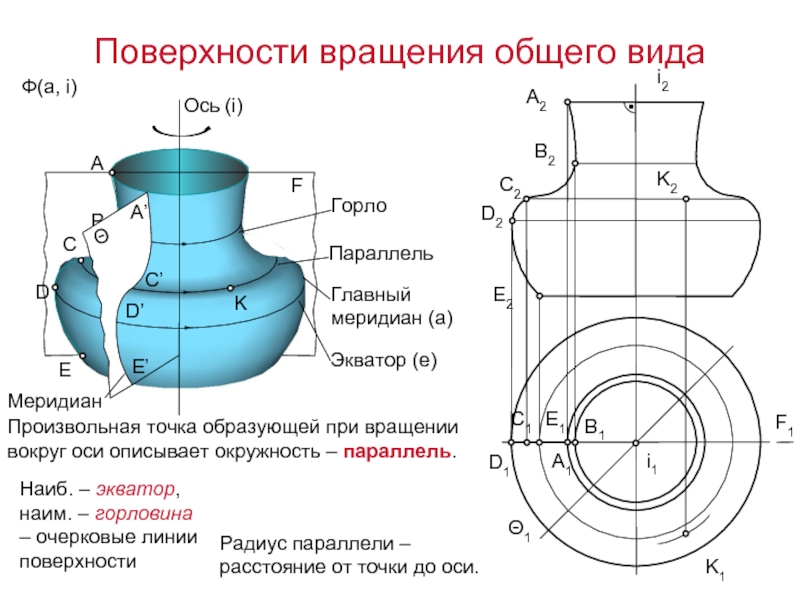
Поверхности вращения общего вида
Ф(а, i)
F1
Θ1
K1
K2
i2
Ось (i)
Произвольная точка образующей при вращении вокруг
Радиус параллели – расстояние от точки до оси.
Наиб. – экватор, наим. – горловина – очерковые линии поверхности
i1
A2
B2
C2
D2
E2
E1
C1
D1
B1
A1
A
C
D
E
B
K
Параллель
F
Горло
Главный меридиан (а)
Экватор (е)
Меридиан
B’
C’
D’
E’
Θ
A’
Слайд 12
F1
Θ1
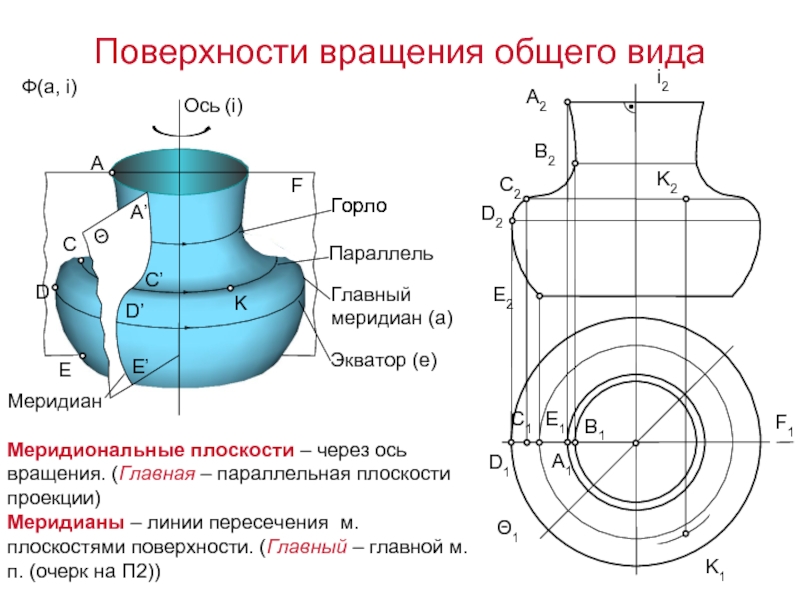
Меридиональные плоскости – через ось вращения. (Главная – параллельная плоскости проекции)
Меридианы
K1
K2
A2
B2
C2
D2
E2
E1
C1
D1
B1
A1
i2
Ф(а, i)
Ось (i)
A
C
D
E
K
Параллель
F
Горло
B’
C’
D’
E’
Θ
A’
Горло
Главный меридиан (а)
Экватор (е)
Меридиан
Поверхности вращения общего вида
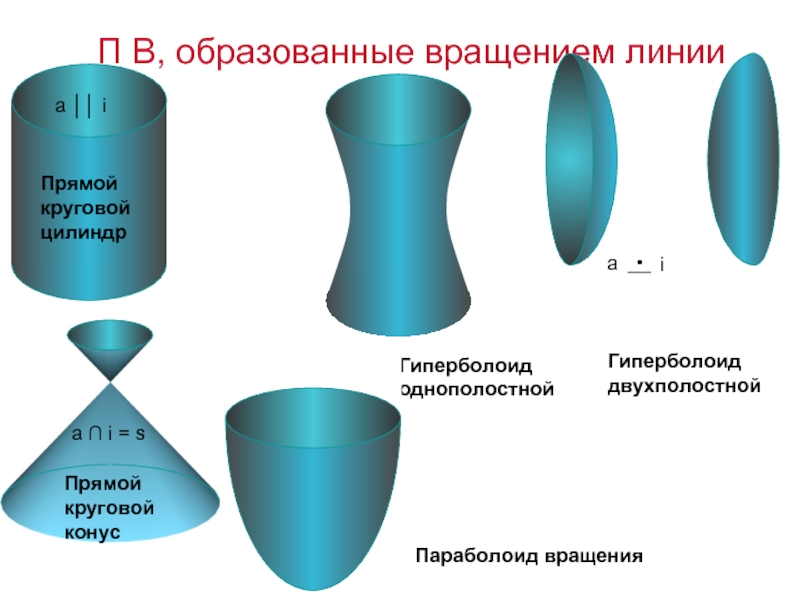
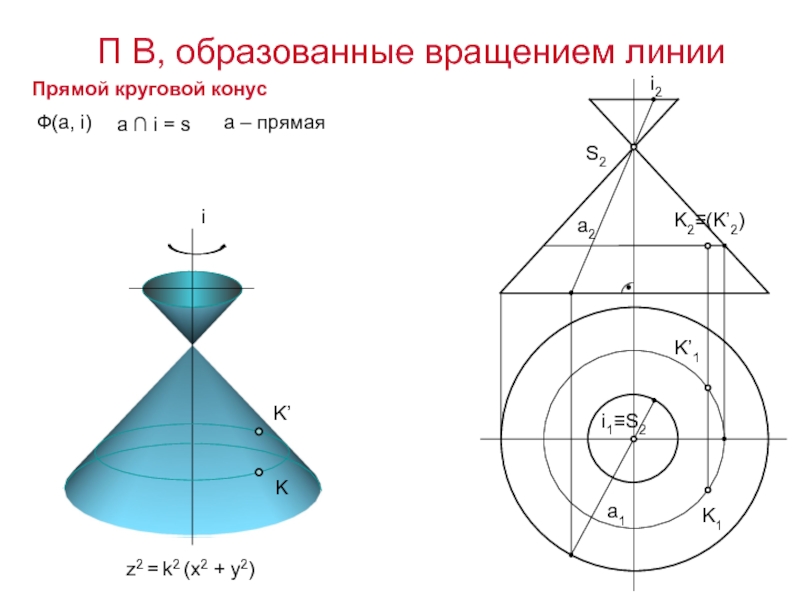
Слайд 13П В, образованные вращением линии
Прямой круговой конус
Гиперболоид однополостной
Параболоид вращения
Гиперболоид двухполостной
Прямой круговой
a ∩ i = s
a ││ i
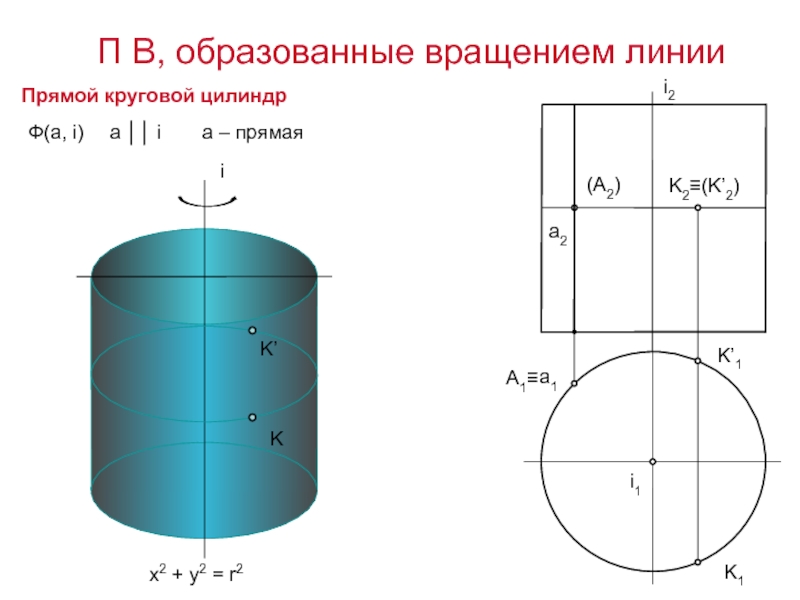
Слайд 14
i
Ф(а, i)
a ││ i
Прямой круговой цилиндр
x2 + y2 = r2
а –
K’1
i2
K2≡(K’2)
a2
(A2)
K1
i1
A1≡
П В, образованные вращением линии
a1
Слайд 15Ф(а, i)
a ∩ i = s
Прямой круговой конус
z2 = k2 (x2
а – прямая
K1
K’1
i2
K2≡(K’2)
a1
a2
i1≡S2
S2
i
П В, образованные вращением линии
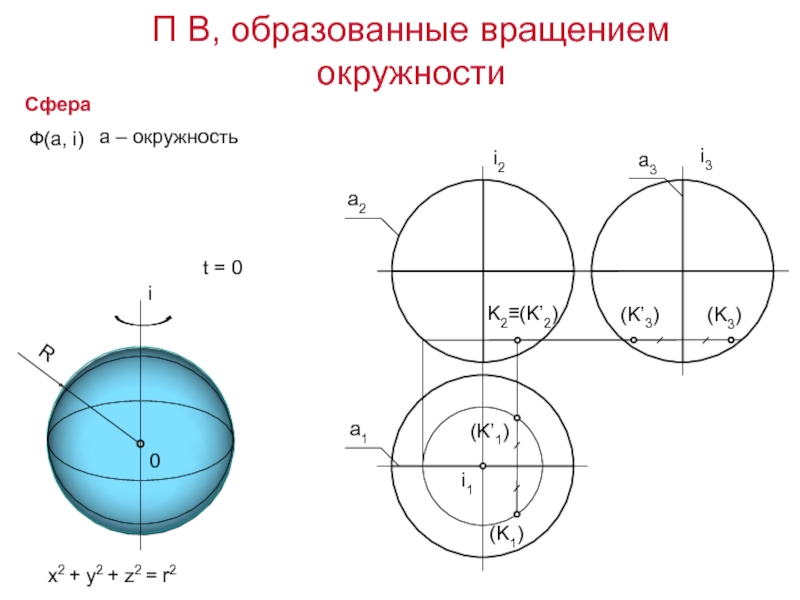
Слайд 17Сфера
x2 + y2 + z2 = r2
П В, образованные вращением окружности
Ф(а,
а – окружность
t = 0
i
i2
i1
(K1)
(K’1)
K2≡(K’2)
a1
i3
a3
a2
(K’3)
(K3)
0
R
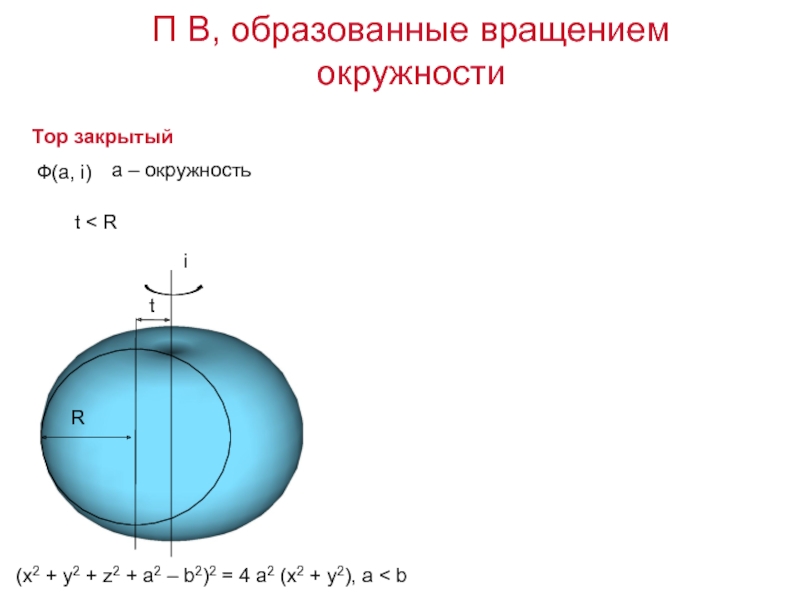
Слайд 18Тор закрытый
(x2 + y2 + z2 + a2 – b2)2 =
t < R
Ф(а, i)
а – окружность
П В, образованные вращением окружности
i
t
0
R
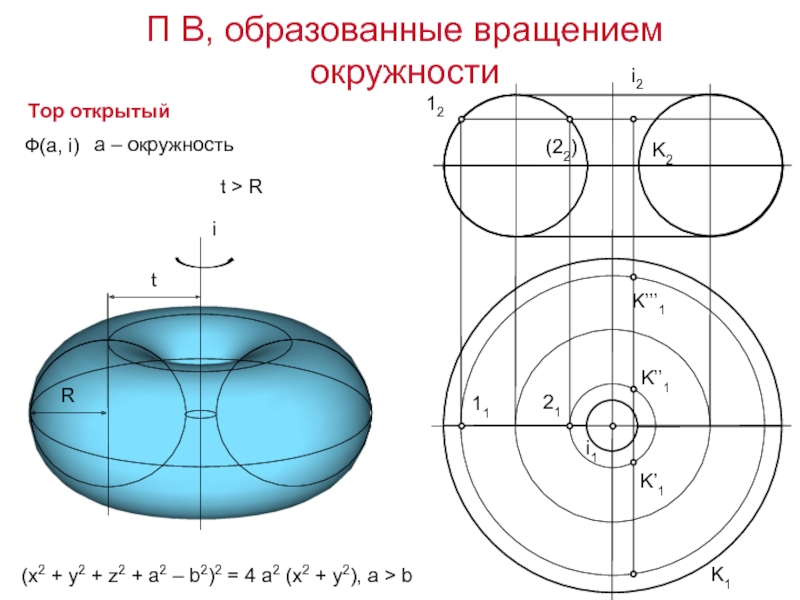
Слайд 19Тор открытый
(x2 + y2 + z2 + a2 – b2)2 =
Ф(а, i)
t > R
t
а – окружность
K’1
i2
K1
i1
K’’1
K’’’1
11
21
12
(22)
K2
П В, образованные вращением окружности
0
i
R
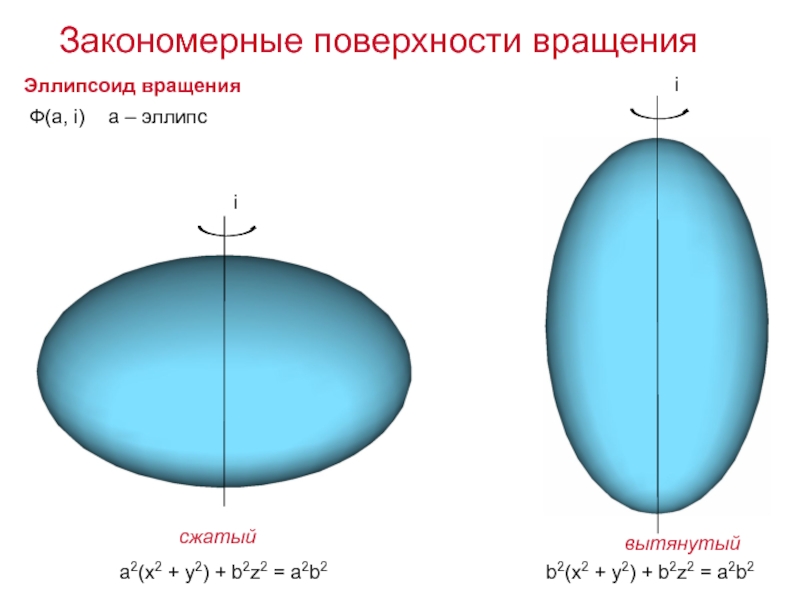
Слайд 20Эллипсоид вращения
a2(x2 + y2) + b2z2 = a2b2
сжатый
вытянутый
b2(x2 + y2) +
Закономерные поверхности вращения
Ф(а, i)
а – эллипс
i
i
Слайд 21
Ф(а, i)
Гиперболоид вращения
b2z2 – a2(x2 + y2) = a2b2
b2(x2 + y2)
двухполостной
i
а – гипербола
i
однополостной



![Линейчатые развёртываемые поверхности Цилиндрические поверхности Ф(a, m, s) [a ∩ m, a II s],](/img/tmb/2/165477/97e06aa1dc4e8d505f0b5f39b8b33338-800x.jpg)
![Призматические поверхности Ф(a, m, s) [a ∩ m, a II s] m-ломаная линия s-направляющий вектор asma'a'''a''](/img/tmb/2/165477/914dcdb35aabea7dffdabcbfa1a8a045-800x.jpg)
![Пирамидальные поверхности Sama'a''a'''Ф(a, m, S) [a∩m, S∈ a]](/img/tmb/2/165477/b0fd1b3c98dbc49eb4d171ba0d358867-800x.jpg)