- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение сечений многогранников методом следа презентация
Содержание
- 1. Построение сечений многогранников методом следа
- 2. Секущей плоскостью многогранника называется такая
- 3. Секущая плоскость пересекает грани многогранника по отрезкам,
- 4. Две плоскости пересекаются по прямой (эта
- 5. A B C D B1 C1
- 6. A B C D B1 C1
- 7. A B C D B1 C1
- 8. A B C D B1 C1
- 9. A B C D B1 C1
- 10. A B C D C1 D1
- 11. ПРИМЕР 2. M N K Построить
- 12. ПРИМЕР 3. Построить
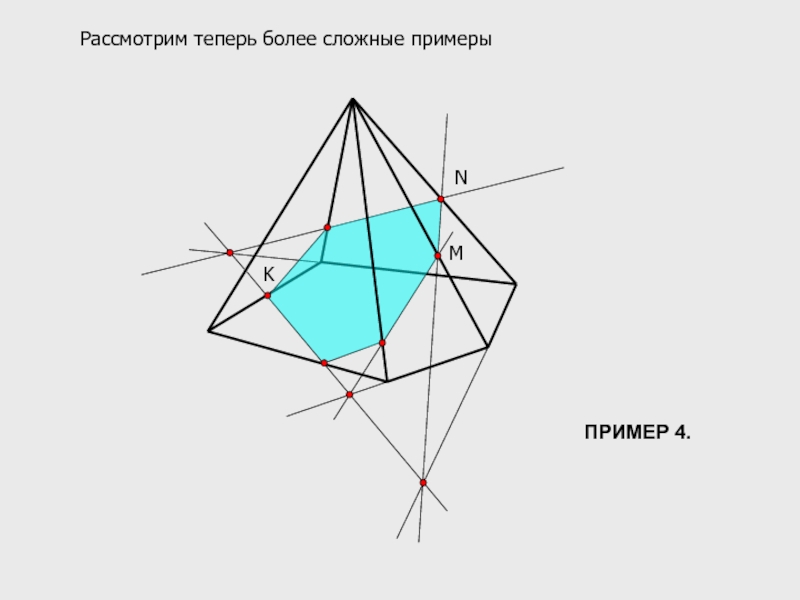
- 13. M N K Рассмотрим теперь более
- 14. M N K Помним о том, что
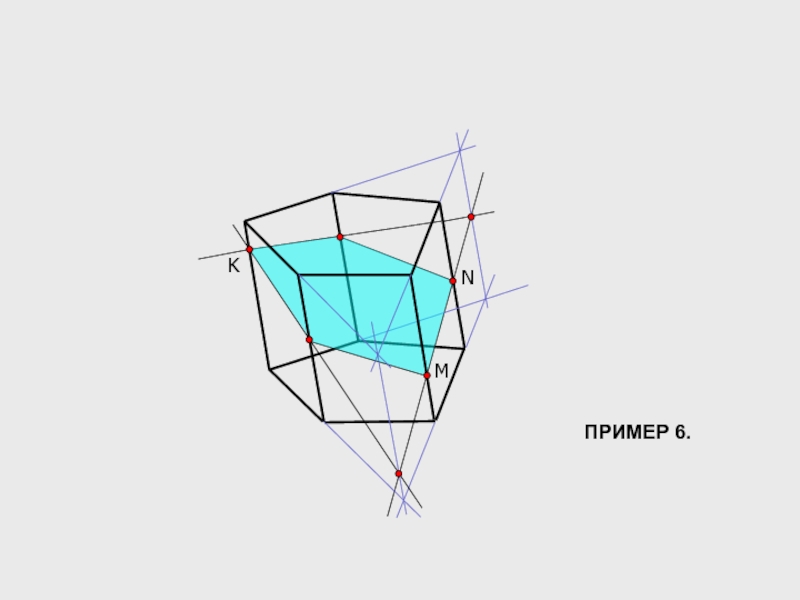
- 15. K M N ПРИМЕР 6.
- 16. Плоскость сечения может задаваться: 1) тремя
- 17. Заключение Данный метод построения сечений многогранников можно
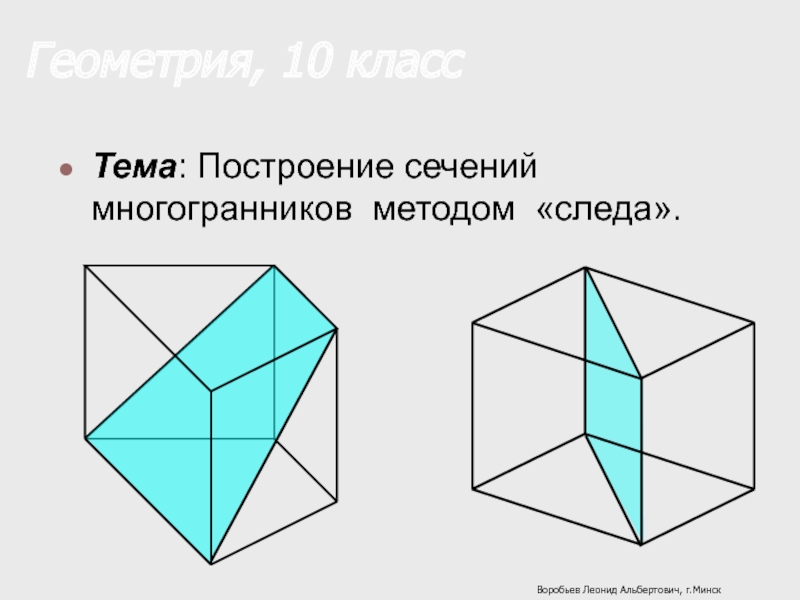
Слайд 1Геометрия, 10 класс
Тема: Построение сечений многогранников методом «следа».
Воробьев Леонид Альбертович, г.Минск
Слайд 2
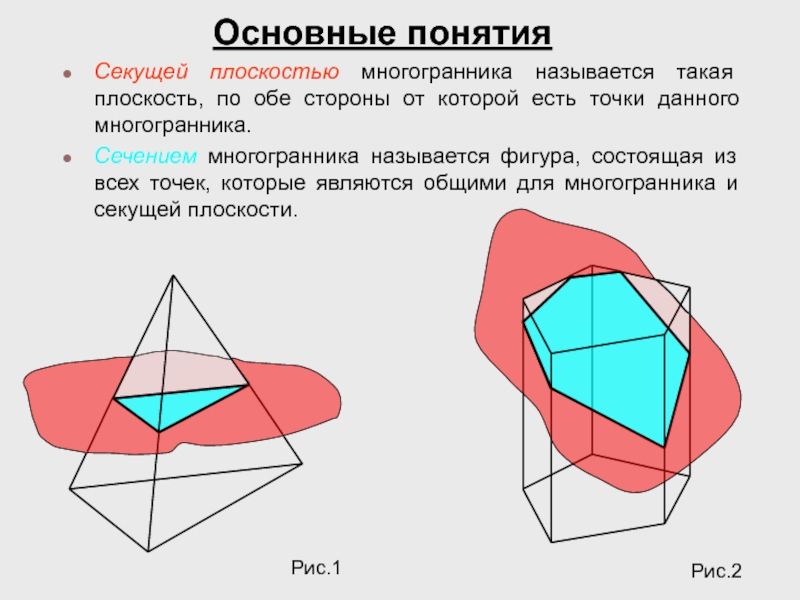
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой
есть точки данного многогранника.
Сечением многогранника называется фигура, состоящая из всех точек, которые являются общими для многогранника и секущей плоскости.
Сечением многогранника называется фигура, состоящая из всех точек, которые являются общими для многогранника и секущей плоскости.
Основные понятия
Рис.1
Рис.2
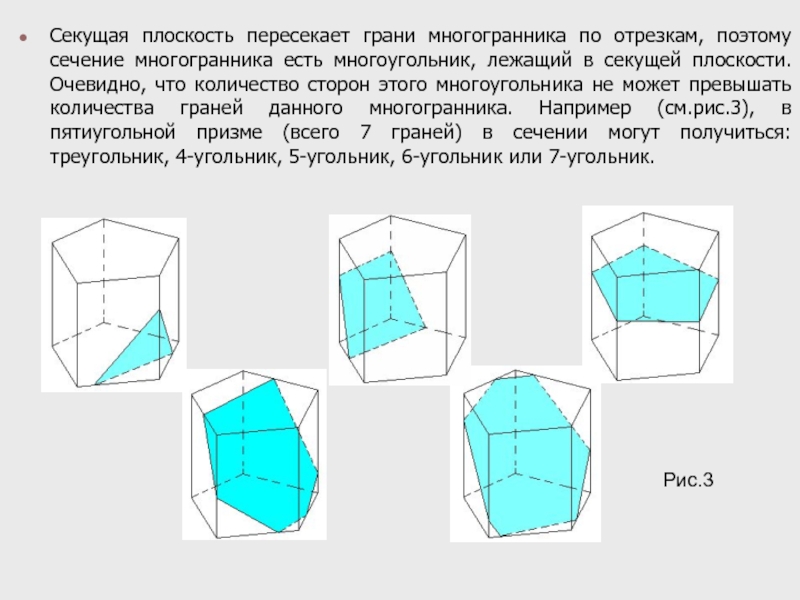
Слайд 3Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть
многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон этого многоугольника не может превышать количества граней данного многогранника. Например (см.рис.3), в пятиугольной призме (всего 7 граней) в сечении могут получиться: треугольник, 4-угольник, 5-угольник, 6-угольник или 7-угольник.
Рис.3
Слайд 4 Две плоскости пересекаются по прямой (эта аксиома и дала названию
метода – под «следом» понимается прямая пересечения какой-либо грани многогранника и секущей плоскости).
Получение «следа» сводится к получению двух точек, принадлежащих одновременно какой-нибудь грани многогранника и секущей плоскости (подумайте, почему именно двух!?).
Точки получаются как пересечение двух прямых, принадлежащих одной и той же плоскости.
ПРИМЕЧАНИЕ. Не забудьте, что прямая и плоскость являются бесконечными в пространстве фигурами!
Проследим на примере построение сечения куба плоскостью, заданной тремя данными точками M, N и K.
Получение «следа» сводится к получению двух точек, принадлежащих одновременно какой-нибудь грани многогранника и секущей плоскости (подумайте, почему именно двух!?).
Точки получаются как пересечение двух прямых, принадлежащих одной и той же плоскости.
ПРИМЕЧАНИЕ. Не забудьте, что прямая и плоскость являются бесконечными в пространстве фигурами!
Проследим на примере построение сечения куба плоскостью, заданной тремя данными точками M, N и K.
Слайд 5
A
B
C
D
B1
C1
D1
M
N
K
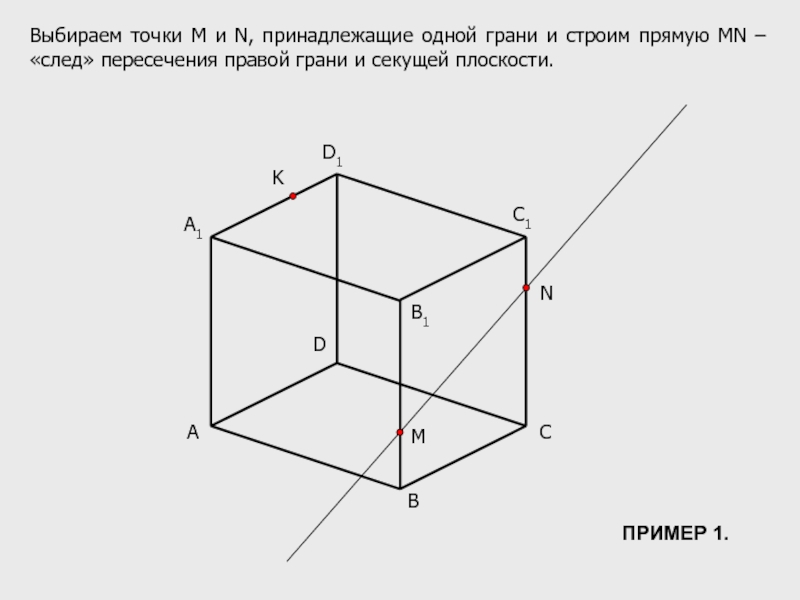
Выбираем точки М и N, принадлежащие одной грани и строим прямую
MN – «след» пересечения правой грани и секущей плоскости.
A1
ПРИМЕР 1.
Слайд 6
A
B
C
D
B1
C1
D1
M
N
K
A1
E
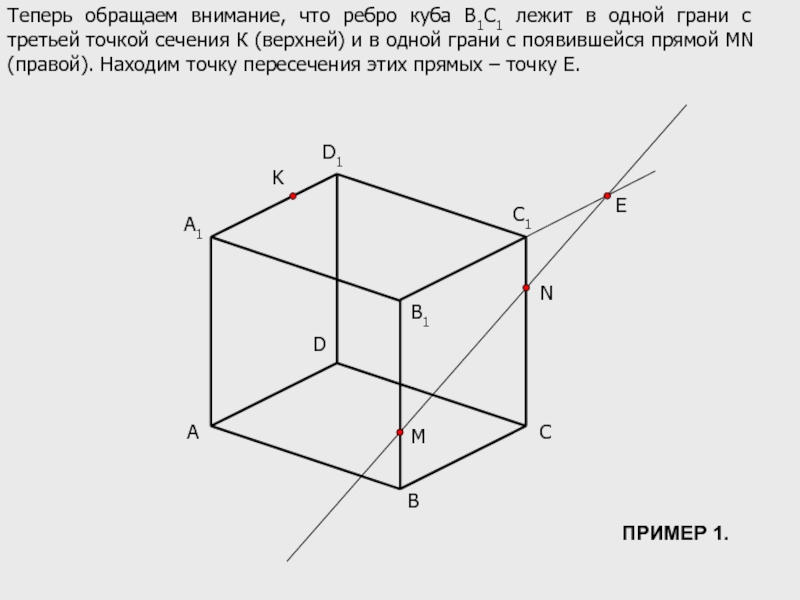
Теперь обращаем внимание, что ребро куба В1С1 лежит в одной грани
с третьей точкой сечения К (верхней) и в одной грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е.
ПРИМЕР 1.
Слайд 7
A
B
C
D
B1
C1
D1
M
N
K
A1
E
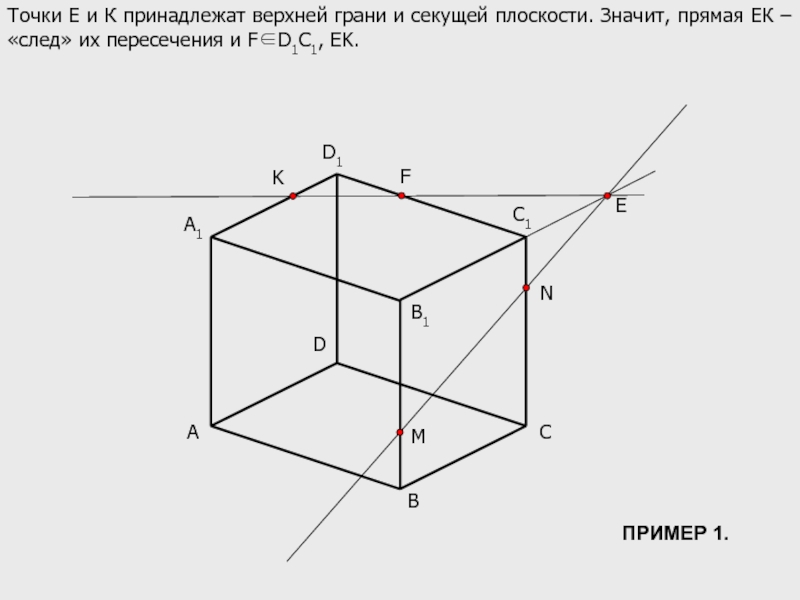
Точки Е и К принадлежат верхней грани и секущей плоскости. Значит,
прямая ЕК – «след» их пересечения и F∈D1C1, EK.
F
ПРИМЕР 1.
Слайд 8
A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
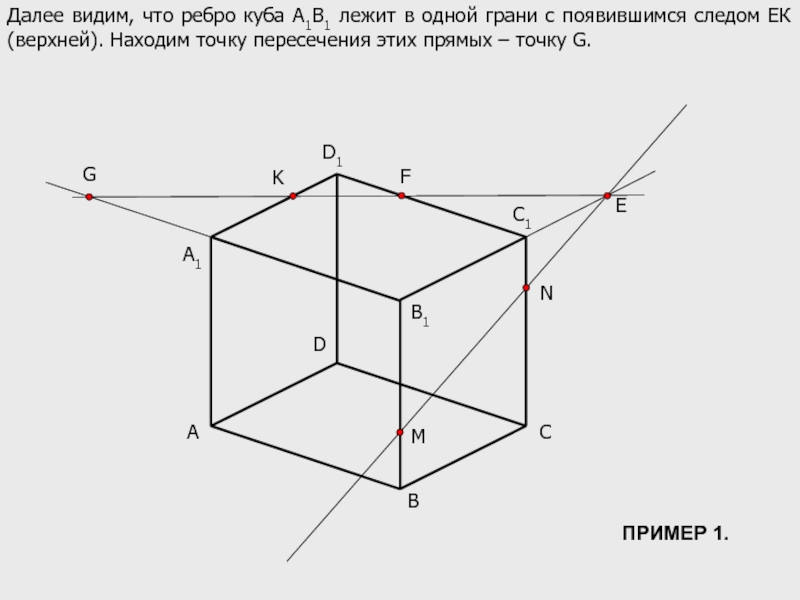
Далее видим, что ребро куба А1В1 лежит в одной грани с
появившимся следом ЕК (верхней). Находим точку пересечения этих прямых – точку G.
G
ПРИМЕР 1.
Слайд 9
A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
G
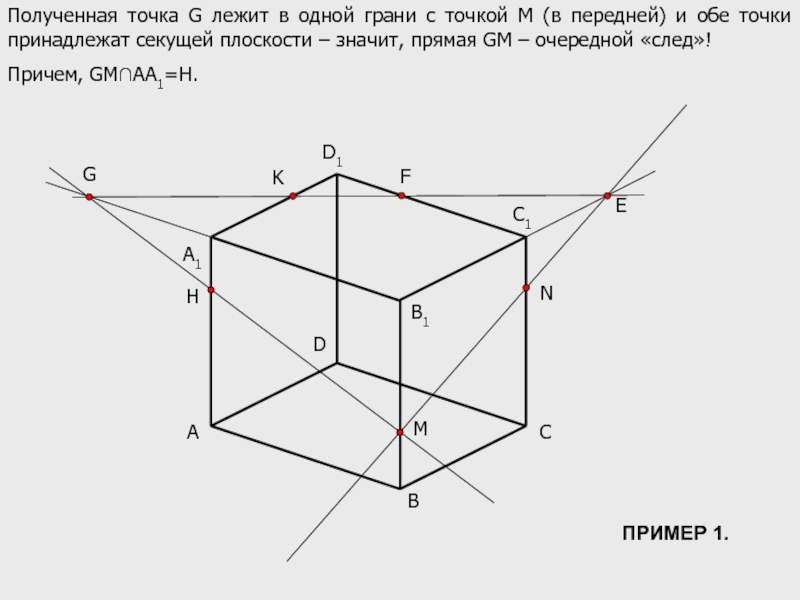
Полученная точка G лежит в одной грани с точкой М (в
передней) и обе точки принадлежат секущей плоскости – значит, прямая GM – очередной «след»!
Причем, GM∩АА1=Н.
Причем, GM∩АА1=Н.
H
ПРИМЕР 1.
Слайд 10
A
B
C
D
C1
D1
M
N
K
A1
E
F
G
H
Остается соединить отрезками все пары точек, лежащие в секущей плоскости и
в одной грани куба.
Полученный пятиугольник MNFKH – искомое сечение куба.
B1
ПРИМЕР 1.
Слайд 11
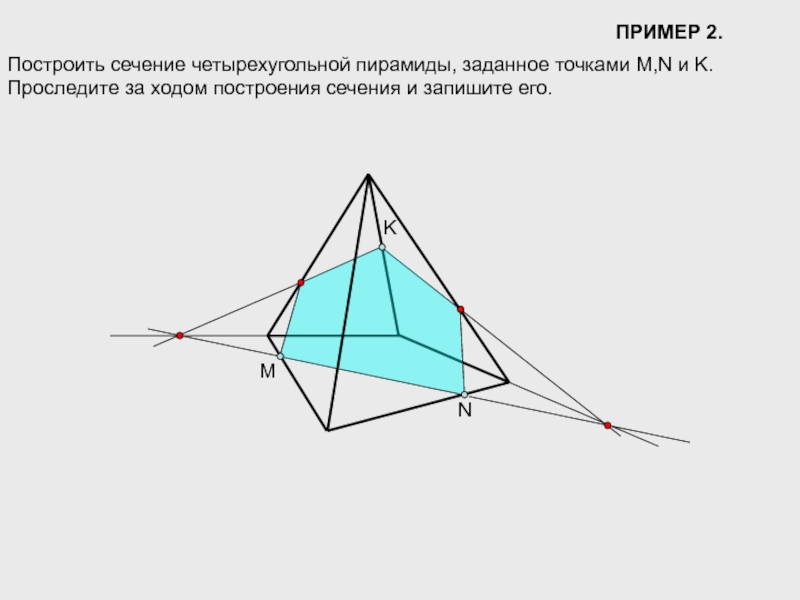
ПРИМЕР 2.
M
N
K
Построить сечение четырехугольной пирамиды, заданное точками M,N и K. Проследите
за ходом построения сечения и запишите его.
Слайд 12
ПРИМЕР 3.
Построить сечение пятиугольной призмы, заданное точками M,N и K. Проследите
за ходом построения сечения и запишите его.
M
N
K
Слайд 16Плоскость сечения может задаваться:
1) тремя точками, не лежащими на одной
прямой;
2) прямой и точкой, не лежащей на ней;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми.
Все эти случаи можно свести к первому, выбирая на прямых удобные для нас точки.
2) прямой и точкой, не лежащей на ней;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми.
Все эти случаи можно свести к первому, выбирая на прямых удобные для нас точки.
Слайд 17Заключение
Данный метод построения сечений многогранников можно применять, если найдется хотя бы
одна пара точек, лежащих в секущей плоскости и одной грани многогранника. После чего задача циклично алгоритмизируется в получение очередной точки и очередного «следа».
ПРИМЕЧАНИЕ. Если такой пары точек не найдется, то сечение строится методом параллельных проекций. Но это уже тема нового урока!
ПРИМЕЧАНИЕ. Если такой пары точек не найдется, то сечение строится методом параллельных проекций. Но это уже тема нового урока!
