Рожик Е.А.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение расписания минимальной длины для одностадийной системы с приборами различной производительности презентация
Содержание
- 1. Построение расписания минимальной длины для одностадийной системы с приборами различной производительности
- 2. Цель: разработка алгоритма построения расписания минимальной длины
- 3. -показать, что с помощью метода декомпозиции
- 4. Системы с идентичными приборами
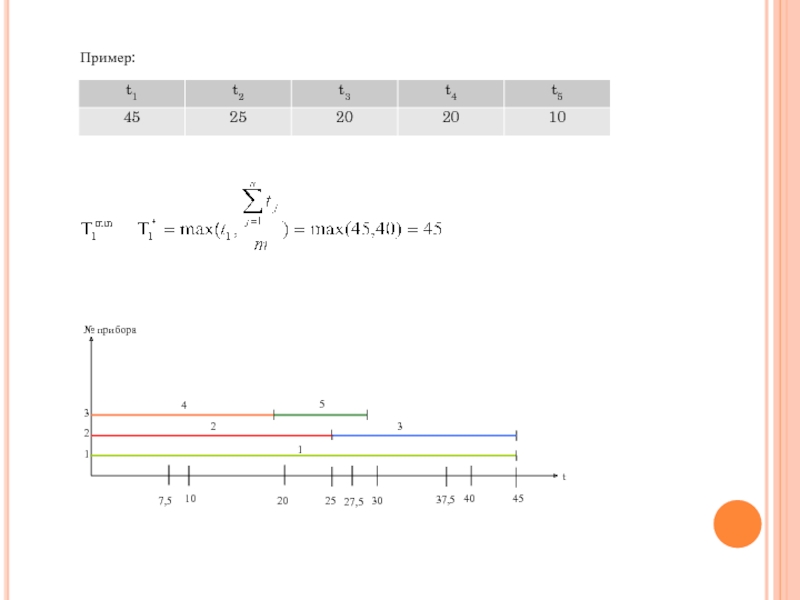
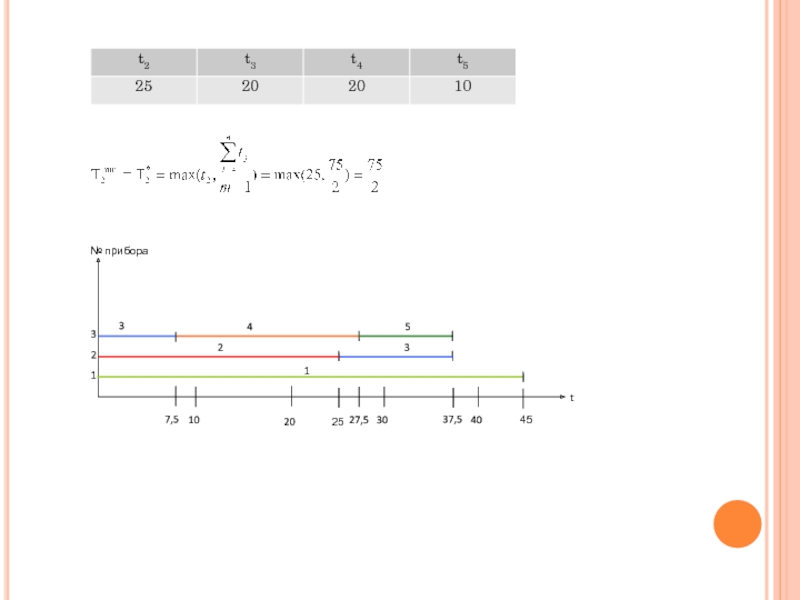
- 5. Пример:
- 10. Дубльтранспортная задача общего вида
- 11. и и , то , то
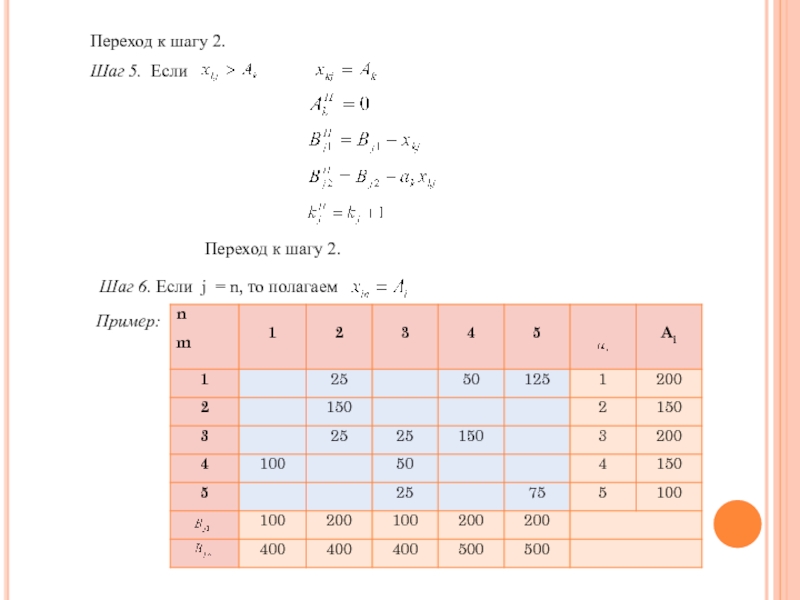
- 12. Переход к шагу 2. Шаг 5.
- 13. i = 1,..,m
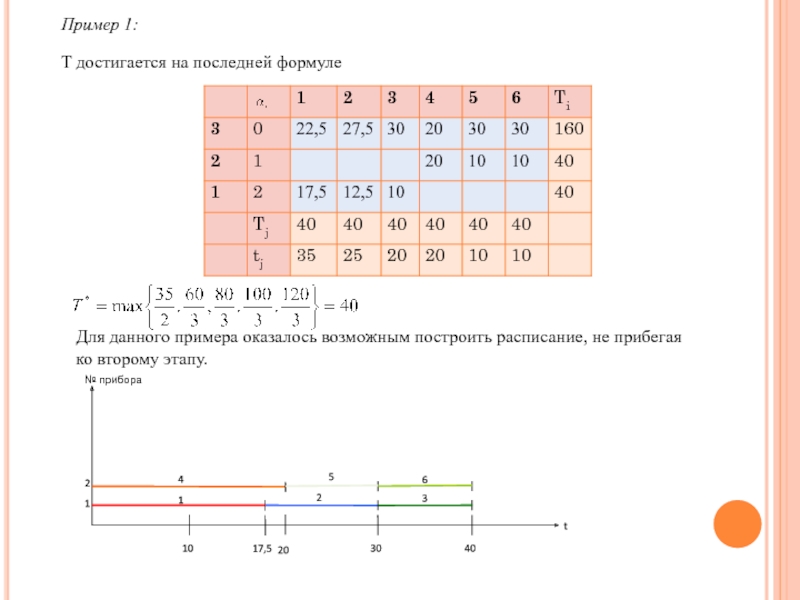
- 14. Пример 1: Т достигается на последней формуле
- 15. Пример 2: Т достигается не на последней формуле
- 18. Пример 3. 1) t=0, T = 19
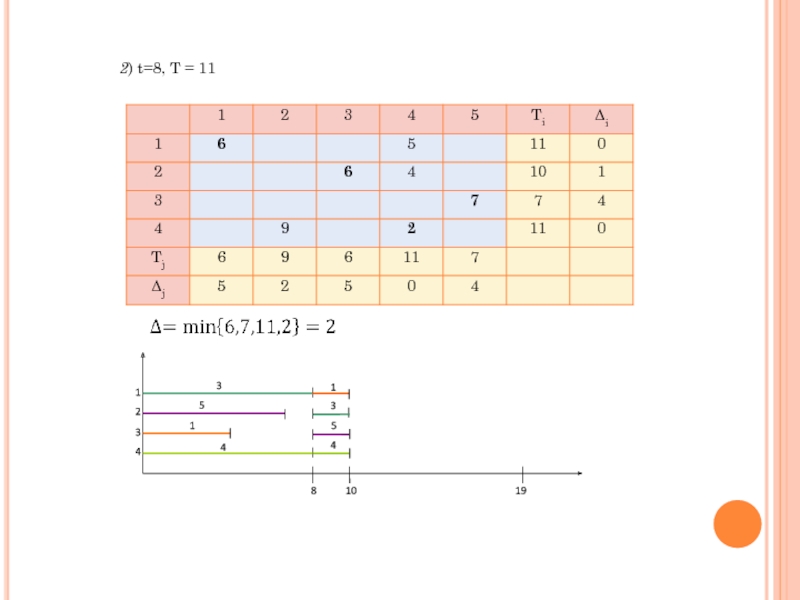
- 19. 2) t=8, T = 11
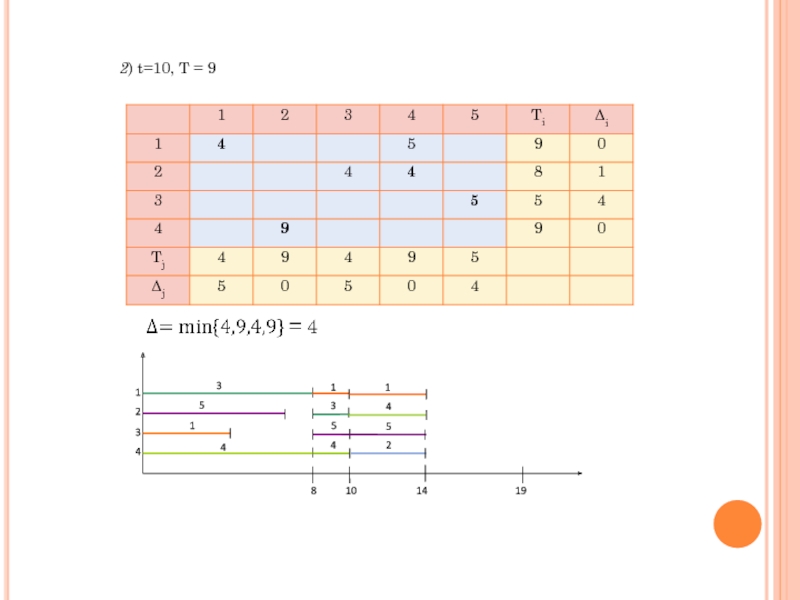
- 20. 2) t=10, T = 9
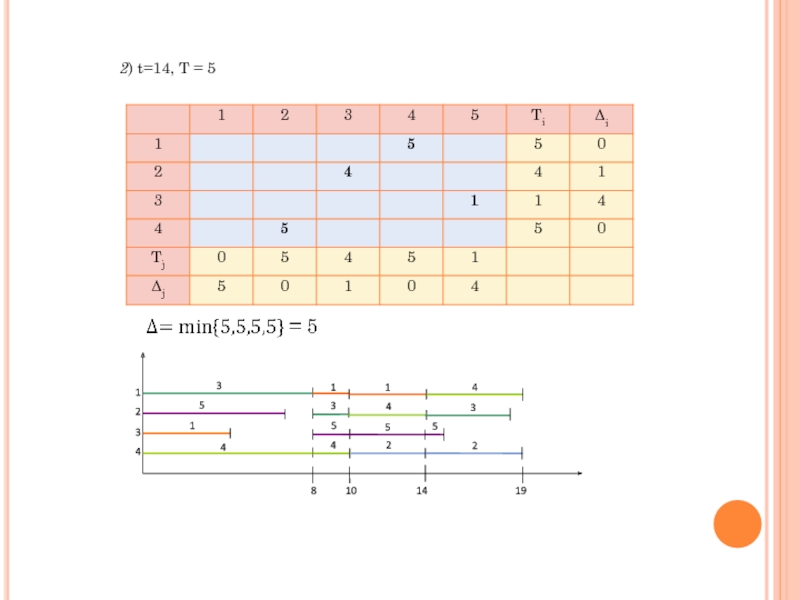
- 21. 2) t=14, T = 5
- 22. Заметим, если достигает своего максимума не на
- 23. Построение расписания для задачи с различными моментами поступления требований
- 24. Пример 4. 1 этап.
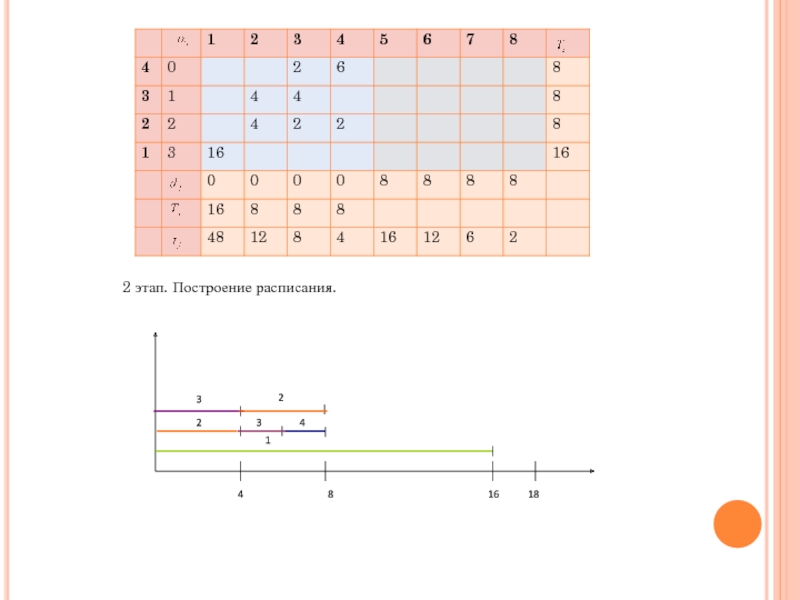
- 25. 2 этап. Построение расписания.
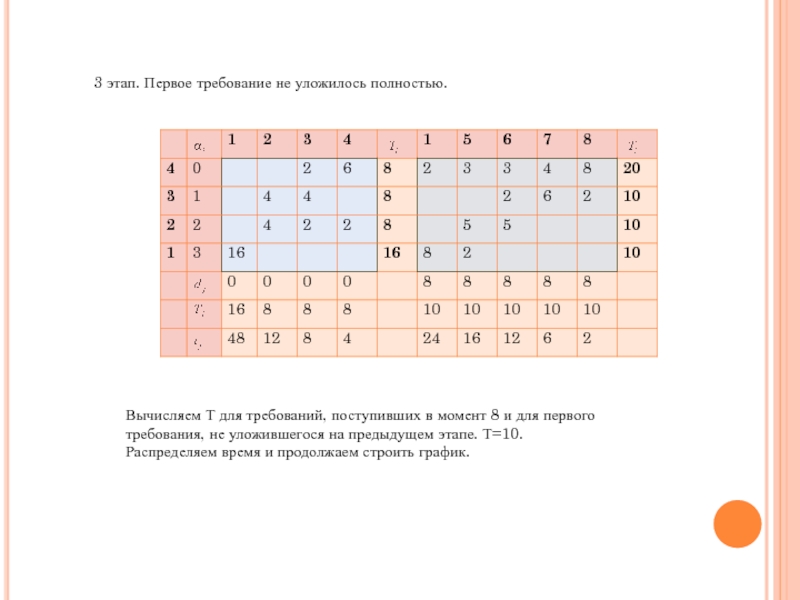
- 26. 3 этап. Первое требование не уложилось полностью.
- 28. Программная реализация
Слайд 1Построение расписания минимальной длины для одностадийной системы с приборами различной производительности
Исполнитель
Руководитель
Аснина
Слайд 2Цель: разработка алгоритма построения расписания минимальной длины для системы с приборами
Цели и задачи выпускной работы
Слайд 3 -показать, что с помощью метода декомпозиции получается распределение времени с минимально
Цели и задачи выпускной работы
Слайд 4Системы с идентичными приборами
– время, в течение которого j - е
Слайд 7
j = 1,..,n (2)
j = 1,..,n
i = 1,…,m, j = 1,..,n
– время, в течение которого j - е требование будет обслуживаться i-м прибором;
- длительность обслуживания j-го требования на i-м приборе.
Слайд 10Дубльтранспортная задача общего вида
i = 1,..,m
j = 1,..,n
j = 1,..,n
Необходимое условие совместности:
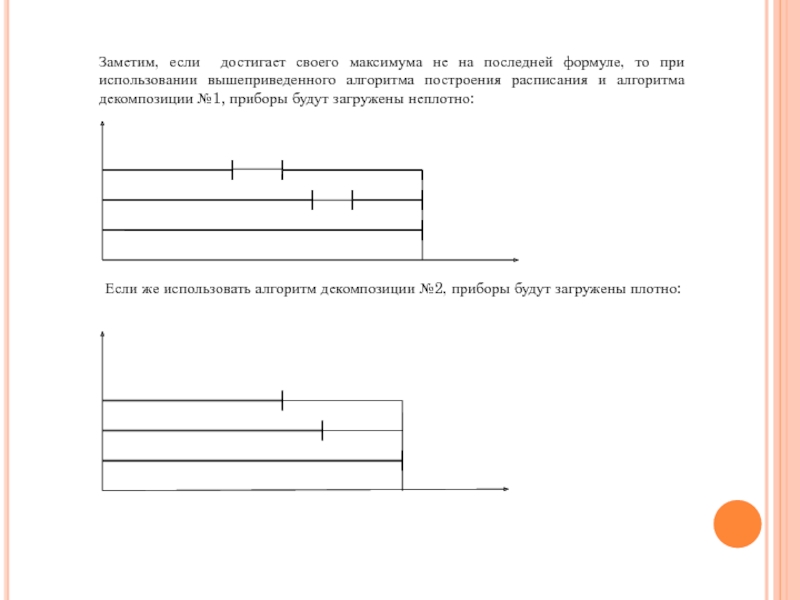
Слайд 22Заметим, если достигает своего максимума не на последней формуле, то при
Если же использовать алгоритм декомпозиции №2, приборы будут загружены плотно:
Слайд 24Пример 4.
1 этап. T=16, достигается на первой формуле.
Пересчитываем T
Т=8, достигается на последней формуле.
Слайд 263 этап. Первое требование не уложилось полностью.
Вычисляем Т для требований, поступивших
требования, не уложившегося на предыдущем этапе. Т=10.
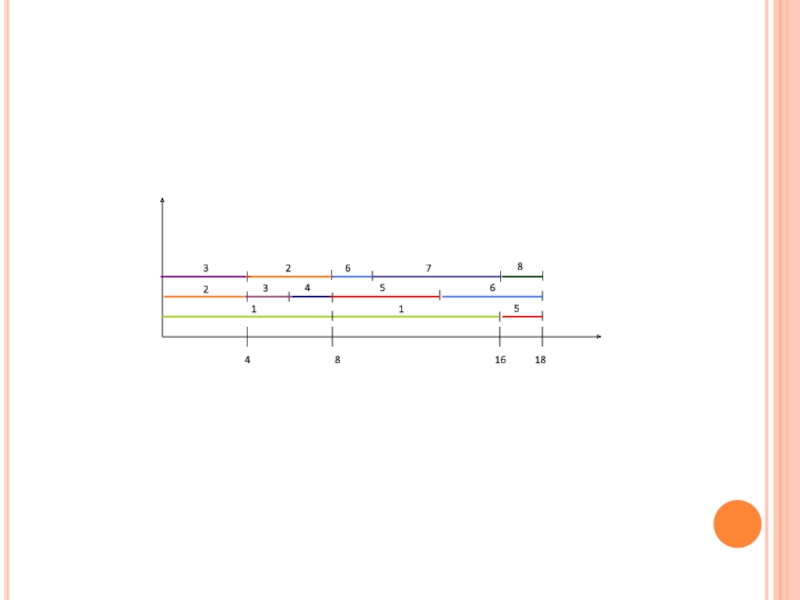
Распределяем время и продолжаем строить график.
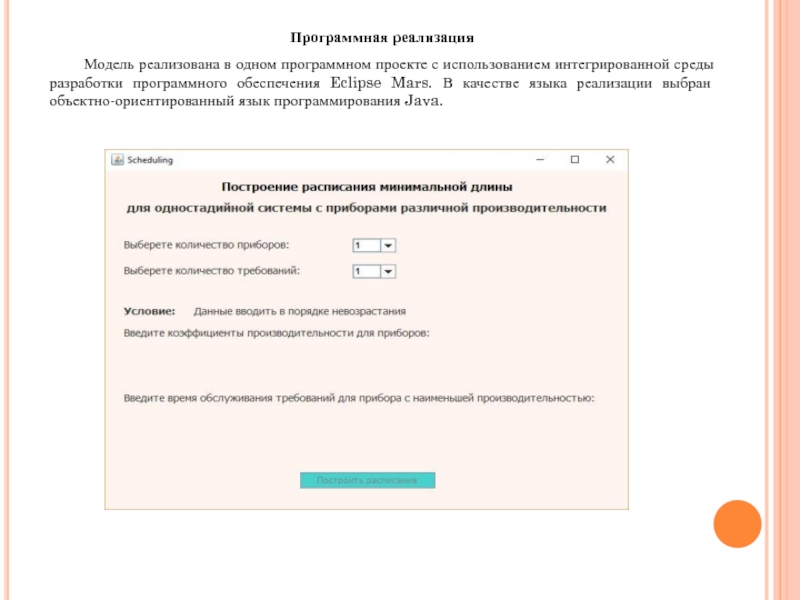
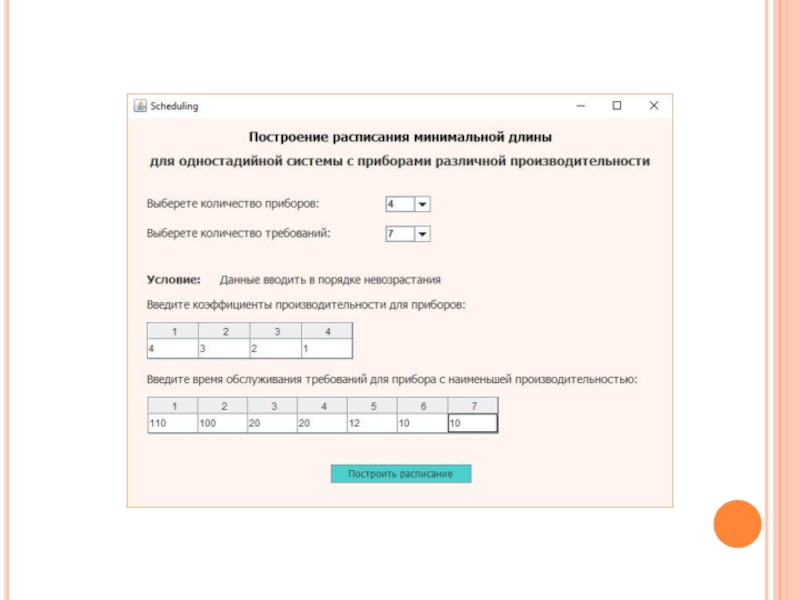
Слайд 28Программная реализация
Модель реализована в одном программном проекте