- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение графиков функций с помощью сдвигов и деформаций презентация
Содержание
- 1. Построение графиков функций с помощью сдвигов и деформаций
- 2. Содержание: Вступление. График функции
- 3. Дорогие ребята! Изучая курс
- 5. Построить график функции у=f(x)+b, зная график
- 6. Построить график функции у=mf(x), зная график функции
- 7. Построить график функции у=f(kx), зная график функции
- 8. Построить график функции у= - mf(kx+a)+b.
- 9. Применение метода сдвигов и
- 10. Искомая функция Рис.8
- 11. Модули.
- 12. если если Пример: Искомая функция Рис.9 Рис.10 Рис.11 Рис.12
- 13. На основании модуля имеем:
- 14. Построить график функции y=|f
- 15. Упражнения. Задание: 1)
- 16. Задача – исследование.
Слайд 2Содержание:
Вступление.
График функции
График функции .
График функции .
График функции .
Композиция сдвигов и деформаций (график сложной функции).
Применение метода сдвигов и деформаций при построении графиков тригонометрических функций.
Построение графиков функций, содержащих знак модуля: а) график функции у = f(|x|); б) график функции у = |f(x)|; в) график функции у = |f(|x|)|;
Упражнения.
Задача – исследование.
Тест.
Основные результаты.
Слайд 3Дорогие ребята!
Изучая курс алгебры в основной школе, Вы
, строить графики следующих функций:
Венцом всех этих преобразований является график функции:
Кроме этого, Вы научитесь строить графики функций, содержащих знак модуля, которые обычно вызывают затруднения. Это функции трех видов:
В дальнейшем Вы рассмотрите поэтапное построение графиков всех этих функций и примените полученные знания при выполнении упражнений.
Слайд 4
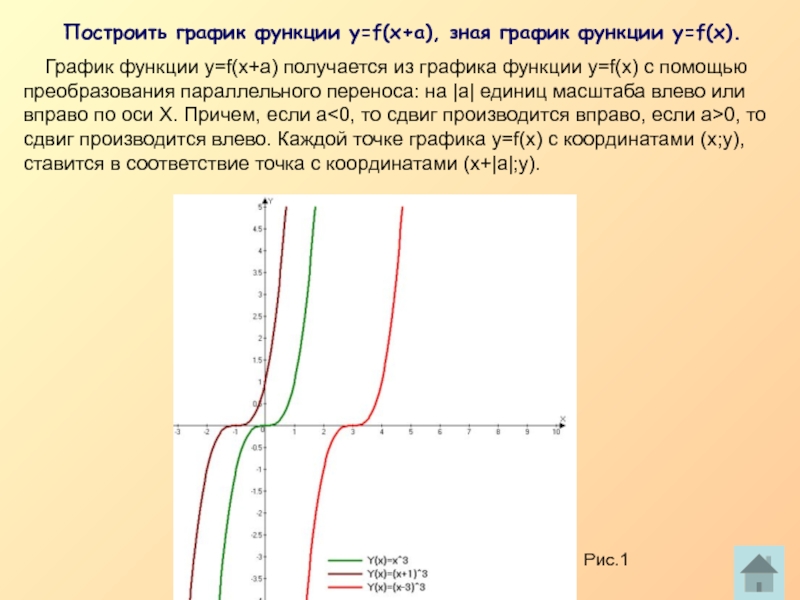
Построить график функции у=f(x+a), зная
График функции у=f(x+a) получается из графика функции у=f(x) с помощью преобразования параллельного переноса: на |а| единиц масштаба влево или вправо по оси Х. Причем, если а<0, то сдвиг производится вправо, если а>0, то сдвиг производится влево. Каждой точке графика у=f(x) с координатами (х;у), ставится в соответствие точка с координатами (х+|а|;у).
Рис.1
Слайд 5
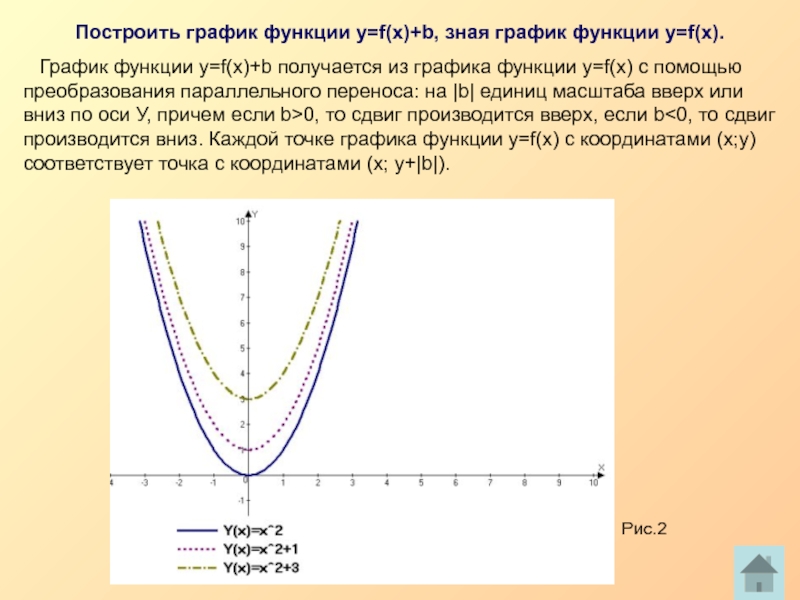
Построить график функции у=f(x)+b, зная график функции у=f(x).
График функции
Рис.2
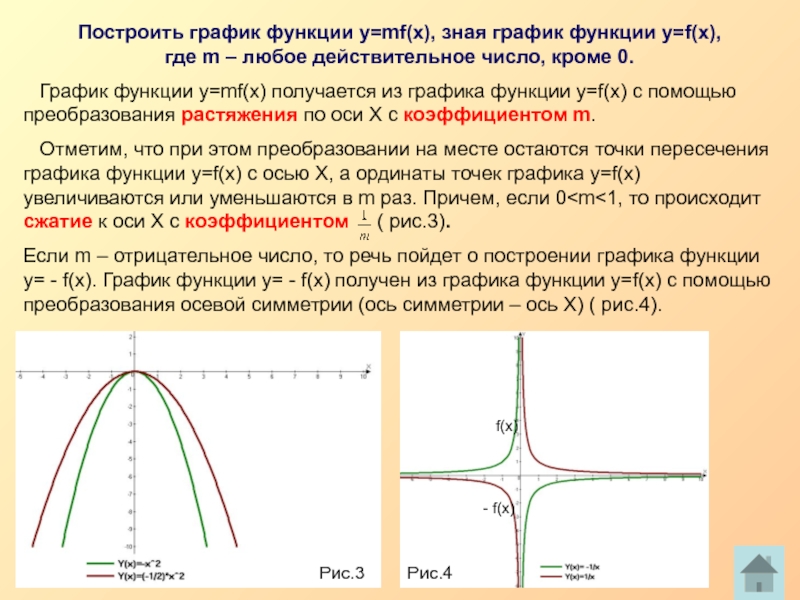
Слайд 6Построить график функции у=mf(x), зная график функции у=f(x),
График функции у=mf(x) получается из графика функции у=f(x) с помощью преобразования растяжения по оси Х с коэффициентом m.
Отметим, что при этом преобразовании на месте остаются точки пересечения графика функции у=f(x) с осью Х, а ординаты точек графика у=f(x) увеличиваются или уменьшаются в m раз. Причем, если 0
Рис.4
Рис.3
f(x)
- f(x)
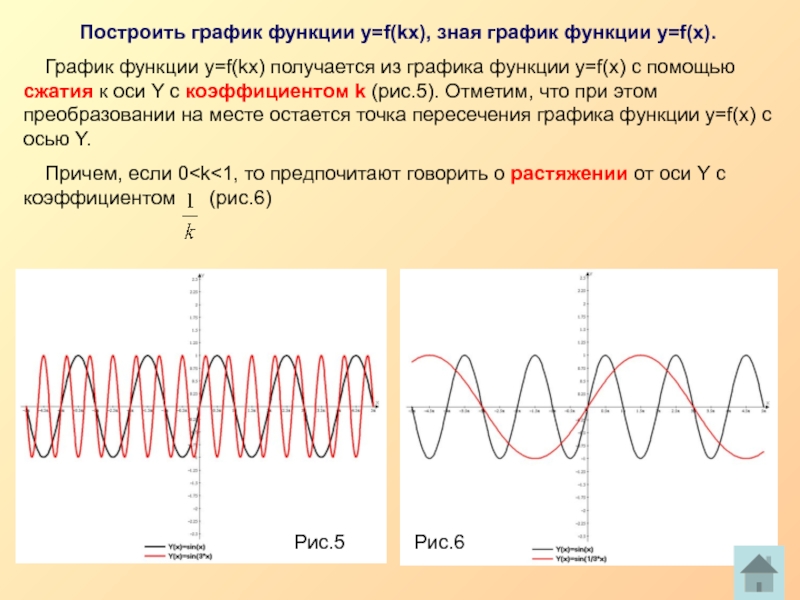
Слайд 7Построить график функции у=f(kx), зная график функции у=f(x).
График функции
Причем, если 0
Рис.6
Рис.5
Слайд 8
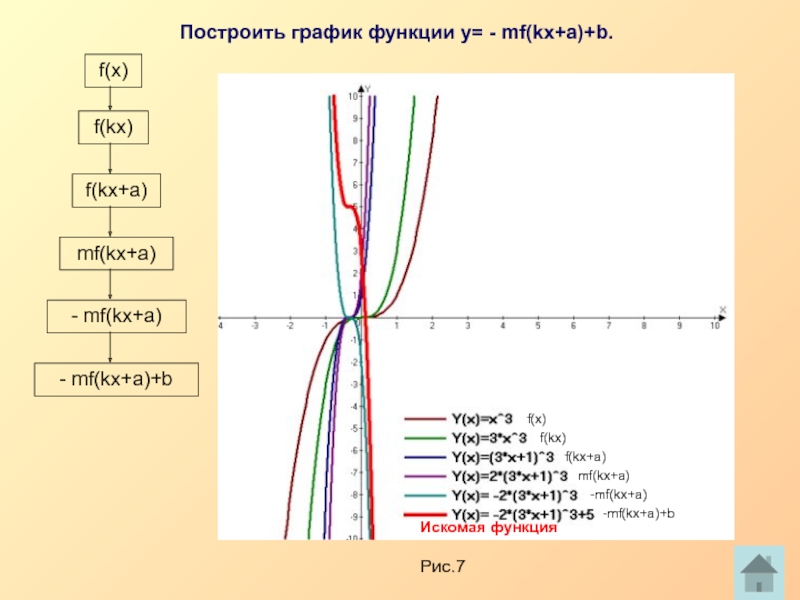
Построить график функции у= - mf(kx+a)+b.
f(x)
f(kx)
f(kx+a)
mf(kx+a)
- mf(kx+a)
- mf(kx+a)+b
Рис.7
f(x)
f(kx)
f(kx+a)
mf(kx+a)
-mf(kx+a)
-mf(kx+a)+b
Искомая функция
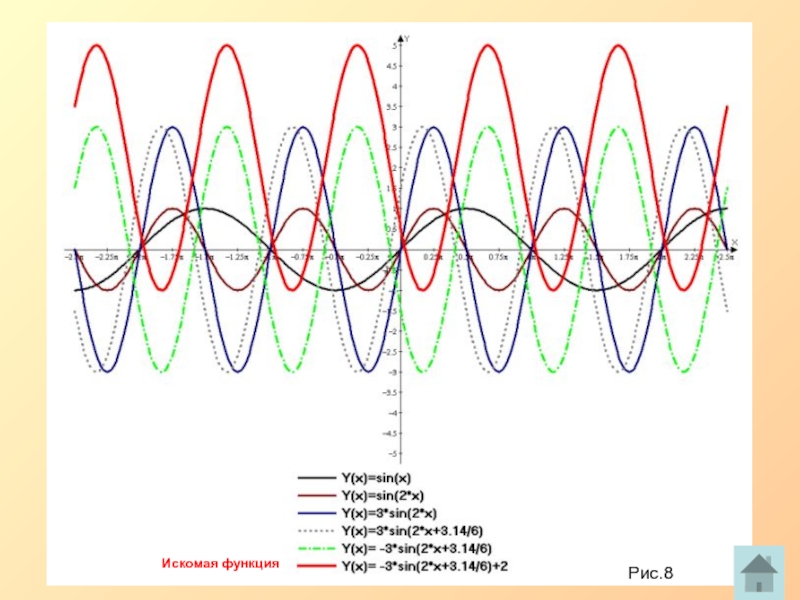
Слайд 9
Применение метода сдвигов и деформаций при построении графиков тригонометрических функций.
- уравнение гармонических колебаний.
имеют определен-
ный физический смысл:
амплитуда колебаний ( – А, если А<0);
частота колебаний;
начальная фаза колебаний.
Рассмотрим уравнение вида:
Чтобы построить график этой функции, нужно над полуволной синусоиды осуществить следующие преобразования:
Сжать ее к оси Y с k=2.
Растянуть от оси X с k=3.
Сжатую и растянутую полуволну сдвинуть вдоль оси Х на влево.
Построить полуволну синусоиды, симметрично полученной относительно оси Х.
Сдвинуть полученную полуволну синусоиды вверх на 2 единицы масштаба.
С помощью полученной полуволны получить искомый график.
Слайд 11
Модули.
Для построения всех типов графиков достаточно хорошо понимать
если х
если х < 0.
Следовательно, график функции y=f(|x|) состоит из двух графиков: y=f(x) – в правой полуплоскости, y=f(-x) – в левой полуплоскости.
Правило 1. Если функция y=f(|x|) – четная, то для построения ее графика достаточно построить график функции y=f(x) для всех х из области определения и отразить полученную часть симметрично оси ординат.
Знание этого правила облегчает построение графиков функций вида y=f(|x|).
Слайд 13
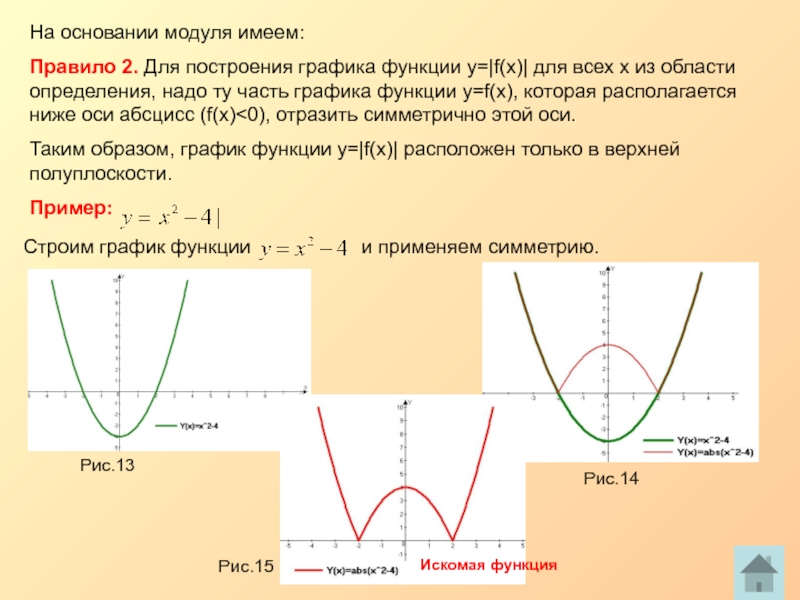
На основании модуля имеем:
Правило 2. Для построения графика функции y=|f(x)| для
Таким образом, график функции y=|f(x)| расположен только в верхней полуплоскости.
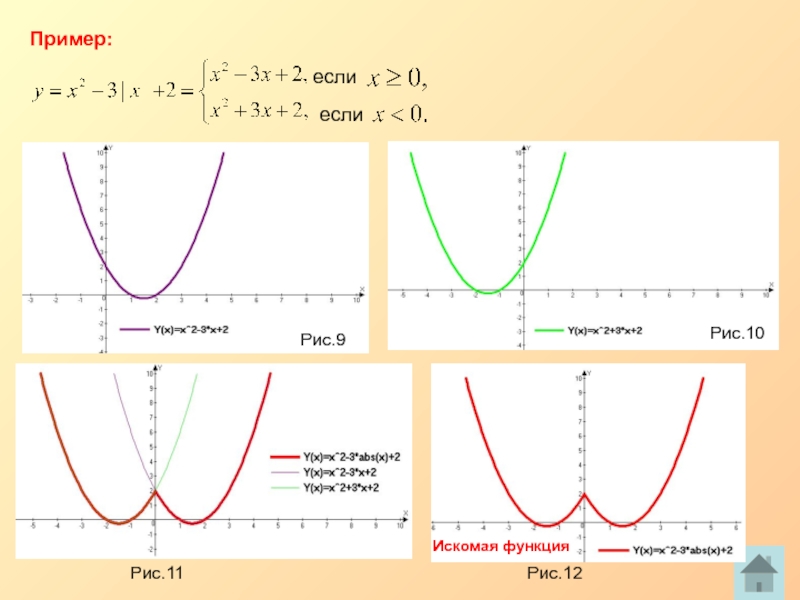
Пример:
Строим график функции и применяем симметрию.
Искомая функция
Рис.13
Рис.14
Рис.15
Слайд 14
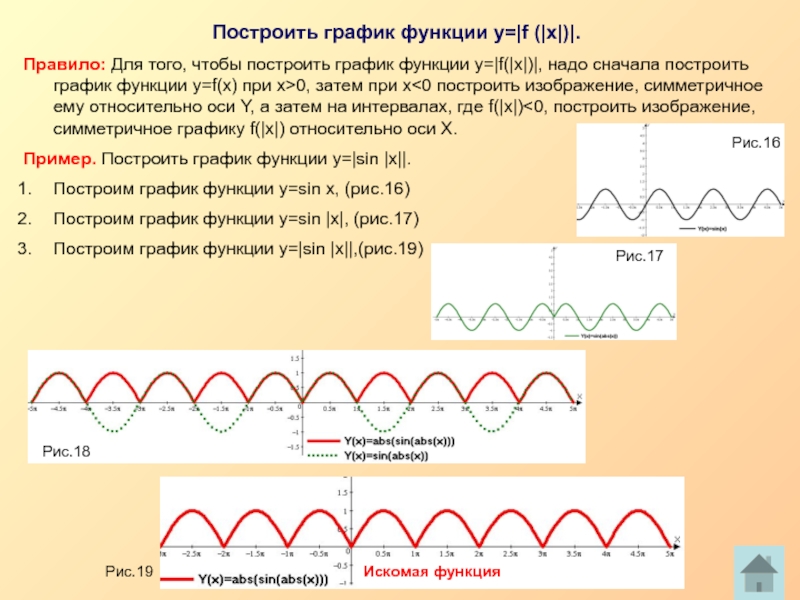
Построить график функции y=|f (|x|)|.
Правило: Для того, чтобы построить график функции
Пример. Построить график функции y=|sin |x||.
Построим график функции y=sin x, (рис.16)
Построим график функции y=sin |x|, (рис.17)
Построим график функции y=|sin |x||,(рис.19)
Рис.16
Рис.17
Рис.18
Рис.19
Искомая функция
Слайд 15
Упражнения.
Задание: 1) Разбить функцию на подфункции. 2) Построить графики подфункций разным
«Запомните, друзья, Суть истины такой Теория мертва без практики живой»
«Сложность задач повышаем Решенье найти предлагаем»
«В задачах тех ищи удачу Где получить рискуешь сдачу»
Слайд 16
Задача – исследование.
Вспомним все, что мы учили! Ничего, ведь, не забыли?
Дана функция .
В программе AGRAPHER:
Осуществите осевую симметрию графика относительно оси Х.
Выполните сдвиг графика на 2 единицы вверх.
Выполните сдвиг графика на 1 единицу влево.
Произведите сжатие графика в 2 раза к оси Y.
Отразите ту часть графика, которая располагается ниже оси абсцисс, симметрично этой оси.
Результат построения сохраните в своей папке под именем «Исследование».
Слайд 17
Основные результаты.
Ребята, Вы систематизировали и обобщили правила сдвигов и деформаций,
Вы научились строить графики функций: