- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поняття стійкості автоматичної системи. Математичні ознаки стійкості. Критерій Гурвіца презентация
Содержание
- 1. Поняття стійкості автоматичної системи. Математичні ознаки стійкості. Критерій Гурвіца
- 2. План лекції Поняття стійкість Математичні умови стійкості Критерій стійкості Гурвіца.
- 3. 1. Поняття стійкість Незбуреним рухом САУ називають
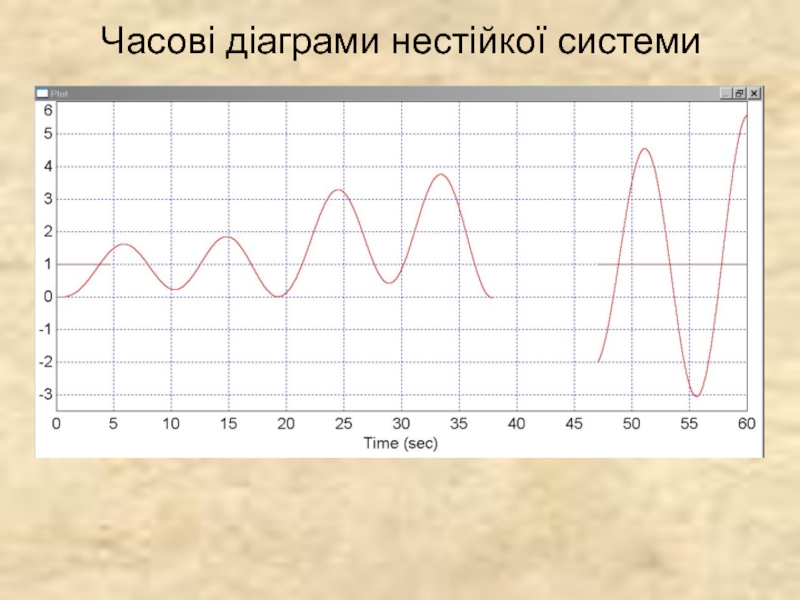
- 4. Часові діаграми нестійкої системи
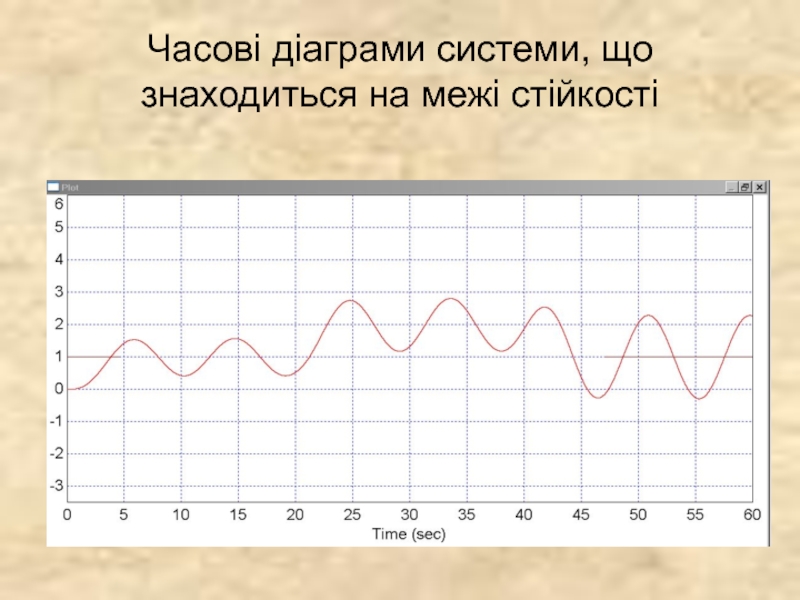
- 5. Часові діаграми системи, що знаходиться на межі стійкості
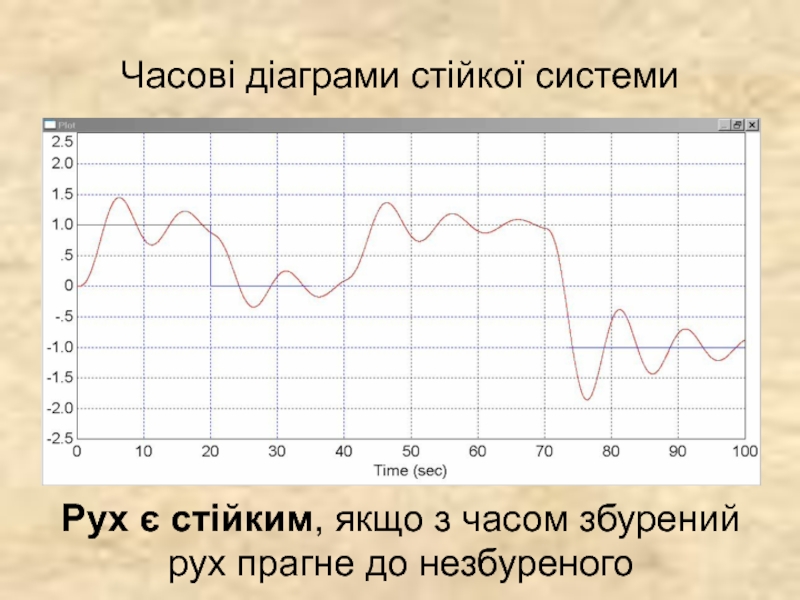
- 6. Часові діаграми стійкої системи Рух є стійким,
- 7. Ляпунов, Александр Михайлович (25 мая (6 июня)
- 8. 2. Математичні умови стійкості Рішення рівняння, що
- 9. Рішення однорідного рівняння може бути отримано у
- 10. Необхідна і достатня ознака стійкості лінійного об'єкту
- 11. 3. Алгебраїчний критерій Гурвіца Критерій стійкості –
- 12. Адольф Гурвиц (нем. Adolf Hurwitz), 26 березня
- 13. Якщо всі корені алгебраїчного рівняння:
- 14. Визначник Гурвіца:
- 15. Визначники Гурвіца для системи 4-го порядку: Визначники Гурвіца для системи 3-го порядку:
- 16. Завдання на самопідготовку: Абрамов Ю.А. “Основы пожарной автоматики“ стор. 122-130
План лекції Поняття стійкість Математичні умови стійкості Критерій стійкості Гурвіца.
Слайд 1Поняття стійкості автоматичної системи. Математичні ознаки стійкості. Критерій Гурвіца.
Лекція №5.
Слайд 31. Поняття стійкість
Незбуреним рухом САУ називають рух ідеальної (безінерційної) системи під
впливом заданого зовнішнього сигналу.
Збуреним називають рух реальної САУ під впливом заданого зовнішнього сигналу.
Збуреним називають рух реальної САУ під впливом заданого зовнішнього сигналу.
Стійкість об'єкту полягає в його здатність зберігати свої властивості в умовах, що змінюються.
Слайд 6Часові діаграми стійкої системи
Рух є стійким, якщо з часом збурений рух
прагне до незбуреного
Слайд 7Ляпунов, Александр Михайлович (25 мая (6 июня) 1857, Ярославль — 3
ноября 1918, Одесса) — русский математик и механик, академик Петербургской Академии наук с 1901 года, член-корреспондент Парижской академии наук. Важнейшим достижением Ляпунова стало создание теории устойчивости равновесия и движения механических систем.
Слайд 82. Математичні умови стійкості
Рішення рівняння, що відповідає збуреному руху:
Для того,
щоб система була стійкою, необхідно щоб з часом хпер(t) зменшувалась
Слайд 9Рішення однорідного рівняння може бути отримано у вигляді:
λ i - корені
характеристичного рівняння :
Для дійсних коренів характеристичного рівняння необхідно щоб виконувалась умова:
Для пари комплексно-споряджених коренів :
необхідно щоб:
Слайд 10Необхідна і достатня ознака стійкості лінійного об'єкту полягає в тому, щоб
усі корені характеристичного рівняння мали негативну дійсну частину.
графічна інтерпритація
Слайд 113. Алгебраїчний критерій Гурвіца
Критерій стійкості – це умови, виконання яких необхідно
і достатньо, щоб усі корені характеристичного рівняння системи, розташовувались в лівій напівплощині коренів, то б то САУ була стійкою.
Слайд 12Адольф Гурвиц (нем. Adolf Hurwitz), 26 березня 1859, Хильдесхайм — 18
листопада 1919, Цюрих) — немецкий математик.
Слайд 13
Якщо всі корені алгебраїчного рівняння:
розташовані зліва, т.т. мають від’ємну дійсну
частину, якщо коефіцієнти
i всі визначники Гурвіца починаючи з головного визначника більше нуля, то система стійка.
