- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие цилиндра презентация
Содержание
- 1. Понятие цилиндра
- 2. План урока: 1. Понятие цилиндра
- 3. образующая цилиндрическая поверхность произвольная кривая
- 4. ЦИЛИНДРИЧЕСКОЕ ТЕЛО (Цилиндр) образующие О1
- 5. Цилиндр основанием которого служит
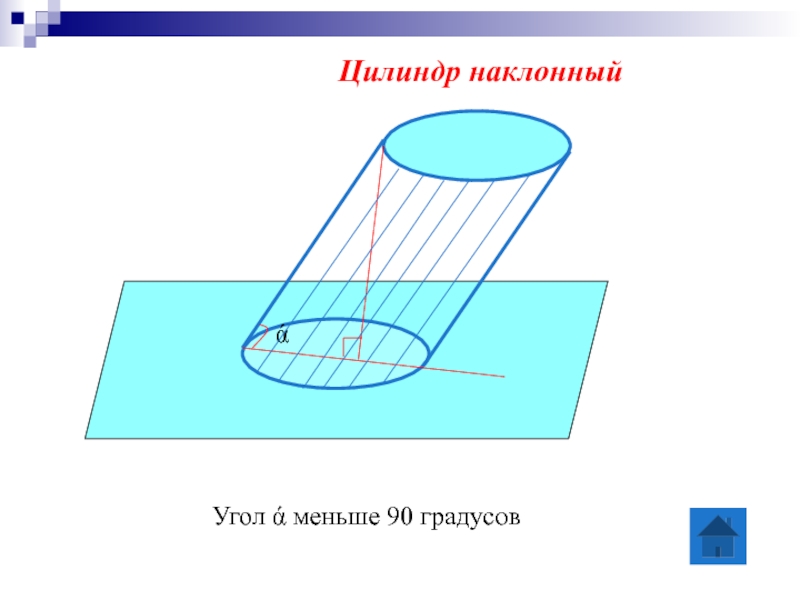
- 6. Угол ά меньше 90 градусов Цилиндр наклонный
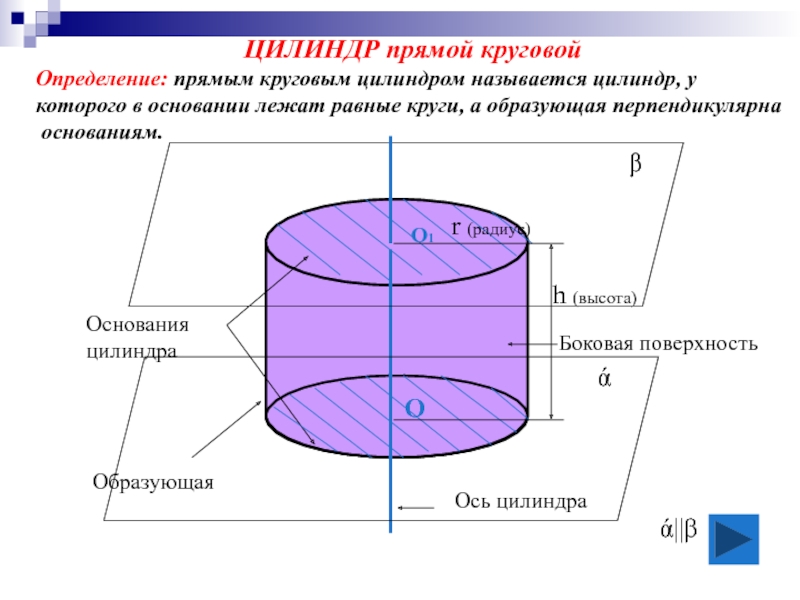
- 7. ЦИЛИНДР прямой круговой Определение: прямым круговым цилиндром
- 8. 3. Радиусом цилиндра называется радиус его основания.
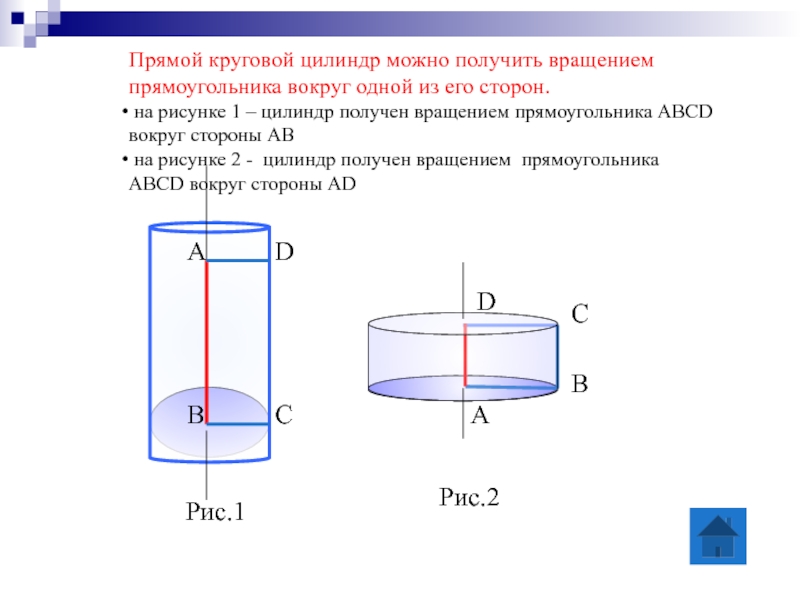
- 9. А D В С Рис.1
- 10. А В С D О О1
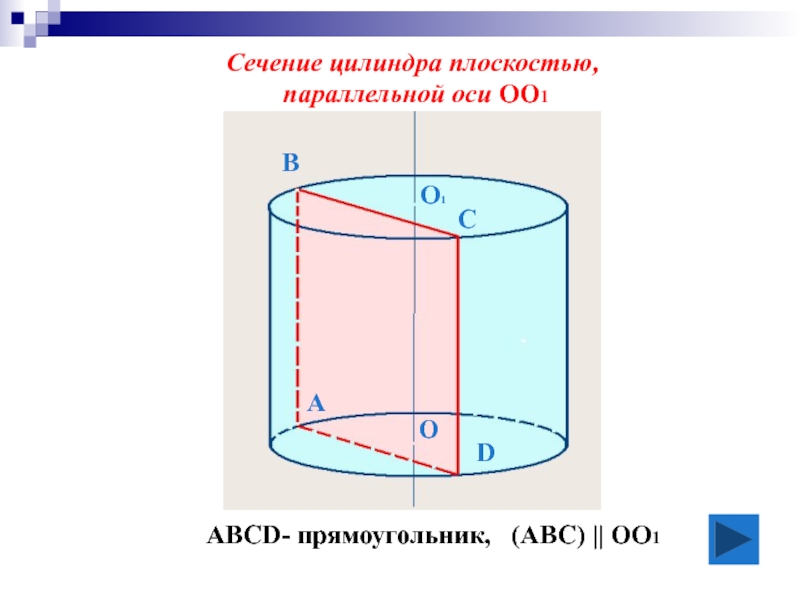
- 11. А В С D АВСD- прямоугольник,
- 12. α ┴ OO1 , сечение – круг,
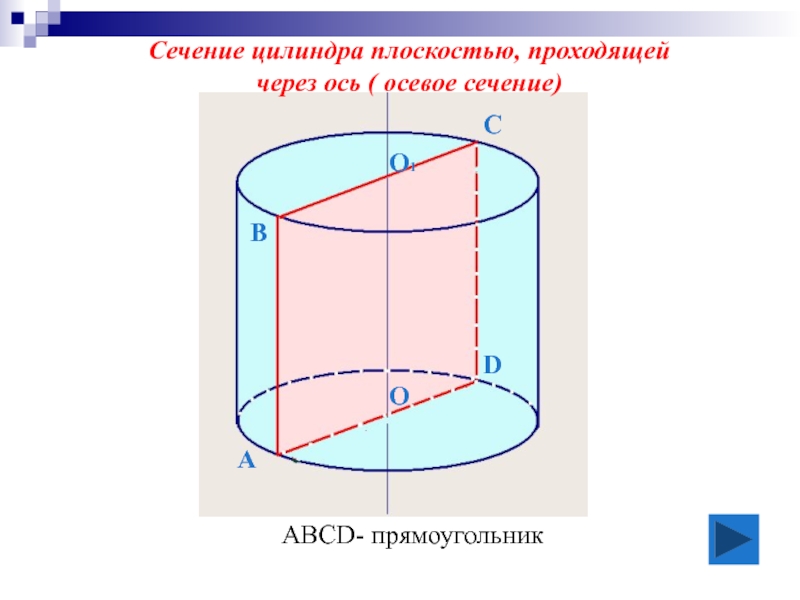
- 13. Сечение цилиндра плоскостью, проходящей
- 14. АВВ1А1- прямоугольник В А1 В1 А
- 15. «Боковые и полные поверхности подобных цилиндров
- 16. Внимание!
- 17. Задача Первый вариант Вычислите полную и боковую
- 18. Историческая справка Слово «цилиндр» происходит от
- 39. Ответь на вопросы 1. Назови элементы цилиндра
- 40. Домашнее задание: п. 53 - 54 №
Слайд 2План урока:
1. Понятие цилиндра
2. Прямой круговой цилиндр и его элементы
3. Сечение
4. Площадь боковой и полной
поверхности цилиндра
5. Цилиндры вокруг нас
6. Проверочная работа
7. Домашнее задание
Слайд 3
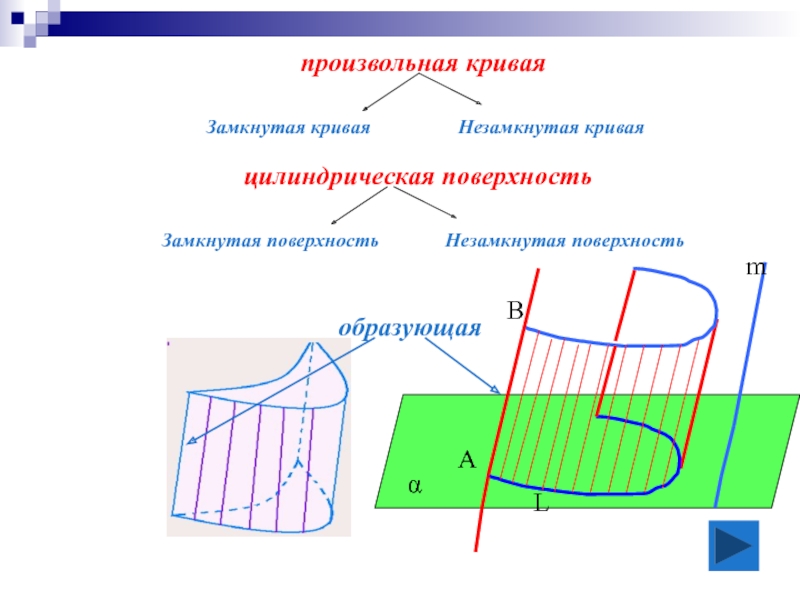
образующая
цилиндрическая поверхность
произвольная кривая
Незамкнутая поверхность
Замкнутая кривая
Незамкнутая кривая
Замкнутая поверхность
А
m
α
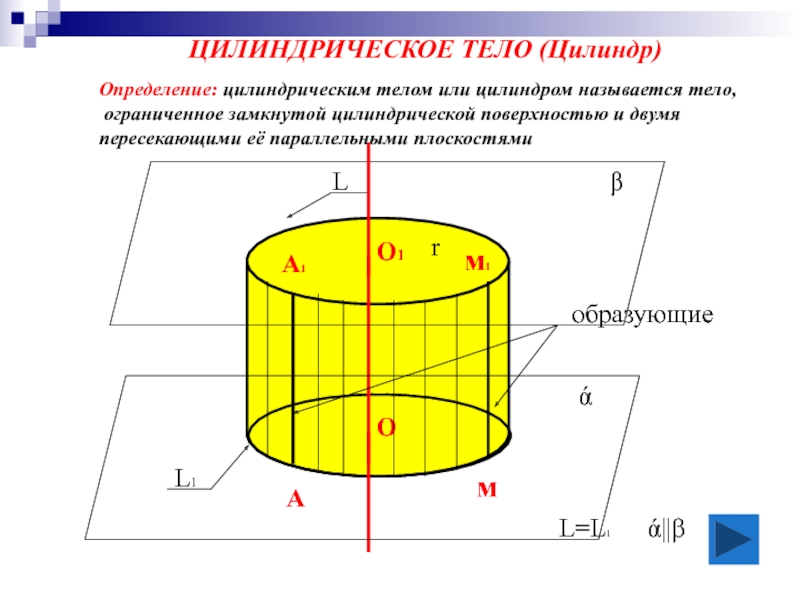
Слайд 4ЦИЛИНДРИЧЕСКОЕ ТЕЛО (Цилиндр)
образующие
О1
О
ά
β
м1
м
r
ά||β
L
L1
L=L1
А
А1
Определение: цилиндрическим телом или цилиндром называется тело,
ограниченное замкнутой
пересекающими её параллельными плоскостями
Слайд 5
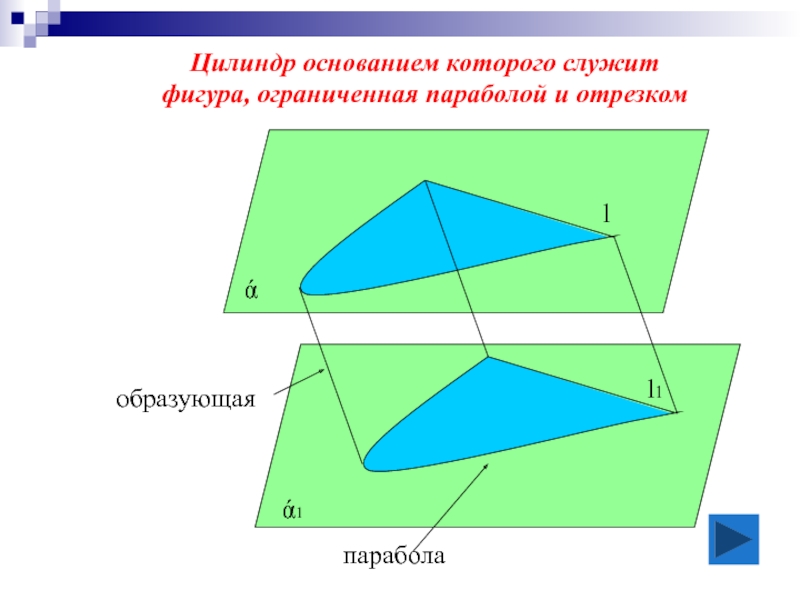
Цилиндр основанием которого служит
фигура, ограниченная параболой и отрезком
l
l1
образующая
ά
ά1
парабола
Слайд 7ЦИЛИНДР прямой круговой
Определение: прямым круговым цилиндром называется цилиндр, у
которого в
основаниям.
ά||β
Образующая
Слайд 83. Радиусом цилиндра называется радиус его основания.
4. Высота цилиндра- расстояние между
в прямом цилиндре она совпадает с образующей.
5. Ось цилиндра- прямая, проходящая через центры оснований,
она параллельна образующим.
1. Боковой поверхностью цилиндра называется часть
цилиндрической поверхности, заключенная между
параллельными плоскостями.
2. Основания - часть плоскостей, отсекаемых цилиндрической
поверхностью.
Слайд 9
А
D
В
С
Рис.1
Прямой круговой цилиндр можно получить вращением
прямоугольника вокруг одной из его
на рисунке 1 – цилиндр получен вращением прямоугольника АВСD
вокруг стороны АВ
на рисунке 2 - цилиндр получен вращением прямоугольника
АВСD вокруг стороны AD
Слайд 10
А
В
С
D
О
О1
Сечение цилиндра плоскостью, проходящей
через ось ( осевое сечение)
АВСD- прямоугольник
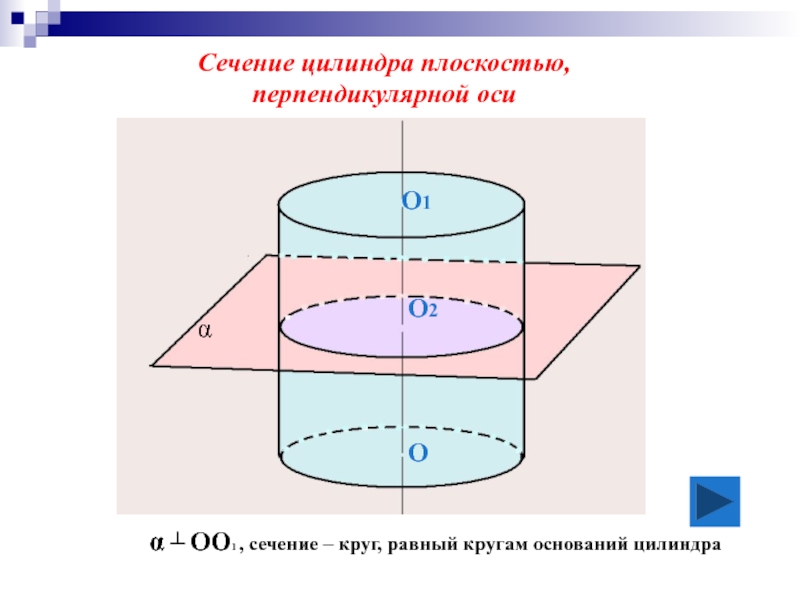
Слайд 12α ┴ OO1 , сечение – круг, равный кругам оснований цилиндра
Сечение
перпендикулярной оси
O
O1
O2
α
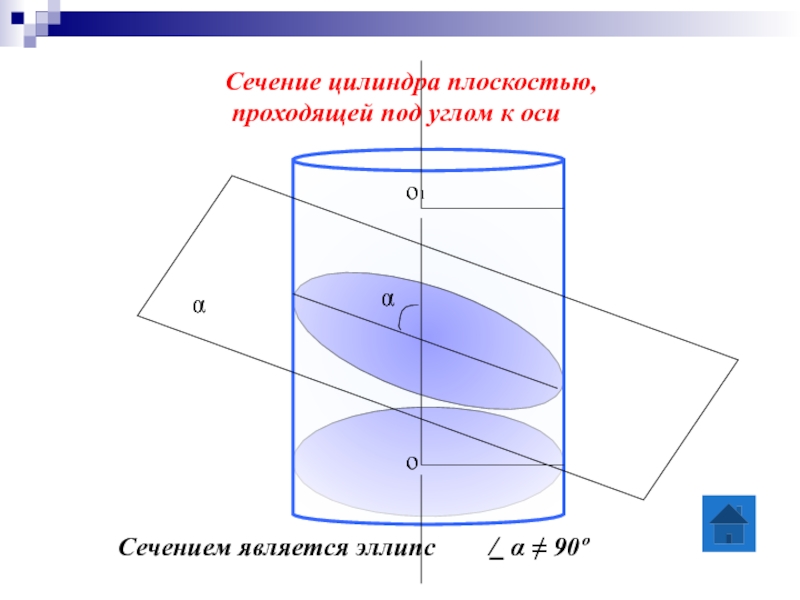
Слайд 13
Сечение цилиндра плоскостью,
проходящей под углом к оси
Сечением является эллипс
α
/
о
о1
α
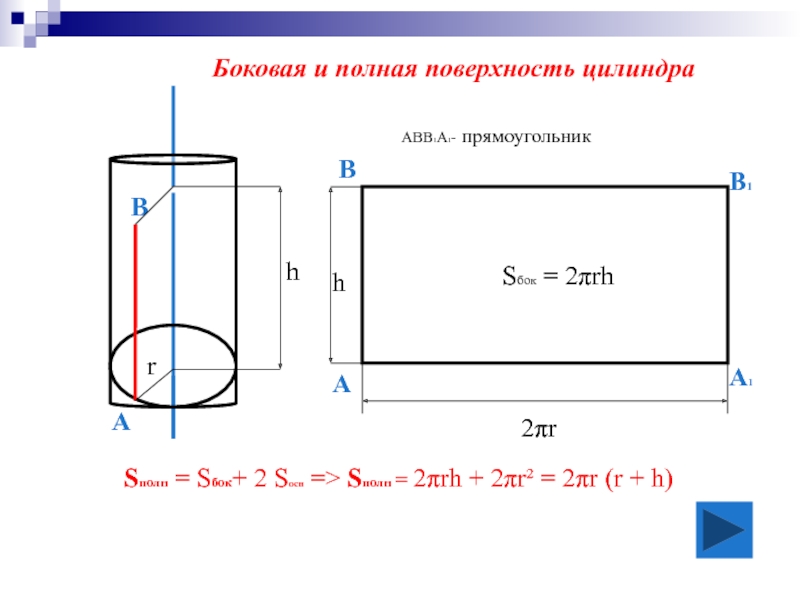
Слайд 14АВВ1А1- прямоугольник
В
А1
В1
А
2πr
h
Sбок = 2πrh
Sполн = Sбок+ 2 Sосн => Sполн =
Боковая и полная поверхность цилиндра
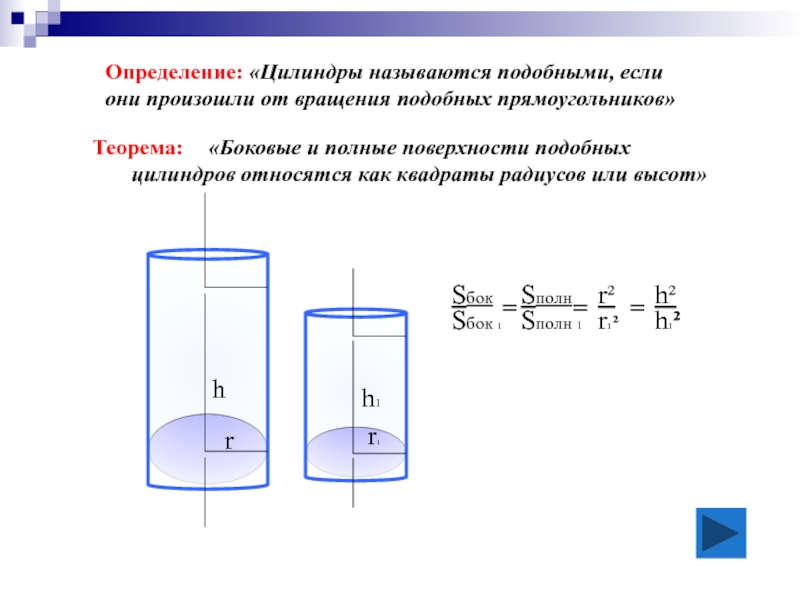
Слайд 15«Боковые и полные поверхности подобных
цилиндров относятся как квадраты радиусов или
Теорема:
Определение: «Цилиндры называются подобными, если
они произошли от вращения подобных прямоугольников»
Sбок 1
=
r1 ²
=
h1²
Sбок
r²
h²
=
Sполн
Sполн 1
Слайд 17Задача
Первый вариант
Вычислите полную и боковую
поверхность цилиндра,
радиус которого равен 3 м, а
(ответ дать, не вычисляя значения π )
Второй вариант
Вычислите полную и боковую
поверхность цилиндра,
радиус которого равен 2 дм, а высота 6 дм
(ответ дать, не вычисляя значения π )
Слайд 18Историческая справка
Слово «цилиндр» происходит от греческого
слова «ΚΙΛΙΝΔΡΟΣ»,
что означает «валик»,
Слайд 39Ответь на вопросы
1. Назови элементы цилиндра
2.Назови вид осевого сечения цилиндра
3. Может
прямоугольником
квадратом
трапецией?
4.Какие из данных утверждений верны:
любое сечение цилиндра плоскостью, перпендикулярной основанию есть окружность, равная окружности основания;
любое сечение цилиндра плоскостью есть окружность, равная окружности основания;
плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра;
сечением цилиндра могут быть круг, прямоугольник, эллипс.