Преподаватель математики
С. А. Осетрова
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие предела функции в точке. Теоремы о пределах презентация
Содержание
- 1. Понятие предела функции в точке. Теоремы о пределах
- 2. Предел функции Предел – одно из основных
- 3. Рассмотрим функции, графики которых изображены на следующих
- 4. Для функции график которой изображен на
- 5. Для функции график которой изображен на
- 6. Для функции график которой изображен на
- 7. Для всех трех случаев используется одна и
- 8. ТЕОРЕМА 1. Предел СУММЫ
- 9. ТЕОРЕМА 2. Предел константы равен самой этой константе.
- 10. ТЕОРЕМА 3. Предел ПРОИЗВЕДЕНИЯ
- 11. ТЕОРЕМА 4. Предел ОТНОШЕНИЯ
- 12. ТЕОРЕМА 5. Постоянный множитель можно выносить за знак предела
- 13. ТЕОРЕМА 6. Предел СТЕПЕНИ переменного равен той же степени предела основания:
- 14. Вычисление пределов Вычисление предела: начинают с подстановки
- 15. Домой (4 примера): 7 3 1 3 1,4
- 16. Часто при подстановке предельного значения x0 в
- 17. В большинстве случаев, чтобы раскрыть неопределенность вида
- 18. Пример №1: Разложим числитель и знаменатель на множители:
- 19. Вернемся к примеру 01.09.2016 0 -4 -1,5 Домой (№5,6,7):
- 20. Раскрытие неопределенностей Если f(x) – дробно
- 21. Упражнения (13 примеров):
- 22. Домашнее задание (№8-11): + знать ответы на
- 23. Дополнительно 01.09.2016
Слайд 1Понятие предела функции в точке. Теоремы о пределах
СГБОУ ПО «СМК имени
Жени Дерюгиной»
Слайд 2Предел функции
Предел – одно из основных понятий математического анализа. Понятие предела
использовалось еще Ньютоном во второй половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела дали Больцано в 1816 году и Коши в 1821 году.
РАЗЛИЧАЮТ – предел функции в точке И предел функции на бесконечности.
Ньютон
Эйлер
Лагранж
Больцано
Коши
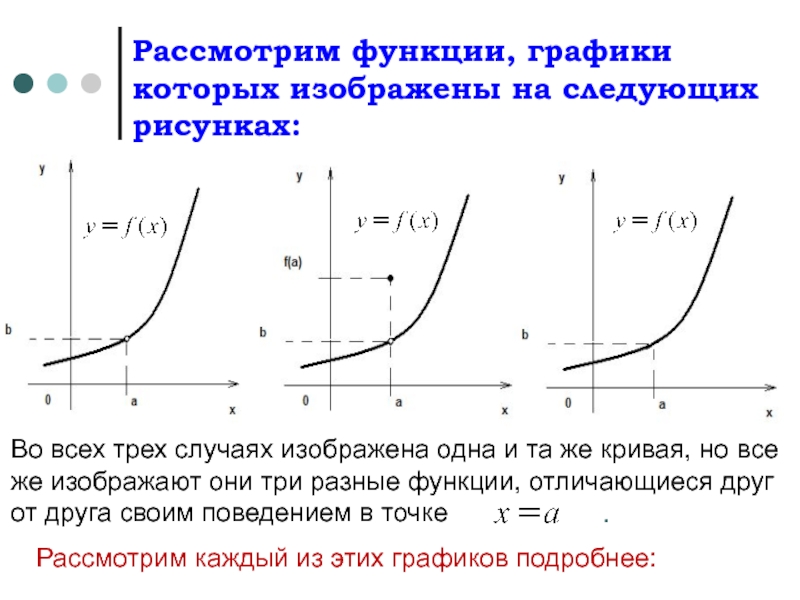
Слайд 3Рассмотрим функции, графики которых изображены на следующих рисунках:
Во всех трех случаях
изображена одна и та же кривая, но все же изображают они три разные функции, отличающиеся друг от друга своим поведением в точке
.
Рассмотрим каждый из этих графиков подробнее:
Слайд 4
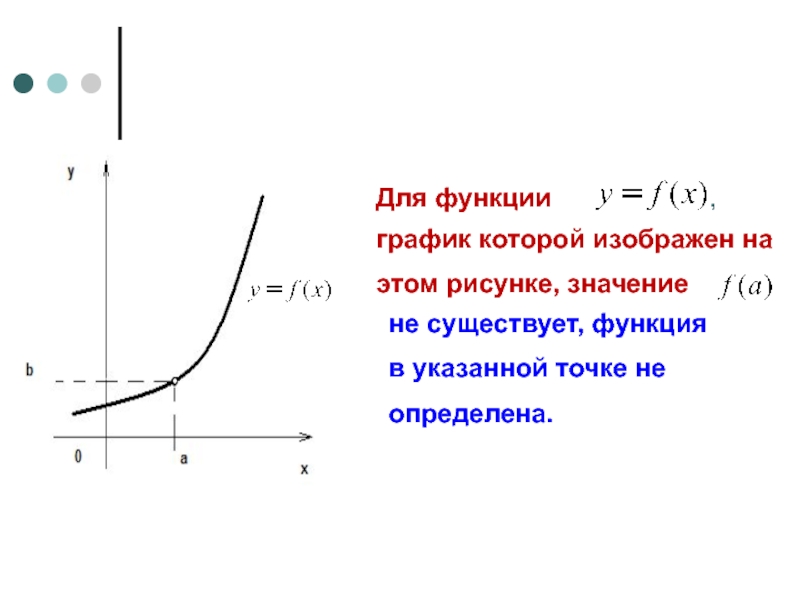
Для функции
график которой изображен на
этом рисунке, значение
,
не существует, функция
в
указанной точке не
определена.
определена.
Слайд 5
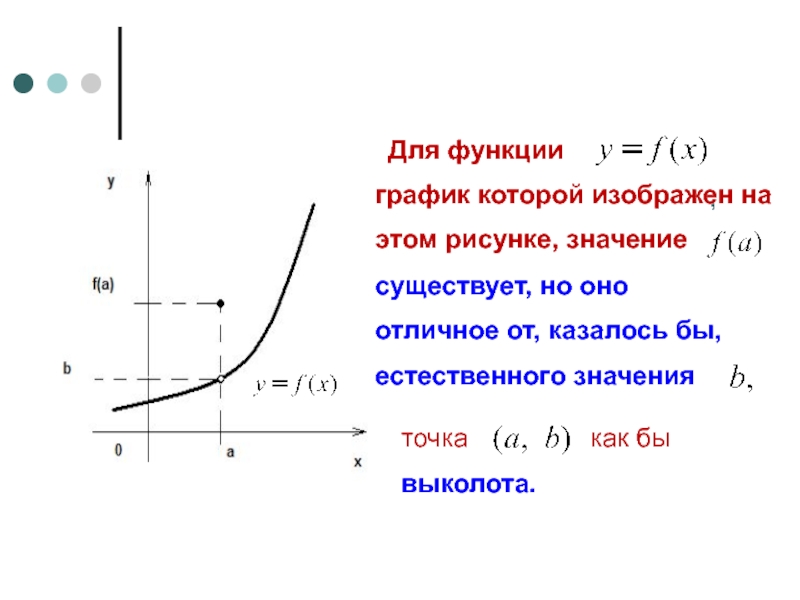
Для функции
график которой изображен на
этом рисунке, значение
,
существует, но оно
отличное
от, казалось бы,
естественного значения
естественного значения
точка
как бы
выколота.
Слайд 6
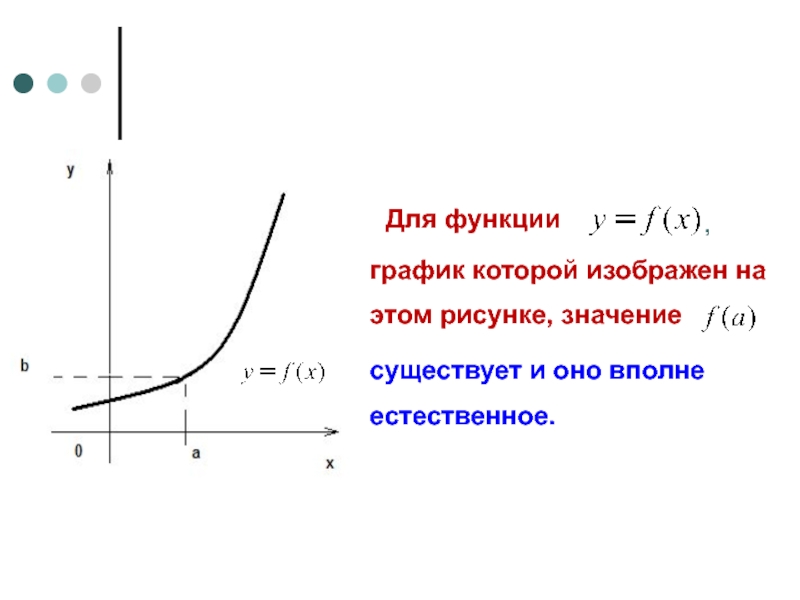
Для функции
график которой изображен на
этом рисунке, значение
,
существует и оно вполне
естественное.
Слайд 7Для всех трех случаев используется одна и та же запись:
которую читают:
«предел функции
при
стремлении
к равен ».
Опр. Число называется пределом функции в точке а, если для всех значений х, достаточно близких к а и отличных от а, значение функции
f (x) сколь угодно мало отличается
от .
Слайд 8ТЕОРЕМА 1.
Предел СУММЫ (разности) 2-х функций равен СУММЕ (разности) их
пределов, если последние существуют:
Слайд 10ТЕОРЕМА 3.
Предел ПРОИЗВЕДЕНИЯ 2-х функций равен ПРОИЗВЕДЕНИЮ их пределов, если
последние существуют:
Слайд 11ТЕОРЕМА 4.
Предел ОТНОШЕНИЯ 2-х функций равен ОТНОШЕНИЮ их пределов, если
последние существуют и ПРЕДЕЛ ЗНАМЕНАТЕЛЯ ОТЛИЧЕН ОТ 0:
Слайд 14Вычисление пределов
Вычисление предела:
начинают с подстановки предельного значения x0 в функцию f(x).
Если
при этом получается конечное число, то предел равен этому числу.
Если при подстановки предельного значения x0 в функцию f(x) получаются выражения вида:
то предел будет равен:
Слайд 16Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения
следующих видов:
Эти выражения называются неопределенности, а вычисление пределов в этом случае называется раскрытие неопределенности.
Слайд 17В большинстве случаев, чтобы раскрыть неопределенность вида ,
достаточно
числитель и знаменатель дроби разложить на множители, и затем сократить на множитель, приводящий к неопределенности.
числитель и знаменатель дроби разложить на множители, и затем сократить на множитель, приводящий к неопределенности.
Правило № 1
Слайд 20Раскрытие неопределенностей
Если f(x) – дробно – рациональная функция, необходимо разложить на
множители числитель и знаменатель дроби
Если f(x) – иррациональная дробь, необходимо умножить числитель и знаменатель дроби на выражение, сопряженное числителю.
Слайд 22Домашнее задание (№8-11):
+ знать ответы на следующие вопросы:
С какими математиками связано
понятие «Предел»?
Как вычислить предел?
Как раскрыть неопределенность вида 0/0?
Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
Уметь формулировать теоремы.
Как вычислить предел?
Как раскрыть неопределенность вида 0/0?
Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
Уметь формулировать теоремы.
