- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие логарифма. Свойства логарифма презентация
Содержание
- 1. Понятие логарифма. Свойства логарифма
- 2. Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас Для чего были придуманы логарифмы?
- 3. Цели урока Ввести понятие «логарифм числа». Рассмотреть
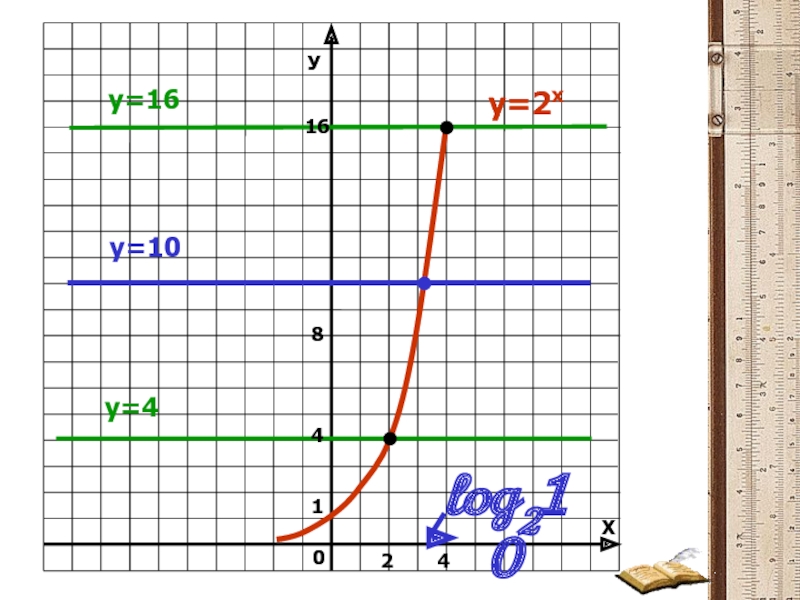
- 4. y=2x 8 2 4
- 5. Термин «логарифм» возник из сочетания греческих
- 6. Найдите : Log28= Log12144= Log464= Log381= Log749=
- 7. Определение логарифма Логарифмом числа 8 по основанию
- 8. Определение логарифма Логарифмом числа b по основанию
- 9. Свойства, следующие из определения logaa=1 loga1=0 logaac=c
- 10. Найдите ошибку: Log2(-8)=3 Log(-12)144=2 Log11=1 7Log749=2 Log416=4
- 11. Прологарифмируйте : Log28= Lоg10100= 4Log464= Log31= Log232=
- 12. Десятичным называется логарифм, основание которого
- 13. Десятичный логарифм Натуральный логарифм Примеры: lg10=1,
- 14. Логарифмические таблицы
- 15. Титульный лист книги Дж. Непера «Описание удивительной таблицы логарифмов». Издание 1620 г.
- 17. Логарифмические палочки
- 20. Гунтер – изобретатель логарифмической линейки Через десяток
- 21. У инженера и астронома не было инструмента полезнее, чем логарифмическая линейка.
- 26. Итог урока Что называют логарифмом положительного
- 27. Домашнее задание. Если со всеми предложенными заданиями
- 28. « СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС,
- 29. Спасибо за внимание
Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас Для чего были придуманы логарифмы?
Слайд 2Изобретение логарифмов, сократив работу астронома, продлило ему жизнь.
П.С. Лаплас
Для чего были
придуманы логарифмы?
Слайд 3Цели урока
Ввести понятие «логарифм числа».
Рассмотреть свойства логарифмов.
Познакомиться с историей возникновения
логарифмов.
Слайд 5 Термин «логарифм» возник из сочетания греческих слов λόγος (logos) -отношение,
соотношение и ἀριθμός (arithmos) - число.
«отношение чисел».
«отношение чисел».
log21=0, log22=1, log24=2, log28=3
1,2,4,8…-геометрическая прогрессия,
0,1,2,3…-арифметическая прогрессия.
log21=0, log22=1, log24=2, log28=3
Слайд 6Найдите :
Log28=
Log12144=
Log464=
Log381=
Log749=
Log232=
Log981=
Log327=
Log5125=
Log636=
Log216=
Log10100=
3
3
4
4
2
2
2
2
3
3
2
5
Log24=
Log33=
Log31=
Log525=
Log66=
Log101=
0
1
2
0
1
2
Слайд 7Определение логарифма
Логарифмом числа 8 по основанию 2 называется показатель степени, в
которую нужно возвести число 2, чтобы получить число 8
log28=3
23=8
ax=b
logab=x
a >0 a≠1
b>0
a >0 a≠1
b>0
Слайд 8Определение логарифма
Логарифмом числа b по основанию a называется показатель степени, в
которую нужно возвести число a, чтобы получить число b ( а>0, a≠1, b>0)
logab
a
=b
Основное логарифмическое тождество
Слайд 10Найдите ошибку:
Log2(-8)=3
Log(-12)144=2
Log11=1
7Log749=2
Log416=4
9Log9(-9)=-1
1Log749=2
1Log749=1
2
Log40=4
5Log55=1
2
2
Слайд 11Прологарифмируйте :
Log28=
Lоg10100=
4Log464=
Log31=
Log232=
Log981=
Lоg101000=
5Log525=
Log61=
Log216=
3
64
4
0
2
0
25
3
2
5
Вариант 1
Вариант 2
Слайд 12
Десятичным называется логарифм, основание которого равно 10. Обозначается lg b, т.е.
lg b=log10 b.
Натуральным называется логарифм, основание которого равно e. Обозначается ln b, т.е. ln b=loge b.
Натуральным называется логарифм, основание которого равно e. Обозначается ln b, т.е. ln b=loge b.
Слайд 13Десятичный логарифм
Натуральный логарифм
Примеры:
lg10=1,
lg1=0,
lg0,01=-2.
log10 → lg
е ≈ 2,718281828…
loge
→ ln
Примеры:
ln e=1,
ln1=0,
ln e2=2.
Слайд 20Гунтер – изобретатель логарифмической линейки
Через десяток лет после появления логарифмов Непера
английский ученый Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку.
Без логарифмической линейки не были бы построены ни первые компьютеры, ни микрокалькуляторы.
Слайд 26Итог урока
Что называют логарифмом положительного числа b по основанию a
(a>0, a≠1)?
Существует ли логарифм нуля; логарифм отрицательного числа?
Существует ли логарифм нуля; логарифм отрицательного числа?
Слайд 27Домашнее задание.
Если со всеми предложенными заданиями Вы справились без ошибок, то
Ваше домашнее задание: п.37, № 489, № 490, № № 495(b,в), №496(b,в,г).
Если при выполнении предложенных заданий Вы испытывали затруднения и не смогли всё вы-полнить правильно, то Ваше домашнее зада-ние: п.37, № 476, № 483(b,в), № 488, № 495(b,в).
Слайд 28« СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС, В КОТОРЫЙ ТЫ НЕ
УСВОИЛ НИЧЕГО НОВОГО И НИЧЕГО НЕ ПРИ-БАВИЛ К СВОЕМУ ОБРАЗОВАНИЮ.»
Я. А. КОМЕНСКИЙ.
