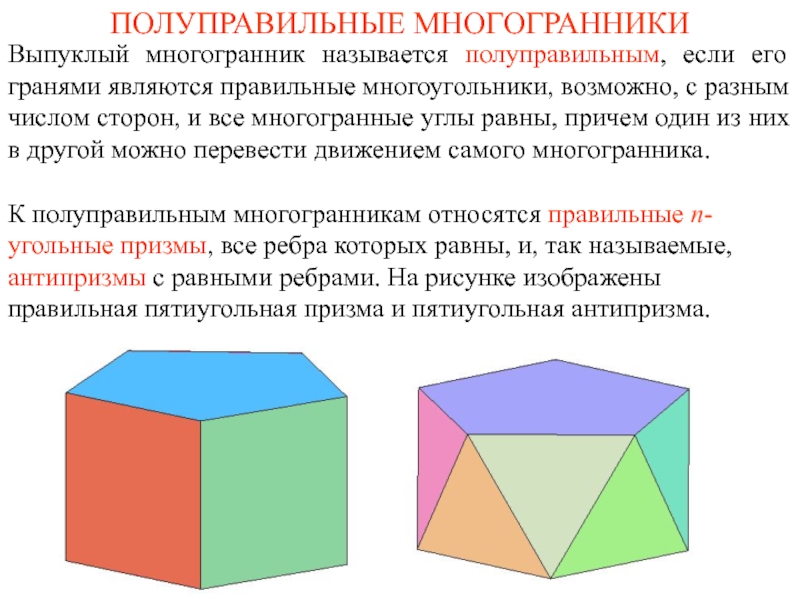
Выпуклый многогранник называется полуправильным, если его гранями являются правильные многоугольники, возможно, с разным числом сторон, и все многогранные углы равны, причем один из них в другой можно перевести движением самого многогранника.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Полуправильные многогранники презентация
Содержание
- 1. Полуправильные многогранники
- 2. ТЕЛА АРХИМЕДА Кроме этих двух бесконечных серий
- 3. Усеченный тетраэдр Кроме этих двух бесконечных серий
- 4. Усеченный куб Какую часть ребер нужно отсекать
- 5. Усеченный октаэдр Какую часть ребер нужно отсекать
- 6. Усеченный икосаэдр Какую часть ребер нужно отсекать
- 7. Усеченный додекаэдр Какую часть ребер нужно отсекать
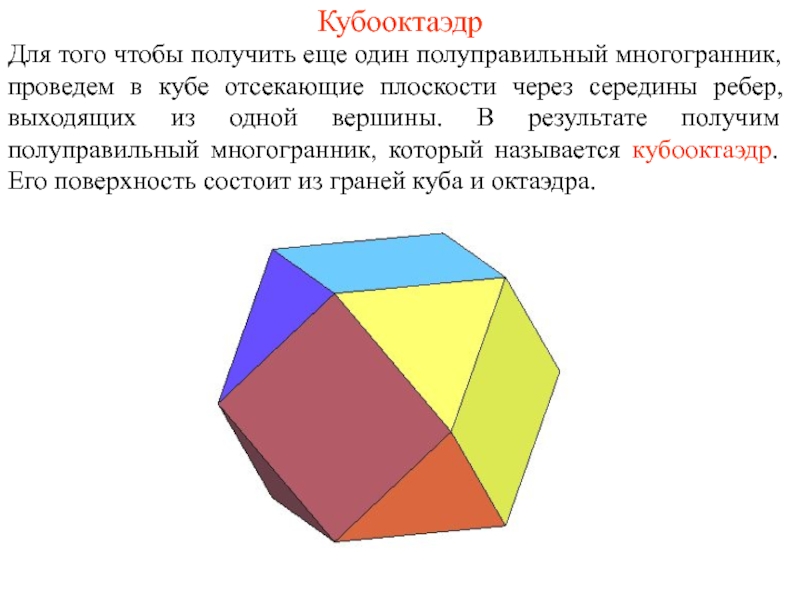
- 8. Кубооктаэдр Для того чтобы получить еще один
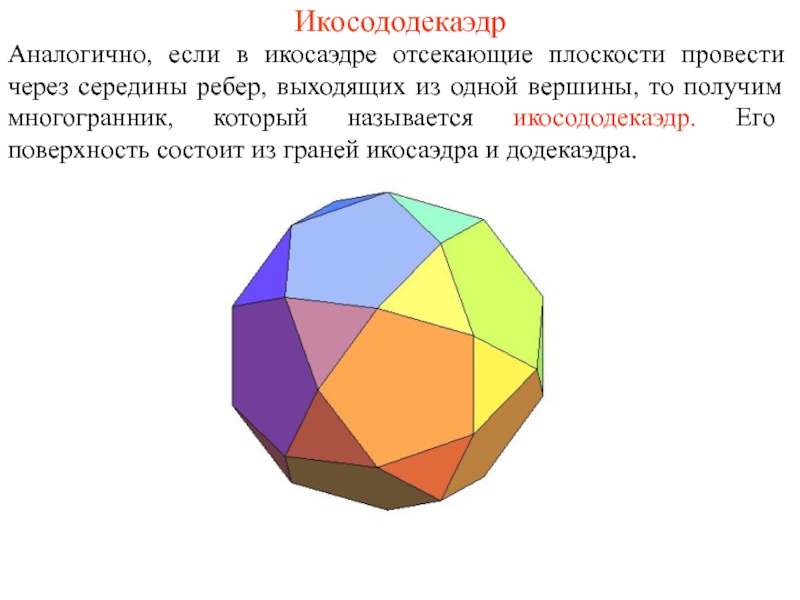
- 9. Икосододекаэдр Аналогично, если в икосаэдре отсекающие плоскости
- 10. Упражнение 1 Какой многогранник получится, если в
- 11. Упражнение 2 Какой многогранник получится, если в
- 12. Упражнение 3 Какой многогранник получится, если в
- 13. Усеченный кубооктаэдр Полуправильный многогранник, изображенный на рисунке
- 14. Усеченный икосододекаэдр Полуправильный многогранник, изображенный на рисунке
- 15. Ромбокубооктаэдр На рисунке изображен многогранник, называемый ромбокубооктаэдр.
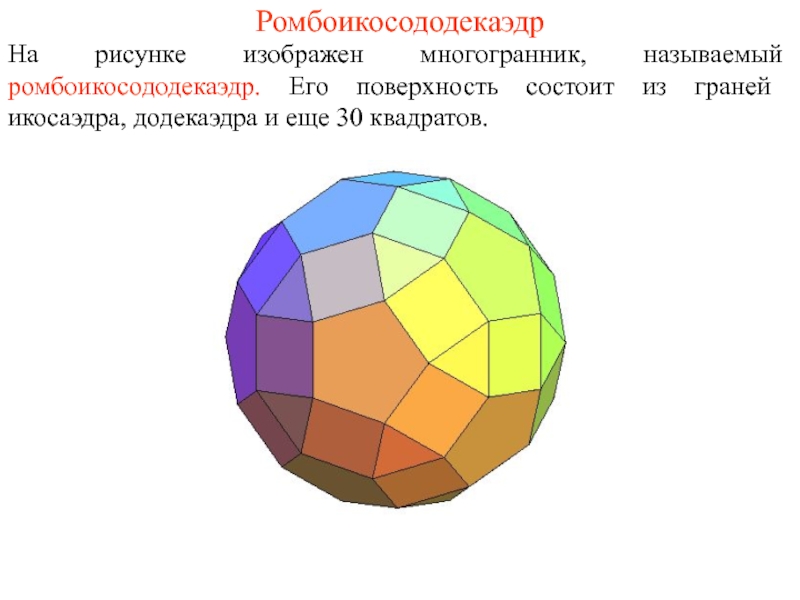
- 16. Ромбоикосододекаэдр На рисунке изображен многогранник, называемый ромбоикосододекаэдр.
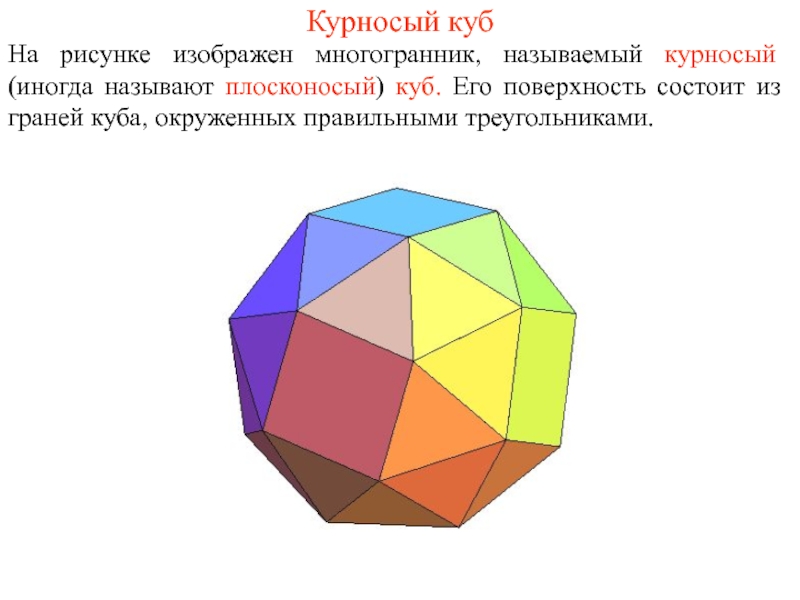
- 17. Курносый куб На рисунке изображен многогранник, называемый
- 18. Курносый додекаэдр Последний многогранник Архимеда называется курносый
- 19. Упражнение 4 Из каких граней состоит усеченный
- 20. Упражнение 5 Из каких граней состоит усеченный
- 21. Упражнение 6 Из каких граней состоит усеченный
- 22. Упражнение 7 Ребро куба равно 1. Найдите ребро полученного из него усеченного куба.
- 23. Упражнение 8 Из каких граней состоит усеченный
- 24. Упражнение 9 Ребро додекаэдра равно 1. Найдите ребро полученного из него усеченного додекаэдра.
- 25. Упражнение 10 Из каких граней состоит усеченный
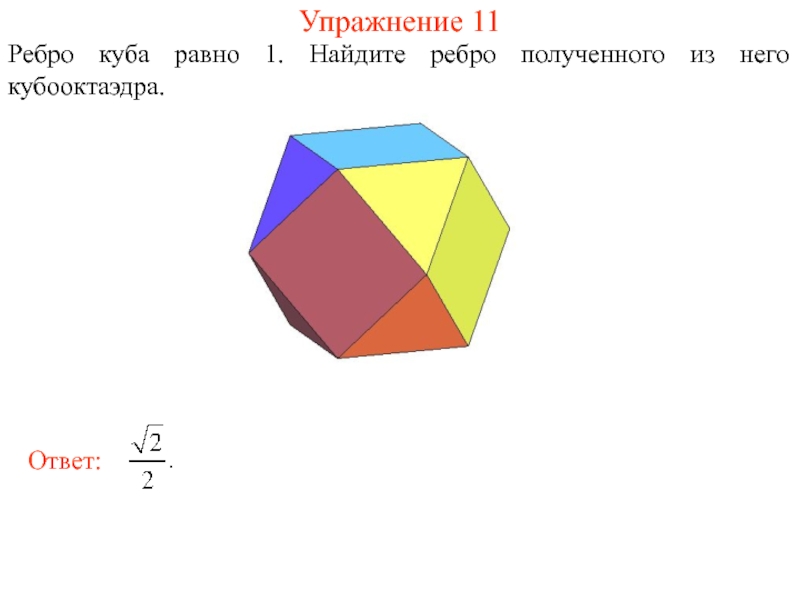
- 26. Упражнение 11 Ребро куба равно 1. Найдите ребро полученного из него кубооктаэдра.
- 27. Упражнение 12 Из каких граней состоит кубооктаэдр?
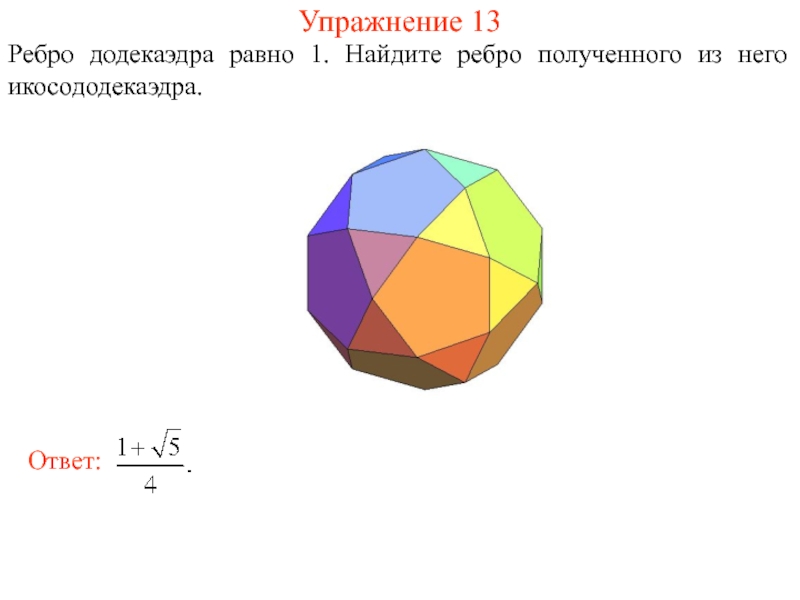
- 28. Упражнение 13 Ребро додекаэдра равно 1. Найдите ребро полученного из него икосододекаэдра.
- 29. Упражнение 14 Из каких граней состоит икосододекаэдр?
- 30. Упражнение 15 Из каких граней состоит усеченный
- 31. Упражнение 16 Из каких граней состоит усеченный
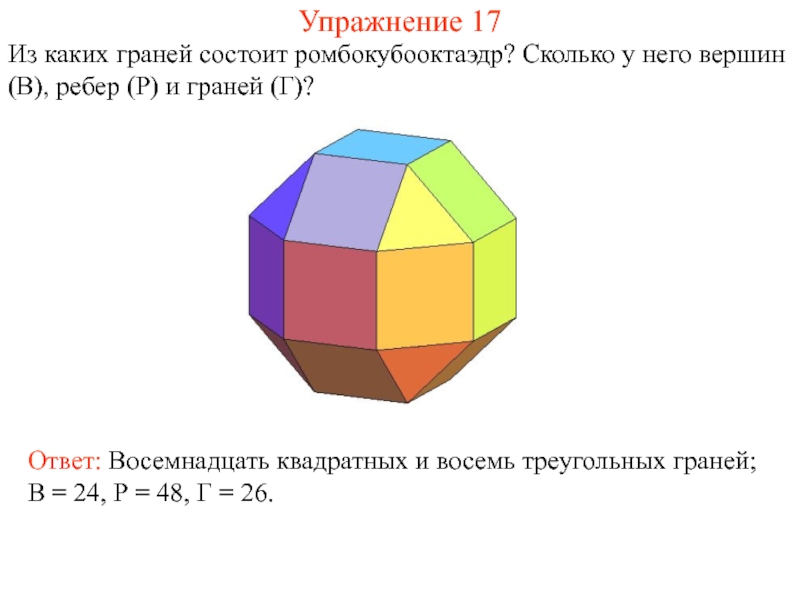
- 32. Упражнение 17 Из каких граней состоит ромбокубооктаэдр?
- 33. Упражнение 18 Из каких граней состоит ромбоикосододекаэдр?
- 34. Упражнение 19 Из каких граней состоит курносый
- 35. Упражнение 20 Из каких граней состоит курносый
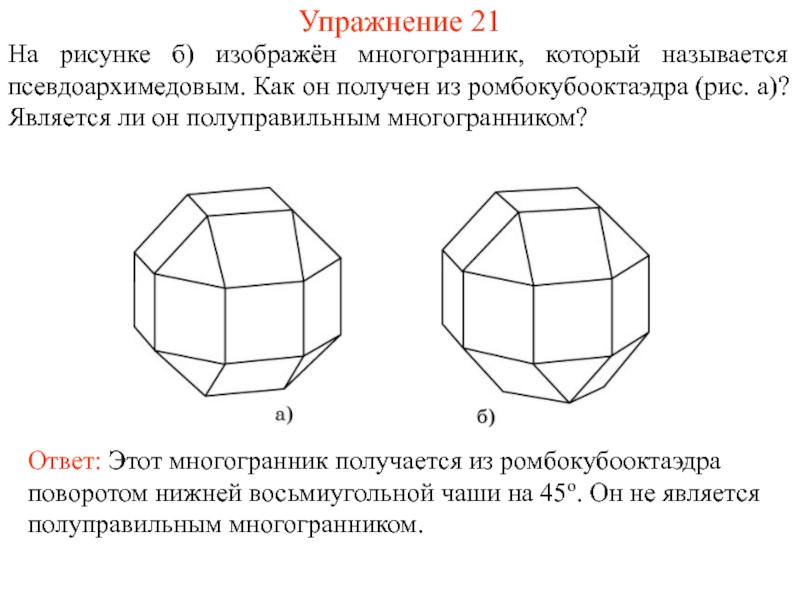
- 36. Упражнение 21 На рисунке б) изображён многогранник,
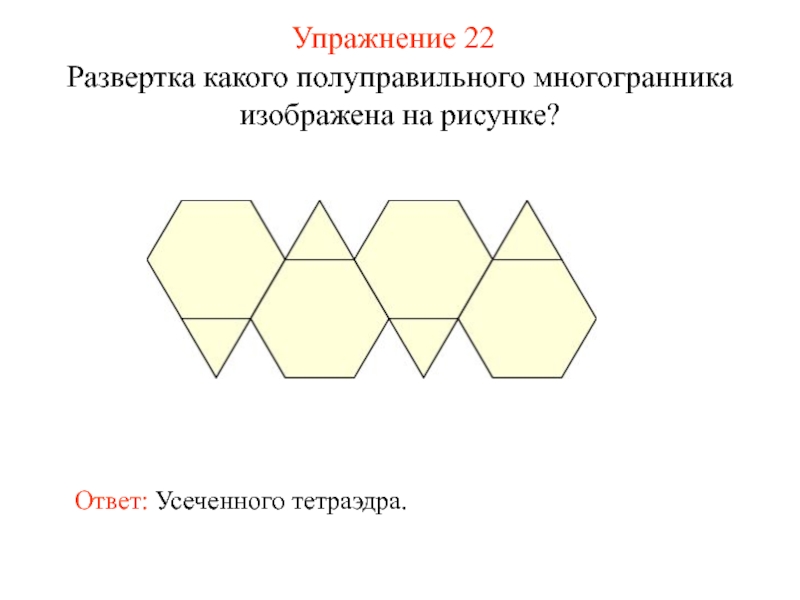
- 37. Упражнение 22 Развертка какого полуправильного многогранника изображена на рисунке? Ответ: Усеченного тетраэдра.
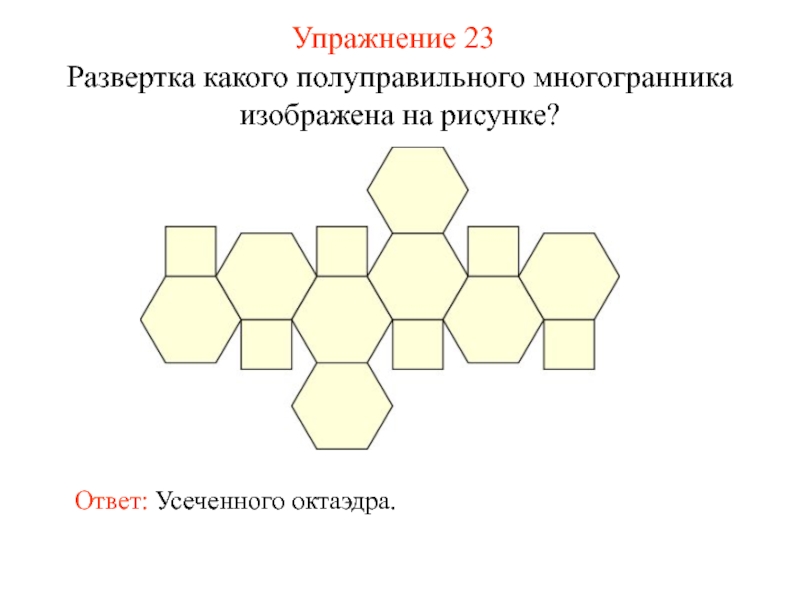
- 38. Упражнение 23 Развертка какого полуправильного многогранника изображена на рисунке? Ответ: Усеченного октаэдра.
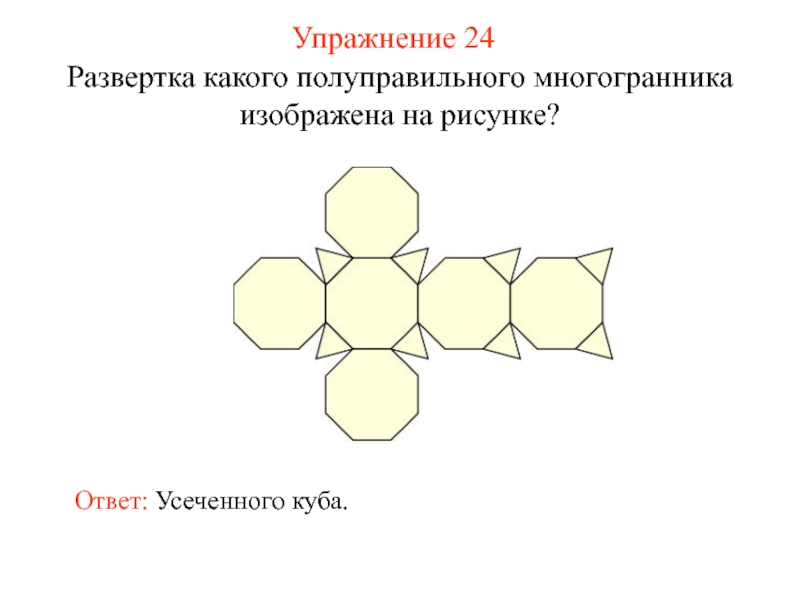
- 39. Упражнение 24 Развертка какого полуправильного многогранника изображена на рисунке? Ответ: Усеченного куба.
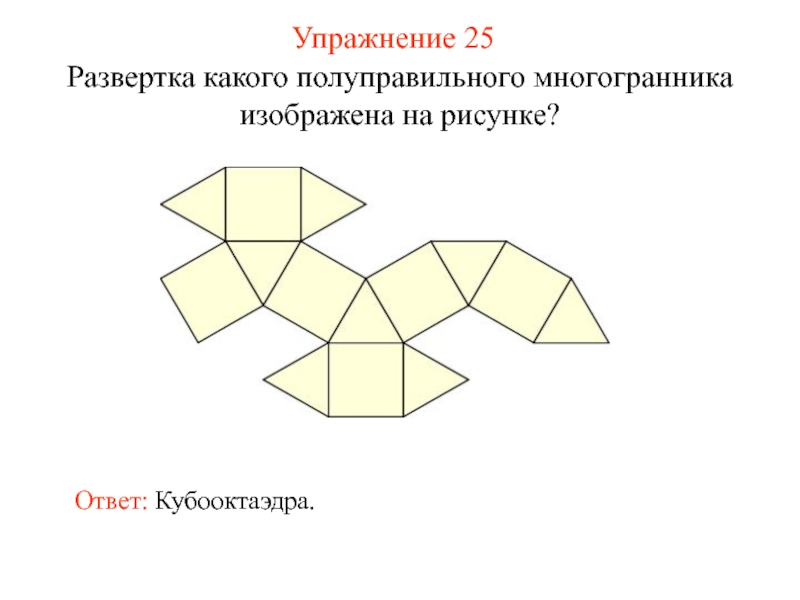
- 40. Упражнение 25 Развертка какого полуправильного многогранника изображена на рисунке? Ответ: Кубооктаэдра.
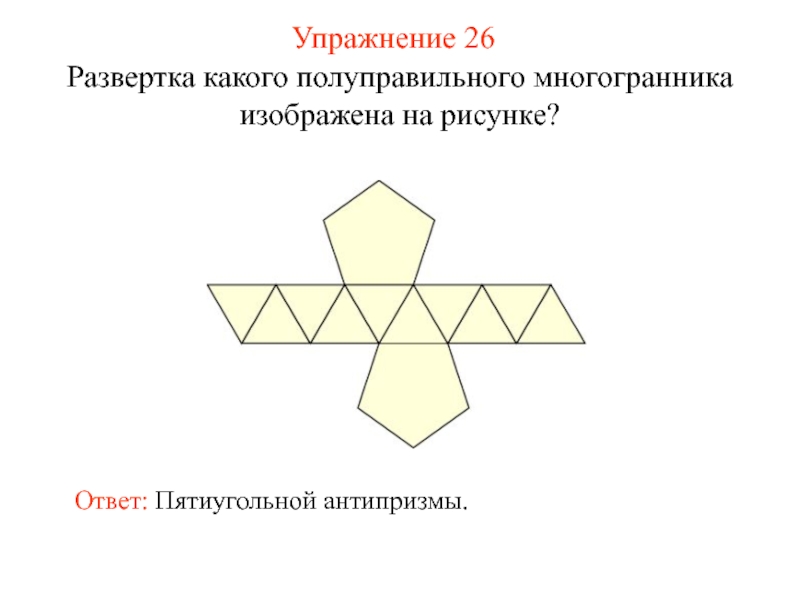
- 41. Упражнение 26 Развертка какого полуправильного многогранника изображена на рисунке? Ответ: Пятиугольной антипризмы.
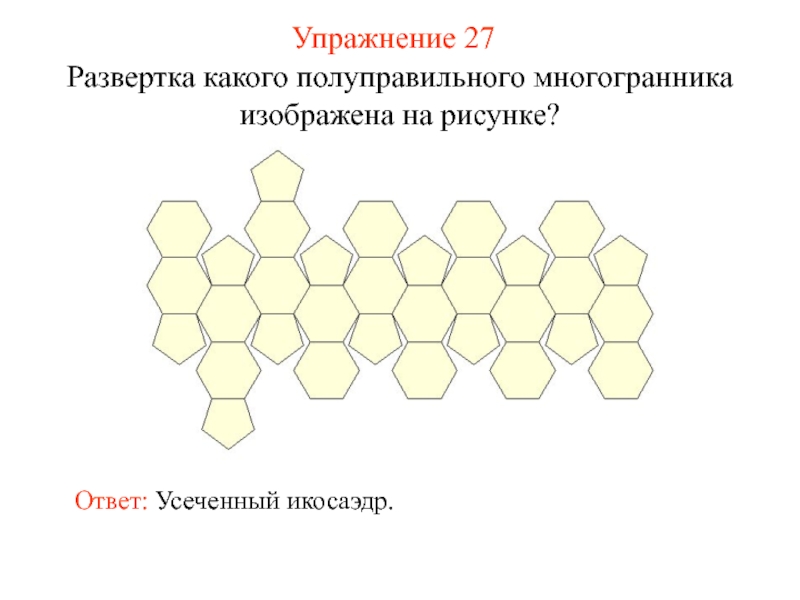
- 42. Упражнение 27 Развертка какого полуправильного многогранника изображена на рисунке? Ответ: Усеченный икосаэдр.
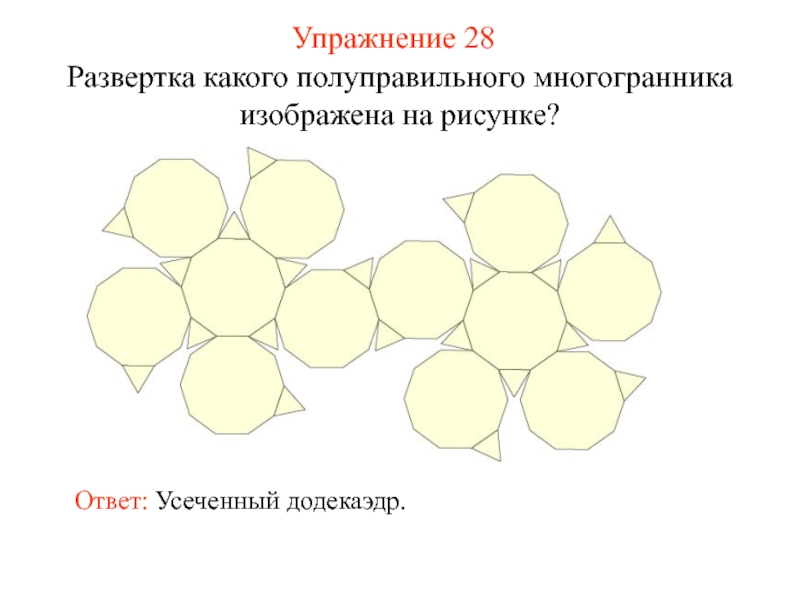
- 43. Упражнение 28 Развертка какого полуправильного многогранника изображена на рисунке? Ответ: Усеченный додекаэдр.
- 44. Упражнение 29 Развертка какого полуправильного многогранника изображена на рисунке? Ответ: Икосододекаэдр.
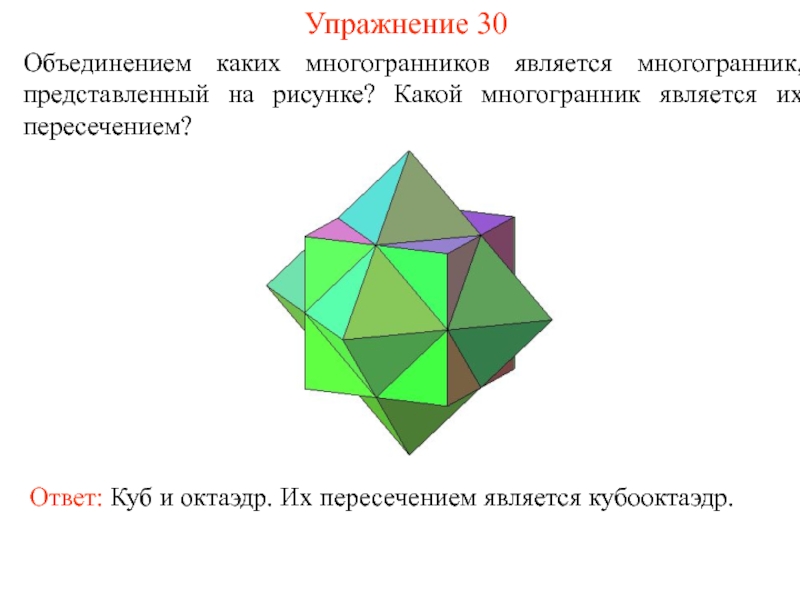
- 45. Упражнение 30 Объединением каких многогранников является многогранник,
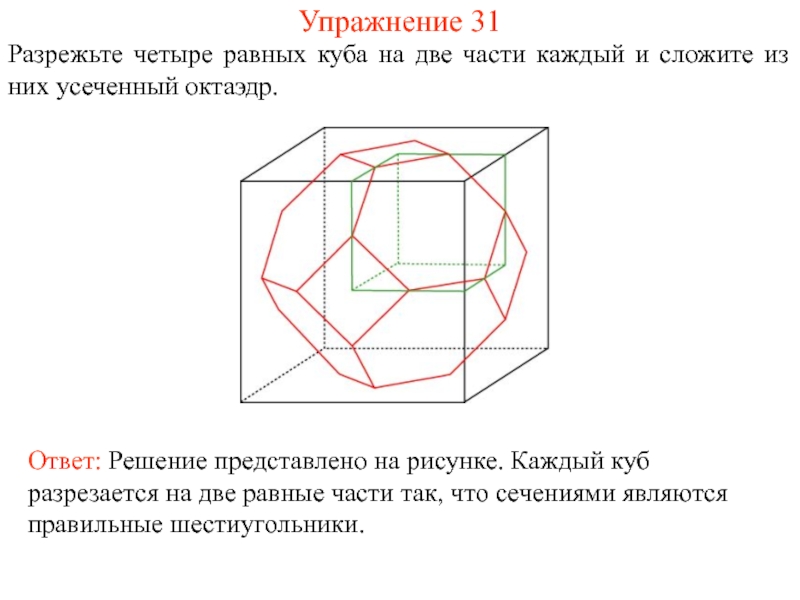
- 46. Упражнение 31 Разрежьте четыре равных куба на
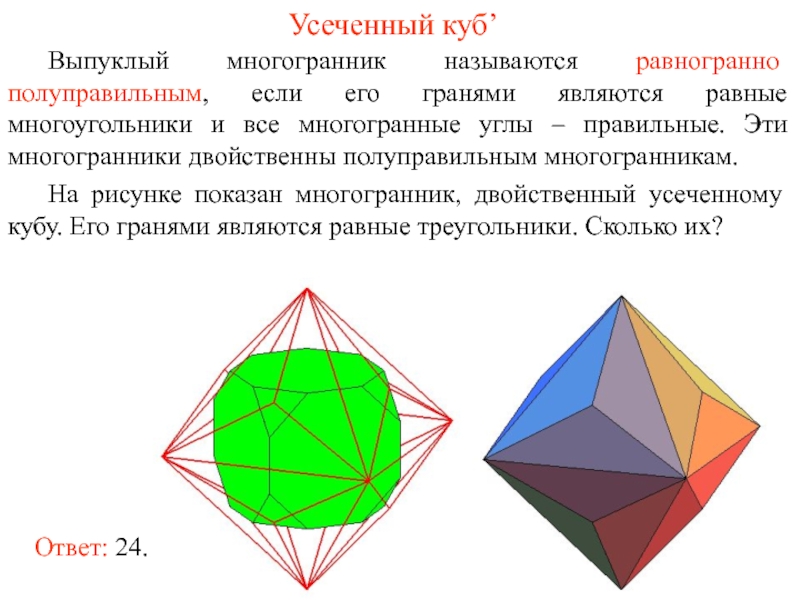
- 47. Усеченный куб’ Выпуклый многогранник называются равногранно полуправильным,
- 48. Усеченный тетраэдр’ На рисунке показан многогранник, двойственный
- 49. Усеченный октаэдр’ На рисунке показан многогранник, двойственный
- 50. Усеченный икосаэдр’ На рисунке показан многогранник, двойственный
- 51. Усеченный додекаэдр’ На рисунке показан многогранник, двойственный усеченному додекаэдру. Его гранями являются равные треугольники.
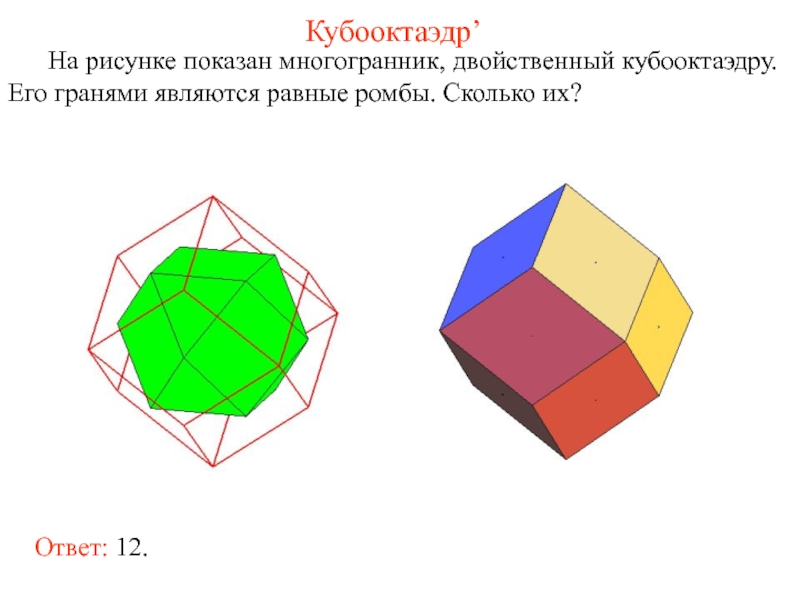
- 52. Кубооктаэдр’ На рисунке показан многогранник, двойственный кубооктаэдру.
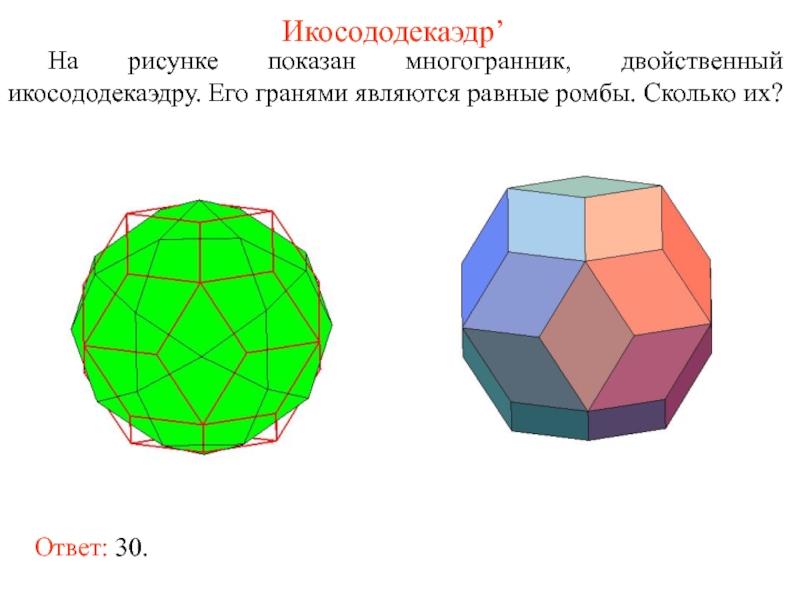
- 53. Икосододекаэдр’ На рисунке показан многогранник, двойственный икосододекаэдру.
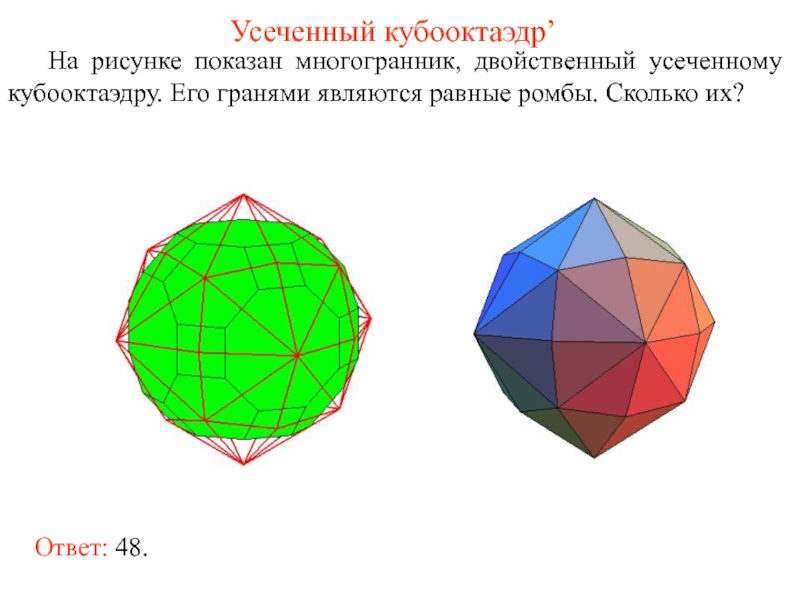
- 54. Усеченный кубооктаэдр’ На рисунке показан многогранник, двойственный
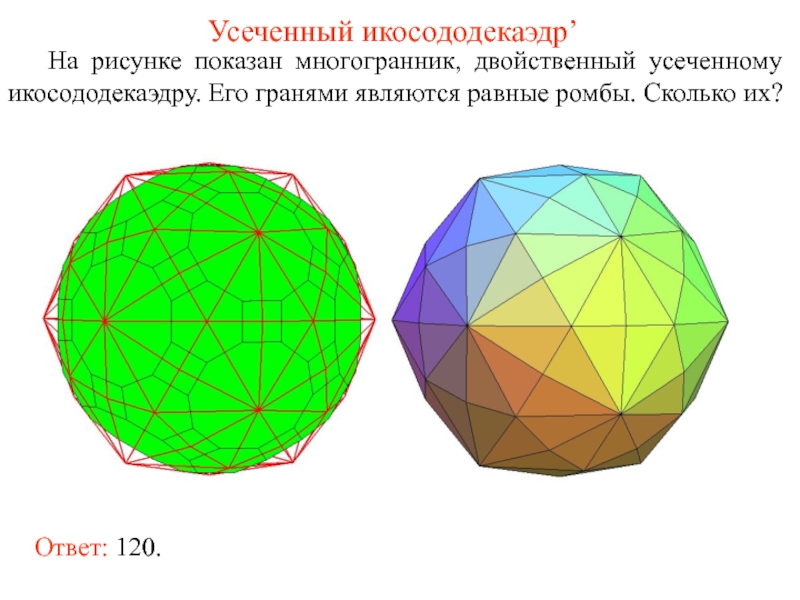
- 55. Усеченный икосододекаэдр’ На рисунке показан многогранник, двойственный
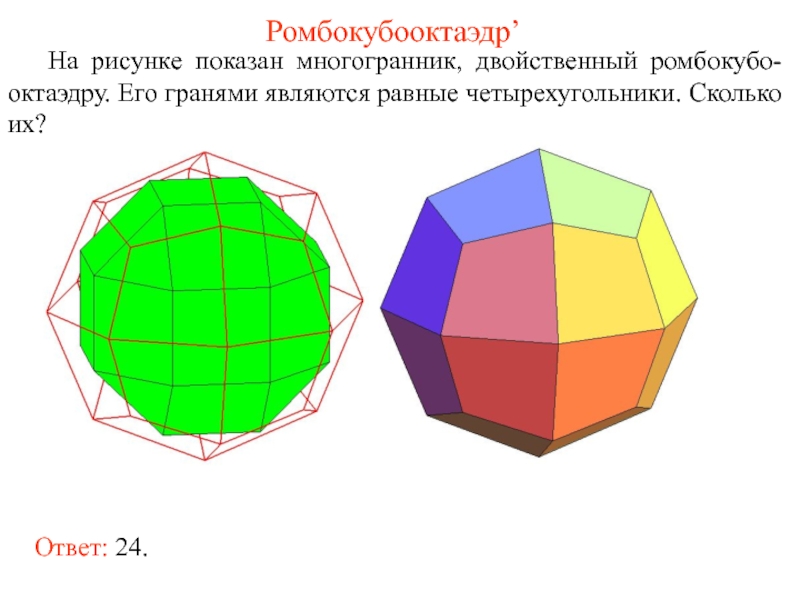
- 56. Ромбокубооктаэдр’ На рисунке показан многогранник, двойственный ромбокубо-октаэдру.
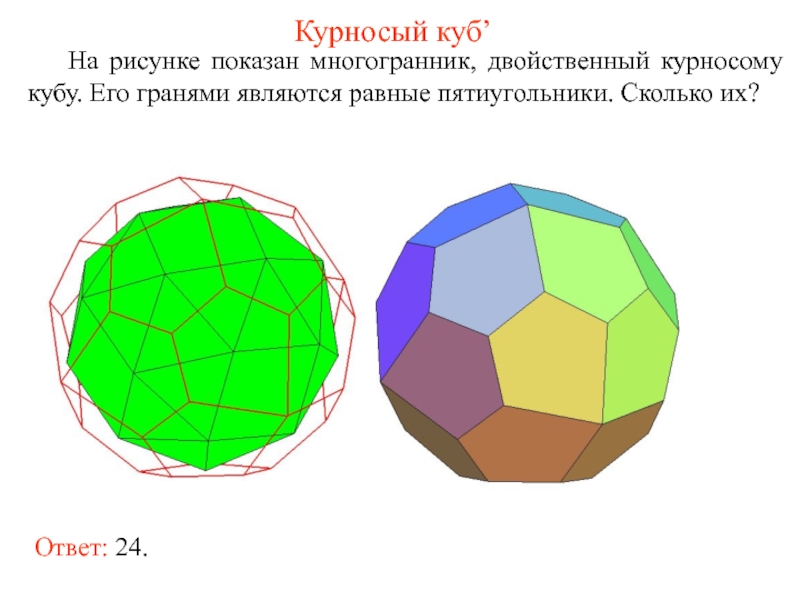
- 57. Курносый куб’ На рисунке показан многогранник, двойственный
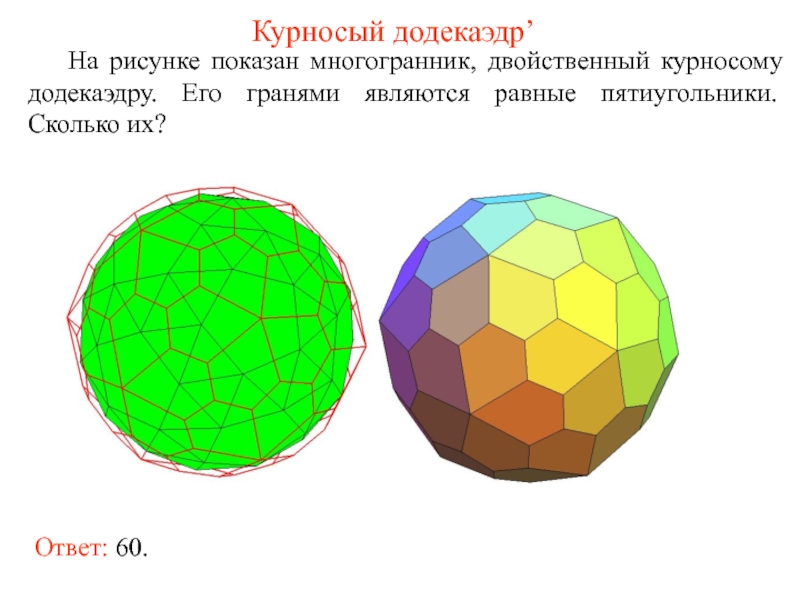
- 58. Курносый додекаэдр’ На рисунке показан многогранник, двойственный
ТЕЛА АРХИМЕДА Кроме этих двух бесконечных серий полуправильных многогранников, имеется еще 13 полуправильных многогранников, которые впервые открыл и описал Архимед (287 – 212 гг. до н. э.) - это тела Архимеда.
Слайд 1ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
К полуправильным многогранникам относятся правильные n-угольные призмы, все ребра которых
равны, и, так называемые, антипризмы с равными ребрами. На рисунке изображены правильная пятиугольная призма и пятиугольная антипризма.
Слайд 2ТЕЛА АРХИМЕДА
Кроме этих двух бесконечных серий полуправильных многогранников, имеется еще 13
полуправильных многогранников, которые впервые открыл и описал Архимед (287 – 212 гг. до н. э.) - это тела Архимеда.
Областью интересов Архимеда была не только математика, но и физика, оптика, астрономия и др. Он был изобретателем многих машин и механизмов, дошедших до наших дней.С помощью изобретенного им метода исчерпывания он вычислил длину окружности и получил приближения числа π,
Он вычислил площадь круга, объем и площадь поверхности шара и мн. др.
Цилиндр с вписанным в него шаром изображены на его надгробном камне в Сиракузах.
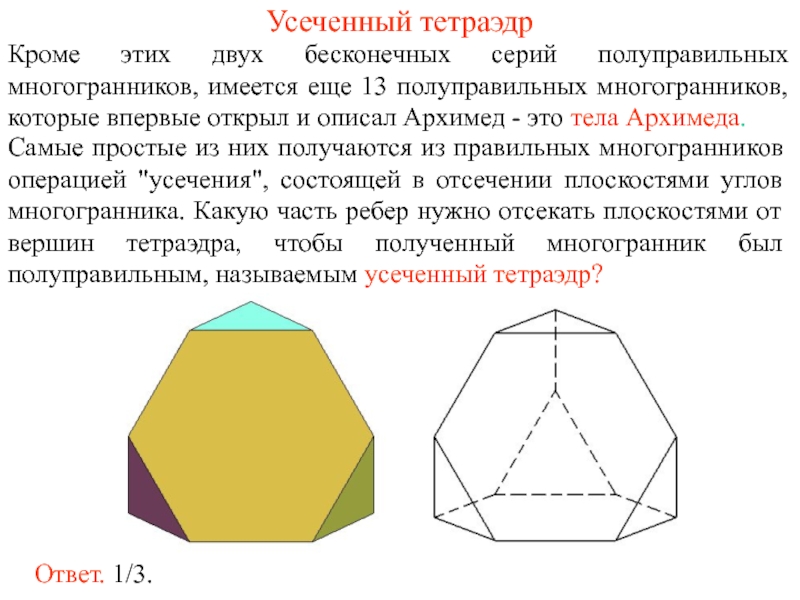
Слайд 3Усеченный тетраэдр
Кроме этих двух бесконечных серий полуправильных многогранников, имеется еще 13
полуправильных многогранников, которые впервые открыл и описал Архимед - это тела Архимеда.
Самые простые из них получаются из правильных многогранников операцией "усечения", состоящей в отсечении плоскостями углов многогранника. Какую часть ребер нужно отсекать плоскостями от вершин тетраэдра, чтобы полученный многогранник был полуправильным, называемым усеченный тетраэдр?
Ответ. 1/3.
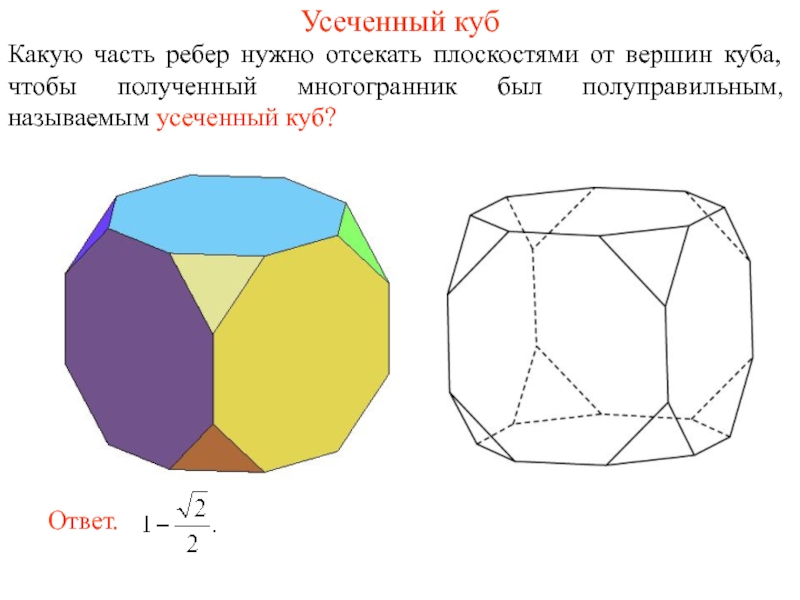
Слайд 4Усеченный куб
Какую часть ребер нужно отсекать плоскостями от вершин куба, чтобы
полученный многогранник был полуправильным, называемым усеченный куб?
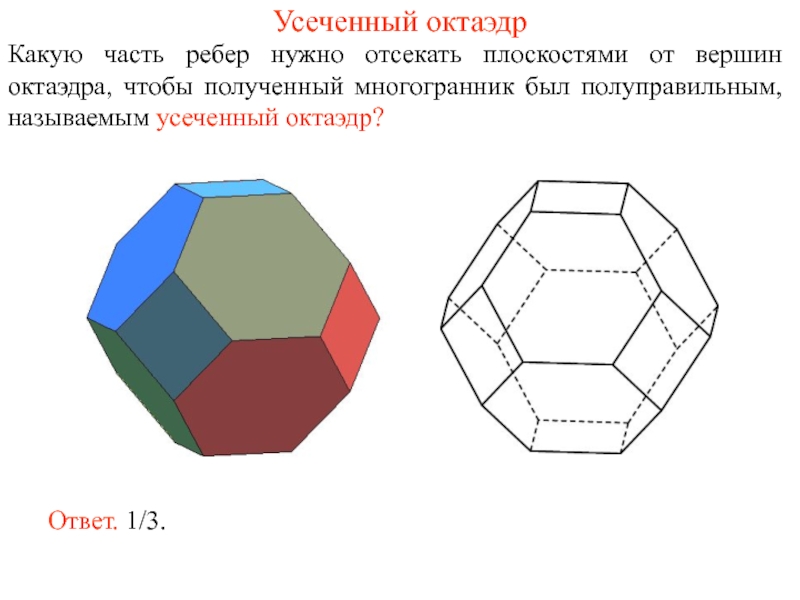
Слайд 5Усеченный октаэдр
Какую часть ребер нужно отсекать плоскостями от вершин октаэдра, чтобы
полученный многогранник был полуправильным, называемым усеченный октаэдр?
Ответ. 1/3.
Слайд 6Усеченный икосаэдр
Какую часть ребер нужно отсекать плоскостями от вершин икосаэдра, чтобы
полученный многогранник был полуправильным, называемым усеченный икосаэдр? Обратите внимание на то, что поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра.
Ответ. 1/3.
Слайд 7Усеченный додекаэдр
Какую часть ребер нужно отсекать плоскостями от вершин икосаэдра, чтобы
полученный многогранник был полуправильным, называемым усеченный додекаэдр?
Слайд 8Кубооктаэдр
Для того чтобы получить еще один полуправильный многогранник, проведем в кубе
отсекающие плоскости через середины ребер, выходящих из одной вершины. В результате получим полуправильный многогранник, который называется кубооктаэдр. Его поверхность состоит из граней куба и октаэдра.
Слайд 9Икосододекаэдр
Аналогично, если в икосаэдре отсекающие плоскости провести через середины ребер, выходящих
из одной вершины, то получим многогранник, который называется икосододекаэдр. Его поверхность состоит из граней икосаэдра и додекаэдра.
Слайд 10Упражнение 1
Какой многогранник получится, если в тетраэдре отсекающие плоскости провести через
середины ребер, выходящих из одной вершины?
Ответ. Октаэдр.
Слайд 11Упражнение 2
Какой многогранник получится, если в октаэдре отсекающие плоскости провести через
середины ребер, выходящих из одной вершины?
Ответ. Кубооктаэдр.
Слайд 12Упражнение 3
Какой многогранник получится, если в додекаэдре отсекающие плоскости провести через
середины ребер, выходящих из одной вершины?
Ответ. Икосододекаэдр.
Слайд 13Усеченный кубооктаэдр
Полуправильный многогранник, изображенный на рисунке называют усеченный кубооктаэдр, хотя он
и не получается усечением кубооктаэдра. Его поверхность состоит из правильных восьмиугольников, шестиугольников и квадратов.
Слайд 14Усеченный икосододекаэдр
Полуправильный многогранник, изображенный на рисунке называют усеченный икосододекаэдр, хотя он
и не получаются усечением икосододекаэдра. Его поверхность состоит из правильных десятиугольников, шестиугольников и квадратов.
Слайд 15Ромбокубооктаэдр
На рисунке изображен многогранник, называемый ромбокубооктаэдр. Его поверхность состоит из граней
куба и октаэдра, к которым добавлены еще 12 квадратов.
Слайд 16Ромбоикосододекаэдр
На рисунке изображен многогранник, называемый ромбоикосододекаэдр. Его поверхность состоит из граней
икосаэдра, додекаэдра и еще 30 квадратов.
Слайд 17Курносый куб
На рисунке изображен многогранник, называемый курносый (иногда называют плосконосый) куб.
Его поверхность состоит из граней куба, окруженных правильными треугольниками.
Слайд 18Курносый додекаэдр
Последний многогранник Архимеда называется курносый (плосконосый) додекаэдр. Его поверхность состоит
из граней додекаэдра, окруженных правильными треугольниками.
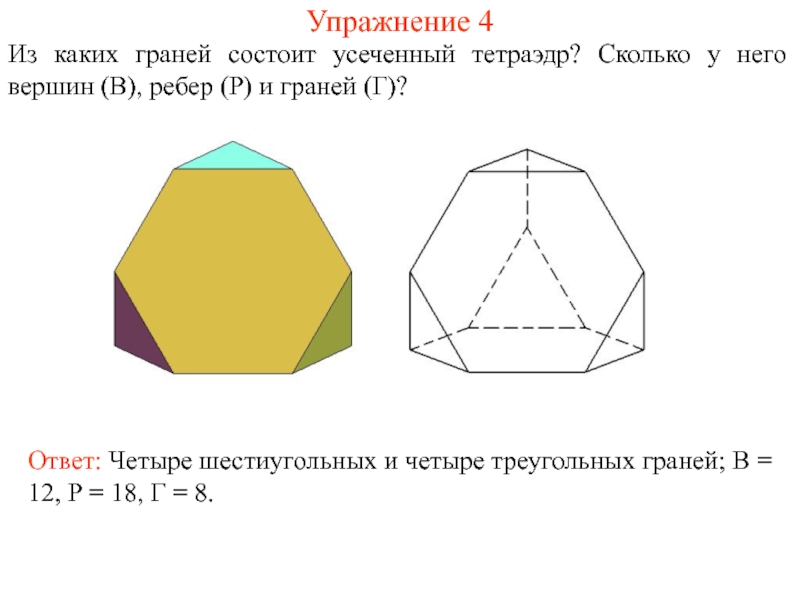
Слайд 19Упражнение 4
Из каких граней состоит усеченный тетраэдр? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Четыре шестиугольных и четыре треугольных граней; В = 12, Р = 18, Г = 8.
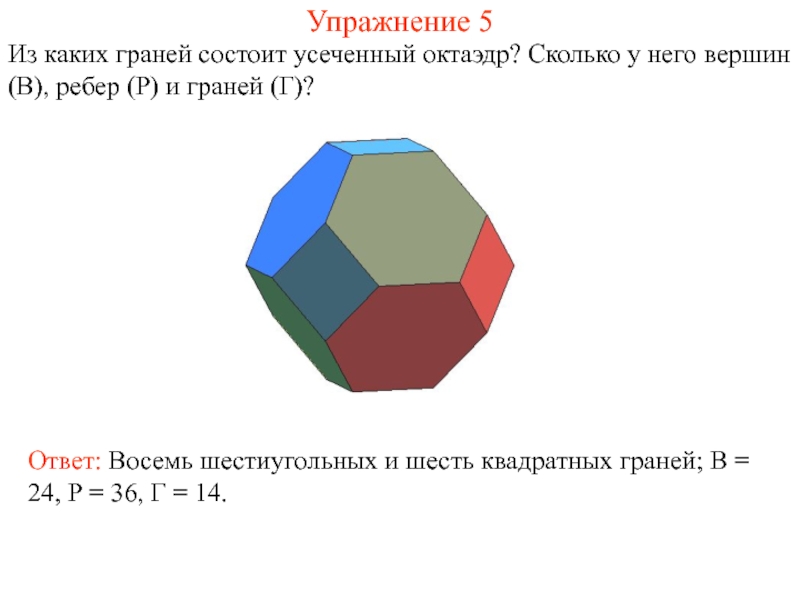
Слайд 20Упражнение 5
Из каких граней состоит усеченный октаэдр? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Восемь шестиугольных и шесть квадратных граней; В = 24, Р = 36, Г = 14.
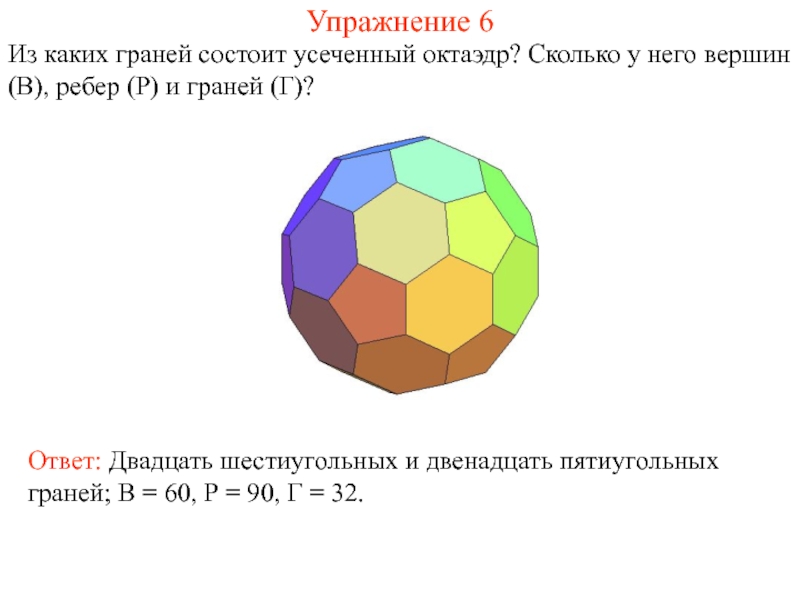
Слайд 21Упражнение 6
Из каких граней состоит усеченный октаэдр? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Двадцать шестиугольных и двенадцать пятиугольных граней; В = 60, Р = 90, Г = 32.
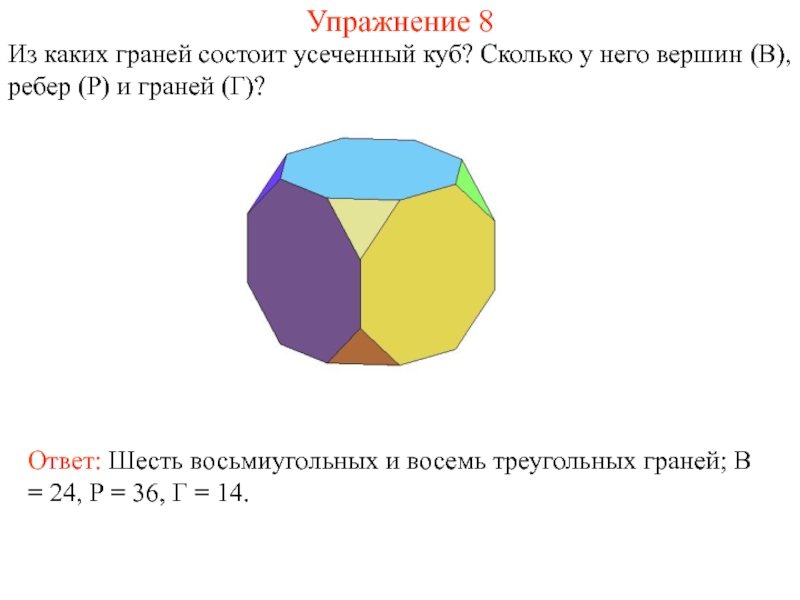
Слайд 23Упражнение 8
Из каких граней состоит усеченный куб? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Шесть восьмиугольных и восемь треугольных граней; В = 24, Р = 36, Г = 14.
Слайд 24Упражнение 9
Ребро додекаэдра равно 1. Найдите ребро полученного из него усеченного
додекаэдра.
Слайд 25Упражнение 10
Из каких граней состоит усеченный додекаэдр? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Двенадцать десятиугольных и двадцать треугольных граней; В = 60, Р = 90, Г = 32.
Слайд 27Упражнение 12
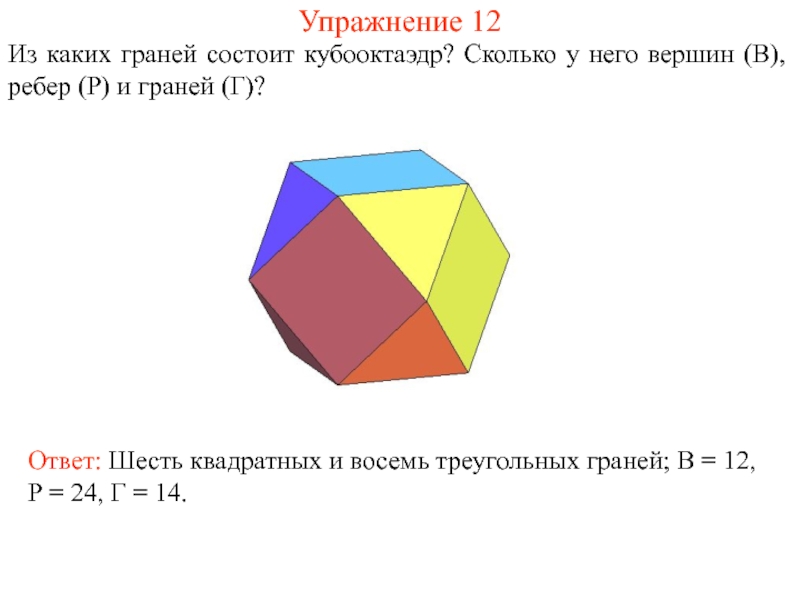
Из каких граней состоит кубооктаэдр? Сколько у него вершин (В),
ребер (Р) и граней (Г)?
Ответ: Шесть квадратных и восемь треугольных граней; В = 12, Р = 24, Г = 14.
Слайд 29Упражнение 14
Из каких граней состоит икосододекаэдр? Сколько у него вершин (В),
ребер (Р) и граней (Г)?
Ответ: Двенадцать пятиугольных и двадцать треугольных граней; В = 30, Р = 60, Г = 32.
Слайд 30Упражнение 15
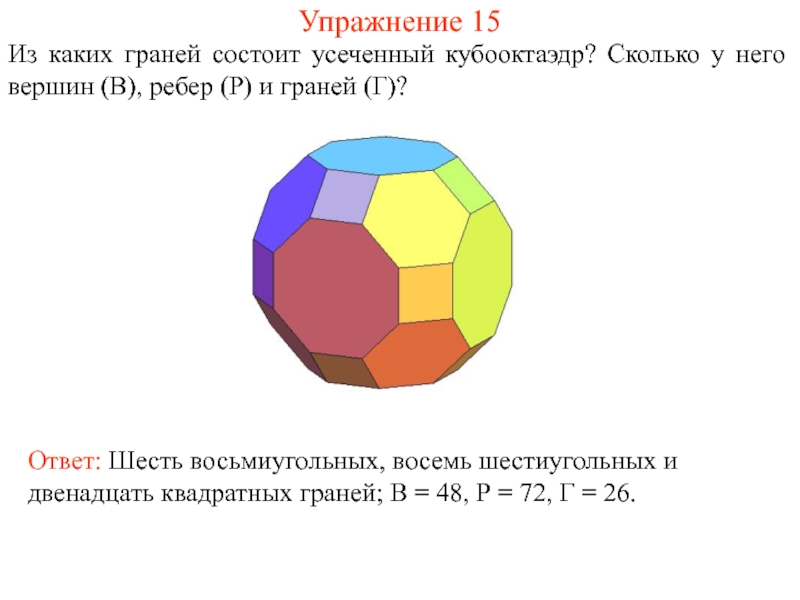
Из каких граней состоит усеченный кубооктаэдр? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Шесть восьмиугольных, восемь шестиугольных и двенадцать квадратных граней; В = 48, Р = 72, Г = 26.
Слайд 31Упражнение 16
Из каких граней состоит усеченный икосододекаэдр? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Двенадцать десятиугольных, двадцать шестиугольных и тридцать квадратных граней; В = 120, Р = 180, Г = 62.
Слайд 32Упражнение 17
Из каких граней состоит ромбокубооктаэдр? Сколько у него вершин (В),
ребер (Р) и граней (Г)?
Ответ: Восемнадцать квадратных и восемь треугольных граней; В = 24, Р = 48, Г = 26.
Слайд 33Упражнение 18
Из каких граней состоит ромбоикосододекаэдр? Сколько у него вершин (В),
ребер (Р) и граней (Г)?
Ответ: Двенадцать пятиугольных, тридцать квадратных и двадцать треугольных граней; В = 60, Р = 120, Г = 62.
Слайд 34Упражнение 19
Из каких граней состоит курносый куб? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Шесть квадратных и тридцать две треугольных граней; В = 24, Р = 60, Г = 38.
Слайд 35Упражнение 20
Из каких граней состоит курносый додекаэдр? Сколько у него вершин
(В), ребер (Р) и граней (Г)?
Ответ: Двенадцать пятиугольных и восемьдесят треугольных граней; В = 60, Р = 150, Г = 92.
Слайд 36Упражнение 21
На рисунке б) изображён многогранник, который называется псевдоархимедовым. Как он
получен из ромбокубооктаэдра (рис. а)? Является ли он полуправильным многогранником?
Ответ: Этот многогранник получается из ромбокубооктаэдра поворотом нижней восьмиугольной чаши на 45о. Он не является полуправильным многогранником.
Слайд 37Упражнение 22
Развертка какого полуправильного многогранника изображена на рисунке?
Ответ: Усеченного тетраэдра.
Слайд 38Упражнение 23
Развертка какого полуправильного многогранника изображена на рисунке?
Ответ: Усеченного октаэдра.
Слайд 39Упражнение 24
Развертка какого полуправильного многогранника изображена на рисунке?
Ответ: Усеченного куба.
Слайд 40Упражнение 25
Развертка какого полуправильного многогранника изображена на рисунке?
Ответ: Кубооктаэдра.
Слайд 41Упражнение 26
Развертка какого полуправильного многогранника изображена на рисунке?
Ответ: Пятиугольной антипризмы.
Слайд 42Упражнение 27
Развертка какого полуправильного многогранника изображена на рисунке?
Ответ: Усеченный икосаэдр.
Слайд 43Упражнение 28
Развертка какого полуправильного многогранника изображена на рисунке?
Ответ: Усеченный додекаэдр.
Слайд 44Упражнение 29
Развертка какого полуправильного многогранника изображена на рисунке?
Ответ: Икосододекаэдр.
Слайд 45Упражнение 30
Объединением каких многогранников является многогранник, представленный на рисунке? Какой многогранник
является их пересечением?
Ответ: Куб и октаэдр. Их пересечением является кубооктаэдр.
Слайд 46Упражнение 31
Разрежьте четыре равных куба на две части каждый и сложите
из них усеченный октаэдр.
Слайд 47Усеченный куб’
Выпуклый многогранник называются равногранно полуправильным, если его гранями являются равные
многоугольники и все многогранные углы – правильные. Эти многогранники двойственны полуправильным многогранникам.
На рисунке показан многогранник, двойственный усеченному кубу. Его гранями являются равные треугольники. Сколько их?
Ответ: 24.
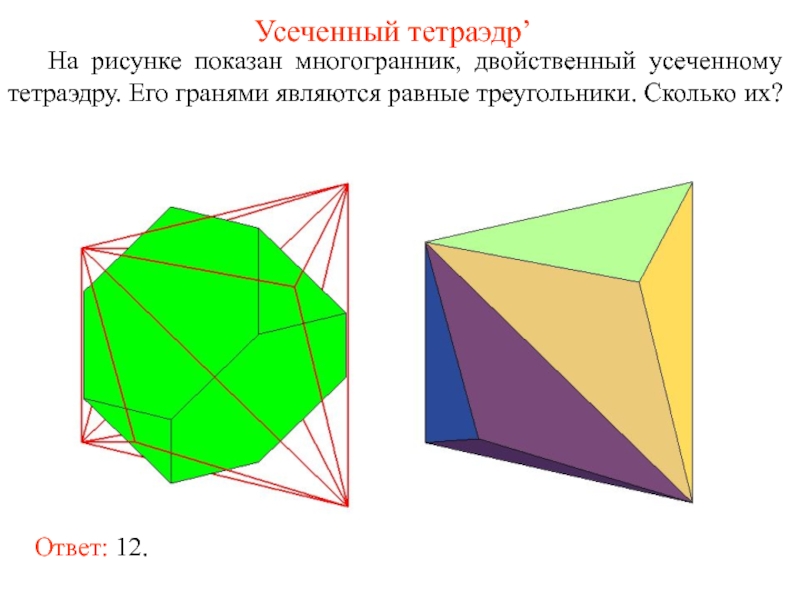
Слайд 48Усеченный тетраэдр’
На рисунке показан многогранник, двойственный усеченному тетраэдру. Его гранями являются
равные треугольники. Сколько их?
Ответ: 12.
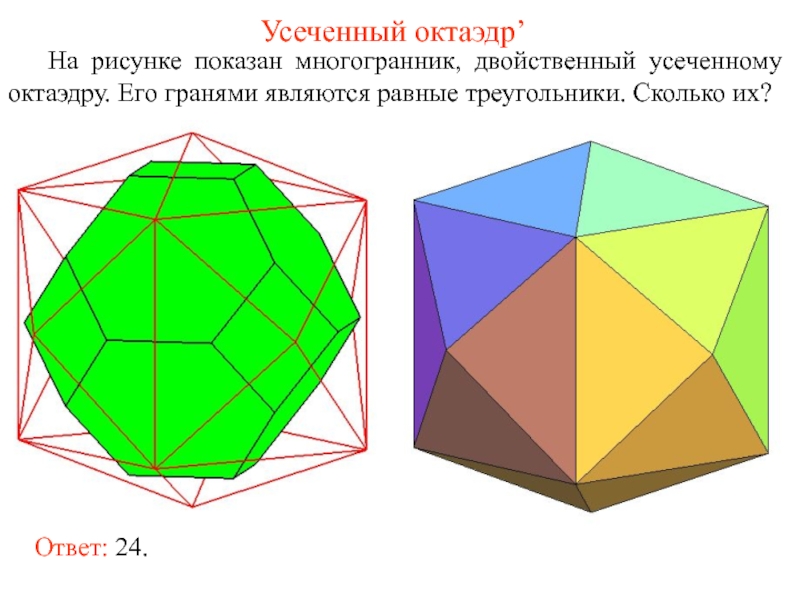
Слайд 49Усеченный октаэдр’
На рисунке показан многогранник, двойственный усеченному октаэдру. Его гранями являются
равные треугольники. Сколько их?
Ответ: 24.
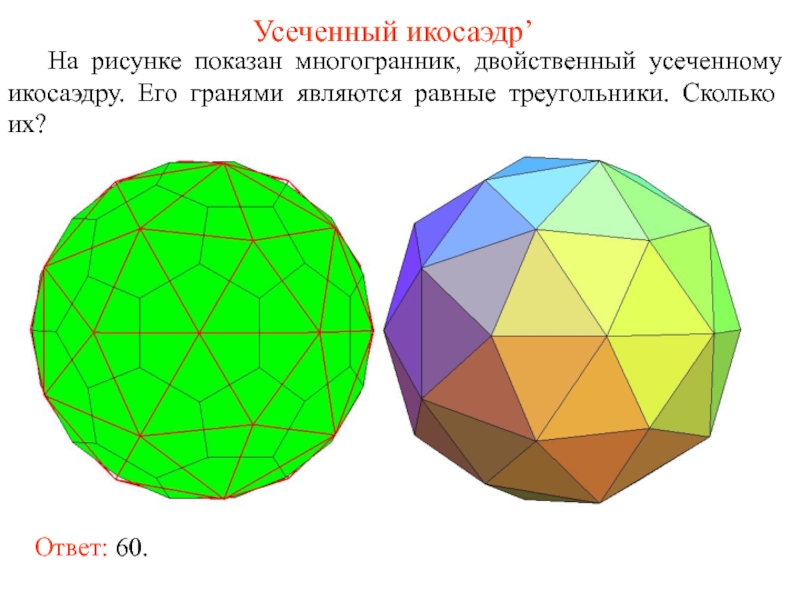
Слайд 50Усеченный икосаэдр’
На рисунке показан многогранник, двойственный усеченному икосаэдру. Его гранями являются
равные треугольники. Сколько их?
Ответ: 60.
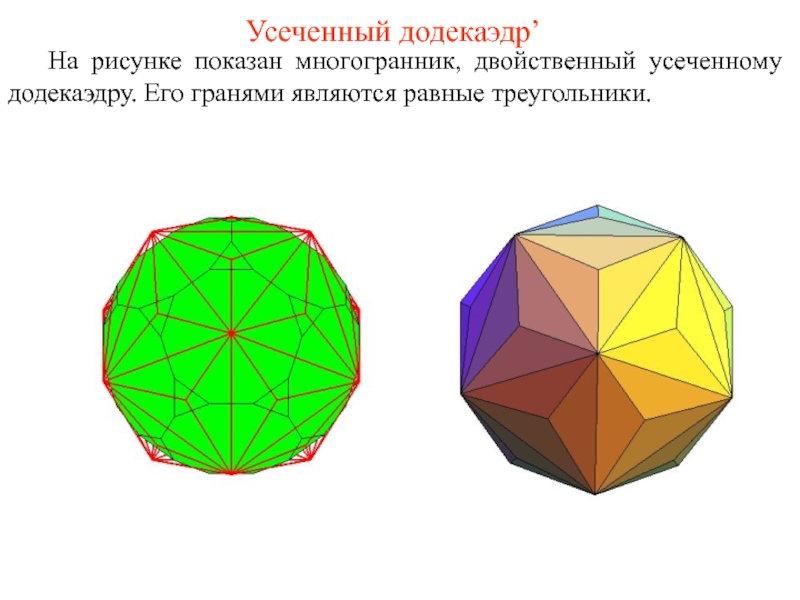
Слайд 51Усеченный додекаэдр’
На рисунке показан многогранник, двойственный усеченному додекаэдру. Его гранями являются
равные треугольники.
Слайд 52Кубооктаэдр’
На рисунке показан многогранник, двойственный кубооктаэдру. Его гранями являются равные ромбы.
Сколько их?
Ответ: 12.
Слайд 53Икосододекаэдр’
На рисунке показан многогранник, двойственный икосододекаэдру. Его гранями являются равные ромбы.
Сколько их?
Ответ: 30.
Слайд 54Усеченный кубооктаэдр’
На рисунке показан многогранник, двойственный усеченному кубооктаэдру. Его гранями являются
равные ромбы. Сколько их?
Ответ: 48.
Слайд 55Усеченный икосододекаэдр’
На рисунке показан многогранник, двойственный усеченному икосододекаэдру. Его гранями являются
равные ромбы. Сколько их?
Ответ: 120.
Слайд 56Ромбокубооктаэдр’
На рисунке показан многогранник, двойственный ромбокубо-октаэдру. Его гранями являются равные четырехугольники.
Сколько их?
Ответ: 24.
Слайд 57Курносый куб’
На рисунке показан многогранник, двойственный курносому кубу. Его гранями являются
равные пятиугольники. Сколько их?
Ответ: 24.
Слайд 58Курносый додекаэдр’
На рисунке показан многогранник, двойственный курносому додекаэдру. Его гранями являются
равные пятиугольники. Сколько их?
Ответ: 60.
