- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Политехническая олимпиада по математике презентация
Содержание
- 1. Политехническая олимпиада по математике
- 2. 9 класс, задача № 1
- 3. 9 класс, задача № 1
- 4. 9 класс, задача № 1 Из
- 5. 9 класс, задача № 2
- 6. 9 класс, задача № 2
- 7. 9 класс, задача № 3 Решение
- 8. 9 класс, задача № 4 Параллелограмм
- 9. 9 класс, задача № 4 параллелограммов Ответ
- 10. 9 класс, задача № 5; 10
- 11. 9 класс, задача № 5 Тогда
- 12. 9 класс, задача № 5 Тогда
- 13. 9 класс, задача № 6 Решите
- 14. 9 класс, задача № 6
- 15. 10 класс, задача № 1
- 16. 10 класс, задача № 1
- 17. 10 класс, задача № 1 Нет.
- 18. 10 класс, задача № 1
- 19. 10 класс, задача № 3; 11
- 20. 10 класс, задача № 3 31 Ответ
- 21. 10 класс, задача № 4 Определите
- 22. 10 класс, задача № 4 Всего
- 23. 10 класс, задача № 4
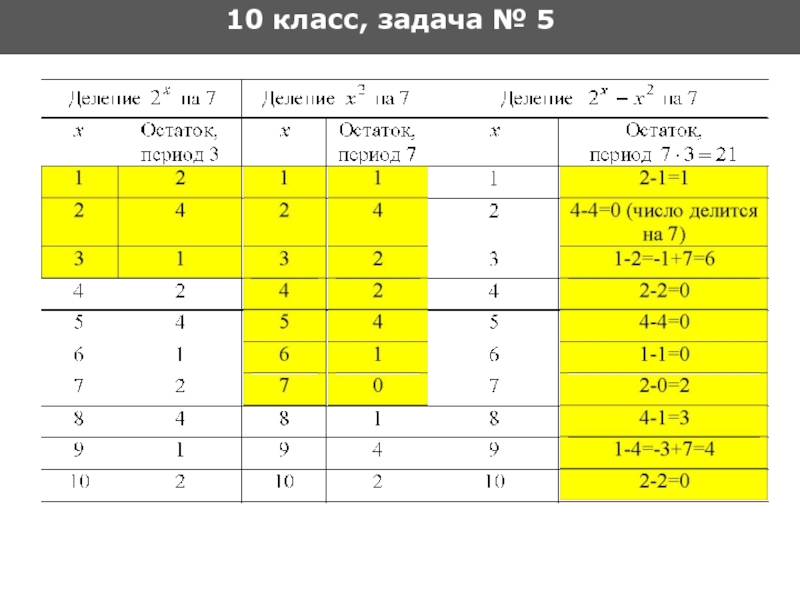
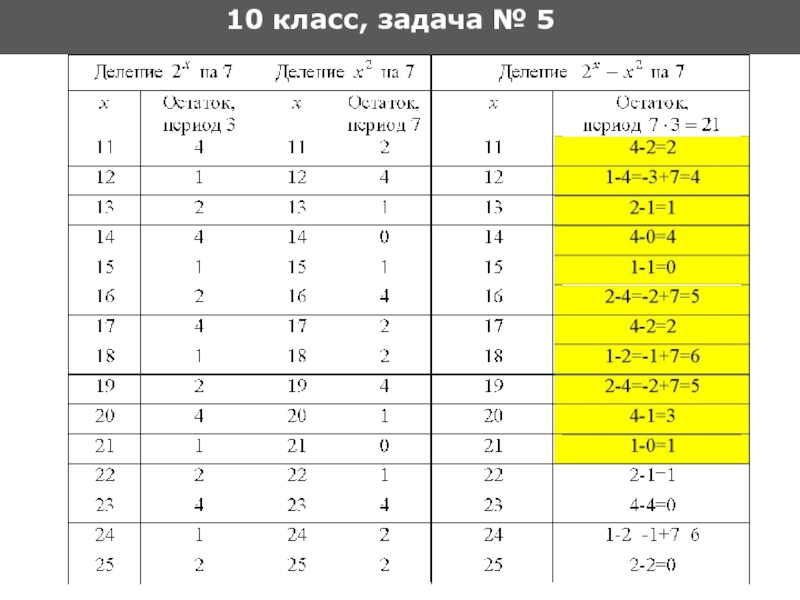
- 24. 10 класс, задача № 5 Решение
- 25. 10 класс, задача № 5
- 26. 10 класс, задача № 5
- 27. 10 класс, задача № 5 2857 Ответ
- 28. 10 класс, задача № 6 Найдите
- 29. 10 класс, задача № 7 Известно,
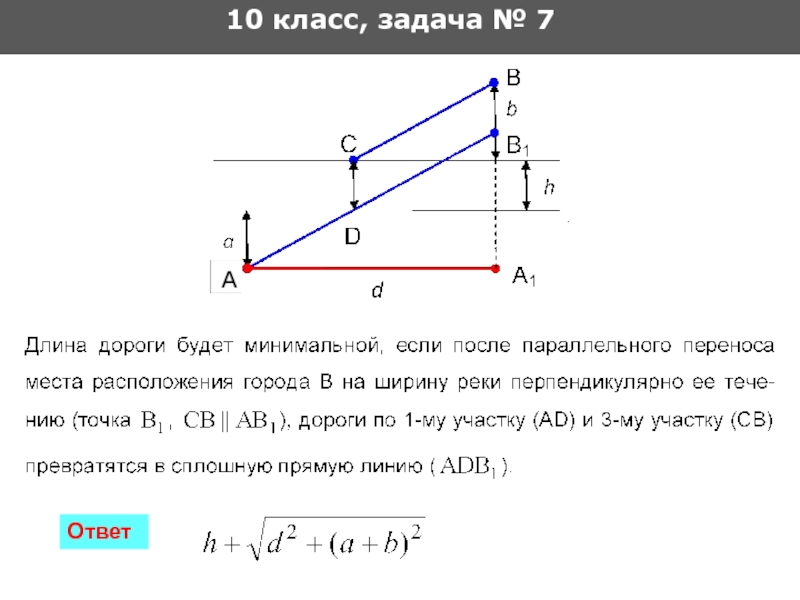
- 30. 10 класс, задача № 7 Длина
- 31. 10 класс, задача № 7 Ответ
- 32. 11 класс, задача № 1 Решение
- 33. 11 класс, задача № 1
- 34. 11 класс, задача № 2
- 35. 11 класс, задача № 2
- 36. 11 класс, задача № 2 Нет.
- 37. 11 класс, задача № 2
- 38. 11 класс, задача № 2
- 39. 11 класс,
- 40. 11 класс,
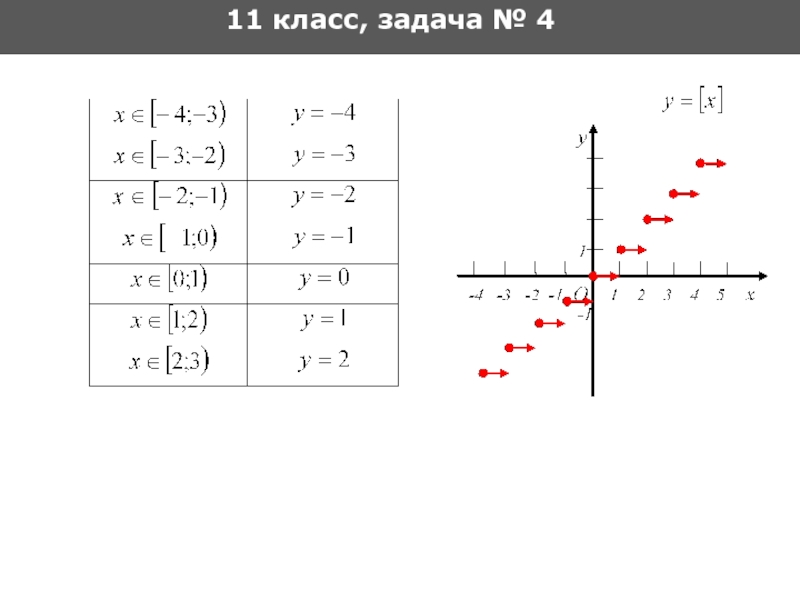
- 41. 11 класс, задача № 4 Решение
- 42. 11 класс, задача № 4
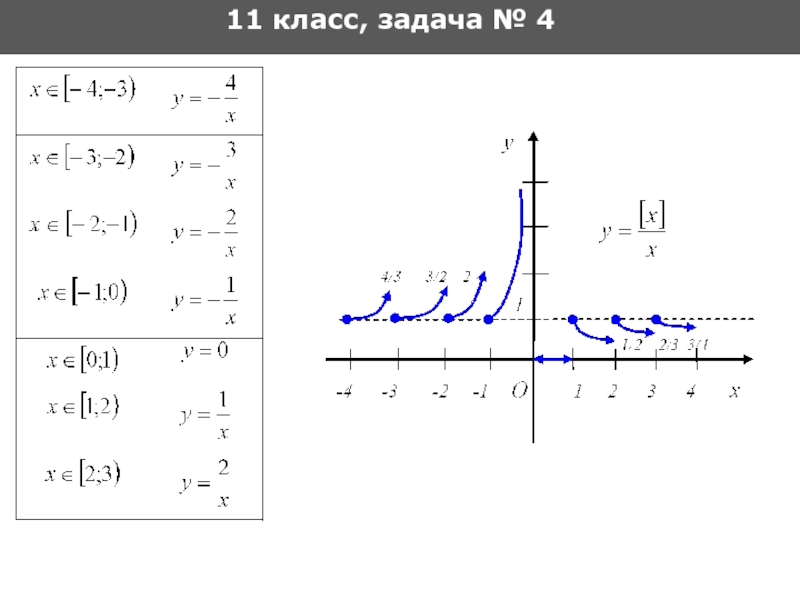
- 43. 11 класс, задача № 4
- 44. 11 класс, задача № 4
- 45. 11 класс,
- 46. 11
- 47. 11 класс, задача № 7 Решение
- 48. 11 класс,
- 49. Спасибо за внимание!
Слайд 1ПОЛИТЕХНИЧЕСКАЯ ОЛИМПИАДА - 2017
Омский государственный
технический университет
МАТЕМАТИКА
Омск, 16.04.2017
Слайд 2
9 класс, задача № 1
Докажите, что круги, построенные на сторонах выпуклого
Возьмем произвольную точку Р внутри выпуклого четырехугольника ABCD и соединим ее с вершинами четырехугольника.
Тогда
Решение
Слайд 3
9 класс, задача № 1
Для любого треугольника это утверждение также справедливо.
Слайд 4
9 класс, задача № 1
Из правильности следует
Таким образом, точка Р не
Действительно, рассмотрим правильный пятиугольник и возьмем точку Р центр пятиугольника, соединив точку Р с вершинами.
Для пятиугольников это утверждение несправедливо.
Слайд 6
9 класс, задача № 2
Способ 2.
Применим алгоритм Евклида
Таким образом, остаток
Решение
Слайд 8
9 класс, задача № 4
Параллелограмм определяется двумя парами параллельных прямых, соответственно,
Решение
Слайд 11
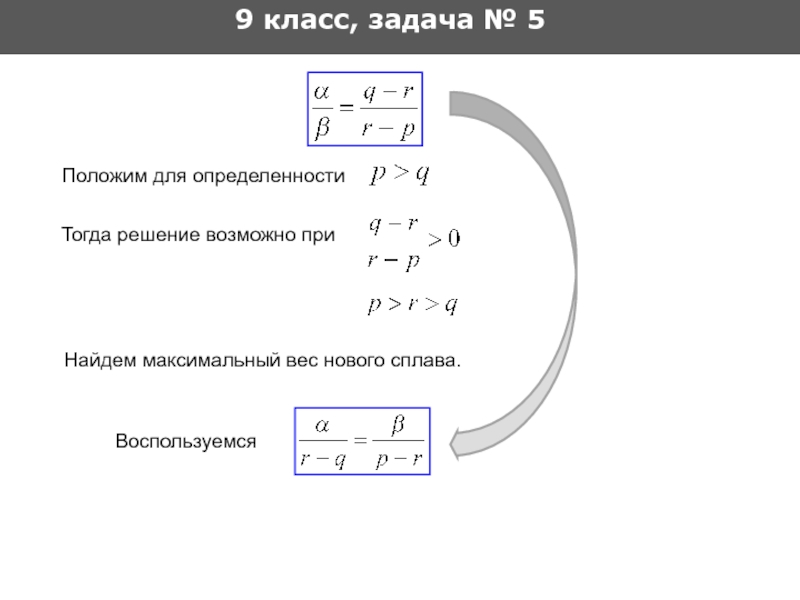
9 класс, задача № 5
Тогда решение возможно при
Положим для определенности
Найдем максимальный вес нового сплава.
Воспользуемся
Слайд 13
9 класс, задача № 6
Решите систему уравнений
Возводим второе уравнение в квадрат
Вычтем полученное уравнение из первого уравнения системы и получим
Решение
Слайд 14
9 класс, задача № 6
Проверка показывает, что все четыре пары чисел
Ответ
Слайд 15
10 класс, задача № 1
Тогда
Решение
Слайд 16
10 класс, задача № 1
Для любого треугольника это утверждение также справедливо.
Слайд 17
10 класс, задача № 1
Нет.
Докажем, что существует пятиугольник, для которого
Действительно, рассмотрим правильный пятиугольник и возьмем точку Р центр пятиугольника, соединив точку Р с вершинами.
Из правильности следует
Слайд 18
10 класс, задача № 1
Таким образом, точка Р не принадлежит ни
Слайд 21
10 класс, задача № 4
Определите количество решений системы уравнений
Воспользуемся методом
Решение
Слайд 22
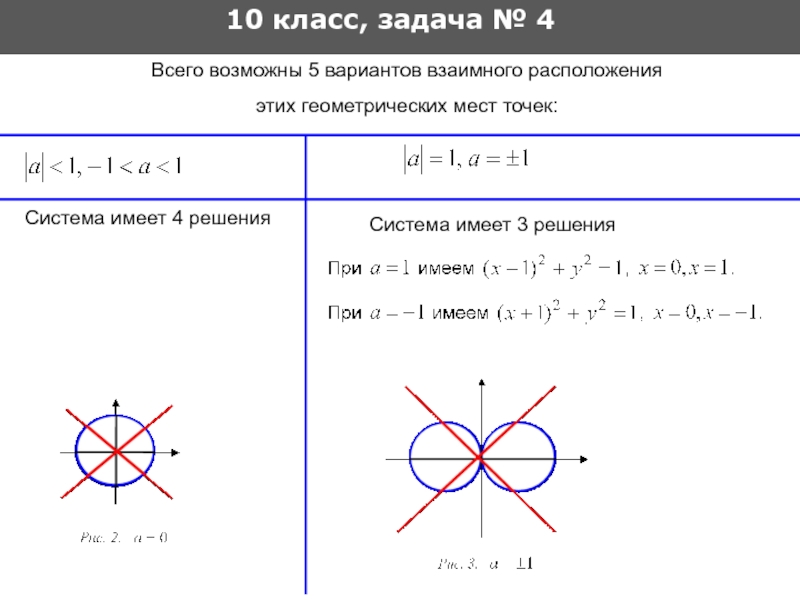
10 класс, задача № 4
Всего возможны 5 вариантов взаимного расположения
этих
Система имеет 3 решения
Система имеет 4 решения
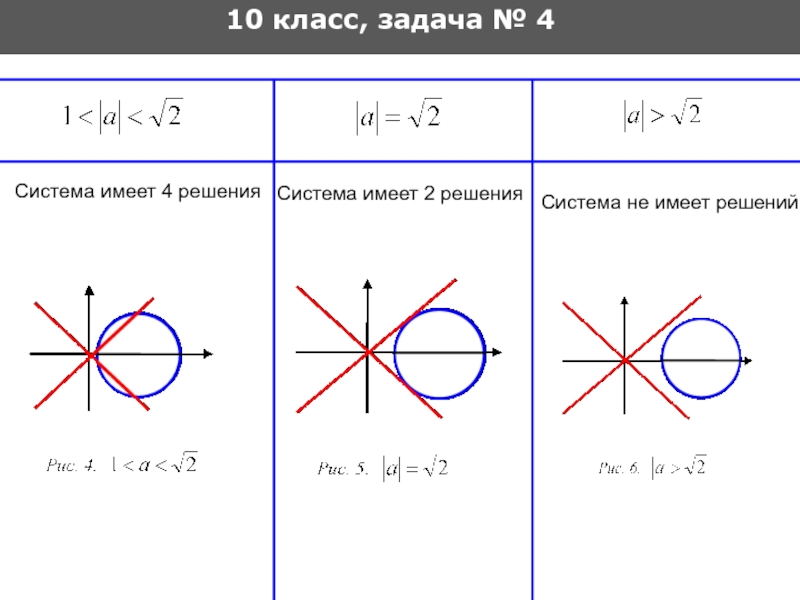
Слайд 23
10 класс, задача № 4
Система имеет 4 решения
Система имеет 2
Система не имеет решений
Слайд 29
10 класс, задача № 7
Известно, что на плоскости кратчайшее расстояние между
Решение
Слайд 30
10 класс, задача № 7
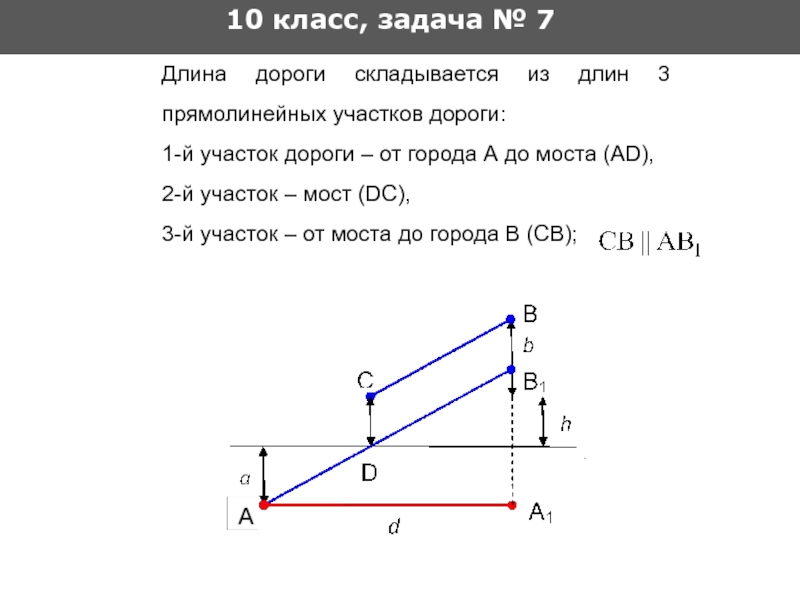
Длина дороги складывается из длин 3 прямолинейных
1-й участок дороги – от города А до моста (AD),
2-й участок – мост (DC),
3-й участок – от моста до города В (CB);
Слайд 32
11 класс, задача № 1
Решение
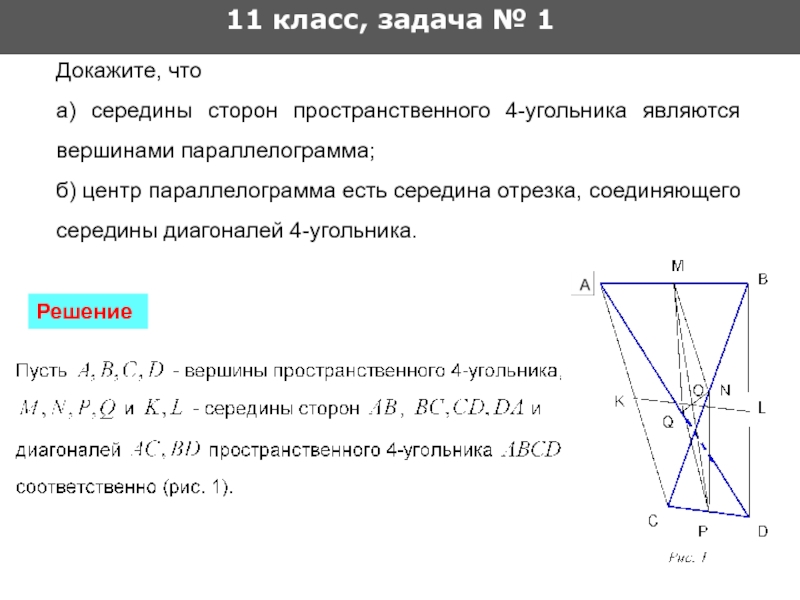
Докажите, что
а) середины сторон пространственного 4-угольника
б) центр параллелограмма есть середина отрезка, соединяющего середины диагоналей 4-угольника.
Слайд 34
11 класс, задача № 2
Тогда
Решение
Слайд 35
11 класс, задача № 2
Для любого треугольника это утверждение также справедливо.
Слайд 36
11 класс, задача № 2
Нет.
Докажем, что существует пятиугольник, для которого
Действительно, рассмотрим правильный пятиугольник и возьмем точку Р центр пятиугольника, соединив точку Р с вершинами.
Из правильности следует
Слайд 37
11 класс, задача № 2
Таким образом, точка Р не принадлежит ни
Слайд 48
11 класс, задача № 7
Для этого рассмотрим сумму всех элементов последовательности
(так как суммы в скобках одинаковы)