- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Полезные функции Matlab’a презентация
Содержание
- 1. Полезные функции Matlab’a
- 2. Функции работы с изображениями Imshow Imwrite imread
- 3. Функции конвертации Im2bw Im2double Rgb2gray Uint8 uint16
- 4. Функции работы с матрицами Max Min Sum
- 5. Векторизация meshgrid
- 6. Общие задания
- 7. Вывод сферического волновоо фронта Задача: вывести на
- 8. Перестановки Задача: реализовать функцию, принимающую на вход
- 9. Дискретное преобразование Фурье Дискретное
- 10. Дискретное преобразование Фурье Обратное дискретное преобразование Фурье Поворачивающий множитель
- 11. Свойства поворачивающего множителя k – степень, а
- 12. Свойства поворачивающего множителя Некоторое комплексное число в
- 13. Свойства поворачивающего множителя wkN , модуль равен
- 14. Теорема 0 Теорема: Если комплексное число представлено
- 15. Теорема 1 Теорема: Величина периодична по k и по n с
- 16. Теорема 1 Доказательство:
- 17. Теорема 2 Теорема: Для величины справедлива формула: Доказательство:
- 18. Быстрое преобразование Фурье Идея: Необходимо разделить сумму
- 19. Быстрое преобразование Фурье Применяют: «Прореживание по времени»,
- 20. Теорема 3 Определим еще две последовательности: {x[even]} и {x[odd]} через последовательность {x} следующим
- 21. ДПФ для чётных/нечётных k = 0…N/2-1 k = N/2…N-1
Слайд 7Вывод сферического волновоо фронта
Задача: вывести на экран картинку сферического (кругового в
2D случае) волнового фронта
Слайд 8Перестановки
Задача: реализовать функцию, принимающую на вход произвольный набор элементов, результатом работы
которой является список всех возможных перестановок этих элементов.
input: a b c output: a b c; a c b;
b a c; b c a; c a b; c b a.
input: a b c output: a b c; a c b;
b a c; b c a; c a b; c b a.
Слайд 9Дискретное преобразование Фурье
Дискретное преобразование Фурье
N – число элементов последовательности
(размер массива)
k – k-ый элемент нового массива
j – мнимая единица (в матлабе переменная i)
k – k-ый элемент нового массива
j – мнимая единица (в матлабе переменная i)
Слайд 10Дискретное преобразование Фурье
Обратное дискретное преобразование Фурье
Поворачивающий множитель
Слайд 11Свойства поворачивающего множителя
k – степень, а не индекс. Если равен 1,
то не записываем
ДПФ через поворачивающий множитель
ДПФ через поворачивающий множитель
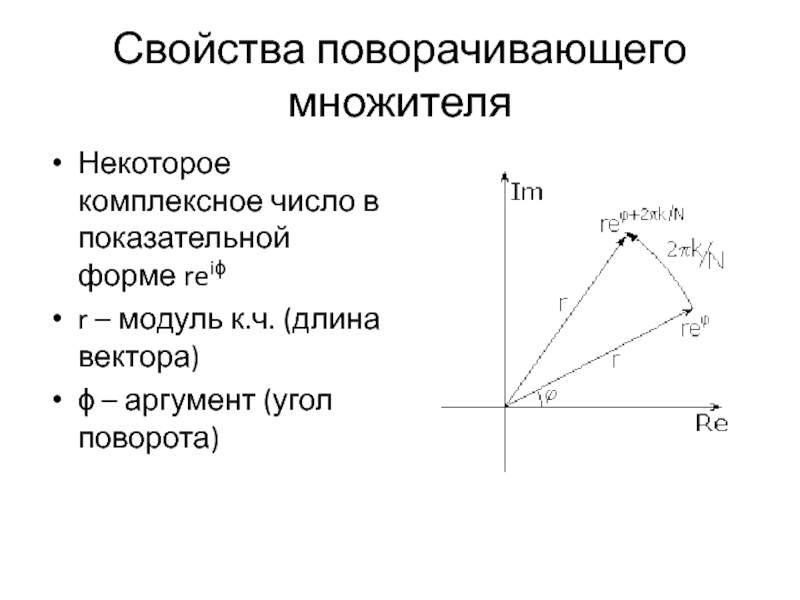
Слайд 12Свойства поворачивающего множителя
Некоторое комплексное число в показательной форме reiϕ
r – модуль
к.ч. (длина вектора)
ϕ – аргумент (угол поворота)
ϕ – аргумент (угол поворота)
Слайд 13Свойства поворачивающего множителя
wkN , модуль равен 1, а фаза – 2π/N
При умножении к.ч. В показательной форме модули перемножаются, а аргументы складываются.
Тогда, перемножение исходного числа на поворачивающий множитель изменит только угол поворота
Т.о. геометрический смысл преобразования Фурье состоит в том, чтобы представить N комплексных чисел-векторов из набора {x}, каждое в виде суммы векторов из набора {X}, повернутых на углы, кратные 2π/N
Слайд 14Теорема 0
Теорема:
Если комплексное число представлено в виде e j2πN, где N - целое, то это
число e j2πN = 1.
Доказательство:
По формуле Эйлера, и ввиду периодичности синуса и косинуса: e j2πN = cos(2πN) + j sin(2πN) = cos 0 + j sin 0 = 1 + j0 = 1
Доказательство:
По формуле Эйлера, и ввиду периодичности синуса и косинуса: e j2πN = cos(2πN) + j sin(2πN) = cos 0 + j sin 0 = 1 + j0 = 1
Слайд 15Теорема 1
Теорема:
Величина периодична по k и по n с периодом N. То есть, для любых целых l и m выполняется
равенство:
Слайд 16Теорема 1
Доказательство:
Величина -h = -(nl+mk+mlN) - целая, так как все множители целые, и
все слагаемые целые. Значит, мы можем применить Теорему 0
Слайд 18Быстрое преобразование Фурье
Идея:
Необходимо разделить сумму в формуле ДПФ из N слагаемых на две
суммы по N/2 слагаемых, и вычислить их по отдельности. Для вычисления каждой из подсумм, надо их тоже разделить на две и т.д.
Необходимо повторно использовать уже вычисленные слагаемые.
Необходимо повторно использовать уже вычисленные слагаемые.
Слайд 19Быстрое преобразование Фурье
Применяют:
«Прореживание по времени», когда в первую сумму попадают слагаемые
с четными номерами, а во вторую - с нечетными
ИЛИ
«Прореживание по частоте», когда в первую сумму попадают первые N/2 слагаемых, а во вторую - остальные.
В силу специфики алгоритма приходится применять только N, являющиеся степенями 2.
ИЛИ
«Прореживание по частоте», когда в первую сумму попадают первые N/2 слагаемых, а во вторую - остальные.
В силу специфики алгоритма приходится применять только N, являющиеся степенями 2.
Слайд 20Теорема 3
Определим еще две последовательности: {x[even]} и {x[odd]} через последовательность {x} следующим образом:
x[even]n =x2n,
x[odd]n =x2n+1, (*)
n = 0, 1,..., N/2-1,
Пусть
к этим последовательностям применены ДПФ и получены результаты в виде двух новых последовательностей {X[even]} и {X[odd]} по N/2элементов в каждой.
Утверждается, что элементы последовательности {X} можно выразить через элементы последовательностей {X[even]} и {X[odd]} по формуле:
(**)
Утверждается, что элементы последовательности {X} можно выразить через элементы последовательностей {X[even]} и {X[odd]} по формуле:
(**)


















![Теорема 3Определим еще две последовательности: {x[even]} и {x[odd]} через последовательность {x} следующим образом:x[even]n =x2n, x[odd]n =x2n+1, (*) n = 0, 1,..., N/2-1,Пусть к этим](/img/tmb/3/249529/965629c4613ff99bfbd7492432ff188d-800x.jpg)






