- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Похідна. Фізичний і геометричний зміст похідної презентация
Содержание
- 1. Похідна. Фізичний і геометричний зміст похідної
- 2. Похідна та диференційованість функції Функція f
- 3. В чому полягає суть фізичного
- 4. Ми були об'єднані в групи ЕКСПЕРТИ ДОСЛІДНИКИ
- 5. Фізичний зміст похідної
- 6. І.Ньютон сформулював дві основні проблеми математичного
- 7. 1). Задача про миттєву швидкість:
- 8. 3). Друга похідна: (t)
- 9. 4). Приклад:
- 10. Висновок:
- 11. Використання похідної в фізиці. (ГРУПА ДОСЛІДНИКІВ)
- 12. під редакцією М.І.Сканаві. ”Збірник конкурсних задач“
- 13. Тіло масою m0 рухається
- 14. Доведення: F=m0a a(t)=V’(t)=S”(t); S’(t)=(αt2+ βt+ λ)’=2αt+β; a(t)=S”(t)=(2αt+ β)’=2α; a(t)=2α, α=const;
- 15. Сила, що діє на тіло – стала. Висновок
- 16. Задача 15.121 Тіло масою m0 рухається
- 17. Доведення F=m0a;
- 18. Сила, що діє на тіло, пропорційна кубу пройденого шляху. Висновок:
- 19. Геометричний зміст похідної
- 20. N дотична січна
- 21. y x
- 23. Завдання з ЗНО
- 24. 1) Обчисліть
- 25. 2) До графіка функції
- 26. 3) На малюнку зображено графік функції
- 27. 4) На малюнку зображений графік функції
- 28. 5) Знайдіть, при яких значеннях
- 29. Висновки групи експертів
- 31. y1=k1x +b1,
- 32. Задача 1
- 35. 3) y1=kx +b1, y2=k2x +b2,
- 36. Записати рівняння дотичної до
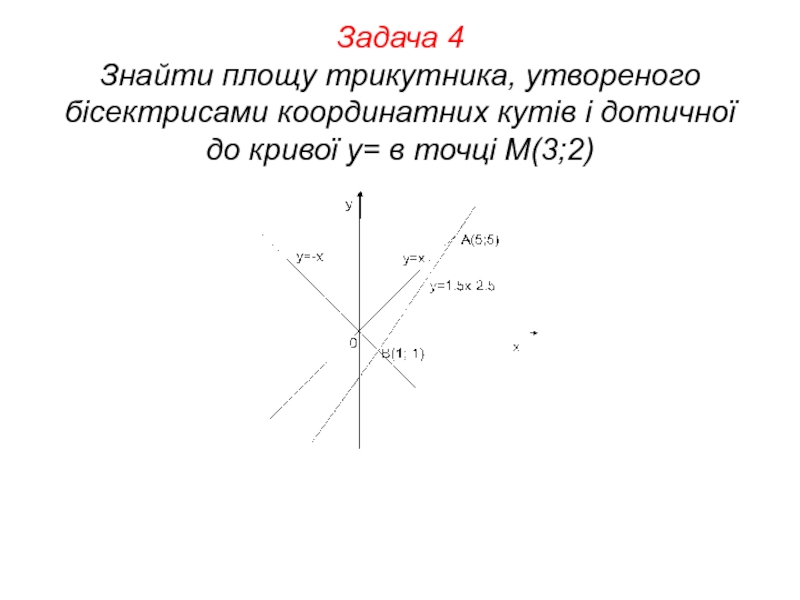
- 41. Задача 4 Знайти площу трикутника, утвореного
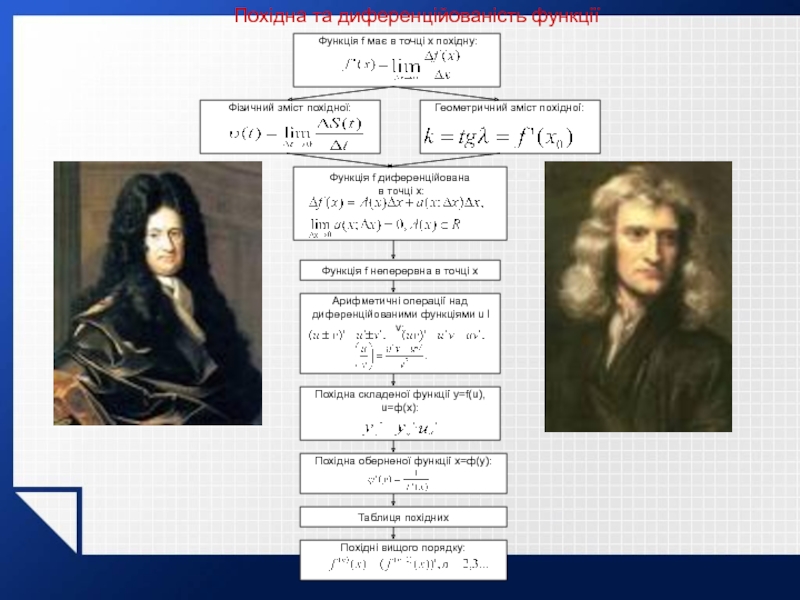
Слайд 2Похідна та диференційованість функції
Функція f має в точці x похідну:
Фізичний
Геометричний зміст похідної:
Функція f диференційована
в точці x:
Функція f неперервна в точці x
Арифметичні операції над
диференційованими функціями u I v:
Похідна складеної функції y=f(u),
u=ф(x):
Похідна оберненої функції x=ф(y):
Таблиця похідних
Похідні вищого порядку:
Слайд 3 В чому полягає суть фізичного та геометричного змісту похідної
Слайд 6
І.Ньютон сформулював дві основні проблеми математичного аналізу:
1). Довжина шляху, який долається,
2). Швидкість руху постійно дана; необхідно знайти довжину пройденого у запропонований час шляху.
Слайд 71). Задача про миттєву швидкість:
2). Задача про знаходження змінного струму, який
Слайд 13 Тіло масою m0 рухається прямолінійно за законом
α, β, λ –сталі
Довести, що сила яка діє на тіло стала
Задача 15.120.
Слайд 14Доведення:
F=m0a
a(t)=V’(t)=S”(t);
S’(t)=(αt2+ βt+ λ)’=2αt+β;
a(t)=S”(t)=(2αt+ β)’=2α;
a(t)=2α,
α=const;
Слайд 16Задача 15.121
Тіло масою m0 рухається прямолінійно за законом
Довести, що сила, яка діє на тіло, пропорційна кубу пройденого шляху.
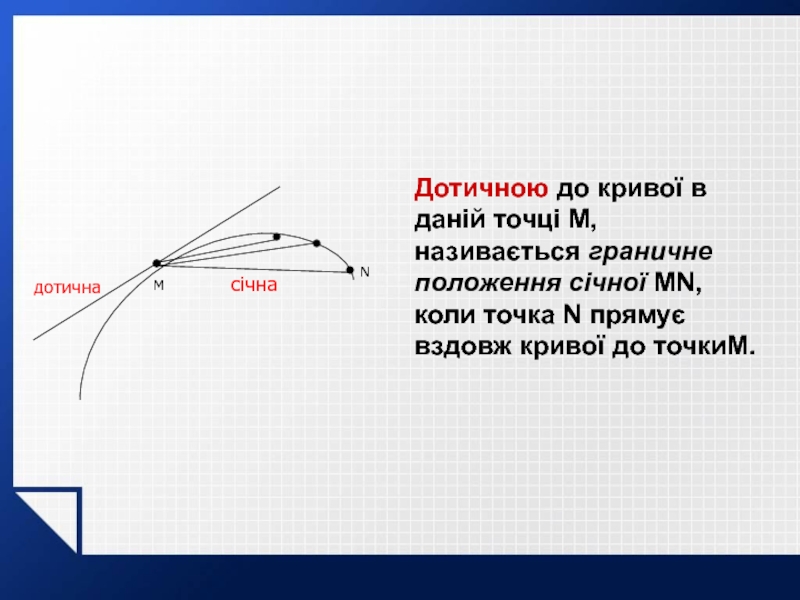
Слайд 20N
дотична
січна
M
Дотичною до кривої в даній точці M, називається граничне положення січної
Слайд 24 1) Обчисліть , якщо кут
Розв’язання
Слайд 25 2) До графіка функції
Розв’язання
Слайд 263) На малюнку зображено графік функції
y
x
1
1
Розв’язання
Знайти значення
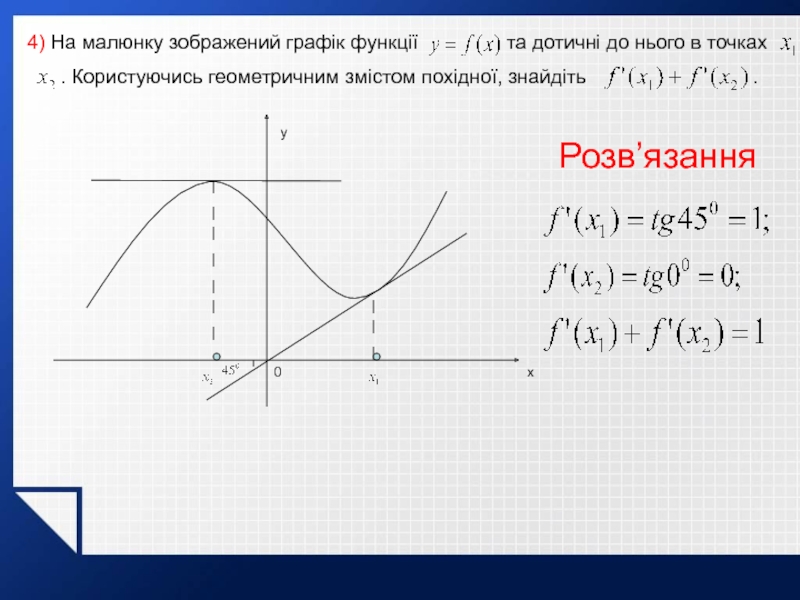
Слайд 274) На малюнку зображений графік функції
. Користуючись геометричним змістом похідної, знайдіть .
y
x
0
Розв’язання
Слайд 28 5) Знайдіть, при яких значеннях параметра а дотична до
Розв’язання
Слайд 32 Задача 1
На параболі y=
Слайд 33 Розв'язання
1) y =
Дана січна проходить через точки :
(-1;3), (3;-5)
Складаємо рівняння січної:
3 = -k + b; 8= -4k,
-5 =3k + b; k= -2, то b=1
y= -2x +1 – рівняння січної
Слайд 34
2)y=f(x0) + f
f(x0)=4 - x02;
f '(x0)= -2x0;
y =4- x02 - 2x0(x-x0),
y = -2x0x +x02 + 4,
Слайд 35
3) y1=kx +b1, y2=k2x +b2,
k1=k2
4)За умовою паралельності прямих, маємо :
-2x0= -2
x0=1.
Отже, y = -2x-3 - шукане рівняння
дотичної.
Слайд 36 Записати рівняння дотичної до графіка функції f(x)= -x2+4,
Задача 2
Слайд 37
y = f(x0) +f '(x0)(x-x0),
f (x0) = -x02+4,
f '(x0) = -2x0,
y= -x02 +4 - 2x0(x-x0),
y= -2x0x +x02 +4 - рівняння дотичної
y= 0,5x +1 - рівняння прямої перпендикулярної до дотичної
Слайд 39
За умовою перпендикулярності
якщо k1= -2x0, k2=0,5,то -2x0·0,5= -1,x0=1.
Отже, y= -2x+5 - шукане рівняння дотичної
Слайд 40
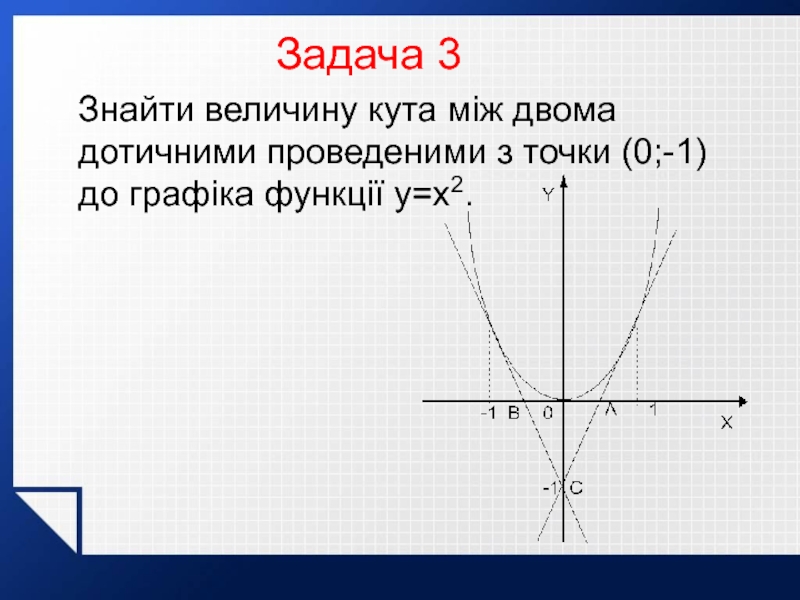
Знайти величину кута між двома дотичними проведеними з точки (0;-1) до графіка функції y=x2.