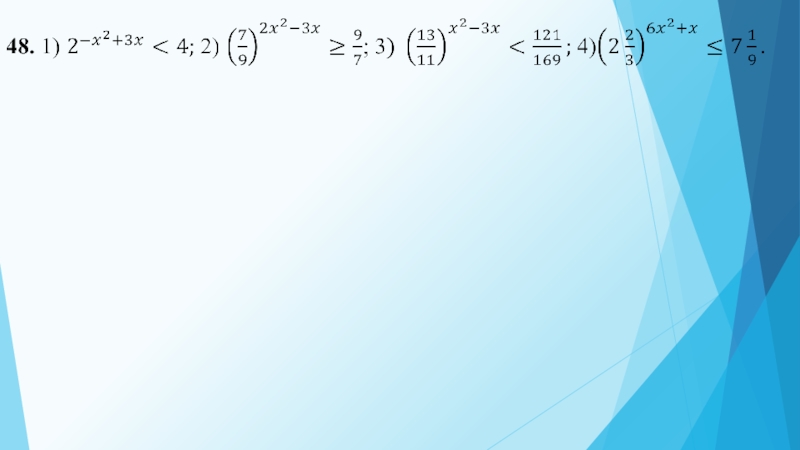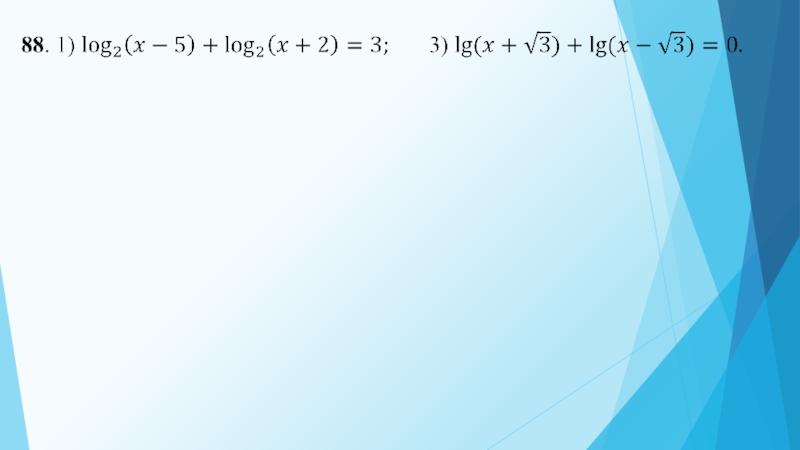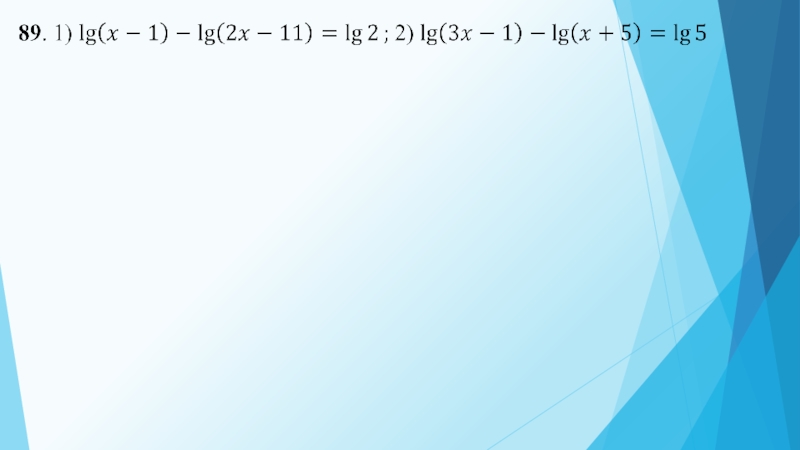- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка к экзамену. Решение уравнений и неравенств презентация
Содержание
- 1. Подготовка к экзамену. Решение уравнений и неравенств
- 2. откуда Задача 1. Решить уравнение
- 3.
- 4. Решение.
- 5. Решение. Введем новую переменную
- 6. Показательные неравенства Неравенства, в которых неизвестное содержится
- 7.
- 8. Получаем:
- 9.
- 10.
- 11.
- 12. Логарифмические уравнения. При решении логарифмических уравнений
- 13. Решение. 1. Находим ОДЗ:
- 14.
- 15.
- 16. Решение логарифмических неравенств:
- 17. Решение. 1) Находим ОДЗ:
Слайд 2откуда
Задача 1.
Решить уравнение
Решение.
Запишем уравнение в виде
откуда
Ответ.
Задача
Решить уравнение
Решение.
Так как
Получаем:
Слайд 5
Решение.
Введем новую переменную
Получаем квадратное уравнение:
Находим корни квадратного уравнения:
Возвращаемся к
Решений нет.
Ответ.
Слайд 6Показательные неравенства
Неравенства, в которых неизвестное содержится в показателе степени, называются показательными
Алгоритм решения показательных неравенств.
Слайд 12Логарифмические уравнения.
При решении логарифмических уравнений обязательно учитывается ОДЗ (область допустимых значений)
Слайд 13
Решение.
1. Находим ОДЗ:
Приводим уравнение к такому виду, чтобы обе части
Два логарифма с одинаковыми основаниями равны тогда и только тогда, когда равны их логарифмируемые выражения:
Проверяем удовлетворяет ли найденный корень ОДЗ: