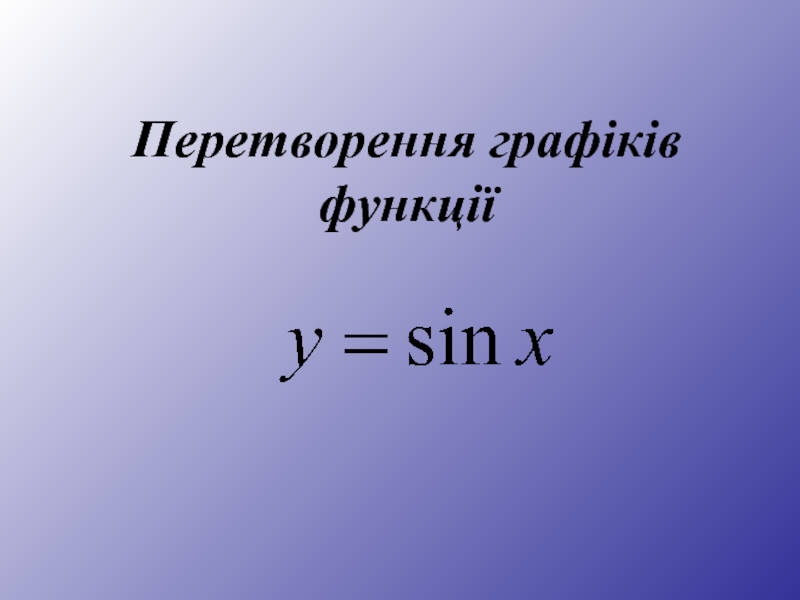- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Побудова графіків тригонометричних функцій презентация
Содержание
- 1. Побудова графіків тригонометричних функцій
- 2. Практичне застосування тригонометричних функцій Синусоїда – хвилеподібна
- 3. Зміна будь-якої величини за законом синуса називається
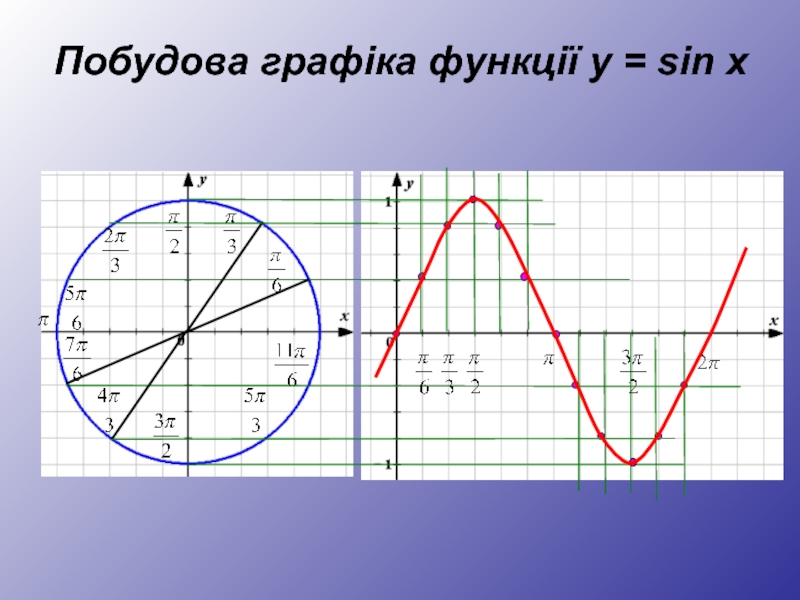
- 4. Побудова графіка функції y = sin x
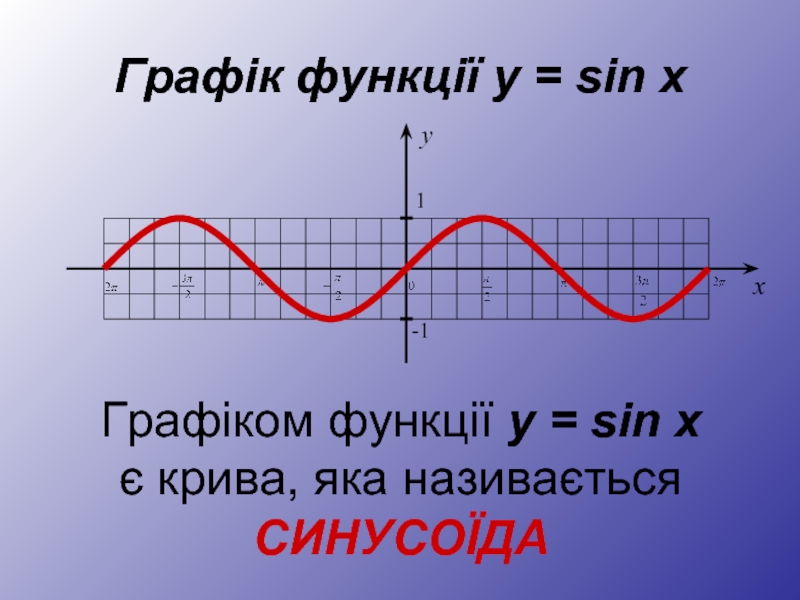
- 5. Графік функції y = sin x Графіком
- 6. Перетворення графіків функції
- 7. Перетворення графіків функції y = sin x
- 8. Перетворення графіків функції y = sin x
- 9. Перетворення графіків функції y = sin x
- 10. Перетворення графіків функції y = sin x
- 11. Перетворення графіків функції y = sin x
- 12. Перетворення графіків функції y = sin x
- 13. Перетворення графіків функції y = sin x
- 14. Перетворення графіків функції y = sin x
- 15. Перетворення графіків функції y = sin x
- 16. Перетворення графіків функції y = sin x
- 17. Перетворення графіків функції y = sin x
- 18. Перетворення графіків функції y = sin x
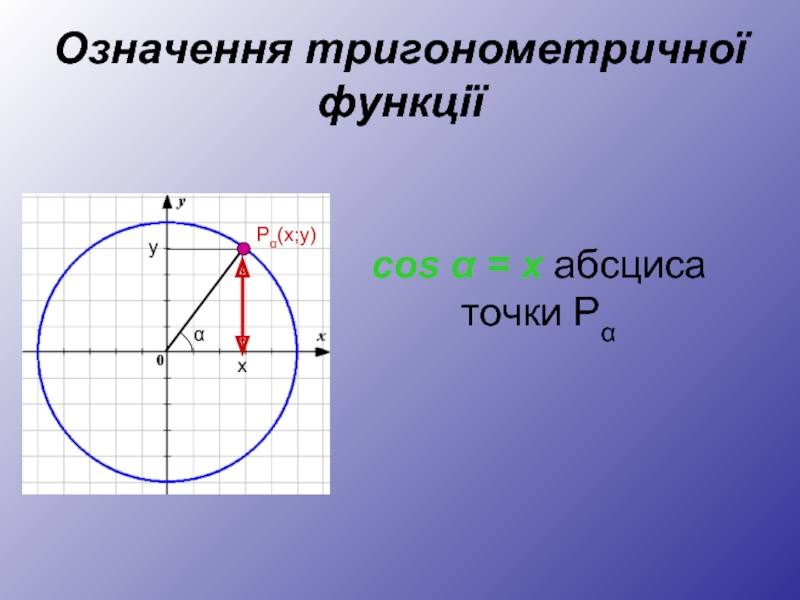
- 19. Означення тригонометричної функції cos α = x абсциса точки Pα
- 20. Побудова графіка функції y = cos x
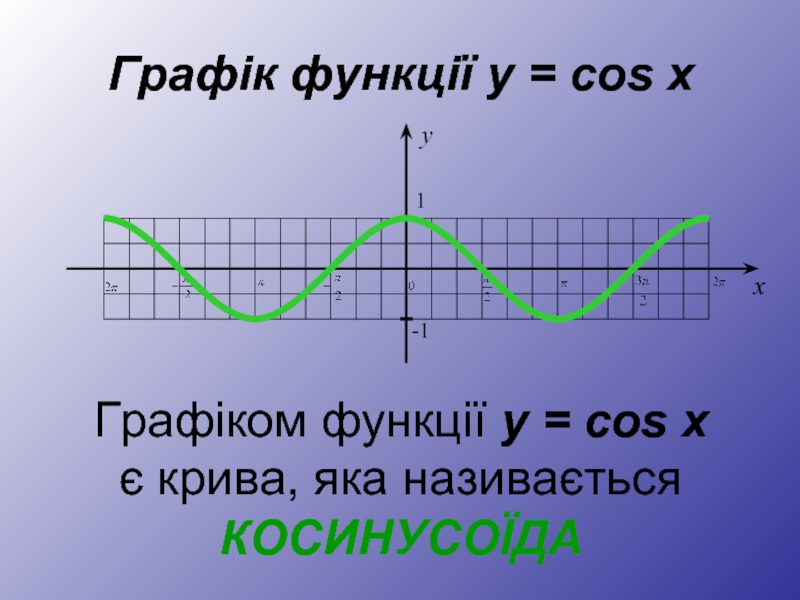
- 21. Графік функції y = cos x Графіком
- 22. Перетворення графіків функції y = cos x
- 23. y 1 -1 x Побудувати графік функції
- 24. х у 1 0
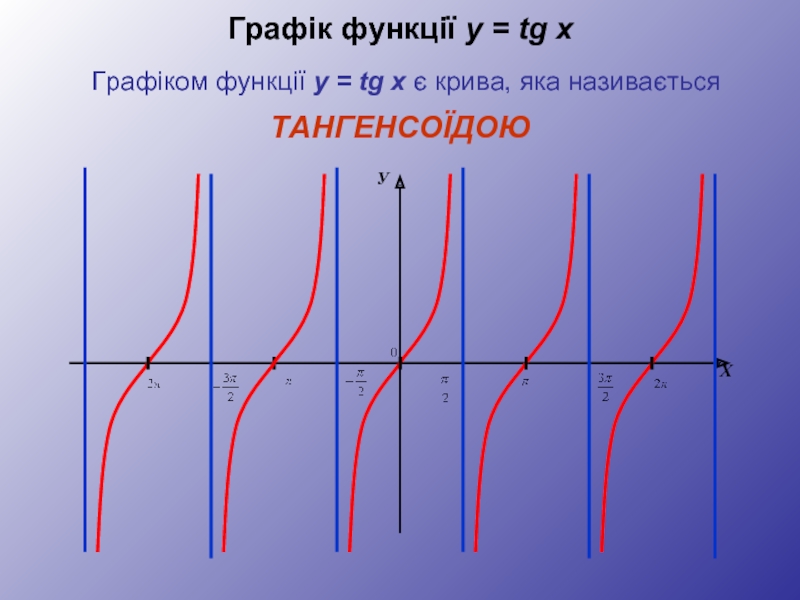
- 25. Графік функції y = tg x
- 27. Побудувати графік функції y = tg x
- 28. У Х Побудувати графік функції y
- 29. У Х Побудувати графік функції
- 30. y
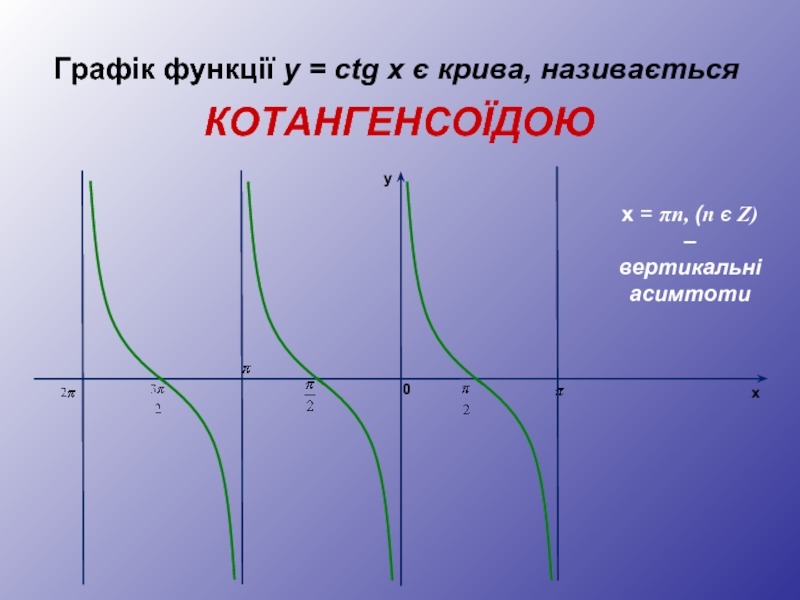
- 31. Графік функції y = сtg x є
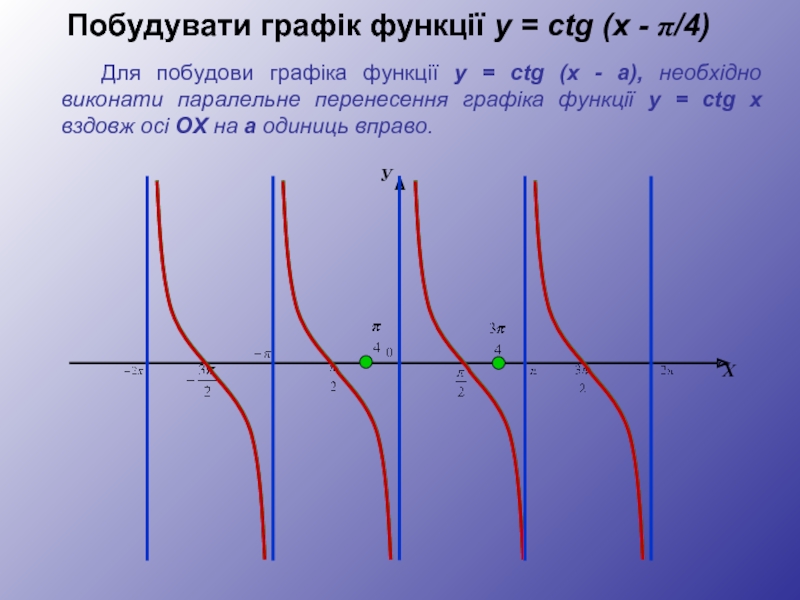
- 32. Побудувати графік функції y = сtg (x
- 33. У Х Побудувати графік функції y =
- 34. Рефлексія: 1) Вам було на уроці:
Слайд 2Практичне застосування тригонометричних функцій
Синусоїда – хвилеподібна плоска крива, яка є графіком
Слайд 3Зміна будь-якої величини за законом синуса називається гармонійним коливанням. Приклади таких
Практичне застосування тригонометричних функцій
Ще один приклад синусоїдальних коливань – звук (гармонійне коливання повітря), що відповідає коливанню y = A*sin ωt
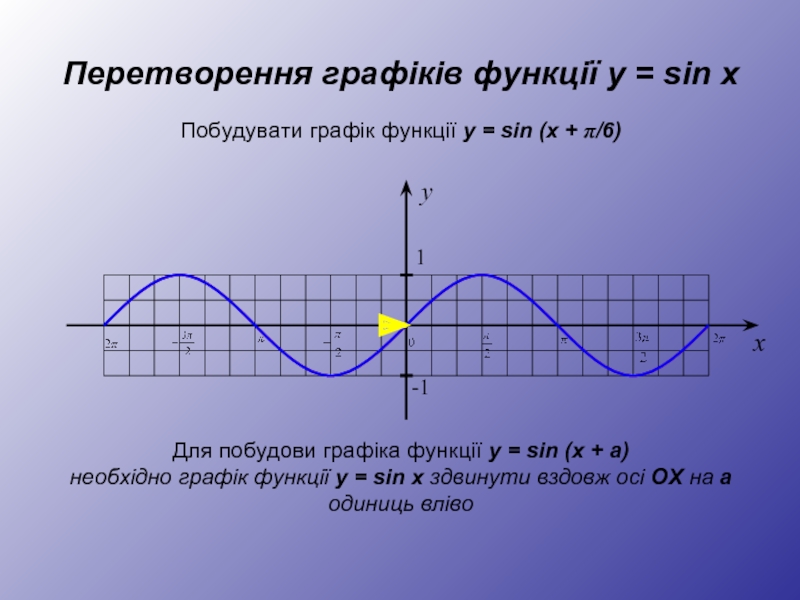
Слайд 7Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
Для побудови графіка функції y = sin (x + а)
необхідно графік функції y = sin x здвинути вздовж осі OX на а одиниць вліво
Слайд 8Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
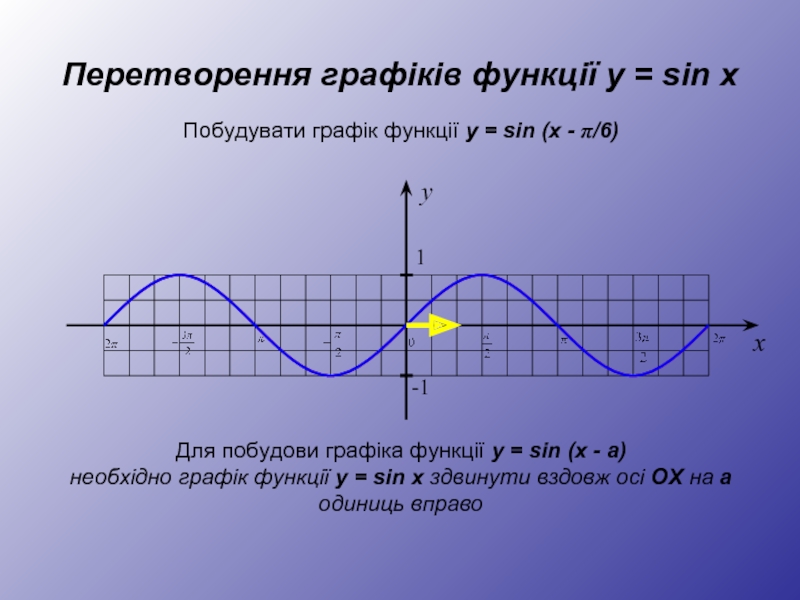
Для побудови графіка функції y = sin (x - а)
необхідно графік функції y = sin x здвинути вздовж осі OX на а одиниць вправо
Слайд 9Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
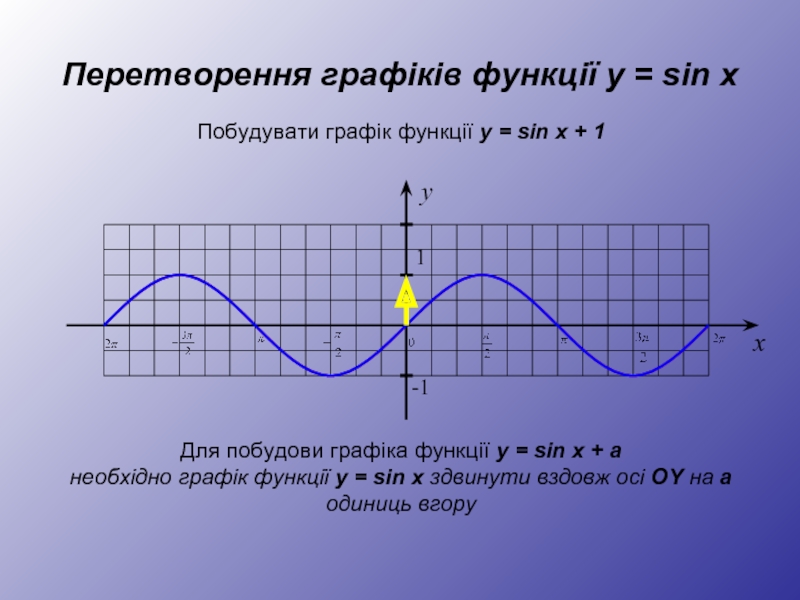
Для побудови графіка функції y = sin x + а
необхідно графік функції y = sin x здвинути вздовж осі OY на а одиниць вгору
Слайд 10Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
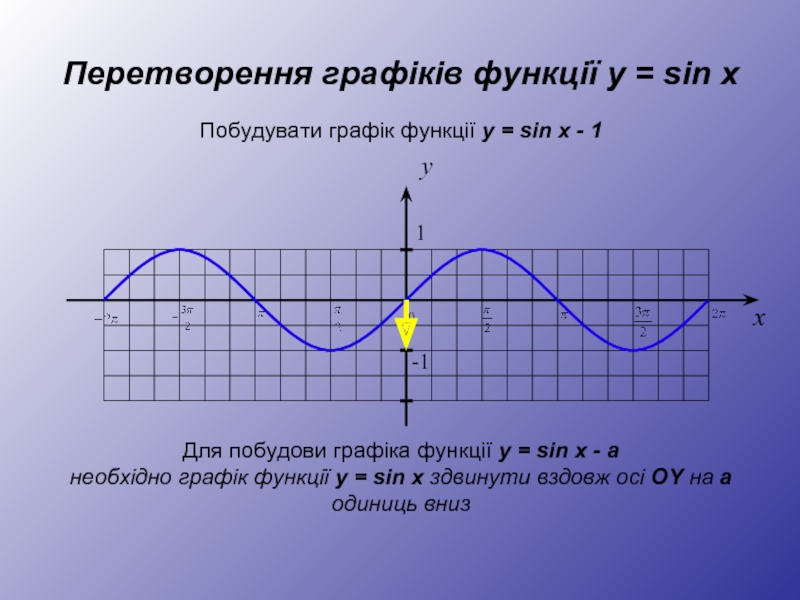
Для побудови графіка функції y = sin x - а
необхідно графік функції y = sin x здвинути вздовж осі OY на а одиниць вниз
Слайд 11Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
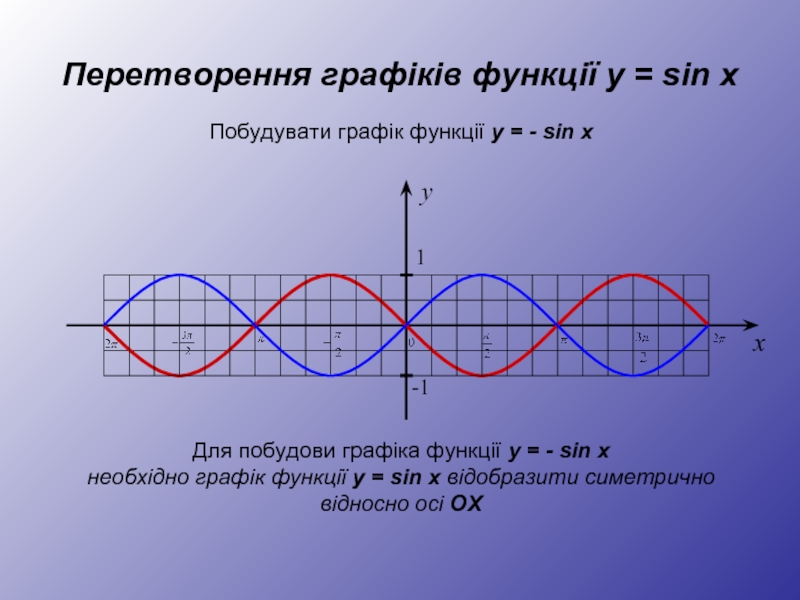
Для побудови графіка функції y = - sin x
необхідно графік функції y = sin x відобразити симетрично відносно осі OX
Слайд 12Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
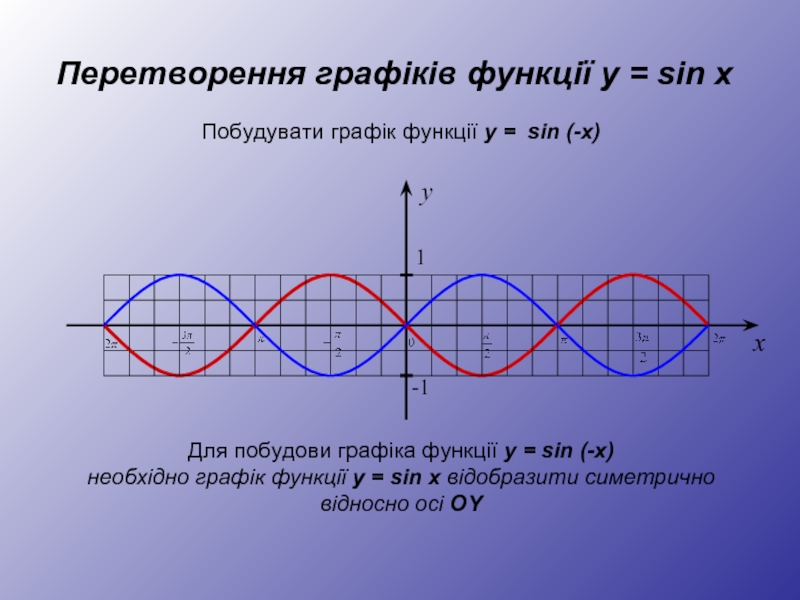
Для побудови графіка функції y = sin (-x)
необхідно графік функції y = sin x відобразити симетрично відносно осі OY
Слайд 13Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
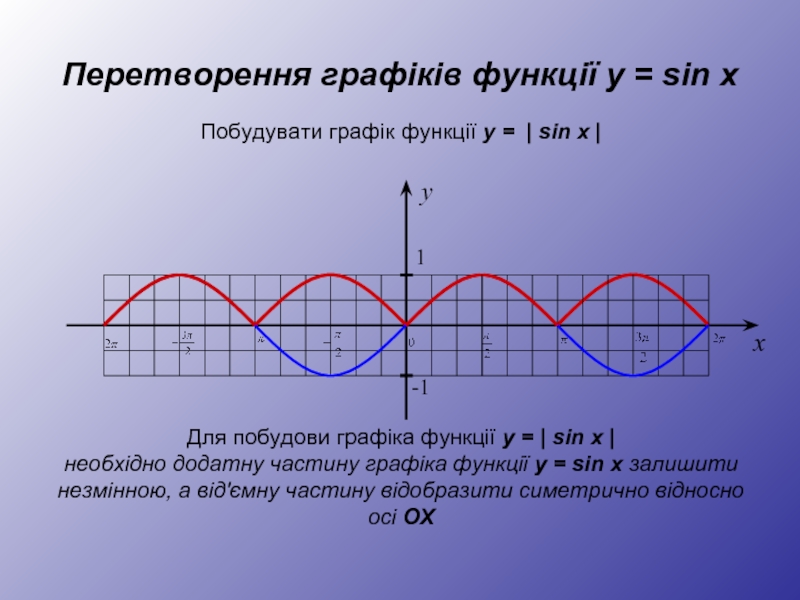
Для побудови графіка функції y = | sin x |
необхідно додатну частину графіка функції y = sin x залишити незмінною, а від'ємну частину відобразити симетрично відносно осі OX
Слайд 14Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
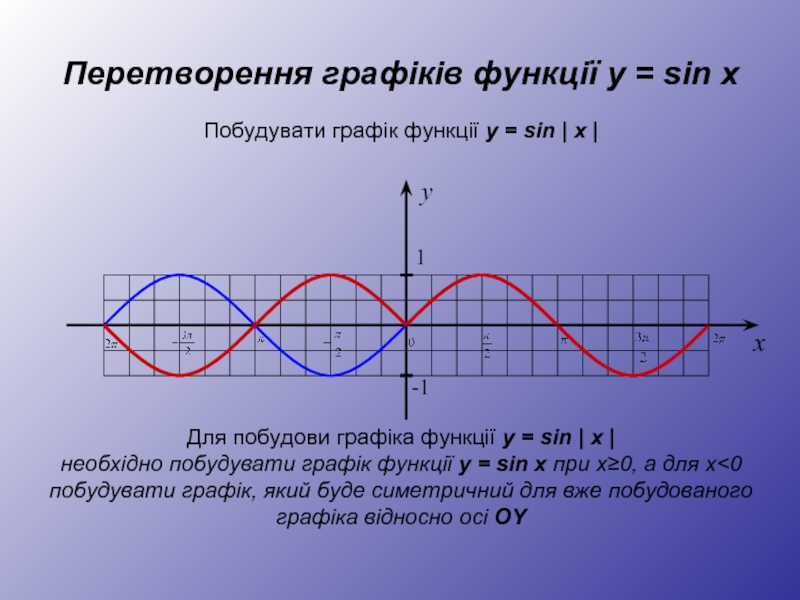
Для побудови графіка функції y = sin | x |
необхідно побудувати графік функції y = sin x при x≥0, а для x<0 побудувати графік, який буде симетричний для вже побудованого графіка відносно осі OY
Слайд 15Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
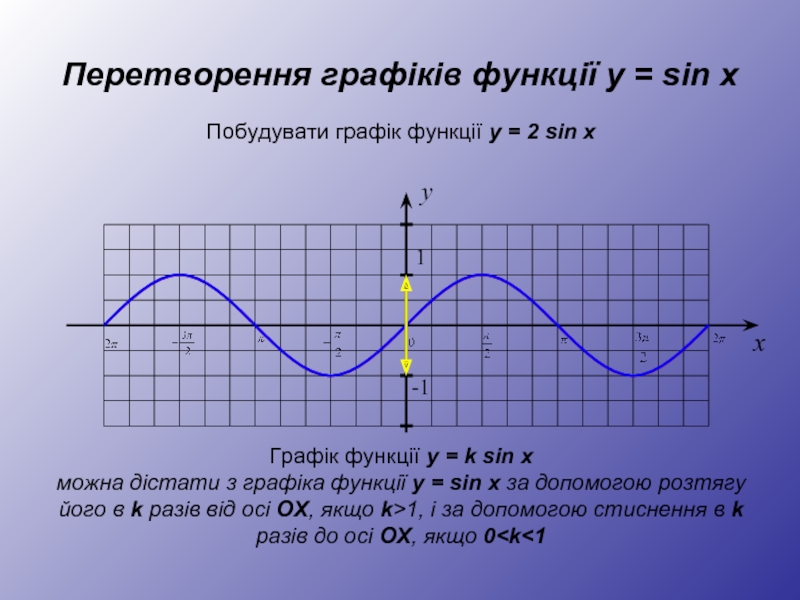
Графік функції y = k sin x
можна дістати з графіка функції y = sin x за допомогою розтягу його в k разів від осі OX, якщо k>1, і за допомогою стиснення в k разів до осі OX, якщо 0
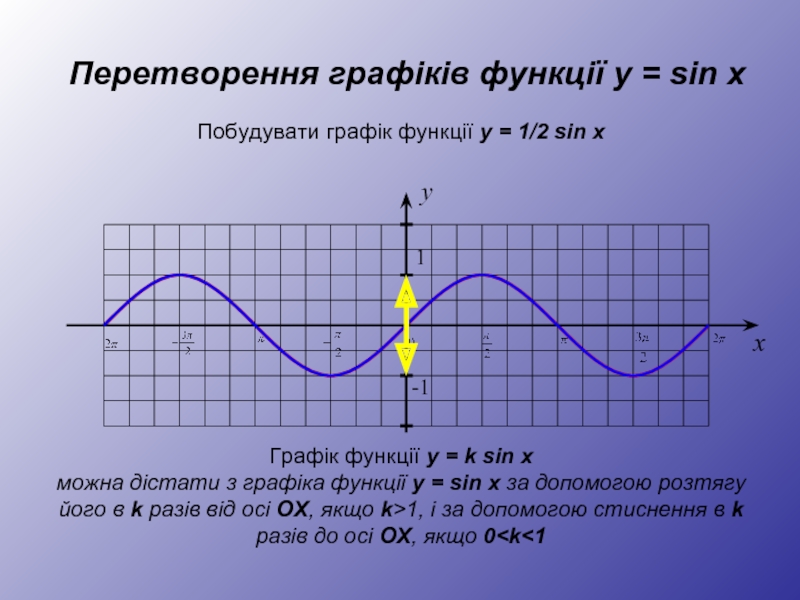
Слайд 16Перетворення графіків функції y = sin x
y
1
-1
x
Побудувати графік функції y =
Графік функції y = k sin x
можна дістати з графіка функції y = sin x за допомогою розтягу його в k разів від осі OX, якщо k>1, і за допомогою стиснення в k разів до осі OX, якщо 0
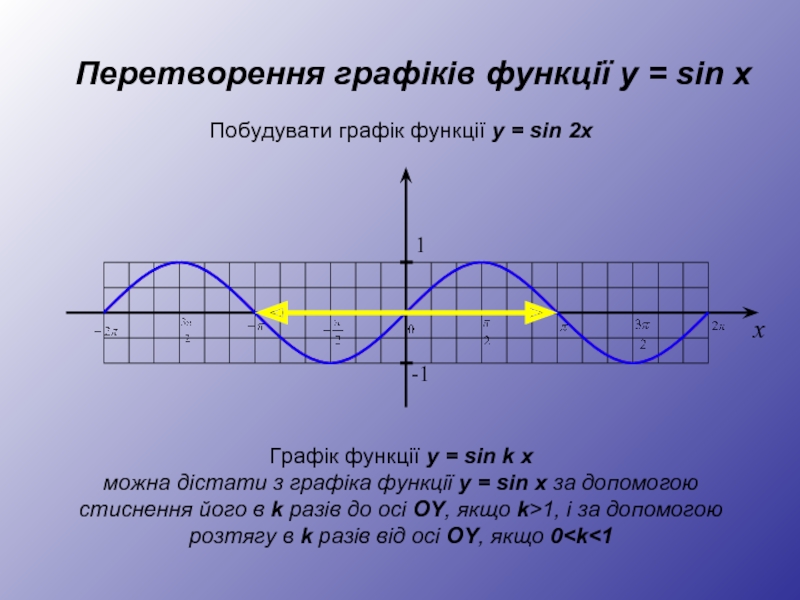
Слайд 17Перетворення графіків функції y = sin x
Побудувати графік функції y =
Графік функції y = sin k x
можна дістати з графіка функції y = sin x за допомогою стиснення його в k разів до осі OY, якщо k>1, і за допомогою розтягу в k разів від осі OY, якщо 0 1 -1 x
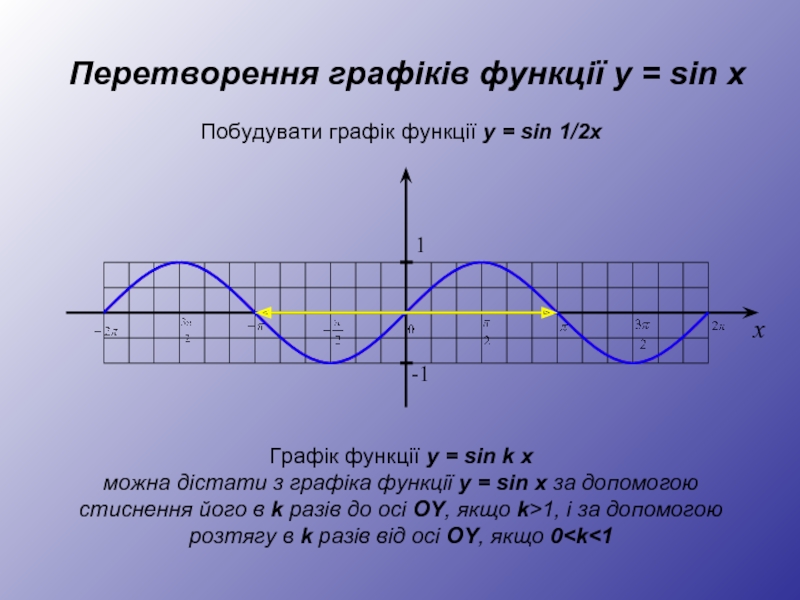
Слайд 18Перетворення графіків функції y = sin x
Побудувати графік функції y =
Графік функції y = sin k x
можна дістати з графіка функції y = sin x за допомогою стиснення його в k разів до осі OY, якщо k>1, і за допомогою розтягу в k разів від осі OY, якщо 0 1 -1 x
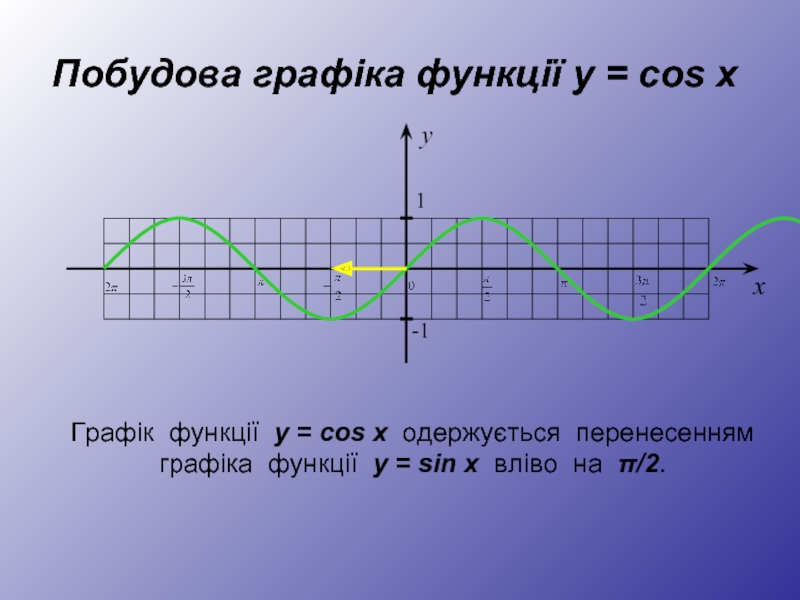
Слайд 20Побудова графіка функції y = cos x
Графік функції у = cos
графіка функції у = sin x вліво на π/2.
Слайд 22Перетворення графіків функції y = cos x
Перетворення графіків функції y =
Слайд 23y
1
-1
x
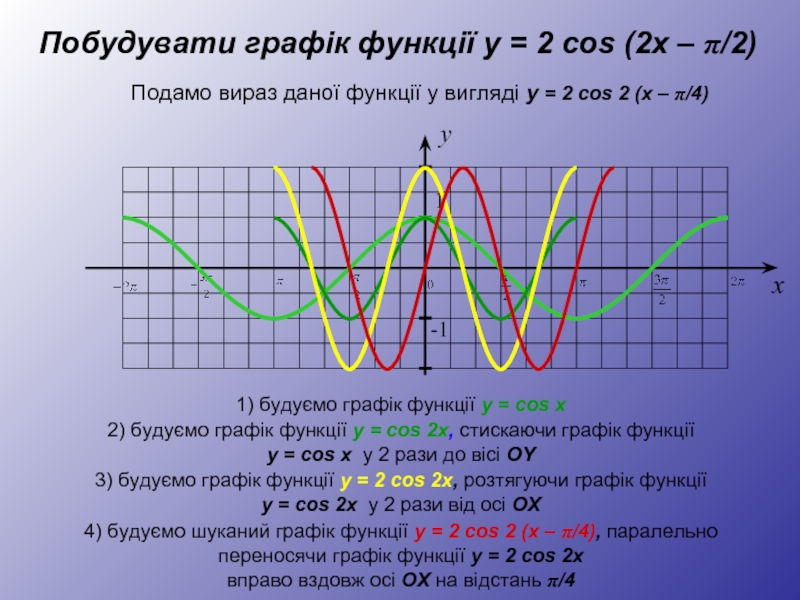
Побудувати графік функції y = 2 cos (2x – π/2)
1) будуємо
2) будуємо графік функції y = cos 2x, стискаючи графік функції
y = cos x у 2 рази до вісі OY
3) будуємо графік функції y = 2 cos 2x, розтягуючи графік функції
y = cos 2x у 2 рази від осі OX
4) будуємо шуканий графік функції y = 2 cos 2 (x – π/4), паралельно переносячи графік функції y = 2 cos 2x
вправо вздовж осі OX на відстань π/4
Подамо вираз даної функції у вигляді y = 2 cos 2 (x – π/4)
Слайд 24х
у
1
0
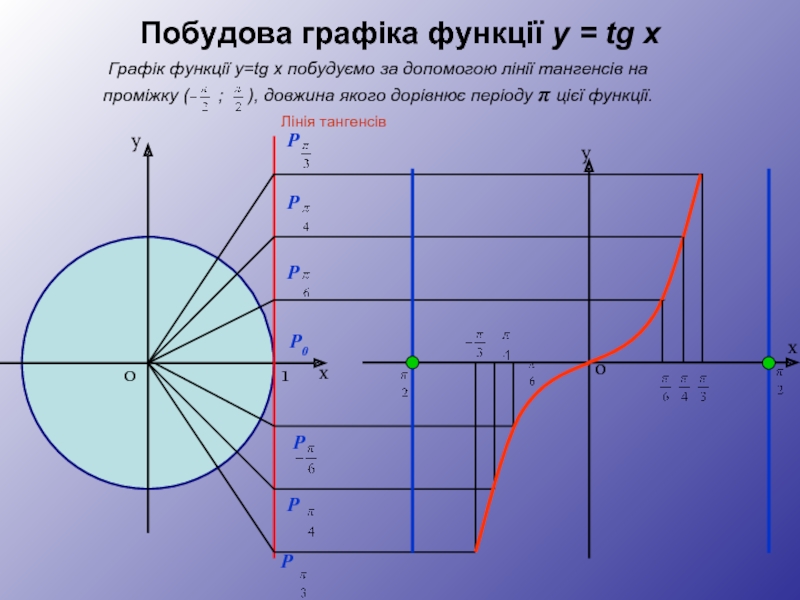
Лінія тангенсів
х
0
у
P0
P
P
P
P
P
P
Побудова графіка функції y = tg x
Графік функції y=tg
Слайд 26
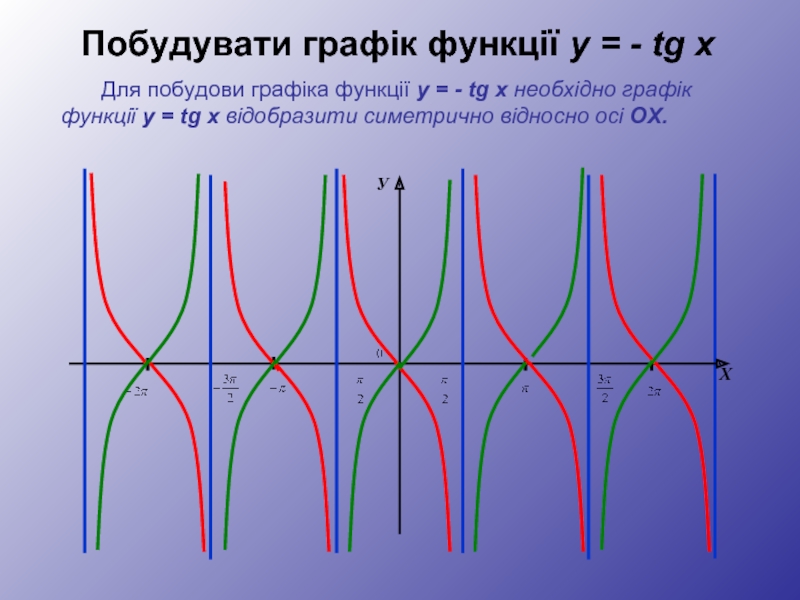
Побудувати графік функції y = - tg x
Для побудови графіка функції
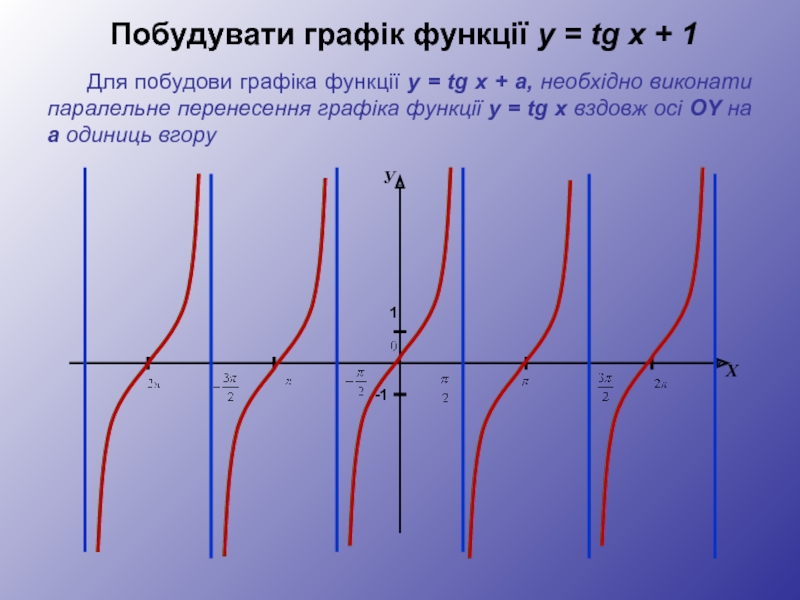
Слайд 27Побудувати графік функції y = tg x + 1
Для побудови графіка
Слайд 28У
Х
Побудувати графік функції y = Іtg xІ
Для побудови графіка функції y
Слайд 29
У
Х
Побудувати графік функції y = tg | x |
Для побудови графіка
Слайд 30
y
x
0
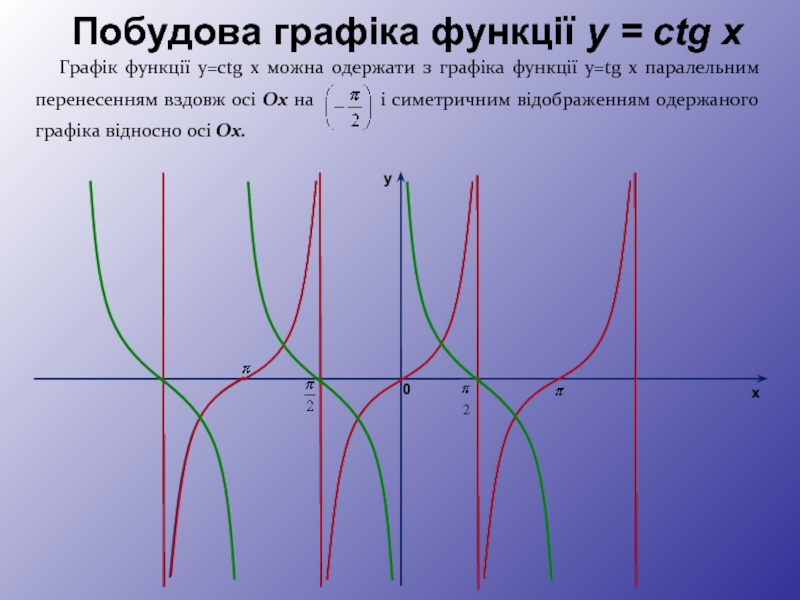
Графік функції y=ctg x можна одержати з графіка функції y=tg x
Побудова графіка функції y = ctg x
Слайд 31Графік функції y = сtg x є крива, називається
КОТАНГЕНСОЇДОЮ
y
x
0
х = πn,
Слайд 32Побудувати графік функції y = сtg (x - π/4)
Для побудови графіка
Слайд 33У
Х
Побудувати графік функції y = - сtg x
Для побудови графіка функції
Слайд 34Рефлексія:
1) Вам було на уроці:
ЛЕГКО;
ВАЖКО;
ЗВИЧНО.
2) Що вам було не зрозуміло
