- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площадь криволинейной трапеции и интеграл презентация
Содержание
- 1. Площадь криволинейной трапеции и интеграл
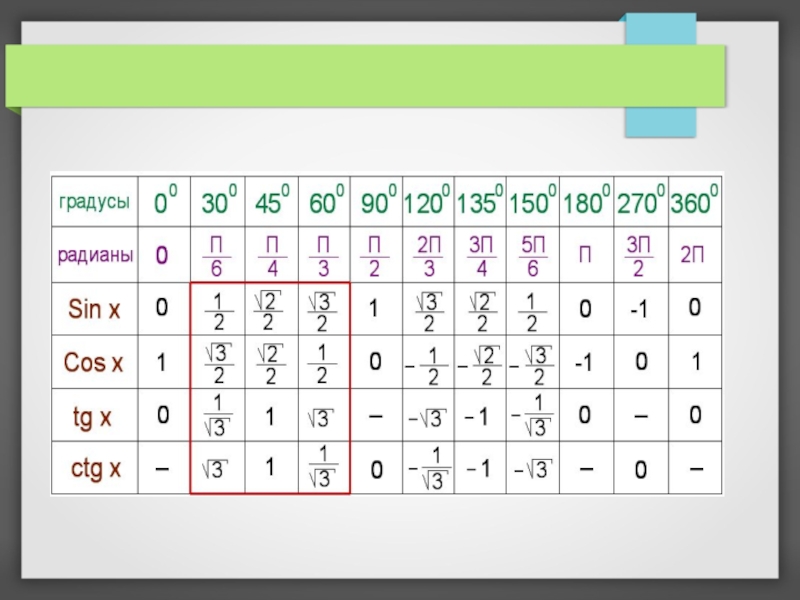
- 2. Найти первообразную функции:
- 3. a b х=а x=b
- 4. Площадь криволинейной трапеции.
- 5. Формула Ньютона-Лейбница 1643—1727 1646—1716
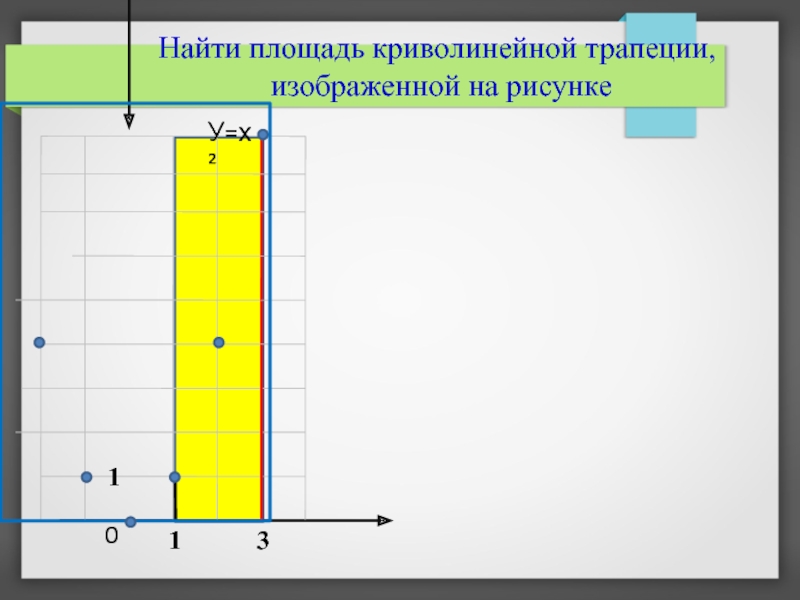
- 6. Найти площадь криволинейной трапеции, изображенной
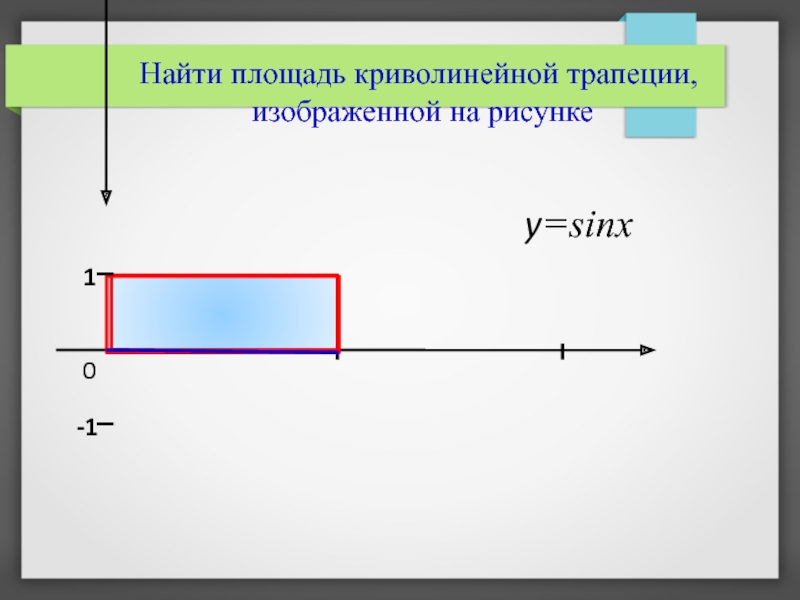
- 7. Найти площадь криволинейной трапеции, изображенной
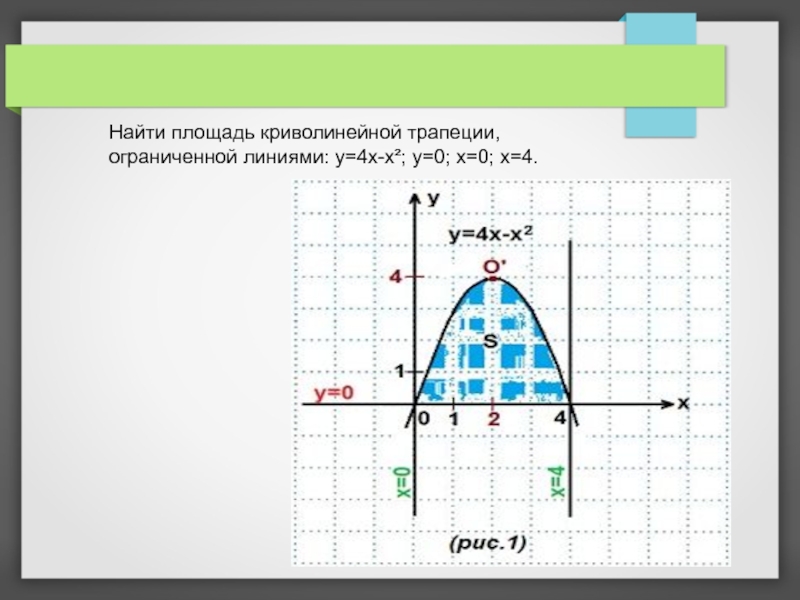
- 9. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.
- 10. Решение. Строим графики данных линий. 1)
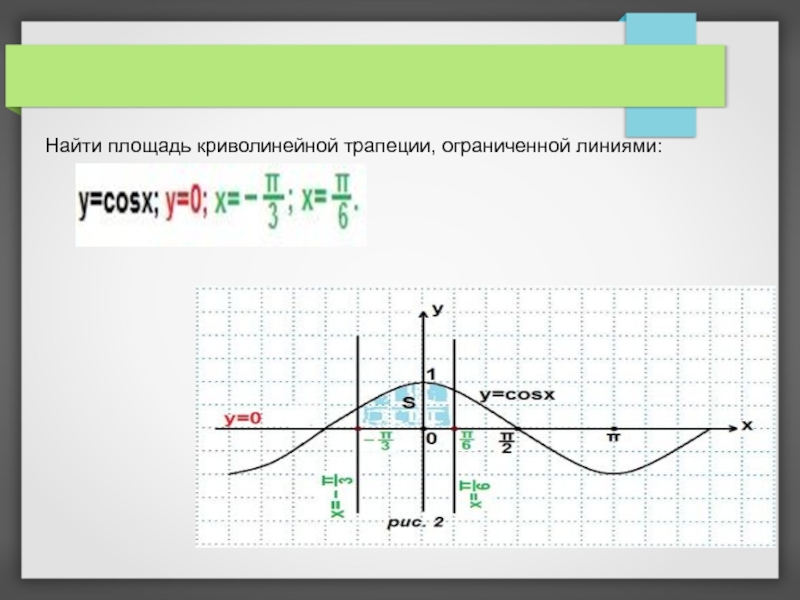
- 11. Найти площадь криволинейной трапеции, ограниченной линиями:
- 12. Решение:
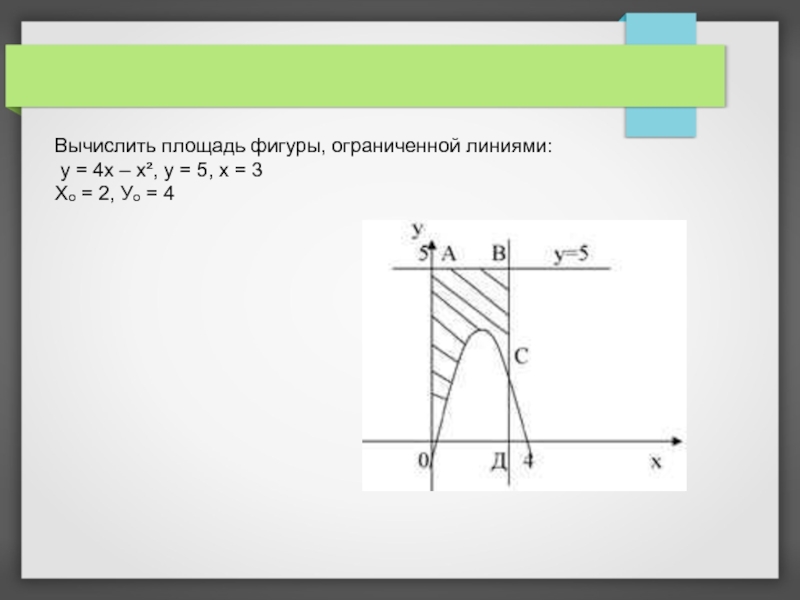
- 13. Вычислить площадь фигуры, ограниченной линиями: у
- 14. Sф = S(ОАВД) – S(ОСД) Sпрям.
Слайд 3
a
b
х=а
x=b
0
y = f(x)
Х
У
Криволинейная трапеция
Отрезок [a;b] называют основанием
этой криволинейной
трапеции
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
Слайд 10Решение. Строим графики данных линий.
1) y=4x-x² — парабола (вида y=ax²+bx+c).
Запишем данное уравнение
в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз,
так как первый коэффициент а=-1<0.
Вершина параболы находится
в точке O′(m; n), где
О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:
4х-х²=0.
Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4.
Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).
2) y=0 — это ось Ох;
3) х=0 — это ось Оy;
4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных
отрезка вправо.
Площадь построенной криволинейной трапеции находим по (ф. Н-Л).
У нас f (x)=4x-x², a=0, b=4.
в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз,
так как первый коэффициент а=-1<0.
Вершина параболы находится
в точке O′(m; n), где
О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:
4х-х²=0.
Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4.
Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).
2) y=0 — это ось Ох;
3) х=0 — это ось Оy;
4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных
отрезка вправо.
Площадь построенной криволинейной трапеции находим по (ф. Н-Л).
У нас f (x)=4x-x², a=0, b=4.
Слайд 14Sф = S(ОАВД) – S(ОСД)
Sпрям. =
S(ОСД) = F(3) – F(0),
где F(x) первообразная для функции
f(х) = 4х – х²
F(х)= ; SОСД=
Sф = 15 – 9 = 6.
![ab х=аx=b0y = f(x)ХУКриволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура, ограниченная](/img/tmb/4/325700/2446f63f15d58d17eb10c46efda87128-800x.jpg)