- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пирамиды в нашей жизни презентация
Содержание
- 1. Пирамиды в нашей жизни
- 2. Пирамиды в нашей жизни Теория Виды пирамид Применение теории в задачах Содержание:
- 3. Пирамида Хеопса (Хуфу), Великая пирамида Гизы —
- 4. В Японии появился жилой дом в форме
- 5. Пирамидой называется многогранник, который состоит из плоского
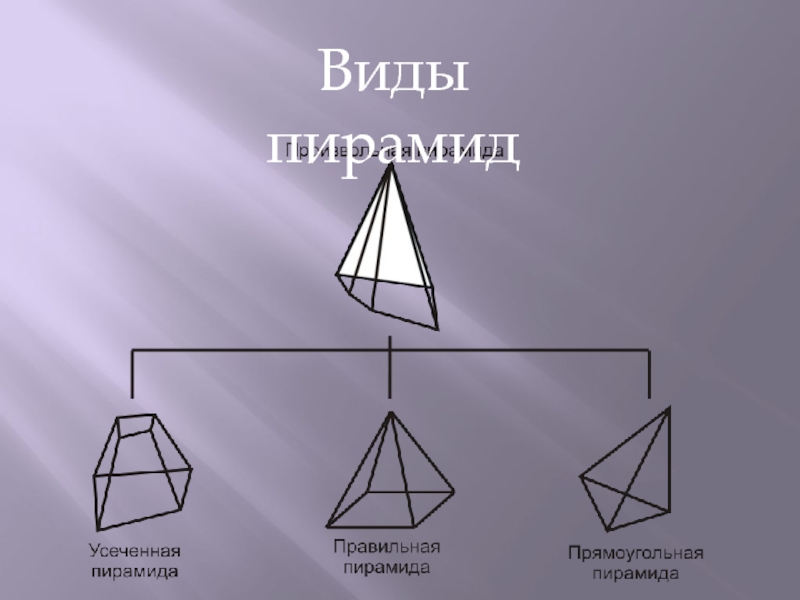
- 6. Виды пирамид
- 7. Задача 1 Дано: SABCD - пирамида;
- 8. https://ru.wikipedia.org/wiki/%D0%9F%D0%B8%D1%80%D0%B0%D0%BC%D0%B8%D0%B4%D0%B0_%D0%A5%D0%B5%D0%BE%D0%BF%D1%81%D0%B0 http://www.novate.ru/blogs/150709/12489/ http://compendium.su/mathematics/geometry10/52.html http://files.school-collection.edu.ru/dlrstore/867ea11e-0927-11dc-a9bd-ddc28aa48d0a/word.html Ссылки на используемый материал
Слайд 3Пирамида Хеопса (Хуфу), Великая пирамида Гизы — крупнейшая из египетских пирамид,
Пирамида Хеопса
Слайд 4В Японии появился жилой дом в форме пирамиды. Пирамида - одна
Дом-пирамида в Японии
Слайд 5Пирамидой называется многогранник, который состоит из плоского многоугольника — основания пирамиды,
Теория
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.
Высота боковой грани, проведенная из ее вершины, называется апофемой.
Слайд 7Задача 1
Дано: SABCD - пирамида; ABCD - ромб;
АВ =
Найти: AS. Решение:
Задачи
Пусть SABCD - данная пирамида. ABCD - ромб (по условию задачи). Точка пересечения диагоналей является центром ромба ABCD. О - центр ромба. Следовательно, пирамида является правильной.
По свойству диагоналей ромба: DO = ВО = 4 см.
Из ΔASO, по теореме Пифагора, имеем:
SA = SC, как наклонные, имеющие одинаковые проекции. Аналогично из ΔSDO по теореме Пифагора имеем:
SB = SD - как наклонные, имеющие одинаковые проекции.