- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Первый признак равенства треугольников. (7 класс) презентация
Содержание
- 1. Первый признак равенства треугольников. (7 класс)
- 2. Цели: 19.09.2012 Ввести понятие теоремы и доказательства
- 3. 19.09.2012 www.konspekturoka.ru Вспомним! Устно. Задача ∆АPC
- 4. 19.09.2012 www.konspekturoka.ru Вспомним! Устно. Задача ∆АВC
- 5. 19.09.2012 www.konspekturoka.ru Задача АВ = АС =
- 6. 19.09.2012 www.konspekturoka.ru Какие условия должны выполняться для
- 7. 19.09.2012 www.konspekturoka.ru Не нужно проверять равенство всех
- 8. 19.09.2012 www.konspekturoka.ru Доказывать признаки нужно с помощью
- 9. 19.09.2012 www.konspekturoka.ru Первый признак равенства треугольников (по
- 10. Теорема: 1 2 (условие) ∆АВC,
- 11. 19.09.2012 www.konspekturoka.ru Два треугольника называются равными, если
- 12. 19.09.2012 www.konspekturoka.ru Задача Отрезки АЕ и
- 13. 19.09.2012 Ответить на вопросы: Что такое теорема
Слайд 1Треугольники
7 класс
геометрия
Урок № 12
Первый признак равенства треугольников
19.09.2012
www.konspekturoka.ru
Слайд 2Цели:
19.09.2012
Ввести понятие теоремы и доказательства теоремы;
Доказать первый признак равенства треугольников;
Научить решать
www.konspekturoka.ru
Слайд 319.09.2012
www.konspekturoka.ru
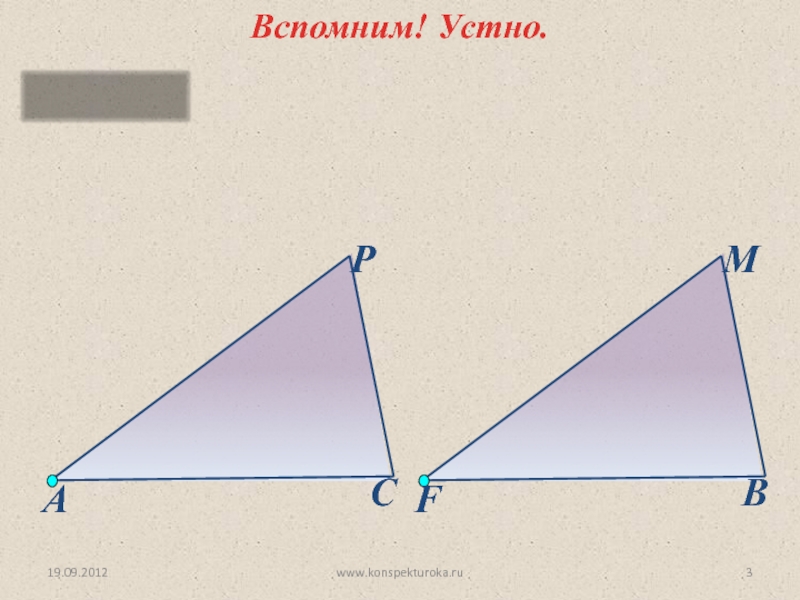
Вспомним! Устно.
Задача
∆АPC = ∆ FMB, ∠P = ∠M, ∠A =
АС и МВ.
1
23 см.
17см
?
?
Слайд 419.09.2012
www.konspekturoka.ru
Вспомним! Устно.
Задача
∆АВC = ∆ ADC, ∠ABC = 70°, AB =
2
∠MDC, AD.
А
D
C
B
M
?
?
10см.
70°
Слайд 519.09.2012
www.konspekturoka.ru
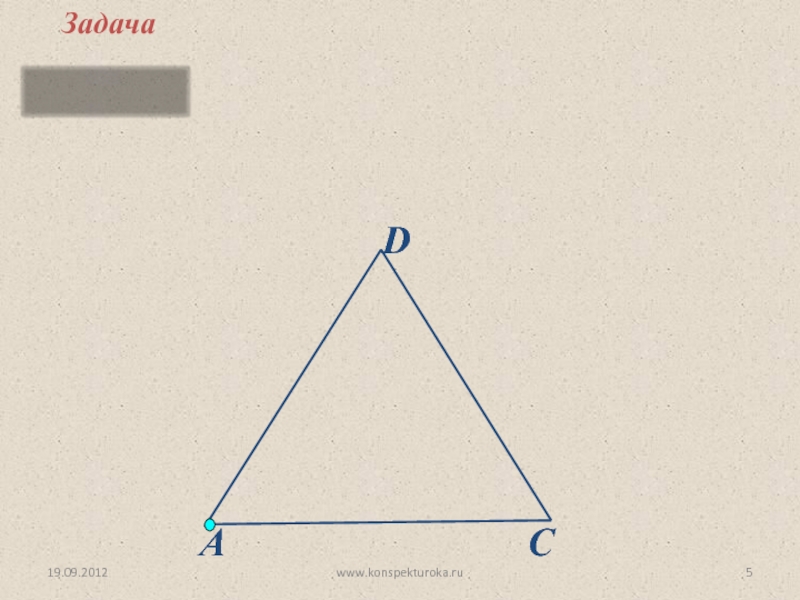
Задача
АВ = АС = ВС, АD = DC,
P₁ = 36
стороны ∆АВС и ∆ АDС.
Вспомним! Устно.
3
Слайд 619.09.2012
www.konspekturoka.ru
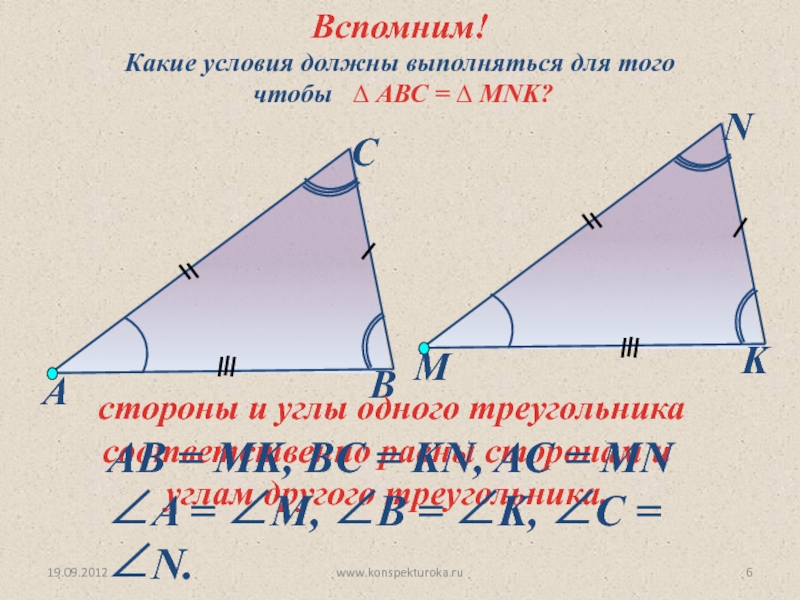
Какие условия должны выполняться для того
чтобы ∆ АВС
стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника.
Вспомним!
АВ = MK, BС = KN, AC = MN
∠A = ∠M, ∠B = ∠K, ∠C = ∠N.
Слайд 719.09.2012
www.konspekturoka.ru
Не нужно проверять равенство всех
сторон и углов!
Достаточно сравнить лишь
элемента одного треугольника с
тремя элементами другого
треугольника.
Какие три элементы?
О том, какие три элемента расскажут признаки равенства
треугольников.
Слайд 819.09.2012
www.konspekturoka.ru
Доказывать признаки нужно с помощью теоремы
(утверждение, справедливость
которого устанавливается
Сами рассуждения называются доказательством теоремы.
Любая теорема состоит из условия
и заключения.
Условие – это уже известные факты, о которых
говорится в теореме, а заключение – это то, что
нужно получить, доказать.
Слайд 919.09.2012
www.konspekturoka.ru
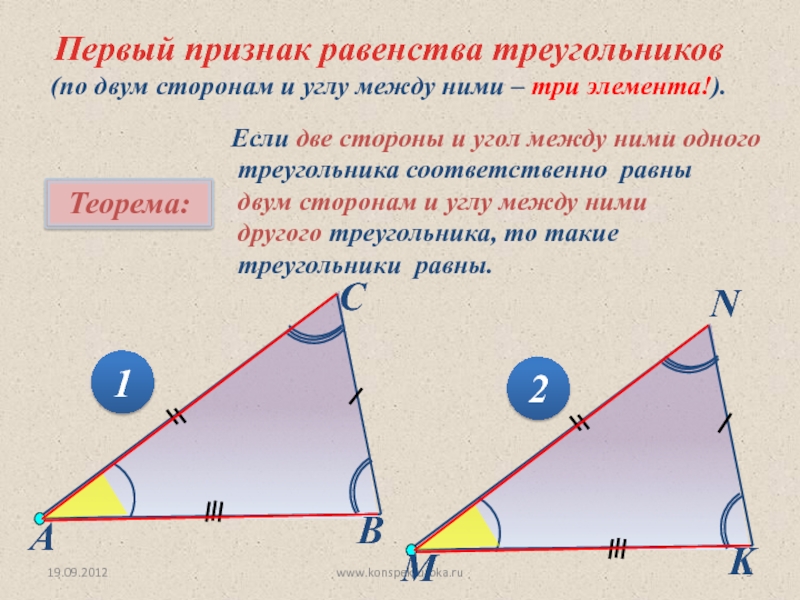
Первый признак равенства треугольников
(по двум сторонам и углу между ними –
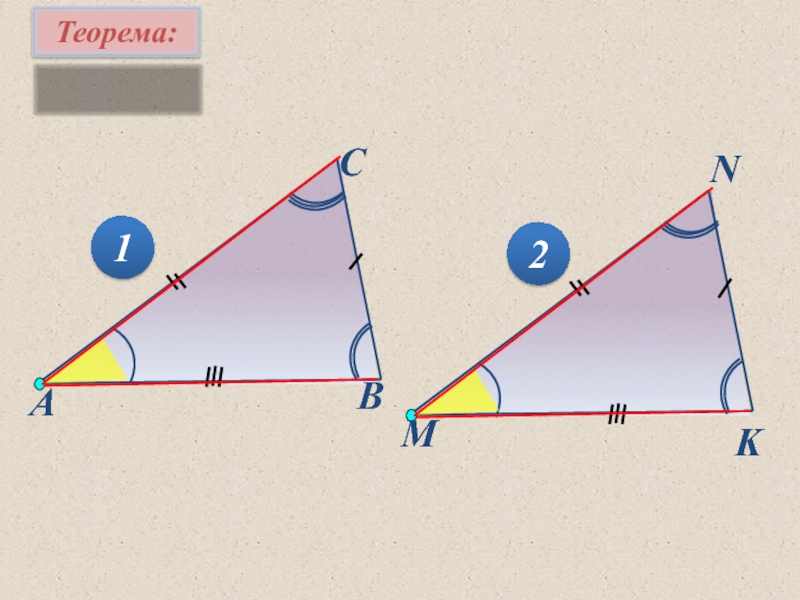
Теорема:
Если две стороны и угол между ними одного
треугольника соответственно равны
двум сторонам и углу между ними
другого треугольника, то такие
треугольники равны.
1
2
Слайд 10Теорема:
1
2
(условие) ∆АВC, ∆А₁В₁С ₁, АВ = А₁В₁,
АС = А₁С₁, ∠А
(заключение) ∆АВC = ∆А₁В₁С ₁,
Доказательство.
Так как ∠А =∠А₁, то ∆АВC можно наложить на ∆А₁В₁С ₁ так, что вершина А совместится с вершиной А₁.
Слайд 1119.09.2012
www.konspekturoka.ru
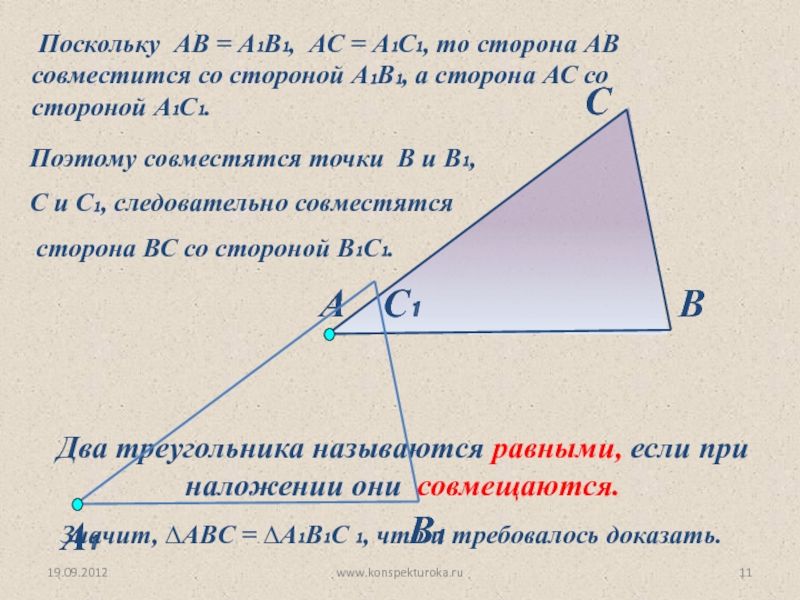
Два треугольника называются равными, если при наложении они совмещаются.
А
В
С
Поэтому совместятся точки В и В₁,
С и С₁, следовательно совместятся
сторона ВС со стороной В₁С₁.
Значит, ∆АВC = ∆А₁В₁С ₁, что и требовалось доказать.
Слайд 12
19.09.2012
www.konspekturoka.ru
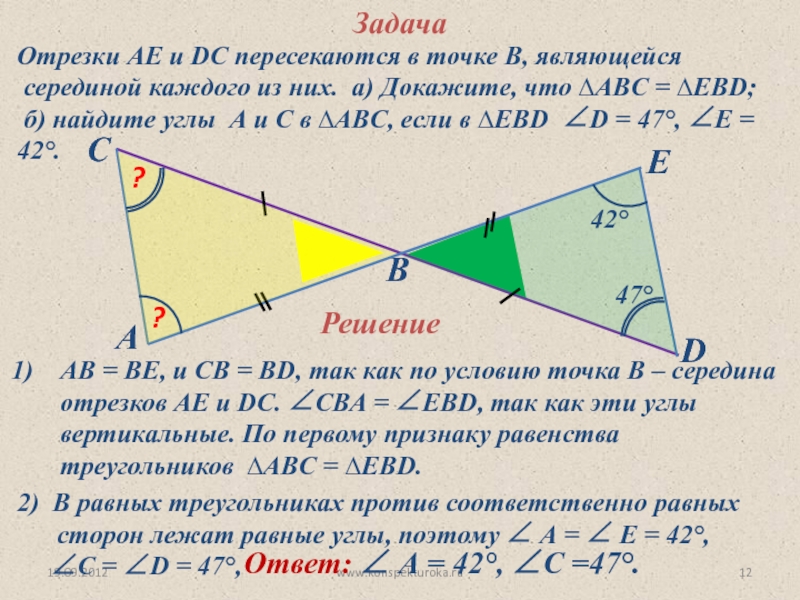
Задача
Отрезки АЕ и DC пересекаются в точке В, являющейся
серединой
б) найдите углы А и С в ∆АВC, если в ∆ЕВD ∠D = 47°, ∠E = 42°.
Решение
A
C
B
E
D
?
42°
47°
АВ = ВЕ, и СВ = ВD, так как по условию точка В – середина отрезков АЕ и DC. ∠СВА = ∠ЕВD, так как эти углы вертикальные. По первому признаку равенства треугольников ∆АВC = ∆ЕВD.
2) В равных треугольниках против соответственно равных
сторон лежат равные углы, поэтому ∠ А = ∠ Е = 42°,
∠С = ∠D = 47°,
Ответ: ∠ А = 42°, ∠С =47°.
?
Слайд 1319.09.2012
Ответить на вопросы:
Что такое теорема и доказательство теоремы?
Сформулировать первый признак равенства
Доказать теорему, выражающую первый признак равенства треугольников.
www.konspekturoka.ru
Спасибо за внимание!