Тема 6
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов презентация
Содержание
- 1. Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов
- 2. Вопросы темы Понятие первообразной. Неопределенный интеграл и его свойства. Таблица основных интегралов.
- 3. ПОНЯТИЕ ПЕРВООБРАЗНОЙ
- 4. Определение Функция F(x) называется первообразной функцией для
- 5. Геометрический смысл первообразной Геометрический смысл производной: F’(x)
- 6. Теорема Если F1(x) и F2(x) – первообразные
- 7. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
- 8. Определение Совокупность всех первообразных для функции f(x)
- 9. Свойства неопределенного интеграла Производная от неопределенного интеграла равна подынтегральной функции:
- 10. Свойства неопределенного интеграла Дифференциал неопределенного интеграла равен подынтегральному выражению:
- 11. Свойства неопределенного интеграла Неопределенный интеграл от
- 12. Свойства неопределенного интеграла Постоянный множитель можно выносить за знак интеграла:
- 13. Свойства неопределенного интеграла Интеграл от алгебраической
- 14. ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
- 16. НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
- 17. Если , то:
- 18. СПЕЦИАЛЬНЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
- 19. Интегрирование методом замены переменной (метод подстановки) Пусть
- 20. Методы замены переменной Если в подынтегральной функции
- 21. Методы замены переменной Замену переменной можно осуществлять
- 22. Интегрирование по частям Пусть u(x) и v(x)
- 23. Сведение интеграла «к самому себе» С
- 24. Рекуррентные соотношения Если подынтегральная функция зависит от
- 25. «Неберущиеся» интегралы Производная элементарной функции также является
Слайд 1Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов
ЛЕКЦИЯ
Калабухова
Галина Валентиновна
кандидат социологических
Слайд 2Вопросы темы
Понятие первообразной.
Неопределенный интеграл и его свойства.
Таблица основных интегралов.
Слайд 4Определение
Функция F(x) называется первообразной функцией для функции f(x) на промежутке X,
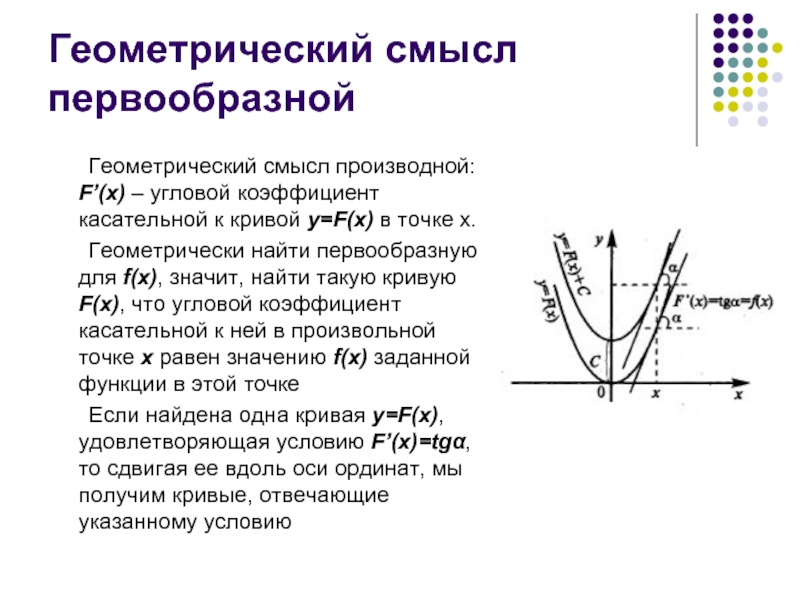
Слайд 5Геометрический смысл первообразной
Геометрический смысл производной: F’(x) – угловой коэффициент касательной к
Геометрически найти первообразную для f(x), значит, найти такую кривую F(x), что угловой коэффициент касательной к ней в произвольной точке x равен значению f(x) заданной функции в этой точке
Если найдена одна кривая y=F(x), удовлетворяющая условию F’(x)=tgα, то сдвигая ее вдоль оси ординат, мы получим кривые, отвечающие указанному условию
Слайд 6Теорема
Если F1(x) и F2(x) – первообразные для функции f(x) на промежутке
Слайд 8Определение
Совокупность всех первообразных для функции f(x) на промежутке X, называется неопределенным
f(x) – подынтегральная функция
f(x)dx – подынтегральное выражение
F(x) – некоторая первообразная для f(x)
C – произвольная константа
Слайд 9Свойства
неопределенного интеграла
Производная от неопределенного интеграла равна подынтегральной функции:
Слайд 10Свойства
неопределенного интеграла
Дифференциал неопределенного интеграла равен подынтегральному выражению:
Слайд 11Свойства
неопределенного интеграла
Неопределенный интеграл от дифференциала некоторой функции равен этой функции
Слайд 13Свойства
неопределенного интеграла
Интеграл от алгебраической суммы двух функций равен такой же
Слайд 19Интегрирование методом замены переменной (метод подстановки)
Пусть ,
тогда:
где t(x) - дифференцируемая
Слайд 20Методы замены переменной
Если в подынтегральной функции удаётся сразу заметить оба сомножителя,
Слайд 21Методы замены переменной
Замену переменной можно осуществлять формальным сведением подынтегрального выражения к
Слайд 22Интегрирование по частям
Пусть u(x) и v(x) - функции, имеющие непрерывные частные
d(uv) = u∙dv + v∙du → u∙dv = d(uv) - v∙du.
Находим неопределённые интегралы для обеих частей этого равенства (при этом ):
Или:
Слайд 23Сведение интеграла
«к самому себе»
С помощью интегрирования по частям (возможно, неоднократного)
Слайд 24Рекуррентные соотношения
Если подынтегральная функция зависит от некоторого параметра n, и получено
Слайд 25«Неберущиеся» интегралы
Производная элементарной функции также является элементарной функцией. При нахождении первообразной
Соответствующие интегралы называются неберущимися в элементарных функциях, в сами функции – неинтегрируемыми в конечном виде