Первообразная и интеграл презентация

Содержание

1. Первообразная и интеграл
2. Первообразная
7. Понятие первообразной Функцию F(x) называют первообразной для
9. Примеры f(x) = 2x; F(x) =
10. Правила отыскания первообразных
15. Таблица первообразных f(x) F(x) F(x)
16. Неопределенный интеграл Неопределенным интегралом от непрерывной на
17. Примеры
18. Определенный интеграл – формула Ньютона-Лейбница. Геометрический смысл
19. Вычисление определенного интеграла
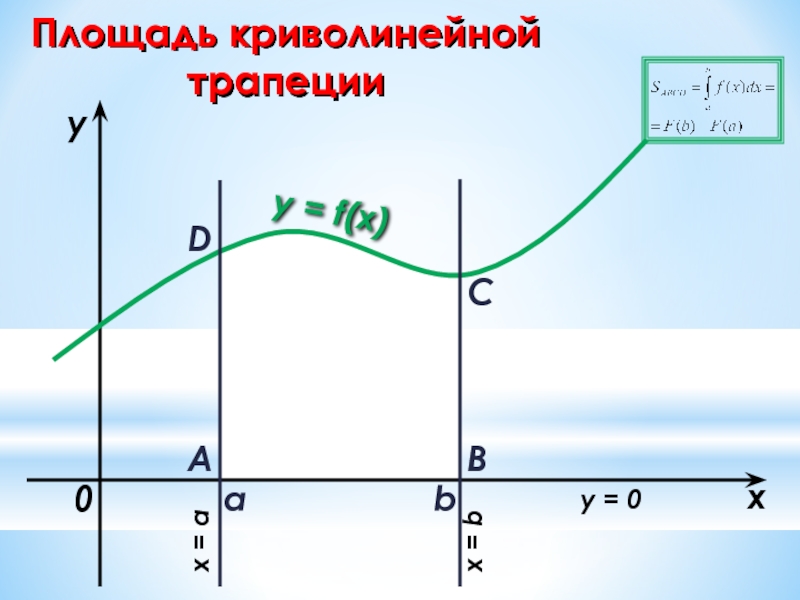
20. Площадь криволинейной трапеции a
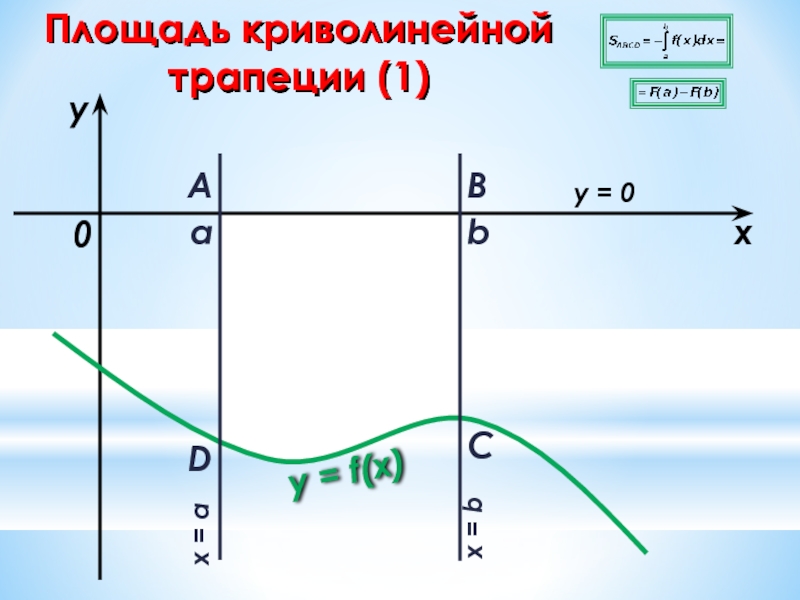
21. Площадь криволинейной трапеции (1)
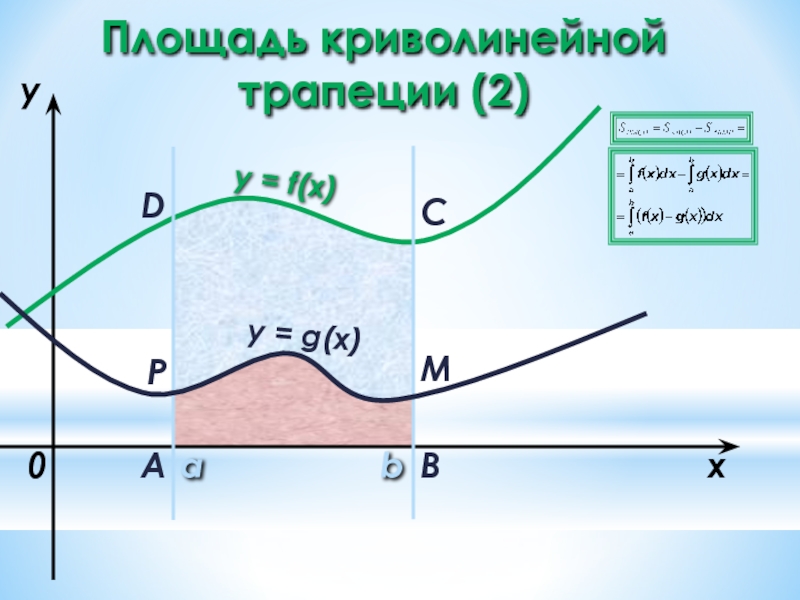
22. a b x
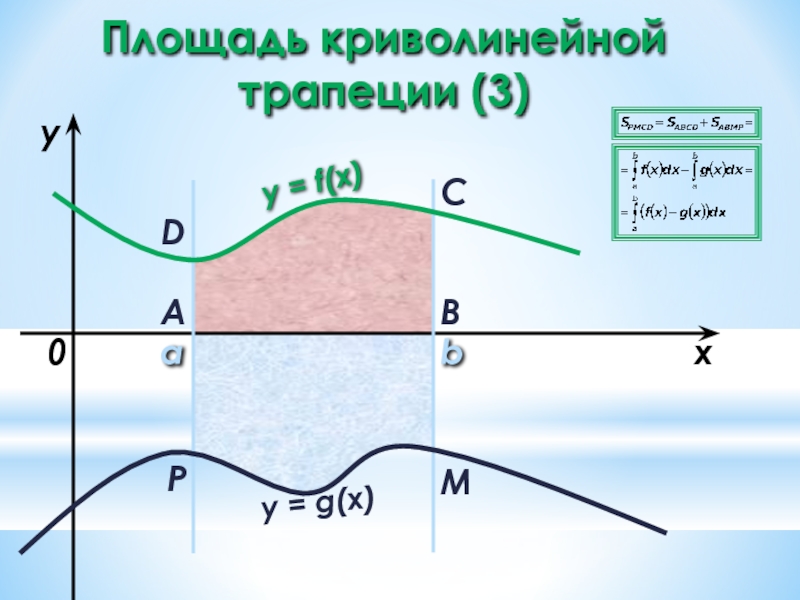
23. a b x y y
24. Пример 1: вычислить площадь
25. a b x y y
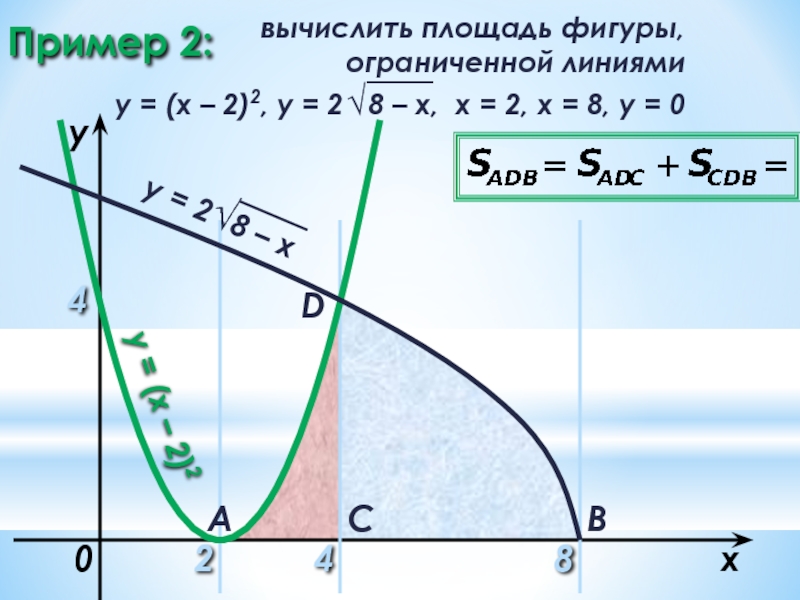
26. Пример 2: 2 8 x
27. Пример 2:

Слайд 1Первообразная и интеграл

Слайд 2Первообразная

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7Понятие первообразной
Функцию F(x) называют первообразной для функции f(x) на интервале (a;

b), если на нем производная функции F(x) равна f(x):

Операцию, обратную дифференцированию называют интегрированием.

Слайд 8

Слайд 9Примеры
f(x) = 2x; F(x) = x2
F′(x)=

(x2)′ = 2x = f(x)

f(x) = – sin x; F(x) = сos x
F′(x)= (cos x)′ = – sin x = f(x)

f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F′(x)= (2x3 + 4x)′ = 6x2 + 4 = f(x)

f(x) = 1/cos2 x; F(x) = tg x
F′(x)= (tg x)′ = 1/cos2 x= f(x)

Слайд 10Правила отыскания первообразных

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15Таблица первообразных
f(x)
F(x)
F(x)

Слайд 16Неопределенный интеграл
Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x)

называют любую ее первообразную функцию.

Где С – произвольная постоянная (const).

Слайд 17Примеры

Слайд 18Определенный интеграл
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что

определенный интеграл равен площади криволинейной трапеции, образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.

Слайд 19Вычисление определенного интеграла

Слайд 20
Площадь криволинейной трапеции

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y =

Слайд 21
Площадь криволинейной трапеции (1)

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y

= 0

Слайд 22

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P
Площадь криволинейной трапеции (2)

Слайд 23

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P

Площадь криволинейной трапеции (3)

Слайд 24

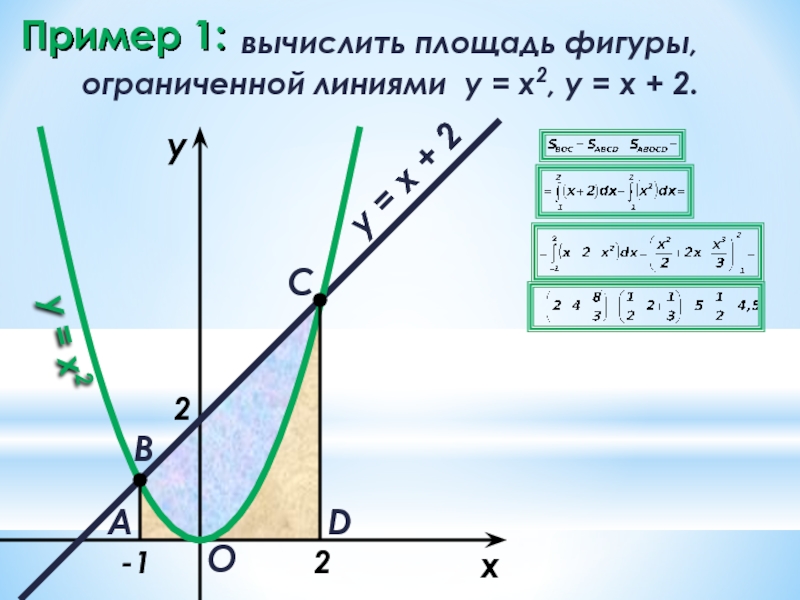
Пример 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y =

x + 2.

y = x2

y = x + 2

-1

Слайд 25

a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D

с
Е
Площадь криволинейной трапеции (4)

Слайд 26

Пример 2:
2
8
x
y = (x – 2)2
0
A
B
C
D
4
y

4

Слайд 27Пример 2:

Скачать презентацию

Первообразная и интеграл презентация

Содержание

Слайд 1Первообразная и интеграл

Слайд 2Первообразная

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7Понятие первообразной
Функцию F(x) называют первообразной для функции f(x) на интервале (a;

Слайд 8

Слайд 9Примеры
f(x) = 2x; F(x) = x2
F′(x)=

Слайд 10Правила отыскания первообразных

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15Таблица первообразных
f(x)
F(x)
F(x)

Слайд 16Неопределенный интеграл
Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x)

Слайд 17Примеры

Слайд 18Определенный интеграл
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что

Слайд 19Вычисление определенного интеграла

Слайд 20
Площадь криволинейной трапеции

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y =

Слайд 21
Площадь криволинейной трапеции (1)

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y

Слайд 22

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P
Площадь криволинейной трапеции (2)

Слайд 23

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P

Площадь криволинейной трапеции (3)

Слайд 24

Пример 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y =

Слайд 25

a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D

с
Е
Площадь криволинейной трапеции (4)

Слайд 26

Пример 2:
2
8
x
y = (x – 2)2
0
A
B
C
D
4
y

4

Слайд 27Пример 2:

Обратная связь

Что такое ThePresentation.ru?

Первообразная и интеграл презентация

Содержание

Слайд 1Первообразная и интеграл

Слайд 2Первообразная

Слайд 7Понятие первообразнойФункцию F(x) называют первообразной для функции f(x) на интервале (a;

Слайд 9Примерыf(x) = 2x; F(x) = x2 F′(x)=

Слайд 10Правила отыскания первообразных

Слайд 15Таблица первообразныхf(x)F(x)F(x)

Слайд 16Неопределенный интегралНеопределенным интегралом от непрерывной на интервале (a; b) функции f(x)

Слайд 17Примеры

Слайд 18Определенный интеграл– формула Ньютона-Лейбница.Геометрический смысл определенного интеграла заключается в том, что

Слайд 19Вычисление определенного интеграла

Слайд 20Площадь криволинейной трапеции abxyy = f(x)0ABCDx = ax = by =

Слайд 21Площадь криволинейной трапеции (1) abxyy = f(x)0ABCDx = ax = by

Слайд 22abxyy = f(x)0y = g(x)ABCDMPПлощадь криволинейной трапеции (2)

Слайд 23abxyy = f(x)0y = g(x)ABCDMPПлощадь криволинейной трапеции (3)

Слайд 24Пример 1:вычислить площадь фигуры, ограниченной линиями y = x2, y =

Слайд 25abxyy = f(x)0y = g(x)ABCDсЕПлощадь криволинейной трапеции (4)

Слайд 26Пример 2:28xy = (x – 2)20ABCD4y4

Слайд 27Пример 2:

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 7Понятие первообразной
Функцию F(x) называют первообразной для функции f(x) на интервале (a;

Слайд 9Примеры
f(x) = 2x; F(x) = x2
F′(x)=

Слайд 15Таблица первообразных
f(x)
F(x)
F(x)

Слайд 16Неопределенный интеграл
Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x)

Слайд 18Определенный интеграл
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что

Слайд 20
Площадь криволинейной трапеции

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y =

Слайд 21
Площадь криволинейной трапеции (1)

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y

Слайд 22

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P
Площадь криволинейной трапеции (2)

Слайд 23

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P

Площадь криволинейной трапеции (3)

Слайд 24

Пример 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y =

Слайд 25

a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D

с
Е
Площадь криволинейной трапеции (4)

Слайд 26

Пример 2:
2
8
x
y = (x – 2)2
0
A
B
C
D
4
y

4