- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Первичное описание исходных данных презентация
Содержание
- 1. Первичное описание исходных данных
- 2. Результаты психологических исследований обычно фиксируются в
- 3. Метрические данные можно представить в виде
- 4. Сводный протокол Первый шаг на пути статистической
- 6. Вариационный ряд В таблице колонка, в которую
- 7. Если же варианты расположить в виде
- 8. Упорядоченный ряд распределения, в котором указана
- 9. ПОСТРОЕНИЕ ВАРИАЦИОННЫХ РЯДОВ Известно два вида
- 10. Алгоритм построения интервальных вариационных рядов Определяем число
- 12. 2. Определяем разность между максимальным
- 13. 3. Определяем ширину классового интервала
- 14. 4. Находим нижнюю границу первого
- 15. 5.Находим верхнюю границу первого класса
- 17. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ВАРИАЦИОННЫХ РЯДОВ Чтобы
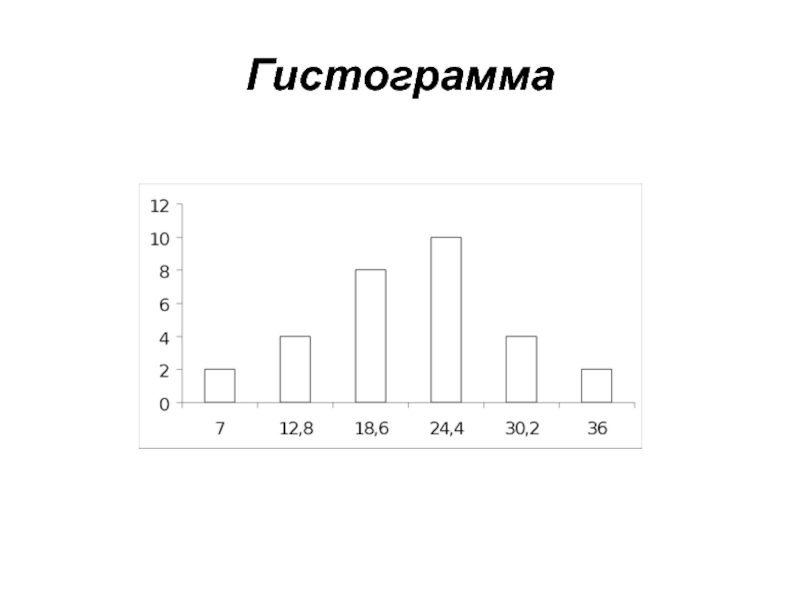
- 18. Гистограмма
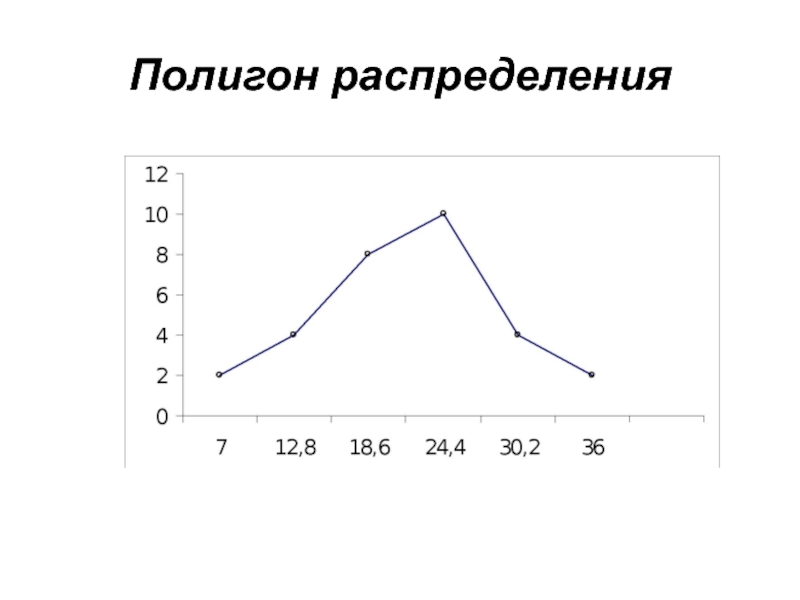
- 19. Полигон распределения
- 20. Спасибо за внимание!
Слайд 2
Результаты психологических исследований обычно фиксируются в протоколах. Собранный материал затем подвергается
статистической обработке.
Цель обработки - извлечение из массы данных объективных и убедительных выводов, подтверждающих или отвергающих гипотезу исследователя, выдвинутую на этапе планирования исследования.
Цель обработки - извлечение из массы данных объективных и убедительных выводов, подтверждающих или отвергающих гипотезу исследователя, выдвинутую на этапе планирования исследования.
Слайд 3
Метрические данные можно представить в виде ряда значений, называемого статистической совокупностью
(массивом).
Каждый член этой совокупности, в свою очередь, называется вариантой.
Каждый член этой совокупности, в свою очередь, называется вариантой.
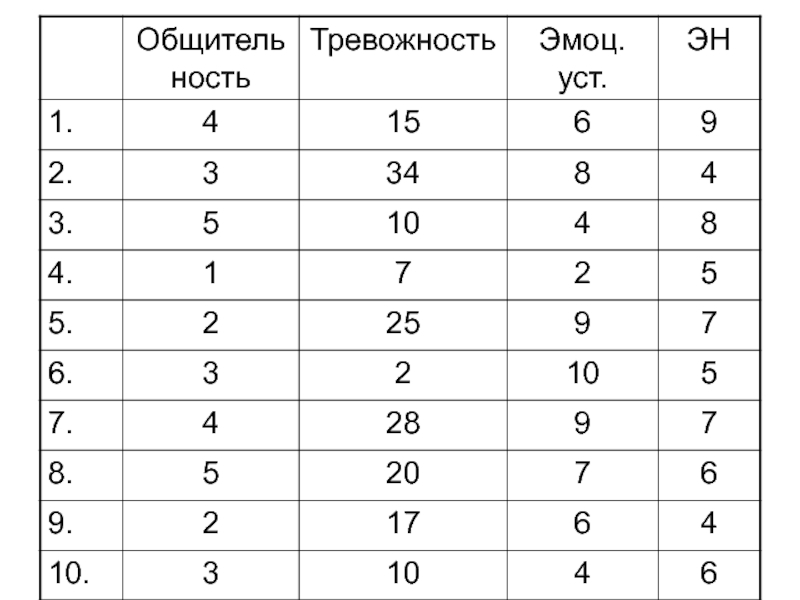
Слайд 4Сводный протокол
Первый шаг на пути статистической обработки данных заключается в группировке
полученных результатов и их представление в виде сводных таблиц ( сводных протоколов):
Слайд 6Вариационный ряд
В таблице колонка, в которую занесены значения первого показателя для
10 испытуемых, представляет из себя некоторый числовой ряд: 4 3 5 1 2 3 4 5 2 3. Расположим эту совокупность в порядке возрастания величины признака: 1 2 2 3 3 3 4 5 5. Получился ранжированный ряд. Видно, что наш признак варьирует в пределах от 1 до 5.
Слайд 7
Если же варианты расположить в виде двойного ряда, учитывая их повторяемость
в исходном ряду, совокупность данных будет выглядеть следующим образом:
варианты (х): 1 2 3 4 5
повторяемость вариант (p): 1 2 3 2 2
варианты (х): 1 2 3 4 5
повторяемость вариант (p): 1 2 3 2 2
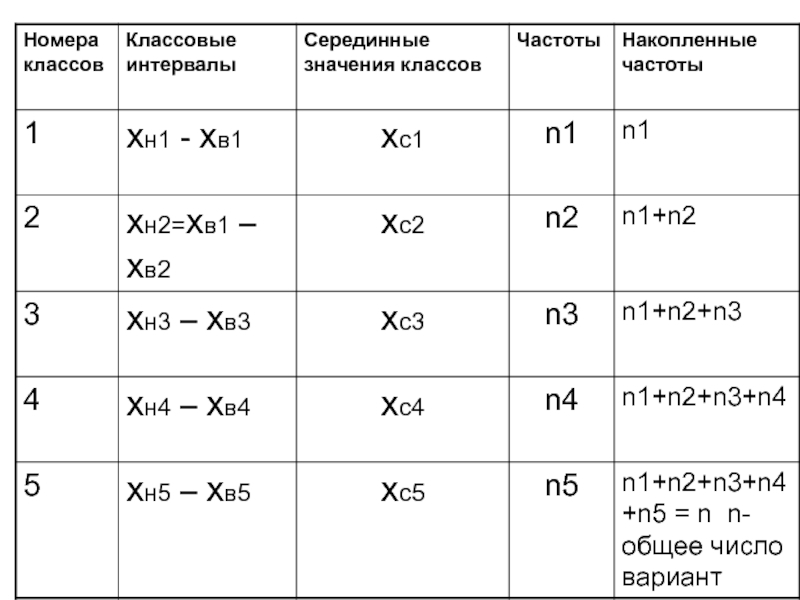
Слайд 8
Упорядоченный ряд распределения, в котором указана повторяемость вариант, принадлежащих к данной
совокупности, называется вариационным рядом. Числа, которые характеризуют встречаемость отдельных вариант в исходной совокупности, называют весами или частотами.
Слайд 9ПОСТРОЕНИЕ ВАРИАЦИОННЫХ РЯДОВ
Известно два вида вариационных рядов: безинтервальные и интервальные.
Безинтервальный вариационный ряд был уже рассмотрен ранее на примере, взятом из таблицы.
Когда совокупность достаточно большая, безинтервальный вариационный ряд плохо отражает закономерности варьирования признаков. В таких случаях целесообразнее построить интервальный вариационный ряд.
Когда совокупность достаточно большая, безинтервальный вариационный ряд плохо отражает закономерности варьирования признаков. В таких случаях целесообразнее построить интервальный вариационный ряд.
Слайд 10Алгоритм построения интервальных вариационных рядов
Определяем число классов по формуле К =
1+3,32 lg n (по Стерджесу) или К = 5 lg n (по Бруксу и Краузерсу).
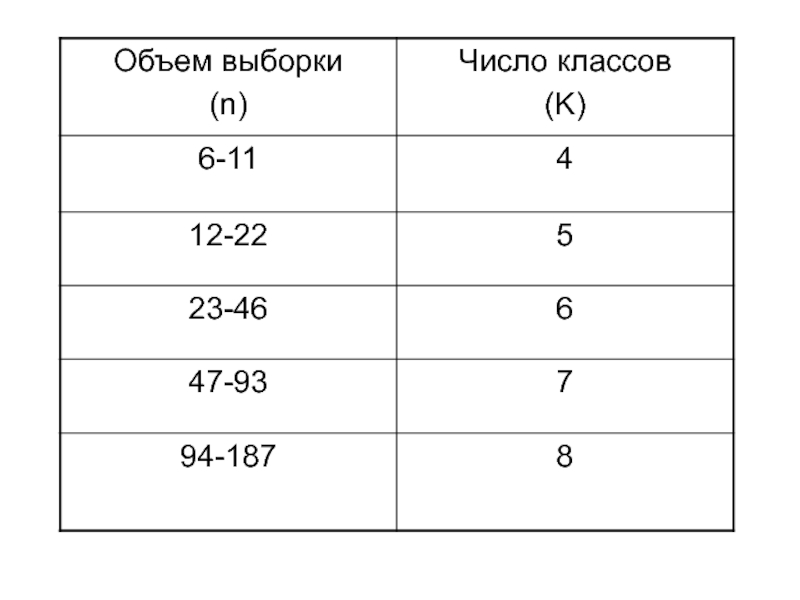
Число классов можно также определить по таблице (по Н.А. Плохинскому):
Число классов можно также определить по таблице (по Н.А. Плохинскому):
Слайд 12
2. Определяем разность между максимальным и минимальным значением вариант ряда
R, называемый вариационным размахом.
R = xmax - xmin
R = xmax - xmin
Слайд 15
5.Находим верхнюю границу первого класса по формуле
xв = xmin + 0,5 i
Начальные и конечные значения всех последующих классов можно вычислить путем последовательного прибавления величины классового интервала, начиная от первого.
Начальные и конечные значения всех последующих классов можно вычислить путем последовательного прибавления величины классового интервала, начиная от первого.
Слайд 17 ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ВАРИАЦИОННЫХ РЯДОВ
Чтобы придать большую наглядность закономерности варьирования
признаков, вариационные ряды принято изображать графически в виде гистограммы, или полигона.