- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Періодичність функцій. Властивості та графіки тригонометричних функцій. Розв’язування вправ презентация
Содержание
- 1. Періодичність функцій. Властивості та графіки тригонометричних функцій. Розв’язування вправ
- 2. Математичний диктант 1.Обчислити: cos210°. 2. Знайти значення виразу
- 3. .4.Обчисліть: . 5.Спростити вираз 6. Знайти
- 4. Періодичність функції Функція у = f(x) називається
- 5. Якщо функція у = f(x) періодична і
- 6. Виконання вправ 1. Обчисліть: a) sin 1470°;
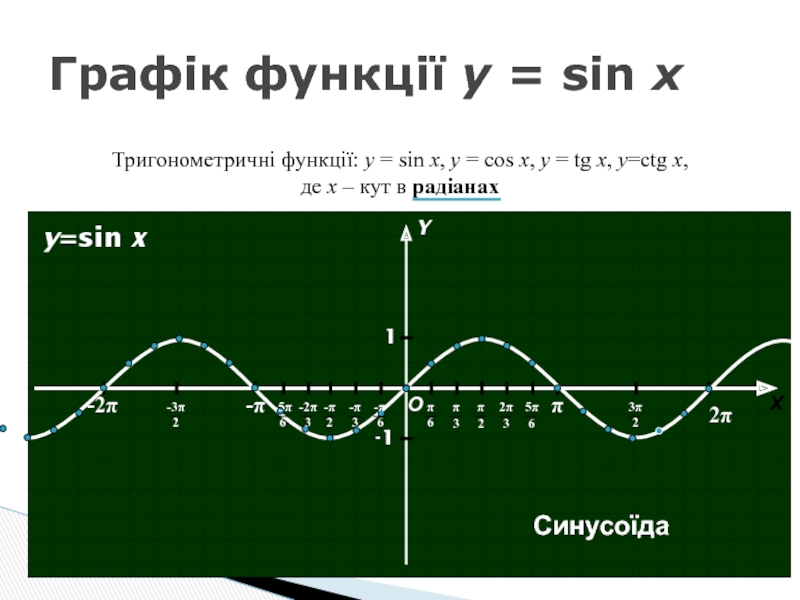
- 7. Графік функції y = sin x Тригонометричні
- 8. Функція y = sin x Властивості
- 9. 4. sin x = O при
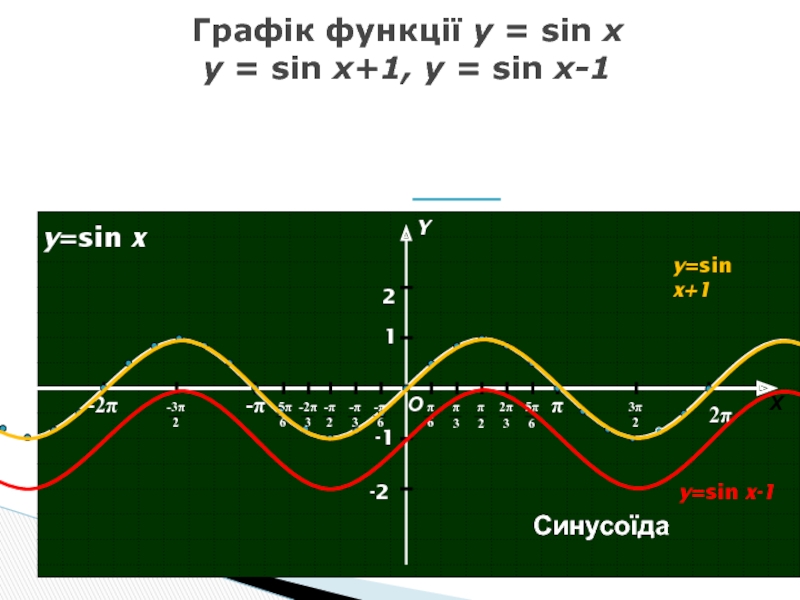
- 10. Графік функції y = sin x y
- 11. Графік функції y = sin x y
- 12. Графік функції y = 2sin x+1,
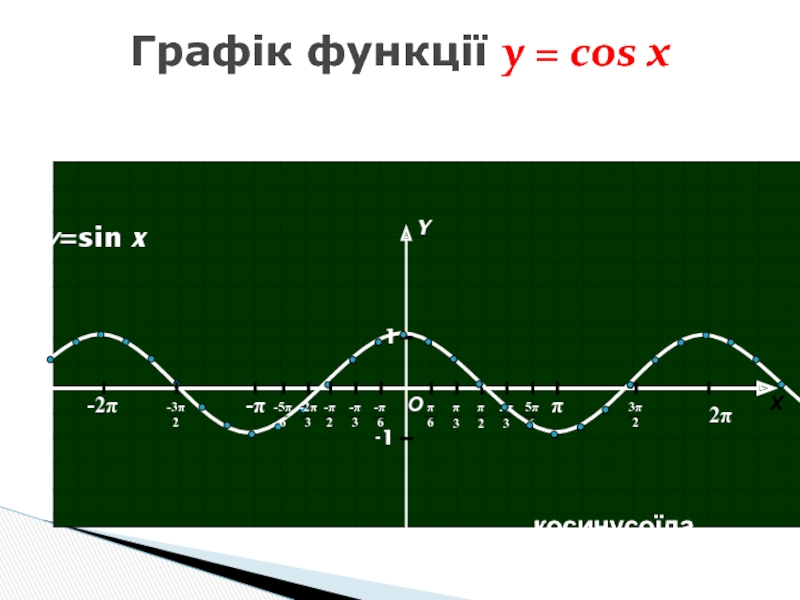
- 13. Графік функції y = cos x
- 14. Функція y = cos x Властивості
- 15. Властивості функції: 4. cos x =
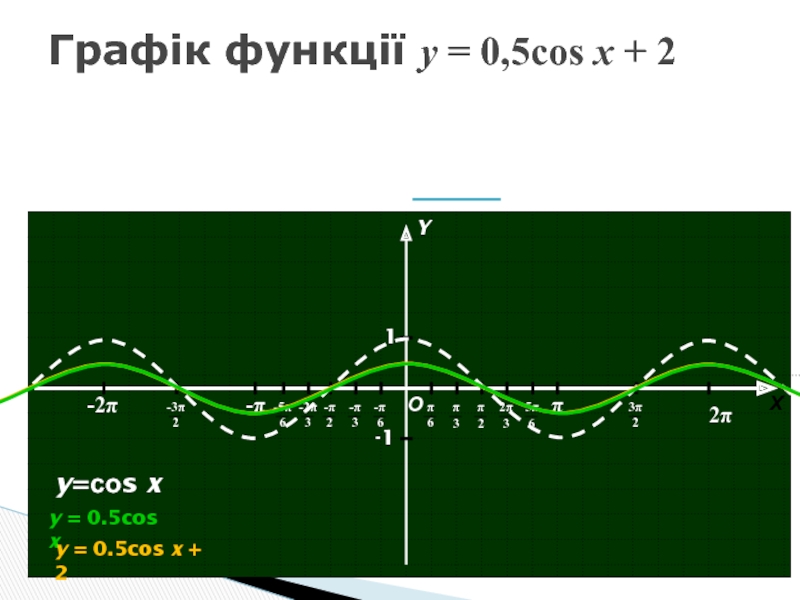
- 16. Графік функції y = 0,5cos x +
- 17. Властивості функції: D(ctg x) = x∈
- 18. 6. проміжки монотонності:
- 19. Властивості функції: D(ctg x) = x∈
- 20. 6. проміжки монотонності:
Слайд 4Періодичність функції
Функція у = f(x) називається періодичною з періодом Т 0,
sin(α + 2πn) = sin α
cos(α + 2πn) = cos α
2 π– періоди функцій синус і косинус
Слайд 5Якщо функція у = f(x) періодична і має період Т, то
Слайд 7Графік функції y = sin x
Тригонометричні функції: y = sin x,
О
Х
Y
1
-1
y=sin x
Синусоїда
Слайд 8Функція y = sin x
Властивості функції:
D(sin x) = R; Е(sin
y = sin x – непарна функція, графік симетричний відносно початку
координат
3. періодичність: T = 2π
Слайд 94. sin x = O при х = πn, n∈Z
5. проміжки знакосталості:
sin x > 0 при 0 + 2πn < x < π+ 2πn, n∈Z
sin x < 0 при π + 2πn < x < 2π+ 2πn, n∈Z
6. проміжки монотонності:
x∈ [- π /2 + 2πn; π /2 + 2πn], n∈Z – зростає
x∈ [ π /2 + 2πn; 3π /2 + 2πn], n∈Z– спадає
7. екстремуми:
y max = 1 при х = π /2 + 2πn, n∈Z
y min = - 1 при х = - π /2 + 2πn, n∈Z
9. похідна: (sin x )´ = cos x
Слайд 10Графік функції y = sin x y = sin x+1, y =
О
Х
Y
1
-1
y=sin x
Синусоїда
y=sin x+1
y=sin x-1
2
-2
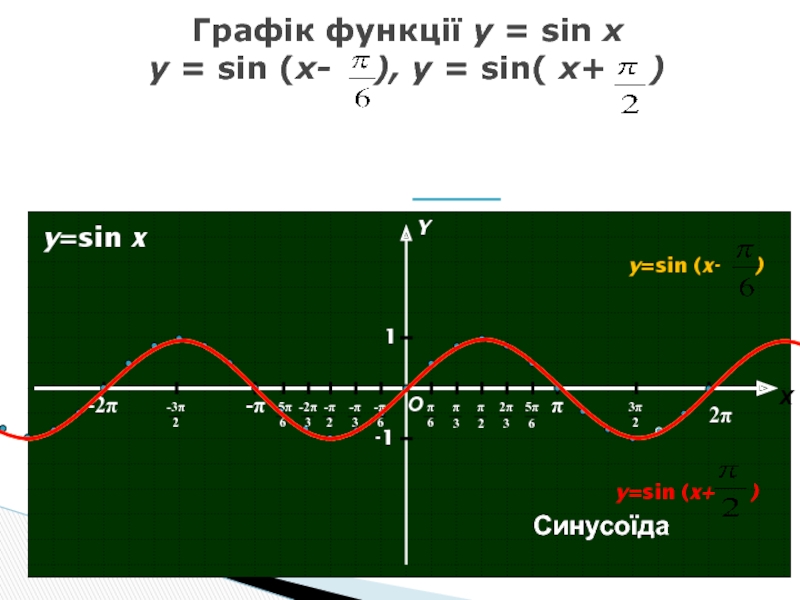
Слайд 11Графік функції y = sin x y = sin (x- ),
О
Х
Y
1
-1
y=sin x
Синусоїда
y=sin (x- )
y=sin (x+ )
Слайд 12Графік функції y = 2sin x+1, y = sin x, y =
О
Х
Y
1
-1
y=sin x
Синусоїда
y=2sin x
y=sin x+1
2
-2
Слайд 14Функція y = cos x
Властивості функції:
D(cos x) = R; Е(sin
y = cos x –парна функція,
графік симетричний відносно
осі ординат
3. періодичність: T = 2π
Слайд 15Властивості функції:
4. cos x = 0 при х = π
5. проміжки знакосталості
cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, n∈Z
cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, n∈Z
6. проміжки монотонності:
x∈ [ π+ 2πn; 2π+ 2πn], n∈Z –зростає
x∈ [0 + 2πn; π+ 2πn], n∈Z– спадає
7. екстремуми:
y max = 1 при х = 2πn, n∈Z
y min = - 1 при х = π+ 2πn, n∈Z
8. похідна: (cos x )´ = - sin x
Слайд 17Властивості функції:
D(ctg x) = x∈ R / πn, n∈Z
y
графік симетричний відносно початку
координат
Функція y = tg x
3. періодичніть: T = π
4. tg x = 0 при х = πn, n∈Z (нулі функції)
5. проміжки знакосталості:
tg x > 0 при 0 + πn < x < π /2 + πn, n∈Z
tg x < 0 при - π /2 + πn < x < 0 + πn, n∈Z
Слайд 186. проміжки монотонності:
x∈ [- π /2
экстремумів немає
E(tg x) = R
9. похідна: (tg x )´ = 1/cos 2 x
Слайд 19Властивості функції:
D(ctg x) = x∈ R / πn, n∈Z
y
графік симетричний відносно початку
координат
Функція y = ctg
3. періодичність: T = π
4. ctg x = 0 при х = π /2 + πn, n∈Z (нулі функції)
5. проміжки знакосталості:
ctg x > 0 при 0 + πn < x < π /2 + πn, n∈Z
ctg x < 0 при π /2 + πn < x < π + πn, n∈Z
Слайд 206. проміжки монотонності:
x∈ [0+ πn; π+
екстремумів немає
E(ctg x) = R
9. похідна: (ctg x )´ = - 1/sin 2 x






![Функція y = sin xВластивості функції:D(sin x) = R; Е(sin x)є[-1;1]y = sin x –](/img/tmb/5/476547/cb0c2bd4583a4d513515979a49c6e50e-800x.jpg)


![Функція y = cos xВластивості функції:D(cos x) = R; Е(sin x)є[-1;1].y = cos x –парна](/img/tmb/5/476547/96a3a8ed1c2d5acfc54cef39f12ba9cc-800x.jpg)


![6. проміжки монотонності: x∈ [- π /2 + πn; π /2 + πn], n∈Z](/img/tmb/5/476547/d39205e8a9510710a23184b20190adca-800x.jpg)

![6. проміжки монотонності: x∈ [0+ πn; π+ πn], n∈Z – спадаєекстремумів немаєE(ctg x) =](/img/tmb/5/476547/55065fb4937dc52cc89cdda9bdcb369f-800x.jpg)