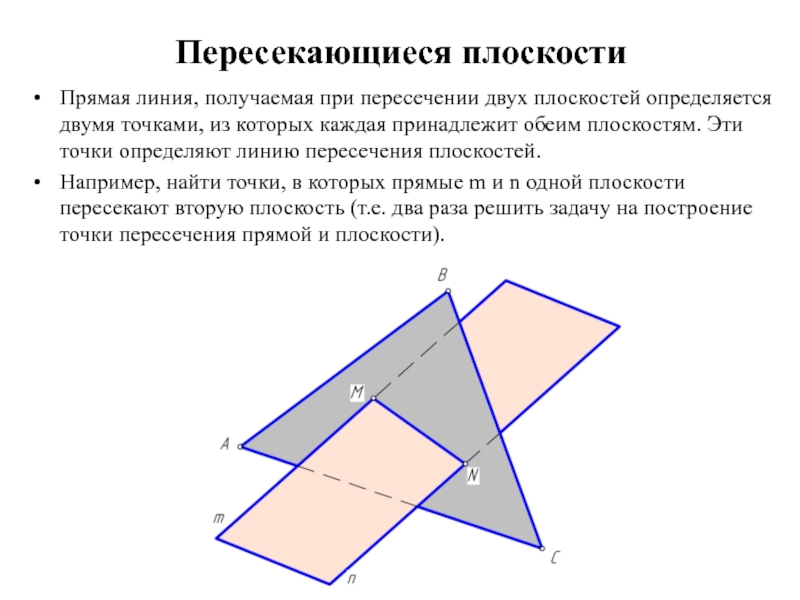
из которых каждая принадлежит обеим плоскостям. Эти точки определяют линию пересечения плоскостей.
Например, найти точки, в которых прямые m и n одной плоскости пересекают вторую плоскость (т.е. два раза решить задачу на построение точки пересечения прямой и плоскости).
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пересекающиеся плоскости презентация
Содержание
- 1. Пересекающиеся плоскости
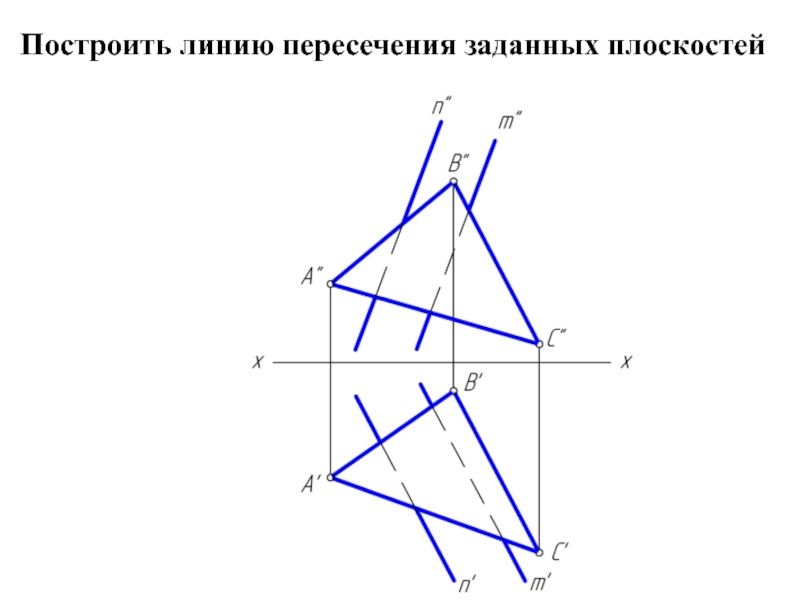
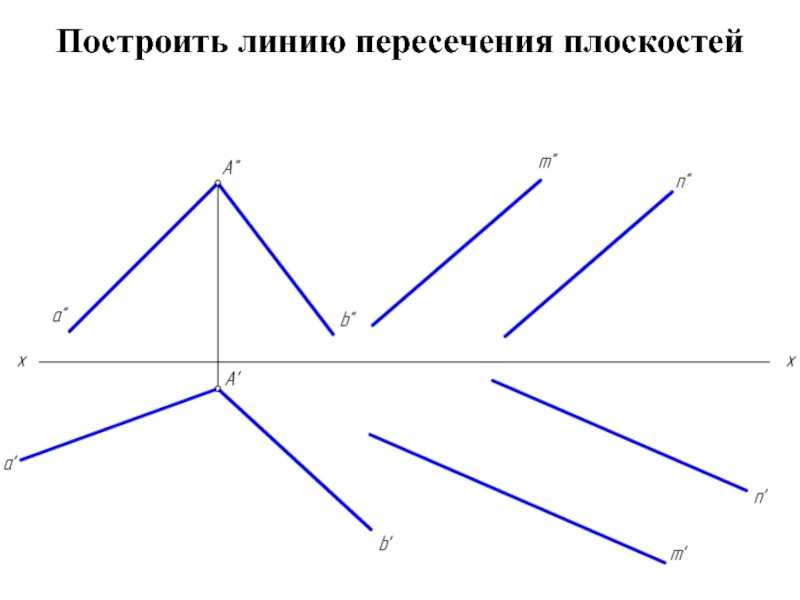
- 2. Построить линию пересечения заданных плоскостей
- 7. Общий случай построения линии пересечения плоскостей Одна
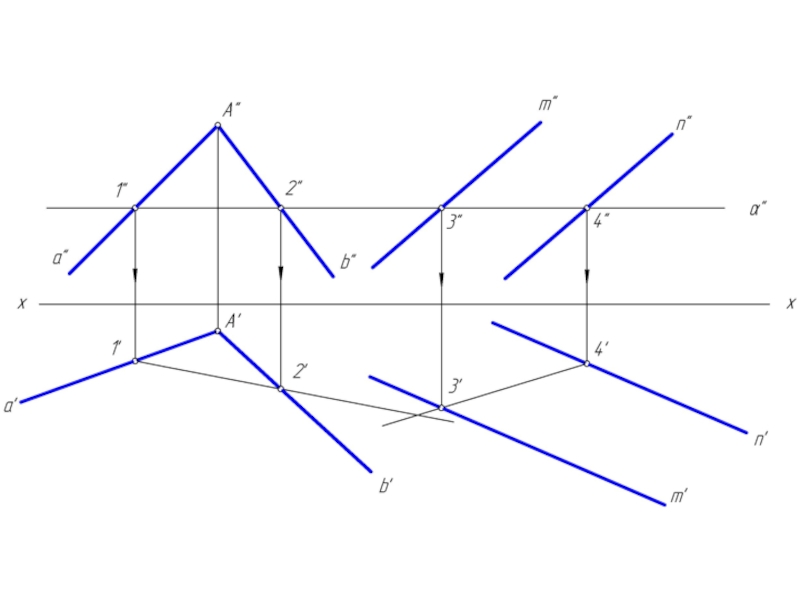
- 8. Построить линию пересечения плоскостей
- 13. Взаимно перпендикулярные прямая и плоскость Прямая перпендикулярна
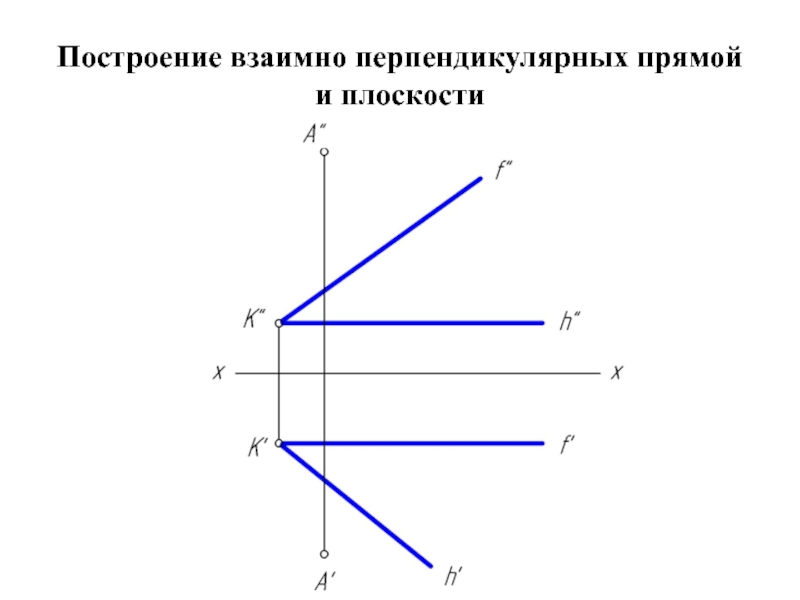
- 14. Построение взаимно перпендикулярных прямой и плоскости
- 17. Взаимно перпендикулярные плоскости Две плоскости взаимно перпендикулярны,
- 18. Так как через прямую m можно
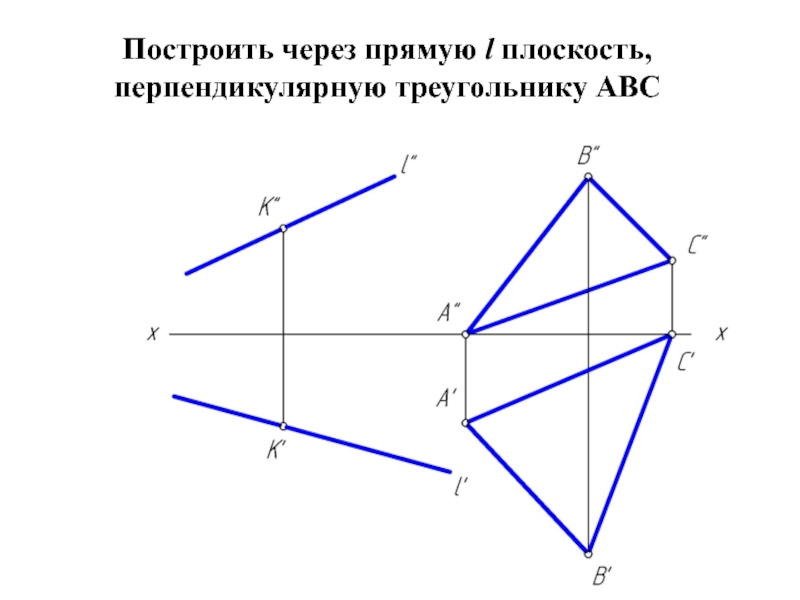
- 19. Построить через прямую l плоскость, перпендикулярную треугольнику АВС
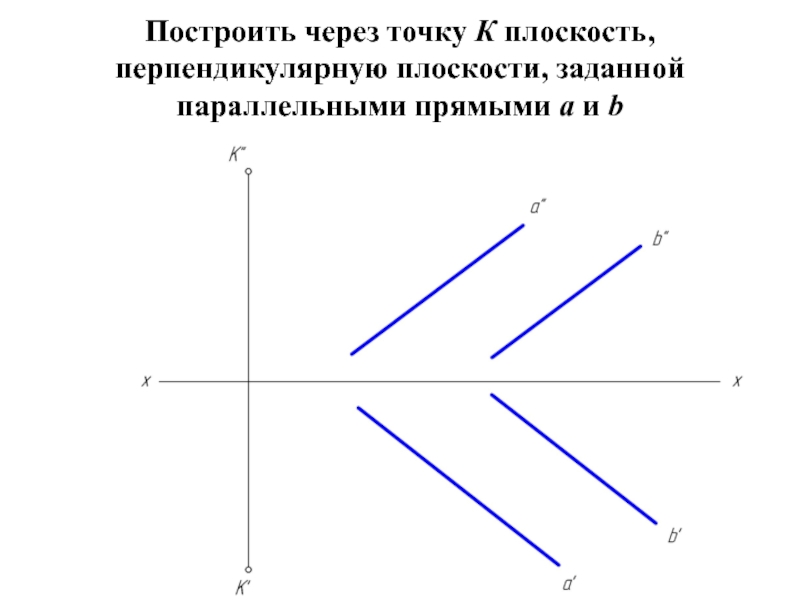
- 23. Построить через точку К плоскость, перпендикулярную плоскости, заданной параллельными прямыми a и b
- 26. Взаимно перпендикулярные прямые общего положения Задача: Через
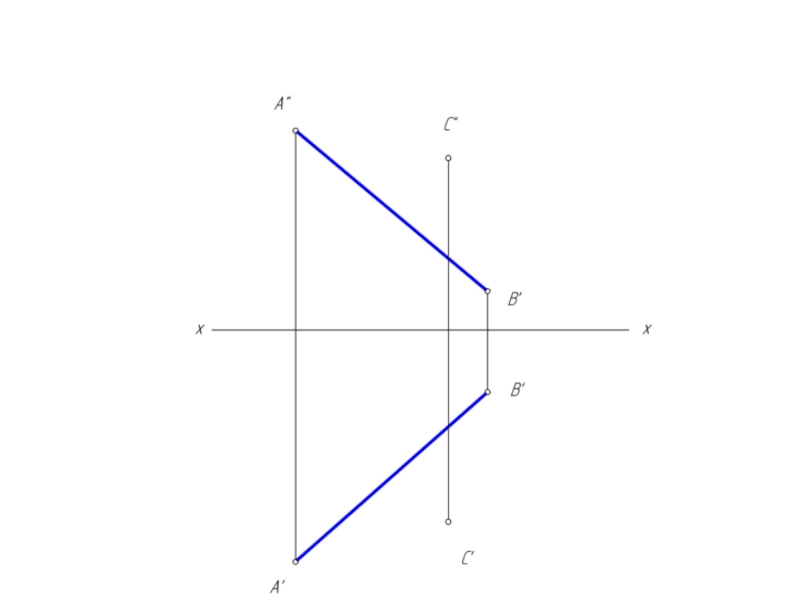
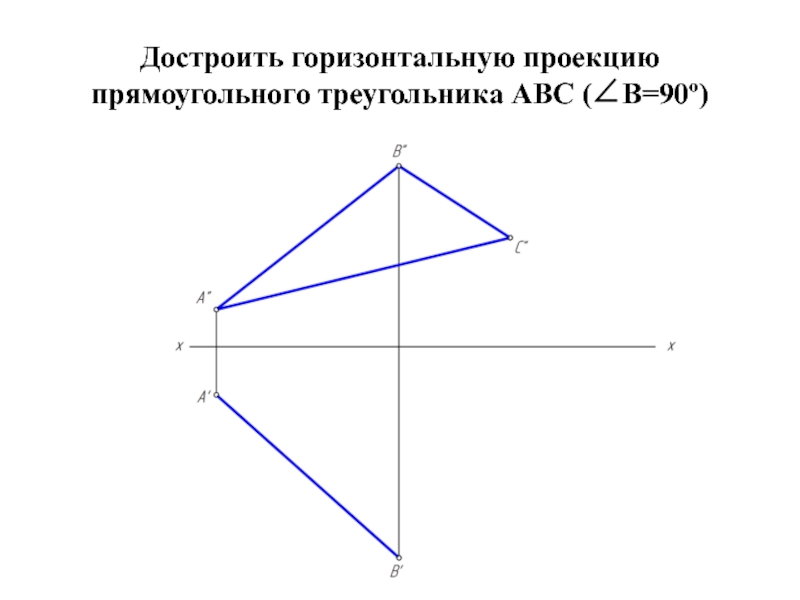
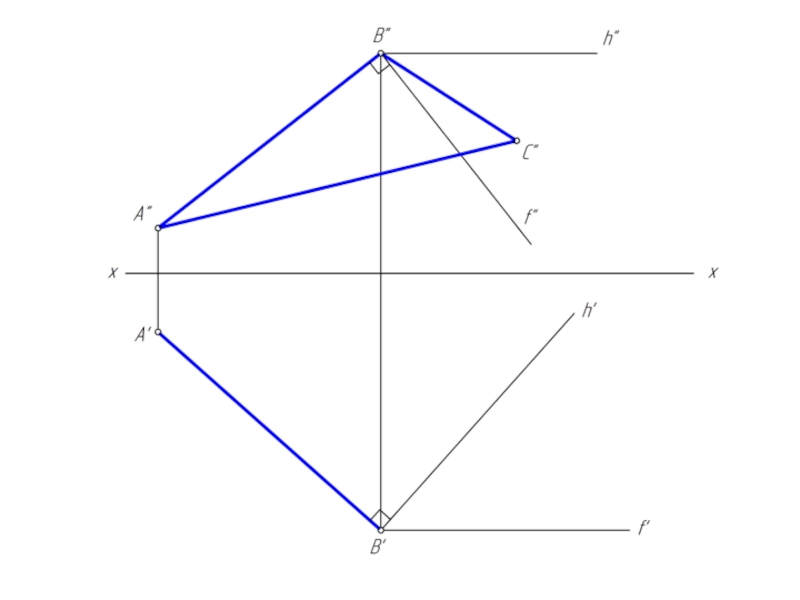
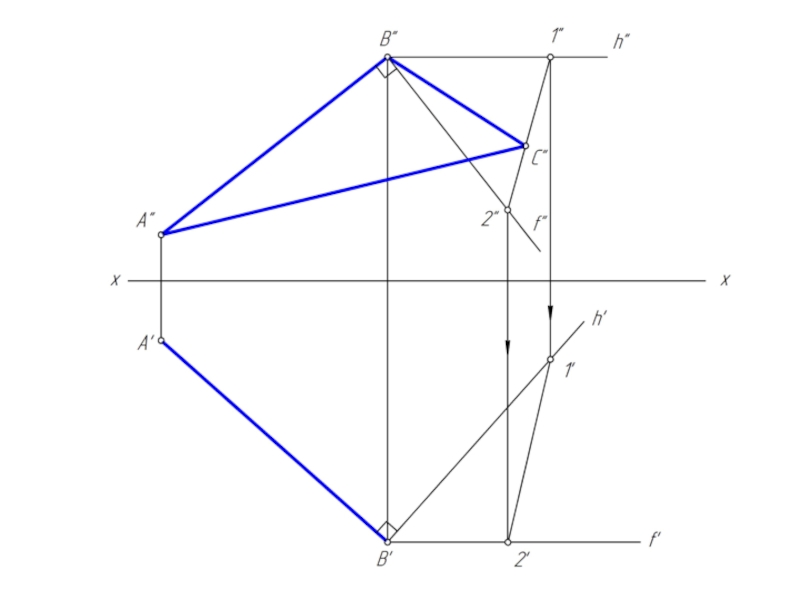
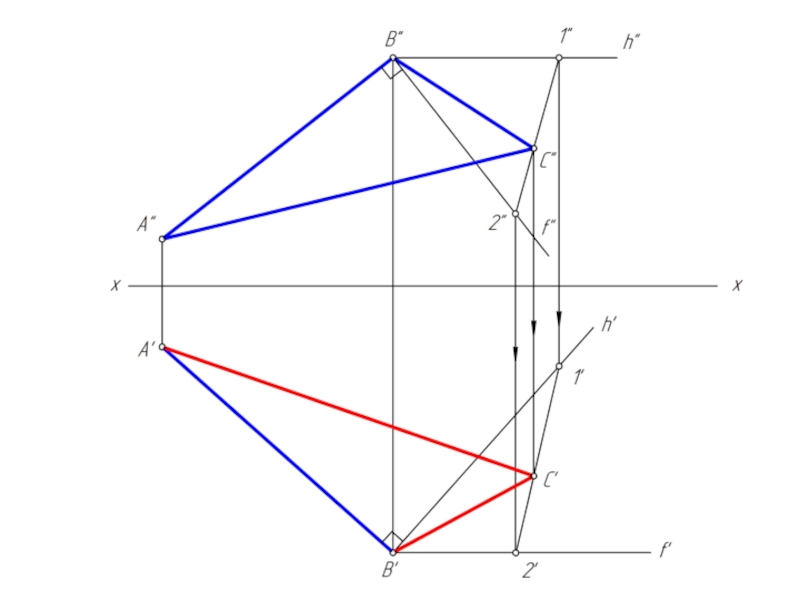
- 32. Достроить горизонтальную проекцию прямоугольного треугольника АВС (∠В=90º)
Слайд 1Пересекающиеся плоскости
Прямая линия, получаемая при пересечении двух плоскостей определяется двумя точками,
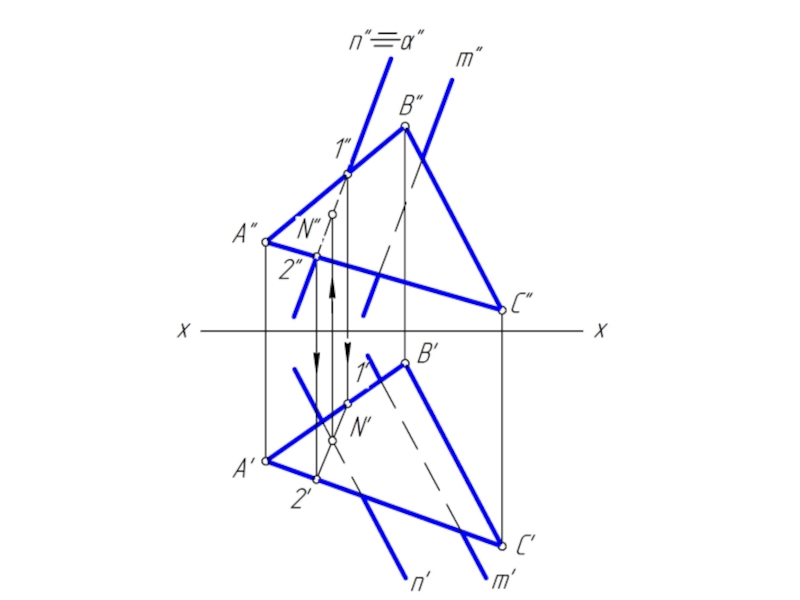
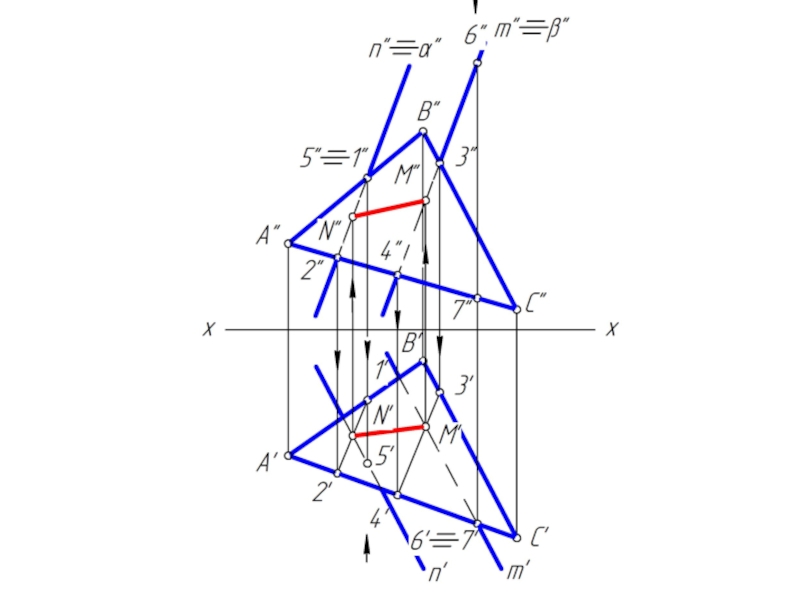
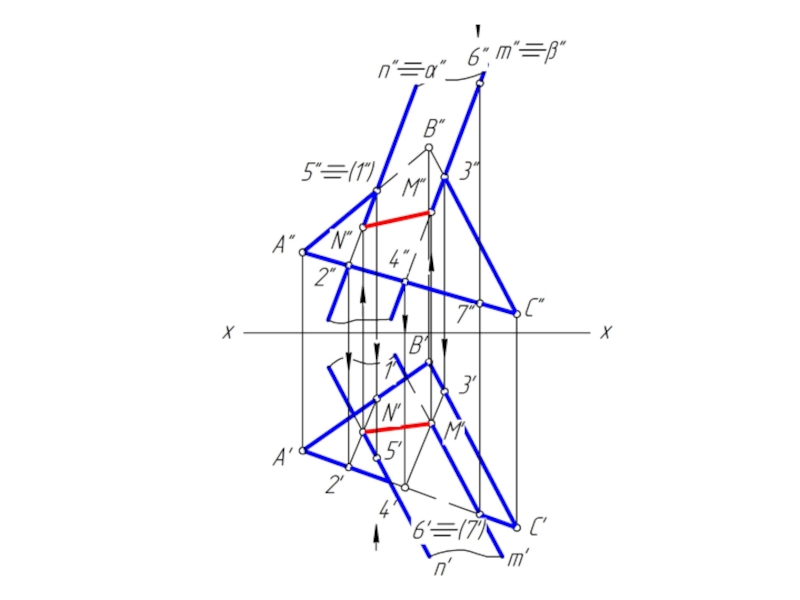
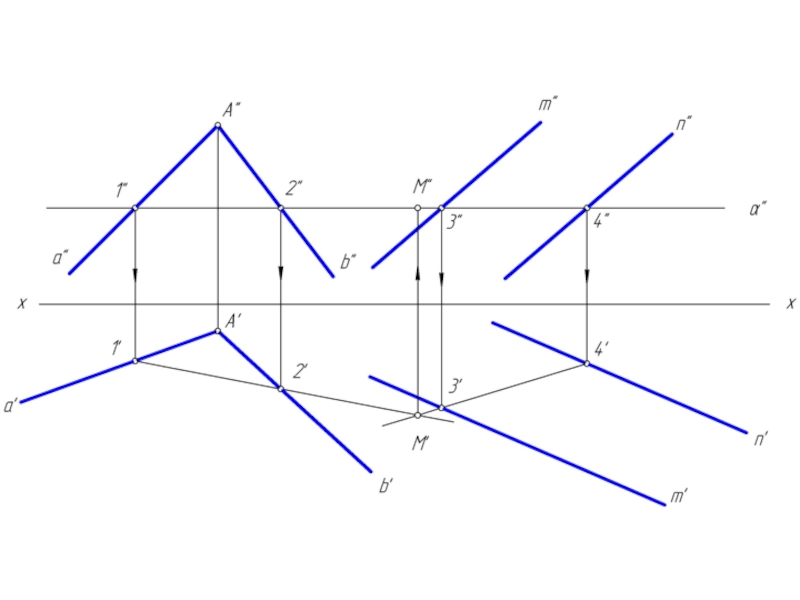
Слайд 7Общий случай построения линии пересечения плоскостей
Одна плоскость задана двумя пересекающимися прямыми
a и b, назовем ее φ;
Вторая плоскость задана двумя параллельными прямыми m и n, назовем ее λ.
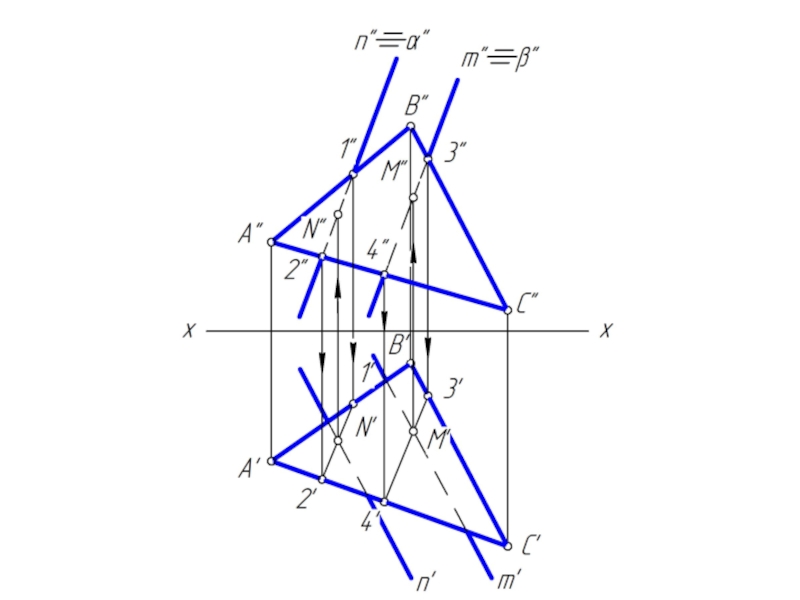
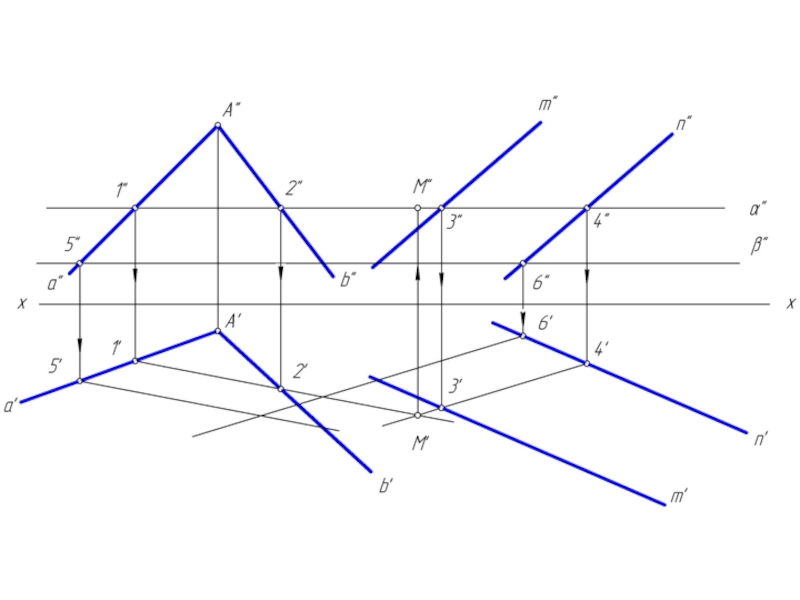
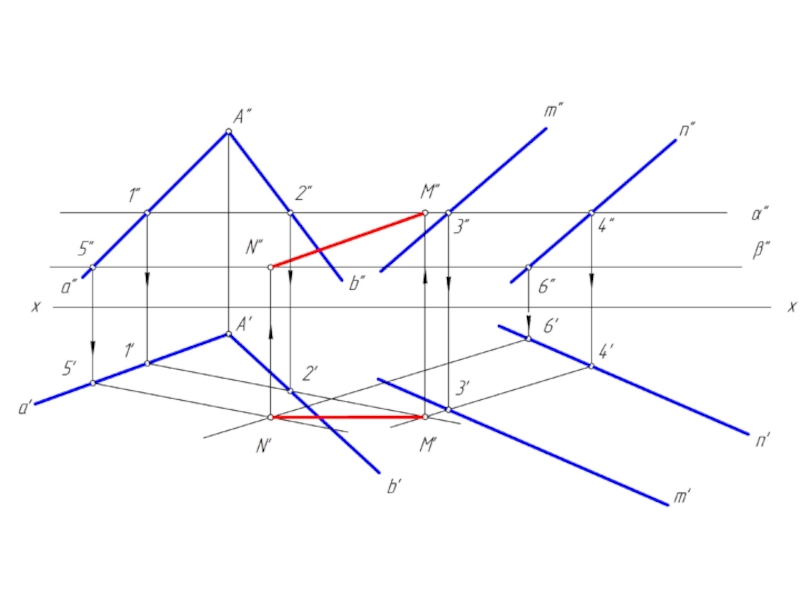
Чтобы найти две точки, принадлежащие одновременно двум заданным плоскостям φ и λ достаточно ввести две вспомогательные секущие плоскости α и β и выполнить последовательность операций:
(φ∩α) ∩ (λ∩α) = M; (φ∩β) ∩ (λ∩β) = N
Вспомогательным плоскостям α и β необходимо придать проецирующее положение, которое позволяет без дополнительных построений найти линию пересечения с заданными плоскостями φ и λ.
Вторая плоскость задана двумя параллельными прямыми m и n, назовем ее λ.
Чтобы найти две точки, принадлежащие одновременно двум заданным плоскостям φ и λ достаточно ввести две вспомогательные секущие плоскости α и β и выполнить последовательность операций:
(φ∩α) ∩ (λ∩α) = M; (φ∩β) ∩ (λ∩β) = N
Вспомогательным плоскостям α и β необходимо придать проецирующее положение, которое позволяет без дополнительных построений найти линию пересечения с заданными плоскостями φ и λ.
Слайд 13Взаимно перпендикулярные прямая и плоскость
Прямая перпендикулярна плоскости, если она перпендикулярна к
двум пересекающимся прямым, принадлежащим этой плоскости.
Если в плоскости взять не произвольные пересекающиеся прямые, а ее горизонталь и фронталь, то появляется возможность в этом случае воспользоваться теоремой о проецировании прямого угла.
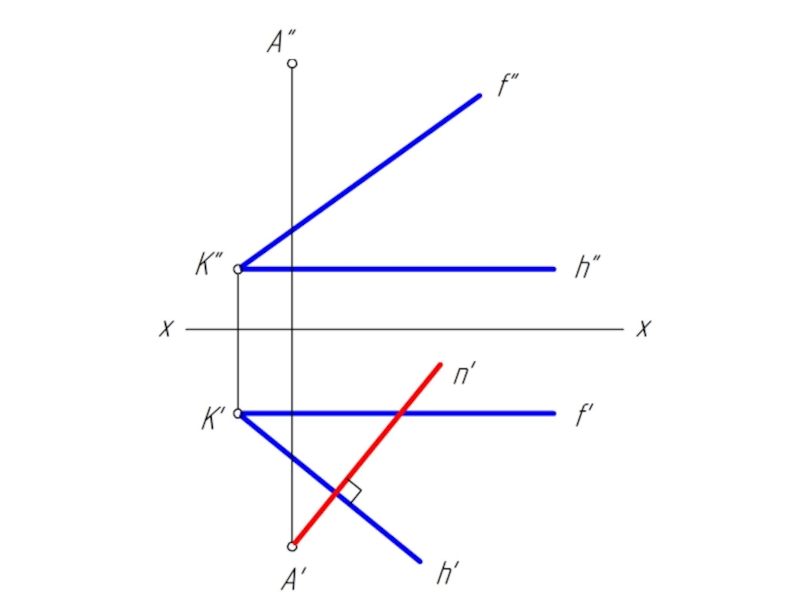
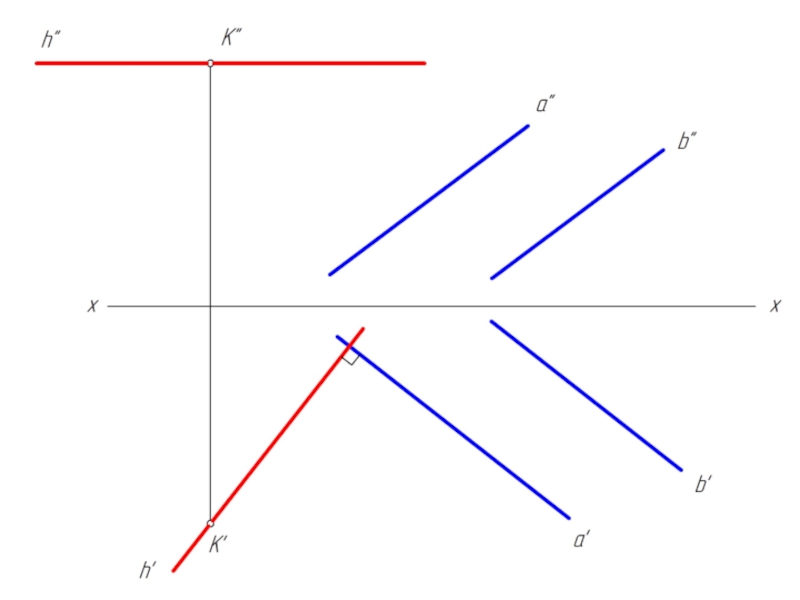
Для того чтобы прямая (n) в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой (n') была перпендикулярна горизонтальной проекции горизонтали плоскости (h'), а фронтальная проекция прямой (n'') была перпендикулярна фронтальной проекции фронтали (f'') этой плоскости.
n'⊥h' и n''⊥f ''
Если в плоскости взять не произвольные пересекающиеся прямые, а ее горизонталь и фронталь, то появляется возможность в этом случае воспользоваться теоремой о проецировании прямого угла.
Для того чтобы прямая (n) в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой (n') была перпендикулярна горизонтальной проекции горизонтали плоскости (h'), а фронтальная проекция прямой (n'') была перпендикулярна фронтальной проекции фронтали (f'') этой плоскости.
n'⊥h' и n''⊥f ''
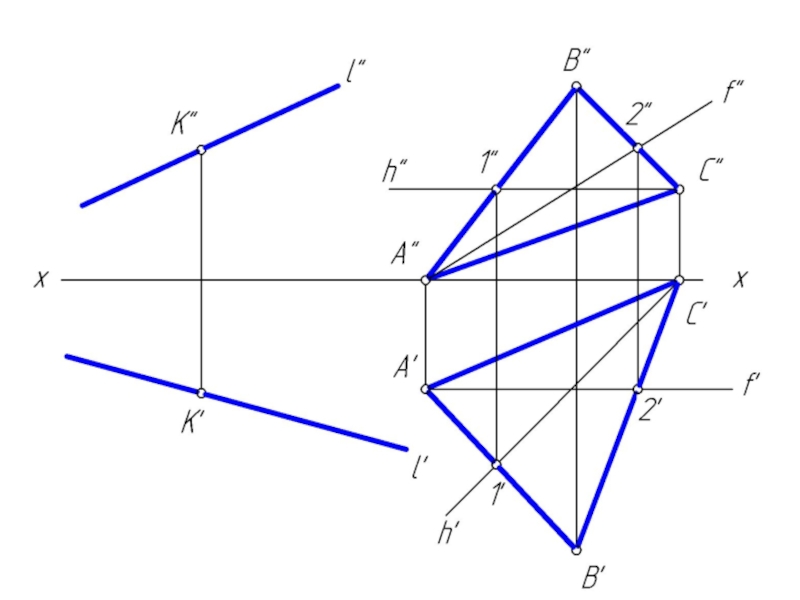
Слайд 17Взаимно перпендикулярные плоскости
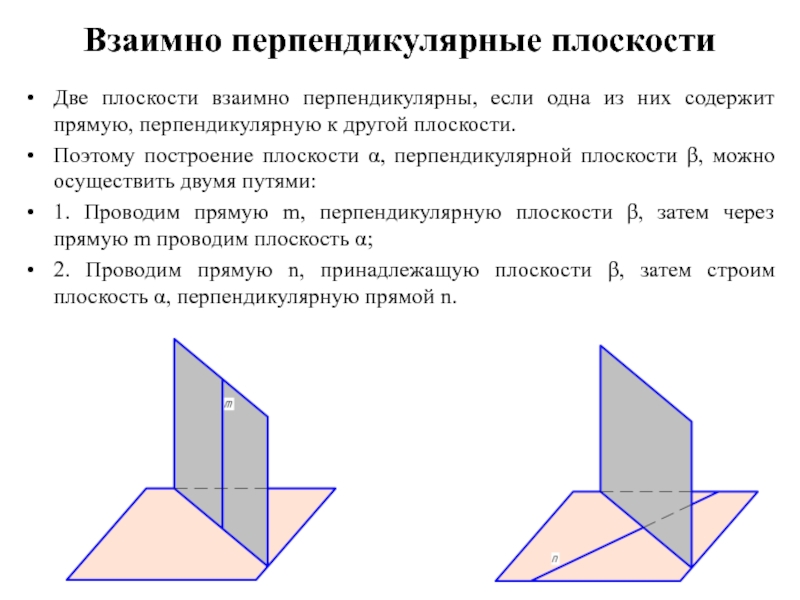
Две плоскости взаимно перпендикулярны, если одна из них содержит
прямую, перпендикулярную к другой плоскости.
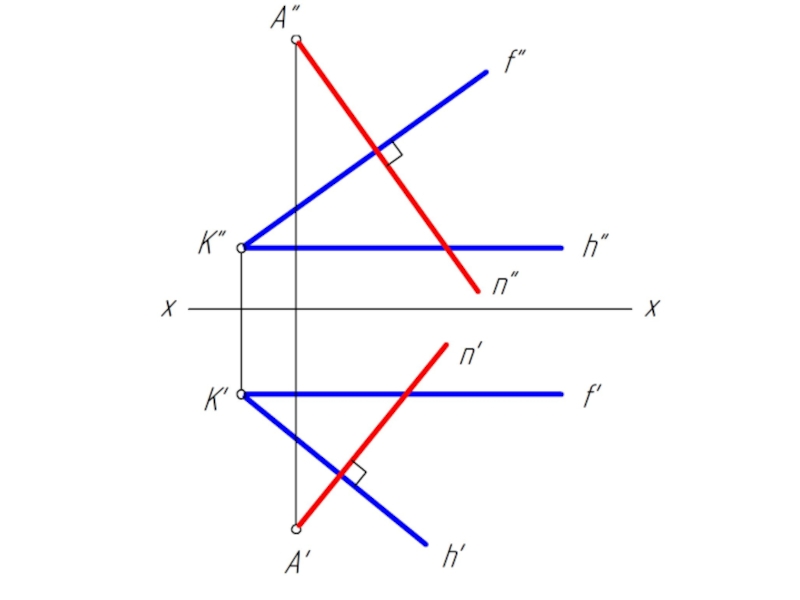
Поэтому построение плоскости α, перпендикулярной плоскости β, можно осуществить двумя путями:
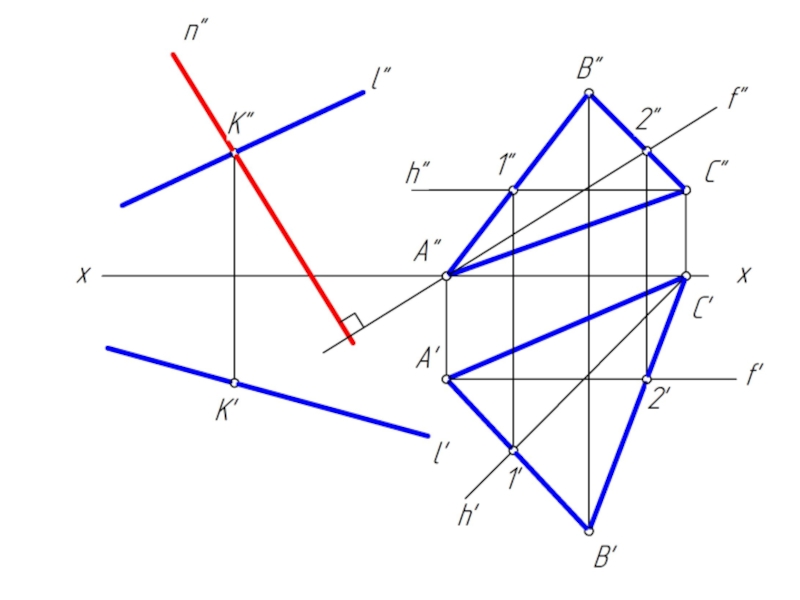
1. Проводим прямую m, перпендикулярную плоскости β, затем через прямую m проводим плоскость α;
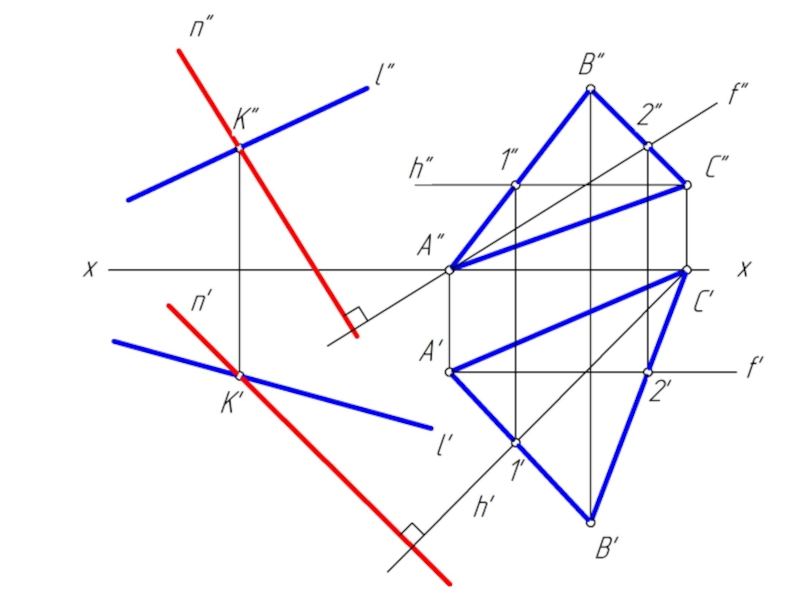
2. Проводим прямую n, принадлежащую плоскости β, затем строим плоскость α, перпендикулярную прямой n.
Поэтому построение плоскости α, перпендикулярной плоскости β, можно осуществить двумя путями:
1. Проводим прямую m, перпендикулярную плоскости β, затем через прямую m проводим плоскость α;
2. Проводим прямую n, принадлежащую плоскости β, затем строим плоскость α, перпендикулярную прямой n.
Слайд 18
Так как через прямую m можно провести множество плоскостей (первый путь
решения), то задача имеет множество решений.
То же самое происходит и при решении задачи по второму пути (в плоскости можно провести множество прямых n)
Чтобы конкретизировать задачу, необходимо указать дополнительные условия.
То же самое происходит и при решении задачи по второму пути (в плоскости можно провести множество прямых n)
Чтобы конкретизировать задачу, необходимо указать дополнительные условия.
Слайд 23Построить через точку К плоскость, перпендикулярную плоскости, заданной параллельными прямыми a
и b
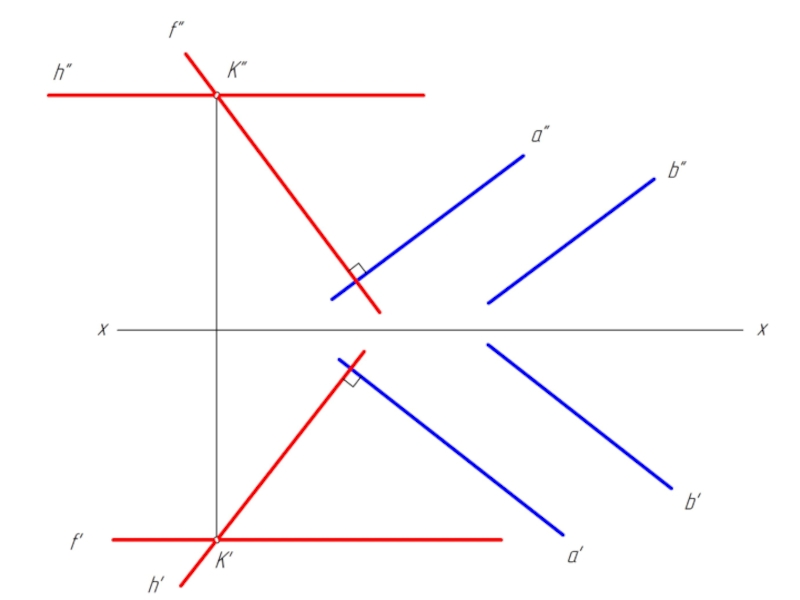
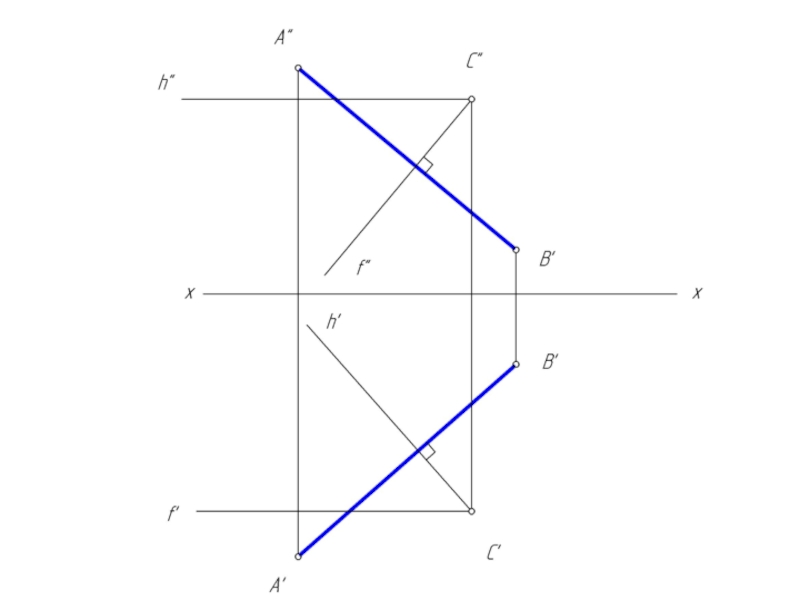
Слайд 26Взаимно перпендикулярные прямые общего положения
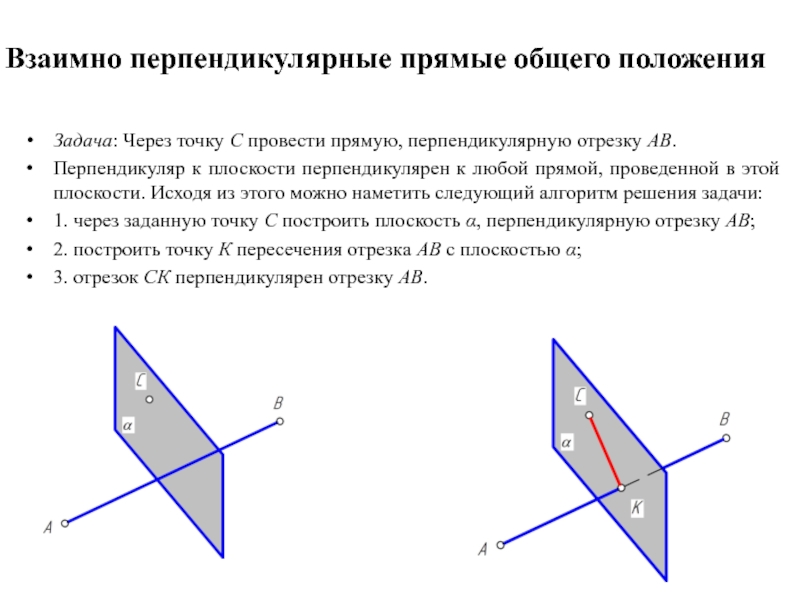
Задача: Через точку С провести прямую, перпендикулярную
отрезку АВ.
Перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости. Исходя из этого можно наметить следующий алгоритм решения задачи:
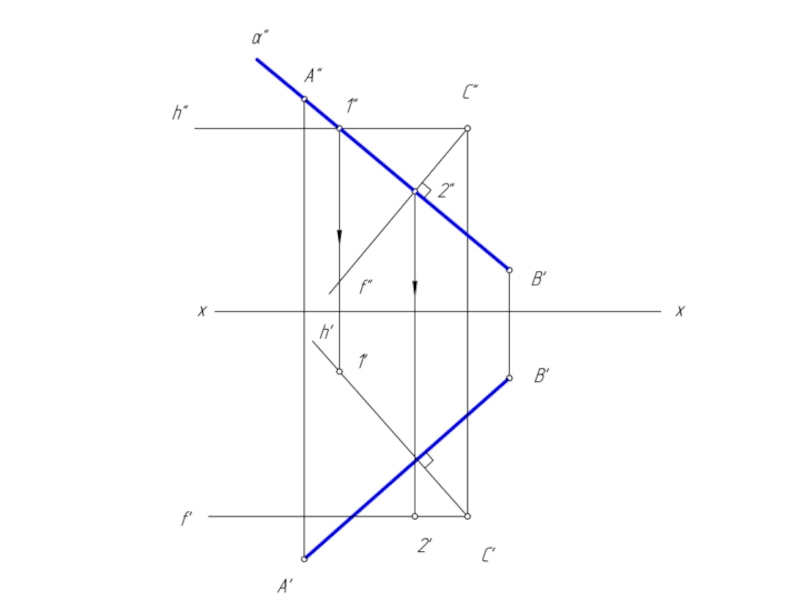
1. через заданную точку С построить плоскость α, перпендикулярную отрезку АВ;
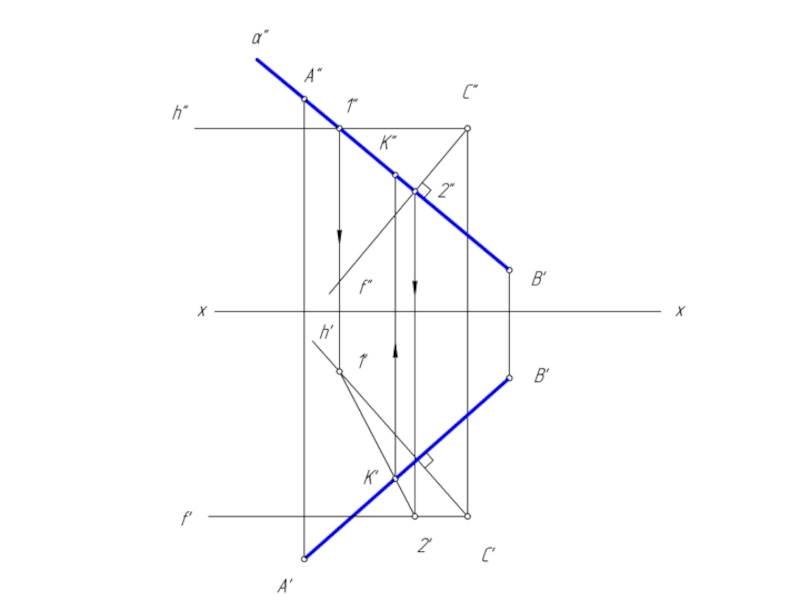
2. построить точку К пересечения отрезка АВ с плоскостью α;
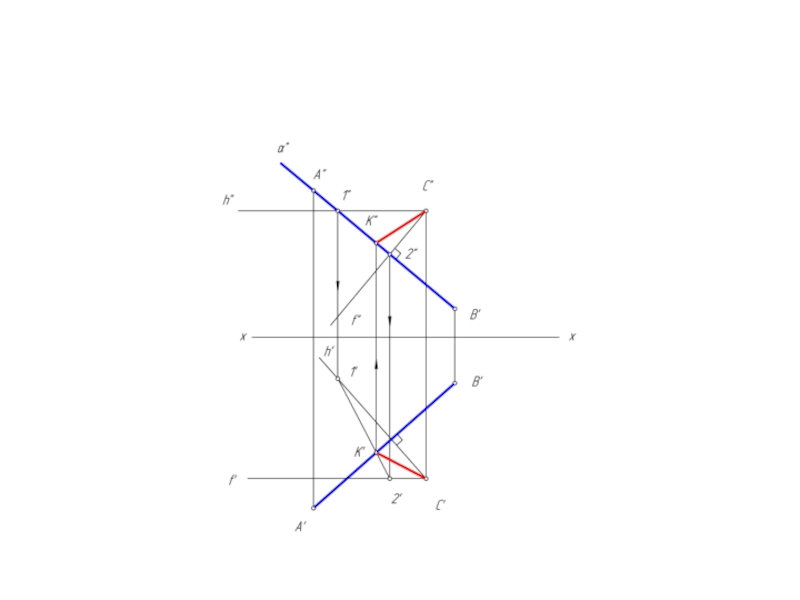
3. отрезок СК перпендикулярен отрезку АВ.
Перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости. Исходя из этого можно наметить следующий алгоритм решения задачи:
1. через заданную точку С построить плоскость α, перпендикулярную отрезку АВ;
2. построить точку К пересечения отрезка АВ с плоскостью α;
3. отрезок СК перпендикулярен отрезку АВ.