- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параметры полета ракеты презентация
Содержание
- 1. Параметры полета ракеты
- 2. Понятие о математическом моделировании движения ракет
- 3. Для решения практических задач могут использоваться как
- 4. подготовка и проведение летного эксперимента приводит
- 5. - большие временные затраты на подготовку и проведение каждого эксперимента.
- 6. При решении практических задач баллистики ракет физическое
- 7. Такое математическое моделирование иногда называют «электронным выстрелом»,
- 8. Методы математического моделирования, кроме автоматизации численного анализа
- 9. При таком частичном эксперименте дорогостоящие приборы системы управления не уничтожаются, а остаются невредимыми.
- 10. Однако полет ракет и их БЧ является
- 11. В связи с этим для математического моделирования
- 12. Математическая модель движения представляет собой объективную схематизацию
- 13. Такой формой обычно являются: системы дифференциальных
- 14. Конкретный вид математической модели движения определяется принятыми
- 15. Выбор модели движения диктуется задачами проводимых исследований
- 16. Этим же обстоятельством объясняется и наличие большого
- 17. Все эти модели можно разделить на два вида: детерминированные и стохастические.
- 18. К детерминированным моделям относят модели, для которых
- 19. К стохастическим относят модели, для которых связь
- 20. Как детерминированные, так и стохастические модели могут
- 21. Для проведения математического моделирования полета модель движения
- 22. В целом численное моделирование полета предполагает последовательное выполнение следующих основных операций:
- 23. 1. Схематизация полета, включающая в себя схематизацию
- 24. 2. Запись уравнений движения в скалярной форме
- 25. 4. Задание исходных данных по ракете
- 26. 5. Задание системы возможных ограничений или связей
- 27. 6. Выбор и обоснование метода численного интегрирования
- 28. 7. Обоснование необходимого количества численных экспериментов для
- 29. 8. Проведение численных экспериментов и представление их
- 30. В зависимости от конкретной технической задачи, решаемой
- 31. Полет и его характеристики
- 32. Полет – это движение материального тела, называемого
- 33. Для полета реальный ЛА должен быть представлен
- 34. Такое представление ЛА называется схематизацией. Будем исходить
- 35. В качестве полюса может быть выбрана произвольная
- 36. Поступательным движением твердого тела называют такое движение,
- 37. Вращательным движением твердого тела называется движение, при
- 38. Физические величины, характеризующие положение и ориентацию ЛА
- 39. При этом величины, характеризующие движение центра масс
- 40. В общем случае параметры движения отражают его
- 41. Под геометрическими параметрами понимают параметры движения, характеризующие
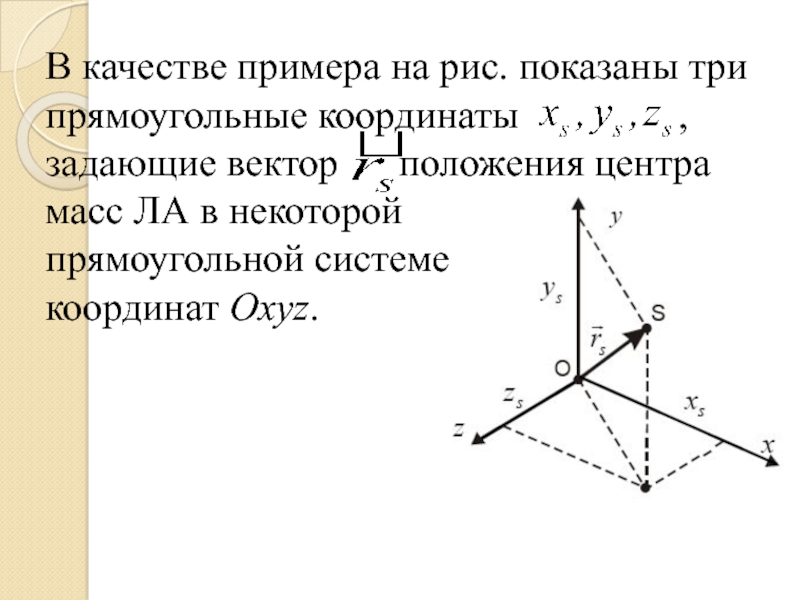
- 42. В качестве примера на рис. показаны три
- 43. Кинематические параметры движения характеризуют кинематические свойства полета
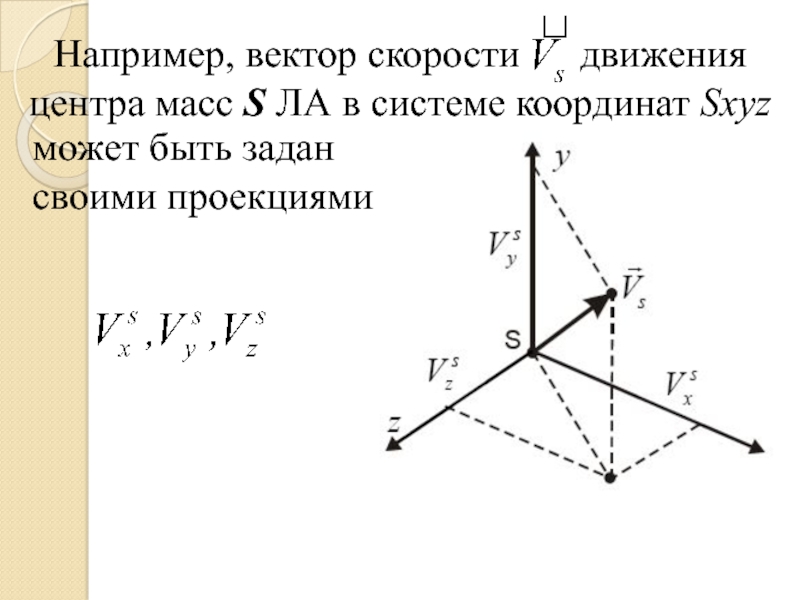
- 44. Например, вектор скорости движения центра
- 45. Динамические параметры движения отражают динамические свойства полета,
- 46. Геометрические параметры движения являются интегральными по отношению
- 47. Все они связаны между собой дифференциальными зависимостями
- 48. При математическом описании и анализе полета используется
- 49. Под числом степеней свободы понимают минимальное число
- 50. Независимость параметров следует понимать в том смысле,
- 51. Движение ЛА можно считать кинематически заданным, если известен закон изменения параметров движения во времени (2)
- 52. Однако в силу дифференциальной зависимости между геометрическими,
- 53. Уравнения движения являются основной частью математической модели
- 54. Получающаяся в результате система обыкновенных дифференциальных уравнений
- 55. Зависимые переменные
- 56. Соответствующая числу степеней свободы совокупность независимых параметров состояния образует пространство состояний или фазовое пространство.
- 57. Пространство состояний является математическим обобщением общеизвестного трехмерного
- 58. Для конечномерных механических систем, движение которых описывается
- 59. Подходы к математическому описанию полета
- 60. Математическое описание полета как частного вида механического
- 61. . Этот подход называют еще силовым подходом.
- 62. Подход очень нагляден, дает представление о механизме
- 63. Подход применим как для свободных систем, так
- 64. Этот подход называют энергетическим, так как в
- 65. Сущность подхода заключается в записи дифференциальных уравнений
- 66. Основные трудности этого подхода состоят в определении
- 67. Этот подход основан на использовании канонических уравнений
- 68. В итоге применения формализма Гамильтона получаются сразу скалярные уравнения в нормальной форме.
- 69. Получаемая в результате использования этих подходов механики
- 70. Для моделирования управляемого движения ЛА, снабженного СУ,
- 71. Для записи уравнений работы системы управления используются методы теории автоматического управления.
Понятие о математическом моделировании движения ракет
Слайд 3Для решения практических задач могут использоваться как теоретические, так и экспериментальные
методы.
В баллистике ракет использование летного эксперимента для решения таких задач весьма ограничено и часто в принципе невозможно.
Это обусловлено следующими обстоятельствами:
Слайд 4 подготовка и проведение летного эксперимента приводит к фактическому уничтожению испытуемого
образца ракеты;
- большие материальные затраты на проведение летного эксперимента;
большие дальности полета, при которых ни запланированная цель, ни реальная точка падения БЧ не видны;
большое влияние возмущающих факторов, различное при каждом пуске, что исключает возможность пролонгации их влияния на последующие пуски;
- большие материальные затраты на проведение летного эксперимента;
большие дальности полета, при которых ни запланированная цель, ни реальная точка падения БЧ не видны;
большое влияние возмущающих факторов, различное при каждом пуске, что исключает возможность пролонгации их влияния на последующие пуски;
Слайд 6При решении практических задач баллистики ракет физическое моделирование полета (летный эксперимент)
заменяется математическим моделированием, т. е. математическим расчетом параметров движения
Слайд 7Такое математическое моделирование иногда называют «электронным выстрелом», так как проводится на
ЭЦВМ.
В результате основным методом решения всех практических задач в баллистике ракет является метод математического моделирования полета при постановке минимального числа летных экспериментов.
В результате основным методом решения всех практических задач в баллистике ракет является метод математического моделирования полета при постановке минимального числа летных экспериментов.
Слайд 8Методы математического моделирования, кроме автоматизации численного анализа полета, позволяют сочетать теоретические
исследования с экспериментальными.
Они дают возможность проведения частичного эксперимента, т.е. такого эксперимента, в котором движение ракеты имитируется моделью, а система управления или отдельные ее приборы работают также, как и при действительном полете ракет.
Они дают возможность проведения частичного эксперимента, т.е. такого эксперимента, в котором движение ракеты имитируется моделью, а система управления или отдельные ее приборы работают также, как и при действительном полете ракет.
Слайд 9При таком частичном эксперименте дорогостоящие приборы системы управления не уничтожаются, а
остаются невредимыми.
Слайд 10Однако полет ракет и их БЧ является весьма сложным процессом так
как подвержен влиянию большого числа различных факторов – случайных, трудно поддающихся математическому описанию.
Поэтому любое математическое моделирование полета проводится лишь в некоторых идеализированных условиях.
Степень идеализации зависит от условий решаемой задачи и может быть различной.
Поэтому любое математическое моделирование полета проводится лишь в некоторых идеализированных условиях.
Степень идеализации зависит от условий решаемой задачи и может быть различной.
Слайд 11В связи с этим для математического моделирования полета ракет и БЧ
создаются специальные математические модели, отражающие реальный полет с различной степенью точности.
Слайд 12Математическая модель движения представляет собой объективную схематизацию действительного движения объекта в
форме, позволяющей проводить различные теоретические исследования и необходимые вычисления для решения поставленной задачи.
Слайд 13Такой формой обычно являются:
системы дифференциальных уравнений (обыкновенных или в частных
производных), разрабатываемые в рамках теоретической механики и имеющие смысл уравнений движения объекта;
системы конечных аналитических соотношений, если схема полета позволяет получить аналитическое решение уравнений движения.
системы конечных аналитических соотношений, если схема полета позволяет получить аналитическое решение уравнений движения.
Слайд 14Конкретный вид математической модели движения определяется принятыми при разработке модели схемами
ЛА как механической системы, внешней среды, определяющей силовое воздействие на ЛА, а также системы отсчета и выбранной системы координат.
Слайд 15Выбор модели движения диктуется задачами проводимых исследований и неоднозначен.
При этом
к моделям часто предъявляются противоречивые требования - адекватности, точности, простоты, наглядности и др.
Поэтому в каждой конкретной технической задаче обоснование и окончательный выбор модели является результатом компромисса и представляет собой важный этап процесса моделирования полета.
Поэтому в каждой конкретной технической задаче обоснование и окончательный выбор модели является результатом компромисса и представляет собой важный этап процесса моделирования полета.
Слайд 16Этим же обстоятельством объясняется и наличие большого числа различных математических моделей
движения, используемых при решении практических задач.
Слайд 18К детерминированным моделям относят модели, для которых силы и моменты, действующие на
объект, имеют только детерминированную составляющую.
Это означает, что характер зависимости этой составляющей от параметров движения, времени и условий полета известен заранее.
Это означает, что характер зависимости этой составляющей от параметров движения, времени и условий полета известен заранее.
Слайд 19К стохастическим относят модели, для которых связь между параметрами движения и
временем известна лишь приближенно и может быть представлена некоторым распределением вероятности.
Для таких моделей предполагается, что все или некоторые компоненты вектора характеристик, определяющих силы и моменты, действующие на объект, содержат случайную составляющую наряду с детерминированной.
Для таких моделей предполагается, что все или некоторые компоненты вектора характеристик, определяющих силы и моменты, действующие на объект, содержат случайную составляющую наряду с детерминированной.
Слайд 20Как детерминированные, так и стохастические модели могут быть представлены в дифференциальном или
конечном аналитическом виде в зависимости от того, допускают или не допускают дифференциальные уравнения движения объекта получение конечного аналитического решения.
Слайд 21Для проведения математического моделирования полета модель движения должна быть дополнена начальными
условиями, определяющими начальное состояние ракеты, или соотношениями для их расчета, системой ограничений или связей, определяющих множество допустимых значений параметров движения, параметров ракеты и ее системы управления, а также условиями или алгоритмом определения конечного состояния, т. е. окончания процесса моделирования.
Слайд 22В целом численное моделирование полета предполагает последовательное выполнение следующих основных операций:
Слайд 231. Схематизация полета, включающая в себя схематизацию ракеты как механической системы,
системы отсчета и условий полета, а также схематизацию системы управления полетом.
Слайд 242. Запись уравнений движения в скалярной форме при соответствующем выборе систем
координат.
3. Задание начальных условий для системы дифференциальных уравнений движения или соотношений для их расчета.
3. Задание начальных условий для системы дифференциальных уравнений движения или соотношений для их расчета.
Слайд 25 4. Задание исходных данных по ракете и ее системе управления,
включающих энергетические, массово-инерционные, аэродинамические, геометрические и другие характеристики.
Слайд 265. Задание системы возможных ограничений или связей на параметры движения или
параметры управления, определяющих область их допустимых значений.
Слайд 276. Выбор и обоснование метода численного интегрирования уравнений движения или аналитических представлений
полета на отдельных участках траектории, величины шага интегрирования
на активном и пассивном участках траектории и условий окончания процесса моделирования.
Слайд 287. Обоснование необходимого количества численных экспериментов для выявления требуемых закономерностей полета
или получения решения поставленной задачи.
Слайд 298. Проведение численных экспериментов и представление их результатов в требуемой по
условиям задачи форме с указанием границ или рамок их возможного использования.
Слайд 30В зависимости от конкретной технической задачи, решаемой путем моделирования полета, содержание
вышеуказанных этапов может быть конкретизировано или дополнено другими операциями.
Слайд 32Полет – это движение материального тела, называемого ЛА, над поверхностью Земли
в атмосфере или за ее пределами в космическом пространстве.
Полет является частным видом механического движения, называемого перемещением материального тела в пространстве и во времени.
Для задания полета, его математического описания и характеристики могут быть использованы основные понятия и подходы теоретической механики.
Полет является частным видом механического движения, называемого перемещением материального тела в пространстве и во времени.
Для задания полета, его математического описания и характеристики могут быть использованы основные понятия и подходы теоретической механики.
Слайд 33Для полета реальный ЛА должен быть представлен в виде некоторого абстрактного механического
объекта (материальная точка, система материальных точек, твердое тело и т. д.), к которому применимы общие законы механики.
Слайд 34Такое представление ЛА называется схематизацией.
Будем исходить из того, что ракета или
ее БЧ могут быть представлены схемой твердого тела.
В теоретической механике произвольное перемещение твердого тела представляется в виде совокупности поступательного движения некоторого полюса и вращательного движения тела относительно этого полюса.
В теоретической механике произвольное перемещение твердого тела представляется в виде совокупности поступательного движения некоторого полюса и вращательного движения тела относительно этого полюса.
Слайд 35В качестве полюса может быть выбрана произвольная точка тела.
Обычно в качестве
полюса принимают ЦМ тела.
В этом случае уравнения движения имеют наиболее простой вид.
В этом случае уравнения движения имеют наиболее простой вид.
Слайд 36Поступательным движением твердого тела называют такое движение, при котором любая прямая,
проведенная в этом теле, перемещается параллельно самой себе.
При этом движении скорости и ускорения всех точек тела для любого момента времени равны между собой.
Поэтому движение ЛА может быть полностью определено движением одной точки, например, движением ЦМ.
При этом движении скорости и ускорения всех точек тела для любого момента времени равны между собой.
Поэтому движение ЛА может быть полностью определено движением одной точки, например, движением ЦМ.
Слайд 37Вращательным движением твердого тела называется движение, при котором какие-либо две точки
тела остаются неподвижными в каждый текущий момент времени,
т. е. происходит вращение тела вокруг некоторой мгновенной оси.
т. е. происходит вращение тела вокруг некоторой мгновенной оси.
Слайд 38Физические величины, характеризующие положение и ориентацию ЛА в пространстве и их
изменение во времени, называют параметрами движения.
Как правило, к ним относят линейные и угловые координаты, составляющие векторов линейных и угловых скоростей и ускорений ЛА в той или иной системе координат.
Как правило, к ним относят линейные и угловые координаты, составляющие векторов линейных и угловых скоростей и ускорений ЛА в той или иной системе координат.
Слайд 39При этом величины, характеризующие движение центра масс ЛА, называют параметрами поступательного
движения, а величины, характеризующие движение ЛА вокруг ЦМ - параметрами
вращательного движения.
Слайд 40В общем случае параметры движения отражают его различные стороны и в
соответствии с этим подразделяются на геометрические, кинематические и динамические.
Слайд 41Под геометрическими параметрами понимают параметры движения, характеризующие геометрические свойства полета и
определяющие составляющие вектора положения ЛА в некоторой системе координат.
Это параметры ориентации ЛА (углы Эйлера, направляющие косинусы и т. д.) в заданный момент времени.
Это параметры ориентации ЛА (углы Эйлера, направляющие косинусы и т. д.) в заданный момент времени.
Слайд 42В качестве примера на рис. показаны три прямоугольные координаты
, задающие вектор положения центра
масс ЛА в некоторой прямоугольной системе координат Oxyz.
Слайд 43Кинематические параметры движения характеризуют кинематические свойства полета ЛА без учета его
массово-
инерционных характеристик и действующих на ЛА сил и определяют компоненты векторов линейной и угловой скоростей ЛА в различных системах координат.
Слайд 44Например, вектор скорости движения центра масс S ЛА в
системе координат Sxyz
может быть задан своими проекциями
Слайд 45Динамические параметры движения отражают динамические свойства полета, обусловленные действующими на ЛА
силами и моментами и его массово-инерционными характеристиками, и определяют компоненты векторов линейного и углового ускорений ЛА.
Слайд 46Геометрические параметры движения являются интегральными по отношению к кинематическим параметрам.
Кинематические параметры
являются интегральными по отношению к динамическим параметрам.
Слайд 47Все они связаны между собой дифференциальными зависимостями
где - вектор
параметров угловой ориентации ЛА в пространстве; - вектор угловой скорости ЛА; - векторы линейного и углового ускорений.
Слайд 48При математическом описании и анализе полета используется большое число различных параметров
движения, задаваемых в различных СК.
Однако число независимых параметров в каждой из названных групп определяется числом степеней свободы ракеты.
Однако число независимых параметров в каждой из названных групп определяется числом степеней свободы ракеты.
Слайд 49Под числом степеней свободы понимают минимальное число независимых параметров (координат), однозначно
определяющих положение тела в пространстве.
Слайд 50Независимость параметров следует понимать в том смысле, что ни один из
них не может быть выражен через другие.
Для материальной точки число степеней свободы равно трем, так как ее положение в пространстве можно однозначно задать с помощью трех координат.
Абсолютно твердое тело имеет шесть степеней свободы: три степени свободы поступательного движения и три - вращательного движения.
Для материальной точки число степеней свободы равно трем, так как ее положение в пространстве можно однозначно задать с помощью трех координат.
Абсолютно твердое тело имеет шесть степеней свободы: три степени свободы поступательного движения и три - вращательного движения.
Слайд 51Движение ЛА можно считать кинематически заданным, если известен закон изменения параметров движения
во времени
(2)
Слайд 52Однако в силу дифференциальной зависимости между геометрическими, кинематическими и динамическими параметрами
движения установить этот закон можно только через дифференциальные уравнения, которые называют уравнениями движения.
Слайд 53Уравнения движения являются основной частью математической модели движения.
Задача записи этих уравнений
представляет собой задачу математического описания полета.
Слайд 54Получающаяся в результате система обыкновенных дифференциальных уравнений движения, приведенная к нормальной
форме, обычно записывается в следующем стандартном функциональном виде:
(3)
где
n - порядок системы уравнении, равный удвоенному числу степеней свободы ЛА;
t - время, являющееся независимой переменной;
- неизвестные переменные, зависимые от времени; - первые производные по времени от соответствующих переменных.
Слайд 55 Зависимые переменные
представляют собой линейные и угловые координаты и составляющие векторов линейной и угловой скоростей ЛА, т.е. совокупность геометрических и кинематических параметров движения.
Они полностью определяют положение ЛА и его скорость в текущий момент времени, поэтому их также называют параметрами состояния, или фазовыми координатами.
Они полностью определяют положение ЛА и его скорость в текущий момент времени, поэтому их также называют параметрами состояния, или фазовыми координатами.
Слайд 56Соответствующая числу степеней свободы совокупность независимых параметров состояния образует пространство состояний или
фазовое пространство.
Слайд 57Пространство состояний является математическим обобщением общеизвестного трехмерного физического пространства и распространяет
понятие координаты точки в трехмерном пространстве на более общее понятие фазовой координаты точки.
Слайд 58Для конечномерных механических систем, движение которых описывается системой уравнений вида (3),
пространство состояний представляется как n-мерное координатное пространство, в котором все величины полностью равноправны независимо от их физического смысла и физической размерности.
Слайд 60Математическое описание полета как частного вида механического движения основывается на общих
законах и теоремах теоретической механики.
Для этой цели в общем случае могут быть использованы подходы механики Ньютона, механики Лагранжа и механики Гамильтона.
Для этой цели в общем случае могут быть использованы подходы механики Ньютона, механики Лагранжа и механики Гамильтона.
Слайд 61. Этот подход называют еще силовым
подходом.
Он опирается на понятие силы
и основные теоремы динамики точки и твердого тела, на основе которых записываются исходные векторные уравнения движения ЦМ и вокруг ЦМ.
Подход механики Ньютона
Слайд 62Подход очень нагляден, дает представление о механизме воздействия каждой из сил
на движение ЛА, достаточно прост для механических схем ЛА в виде материальной точки или твердого тела, но более сложен в случае составных механических систем, Основная трудность подхода заключается в переходе от векторных уравнений к скалярным, т. е. в проектировании исходных векторных уравнений на оси выбранных СК.
Слайд 63Подход применим как для свободных систем, так и для систем со
связями.
В последнем случае связи заменяются реакциями связей, т. е. в число действующих сил добавляются силы реакции связей.
В последнем случае связи заменяются реакциями связей, т. е. в число действующих сил добавляются силы реакции связей.
Слайд 64Этот подход называют энергетическим, так как в его основе лежат понятие
энергии и дифференциальные уравнения Лагранжа П рода.
Формализм Лагранжа позволяет получить сразу скалярные уравнения, т. е. исключает операцию проектирования векторных уравнений.
Формализм Лагранжа позволяет получить сразу скалярные уравнения, т. е. исключает операцию проектирования векторных уравнений.
Подход механики Лагранжа.
Слайд 65Сущность подхода заключается в записи дифференциальных уравнений Лагранжа II рода для
обобщенных координат и обобщенных скоростей в следующей последовательности:
где
Т - кинетическая энергия; - обобщенные координаты и обобщенные скорости; - обобщенные силы; N - число степеней свободы.
Слайд 66Основные трудности этого подхода состоят в определении обобщенных сил.
Подход удобен
для записи уравнений движения составных механических систем.
Слайд 67Этот подход основан на использовании канонических уравнений Гамильтона для обобщенных фазовых
координат и обобщенных импульсов :
где - гамильтониан;
- функция Лагранжа; Т - кинетическая энергия системы; U - потенциальная энергия системы.
где - гамильтониан;
- функция Лагранжа; Т - кинетическая энергия системы; U - потенциальная энергия системы.
Подход механики Гамильтона.
Слайд 68В итоге применения формализма Гамильтона получаются сразу скалярные уравнения в нормальной
форме.
Слайд 69Получаемая в результате использования этих подходов механики система скалярных уравнений определяет
механическое движение самого ЛА как механического объекта без учета работы СУ.
Слайд 70Для моделирования управляемого движения ЛА, снабженного СУ, полученную систему уравнений необходимо
дополнить уравнениями работы системы управления.
Система управления определяют управляющие воздействия в виде управляющих сил и моментов, с помощью которых и осуществляется управление полетом.
Система управления определяют управляющие воздействия в виде управляющих сил и моментов, с помощью которых и осуществляется управление полетом.
Слайд 71Для записи уравнений работы системы управления используются методы теории автоматического управления.
