- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов презентация
Содержание
- 1. Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов
- 2. Две прямые называются параллельными, если они не пересекаются. b a Обозначают: a || b
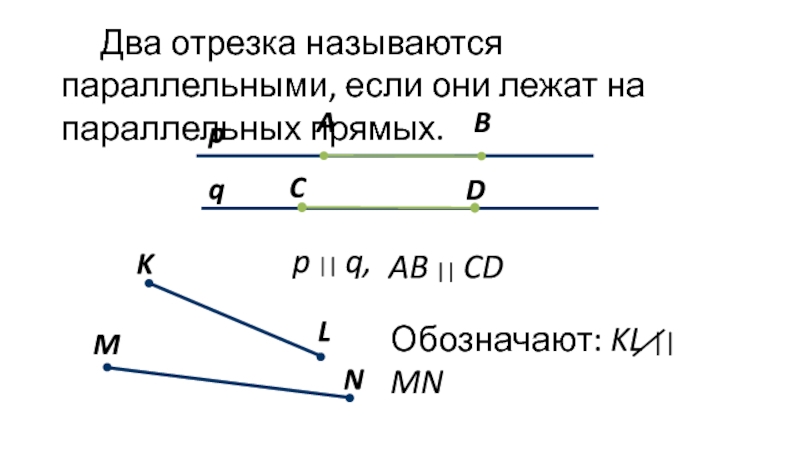
- 3. Два отрезка называются параллельными, если они лежат
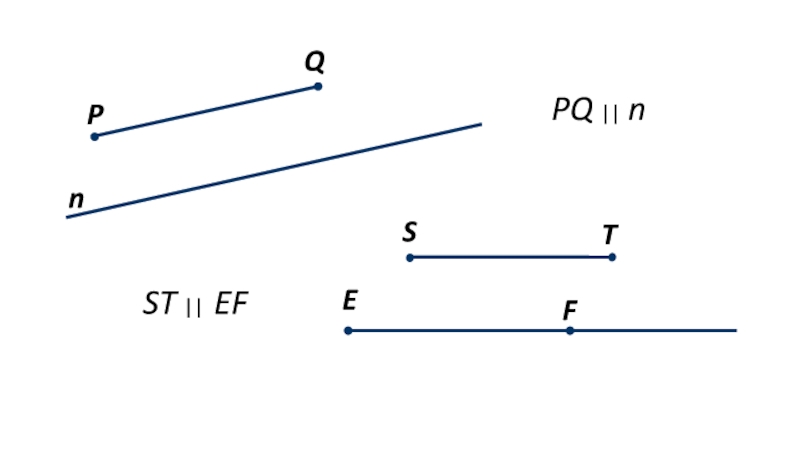
- 4. Q P n PQ || n T S E F ST || EF
- 5. a b c a || b
- 6. 1 3 4 2 5
- 7. a b c 1 3
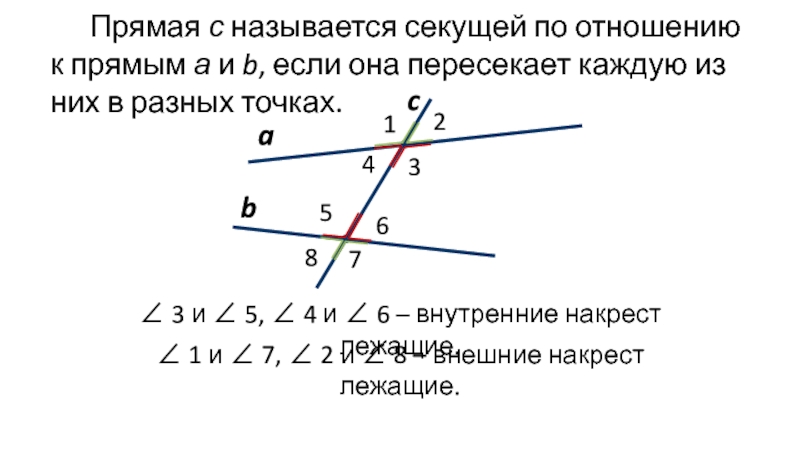
- 8. Теорема. Если при пересечении двух прямых секущей
- 9. Задача. Докажите, что если два отрезка KL
- 10. а || b
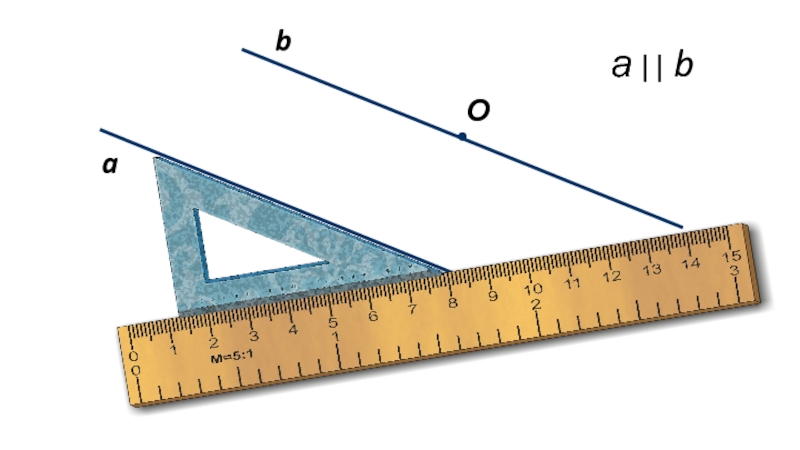
- 11. Рейсшина
- 12. Малка
Слайд 3Два отрезка называются параллельными, если они лежат на параллельных прямых.
q
p
B
A
D
p ||
AB || CD
K
L
M
N
C
Слайд 6
1
3
4
2
5
6
7
8
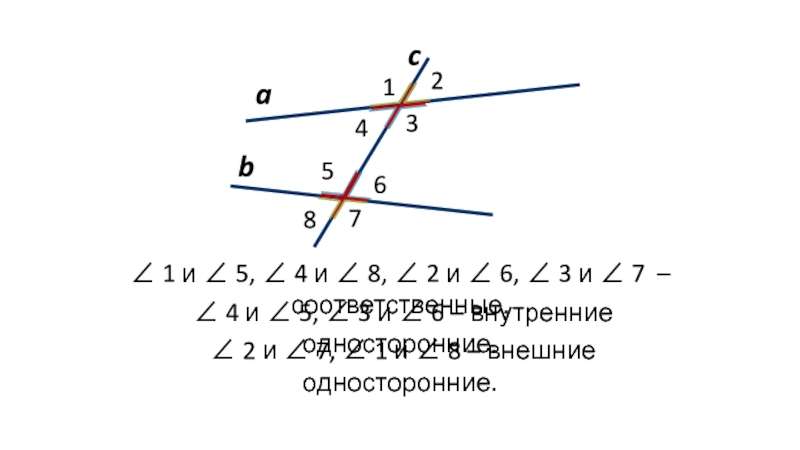
∠ 3 и ∠ 5, ∠ 4 и ∠ 6 –
∠ 1 и ∠ 7, ∠ 2 и ∠ 8 – внешние накрест лежащие.
Слайд 7a
b
c
1
3
4
2
5
6
7
8
∠ 4 и ∠ 5, ∠ 3 и ∠ 6
∠ 1 и ∠ 5, ∠ 4 и ∠ 8, ∠ 2 и ∠ 6, ∠ 3 и ∠ 7 – соответственные.
∠ 2 и ∠ 7, ∠ 1 и ∠ 8 – внешние односторонние.
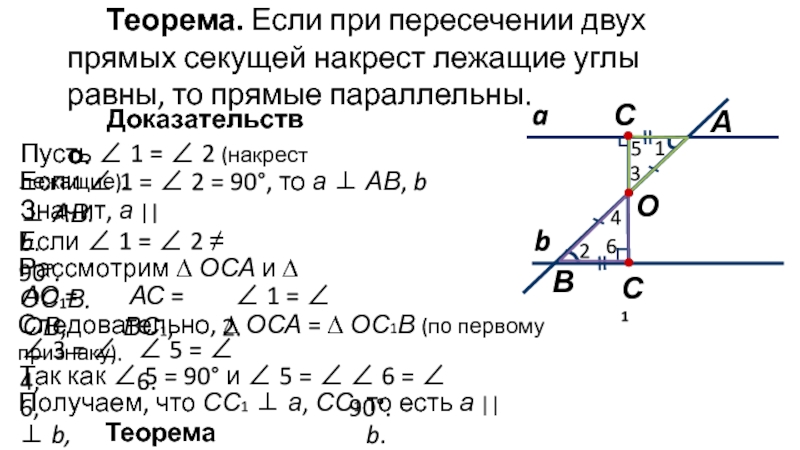
Слайд 8Теорема. Если при пересечении двух прямых секущей накрест лежащие углы равны,
Доказательство.
Если ∠ 1 = ∠ 2 = 90°, то а ⊥ АВ, b ⊥ АВ.
Значит, а || b.
Если ∠ 1 = ∠ 2 ≠ 90°.
Рассмотрим ∆ ОСА и ∆ ОС1В.
АО = ОВ,
АС = ВС1,
∠ 1 = ∠ 2.
Следовательно, ∆ ОСА = ∆ ОС1В (по первому признаку).
Так как ∠ 5 = 90° и ∠ 5 = ∠ 6,
Получаем, что СС1 ⊥ а, СС1 ⊥ b,
то есть а || b.
Теорема доказана.
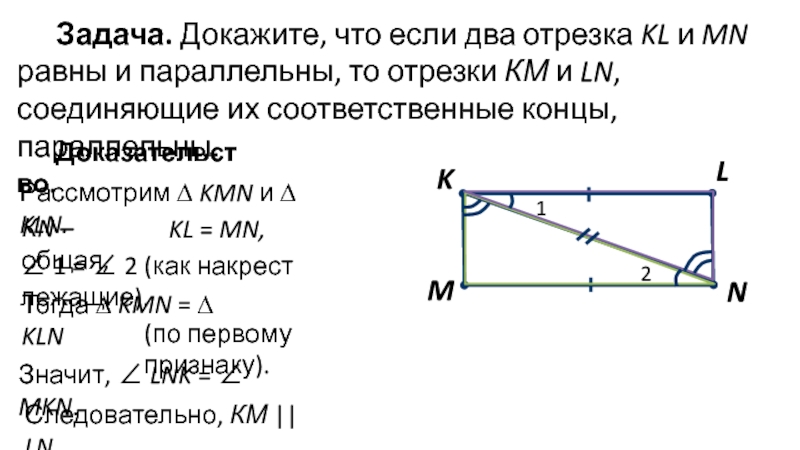
Слайд 9Задача. Докажите, что если два отрезка KL и MN равны и
Доказательство.
K
N
M
L
Рассмотрим ∆ KMN и ∆ KLN.
КN – общая,
KL = MN,
∠ 1 = ∠ 2 (как накрест лежащие).
1
2
Тогда ∆ KMN = ∆ KLN
(по первому признаку).
Значит, ∠ LNK = ∠ MKN.
Следовательно, КМ || LN.