- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллелепипед. Тетраэдр. Виды многогранников презентация
Содержание
- 1. Параллелепипед. Тетраэдр. Виды многогранников
- 2. КОНУС
- 3. Понятие многогранника Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранником. Примеры многогранников
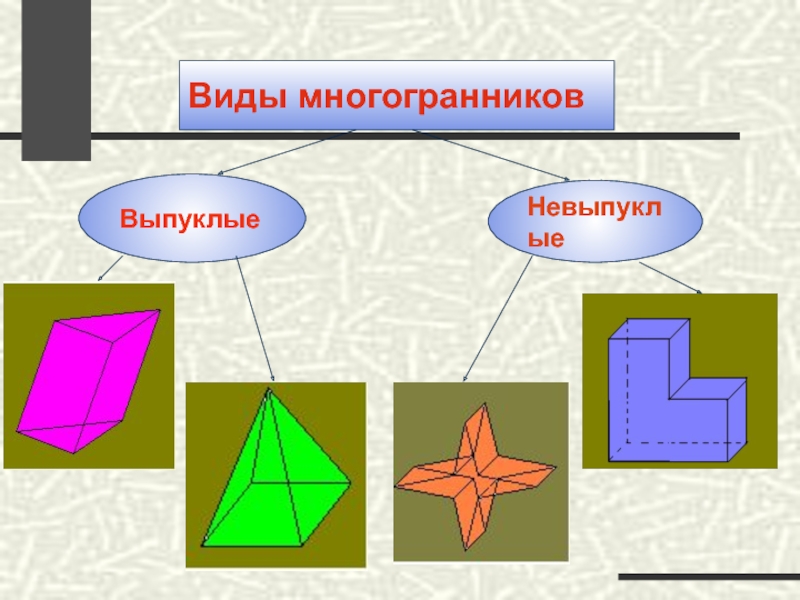
- 4. Виды многогранников Выпуклые Невыпуклые
- 5. Примеры многогранников Большой курносый икосододекаэдр
- 6. Примеры многогранников Большой ромбогексаэдр
- 7. Примеры многогранников Квазиромбокубоктаэдр
- 8. Выпуклый многогранник Многогранник называется выпуклым, если
- 9. Призма Призмой называется многогранник, который состоит из
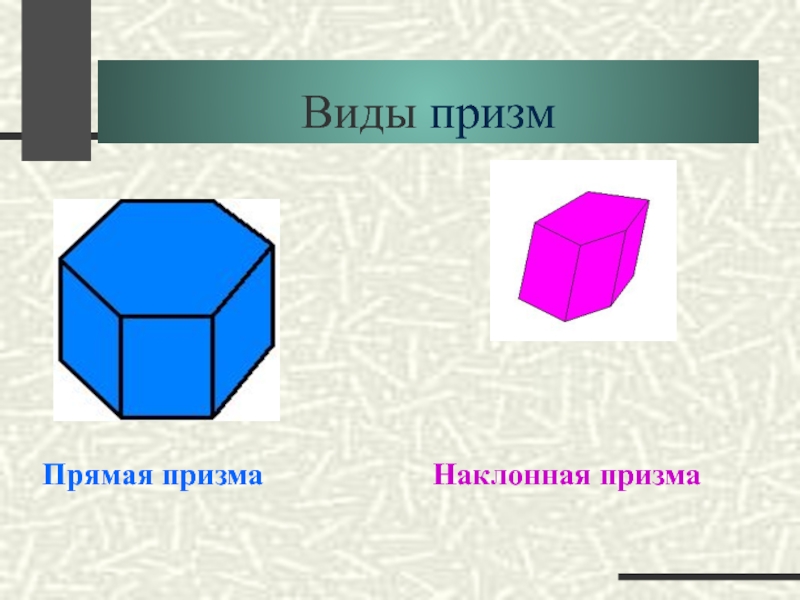
- 10. Виды призм Прямая призма Наклонная призма
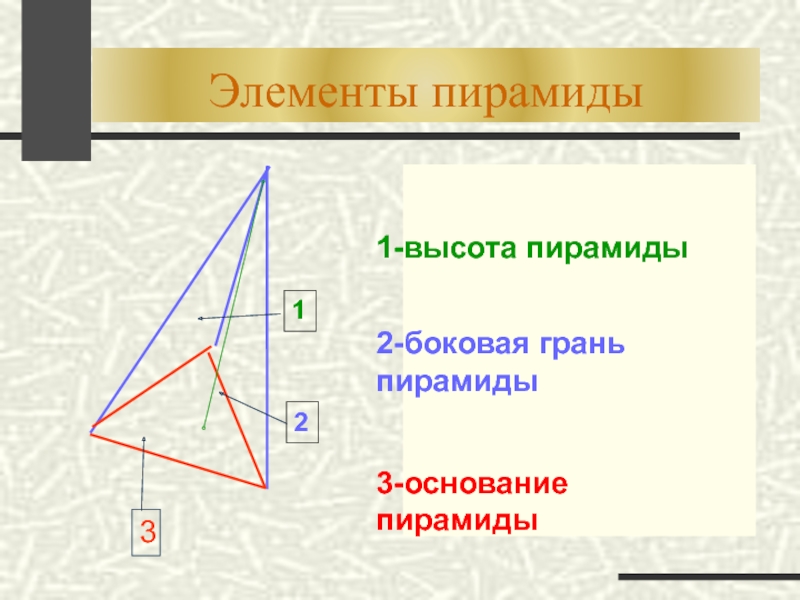
- 11. Пирамида Многогранник, составленный из
- 12. Элементы пирамиды 1-высота
- 13. Гексаэдр Куб составлен из шести квадратов. Каждая
- 14. Тетраэдр Тетраэдр составлен из четырех равносторонних треугольников.
- 15. Октаэдр Октаэдр составлен из восьми равносторонних треугольников.
- 16. Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников.
- 17. Икосаэдр Икосаэдр составлен из двадцати равносторонних треугольников.
- 18. D А
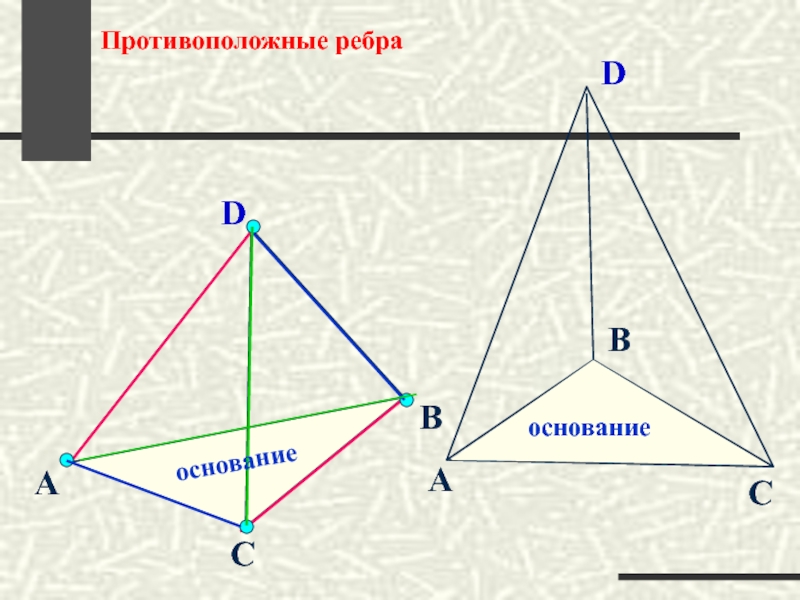
- 20. D А С В Противоположные ребра основание основание
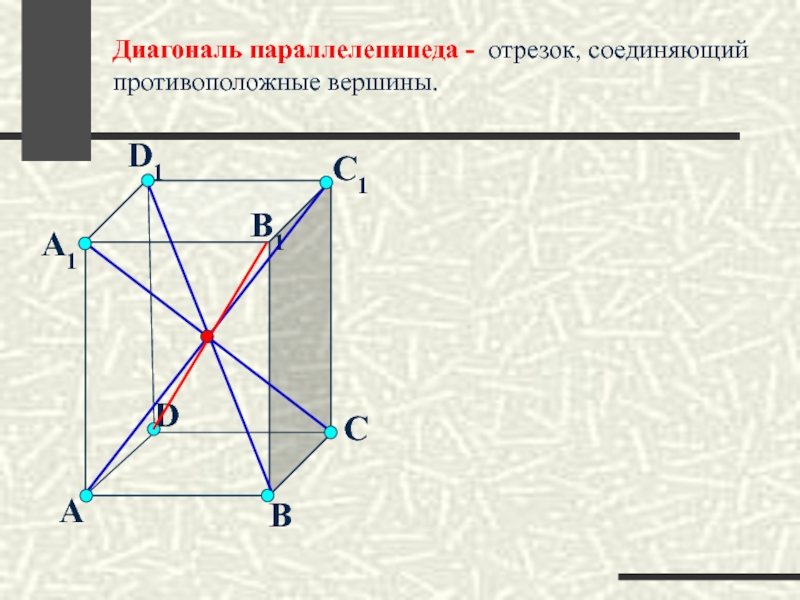
- 21. А В С D А1 D1
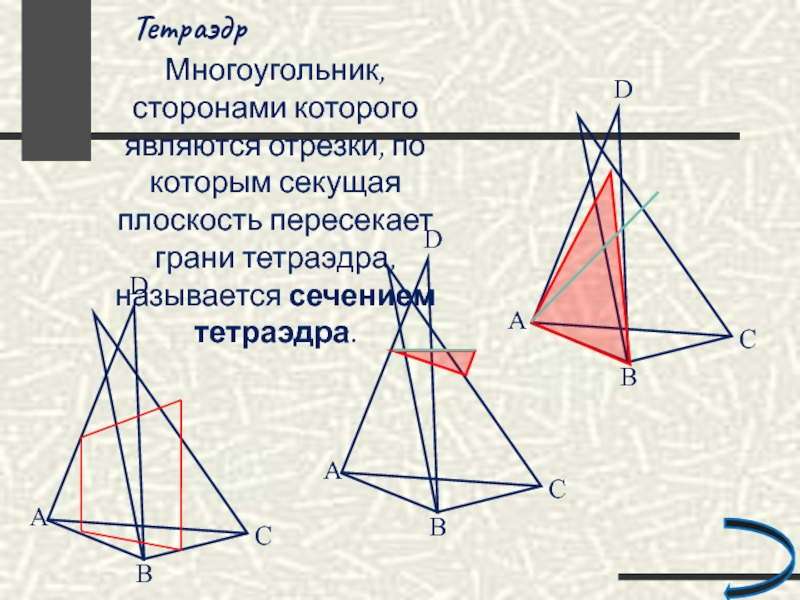
- 22. Тетраэдр C A D B Многоугольник, сторонами
- 23. Параллелепипед Многоугольник, сторонами которого являются отрезки, по
- 25. Правила построения сечений ТЕТРАЭДРА а)Проводим прямые
- 26. А B D C N M
- 27. А B D C N M
- 28. Построение сечения тетраэдра через точки M,
- 29. Построение сечения тетраэдра через точки M,
- 30. Построение сечения тетраэдра через точки M,
- 31. Построение сечения тетраэдра через точки M,
- 32. Секущей плоскостью тетраэдра называют любую плоскость,
- 33. Сечение тетраэдра - выпуклый многоугольник, вершинами
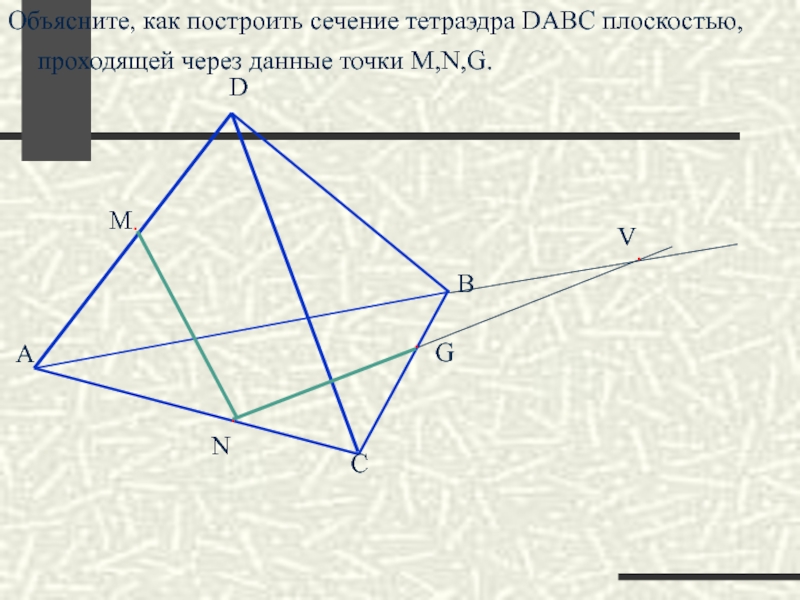
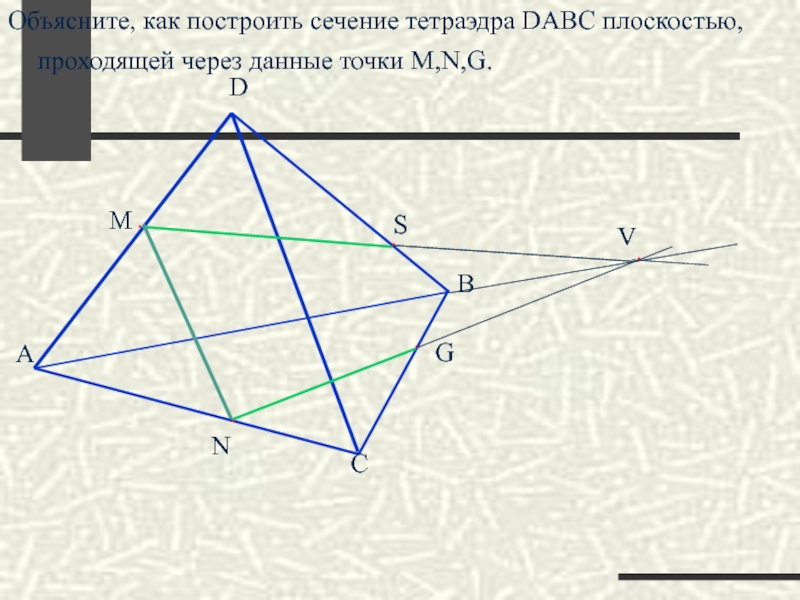
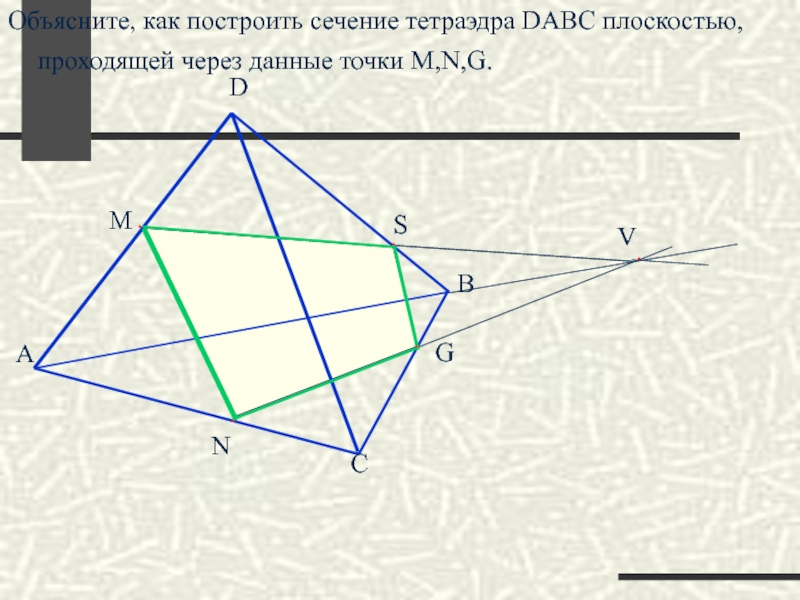
- 34. Построить сечение тетраэдра DABC плоскостью, проходящей через
- 35. А D B C Е М К ∙ ∙ ∙
- 36. Построить сечение тетраэдра DABC плоскостью, проходящей
- 37. Построить сечение тетраэдра DABC плоскостью, проходящей
- 38. Задание Построить сечение тетраэдра ABCD, проходящее
- 42. ∙
- 45. А С В D N P
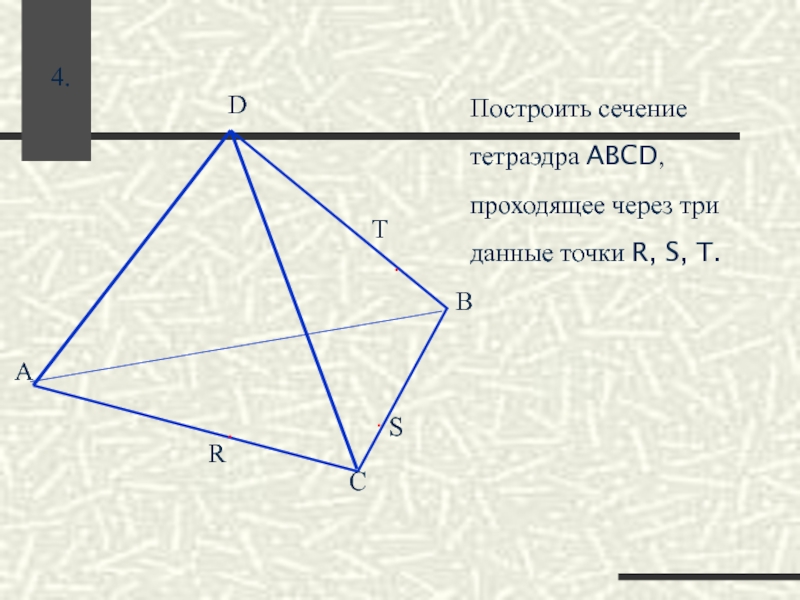
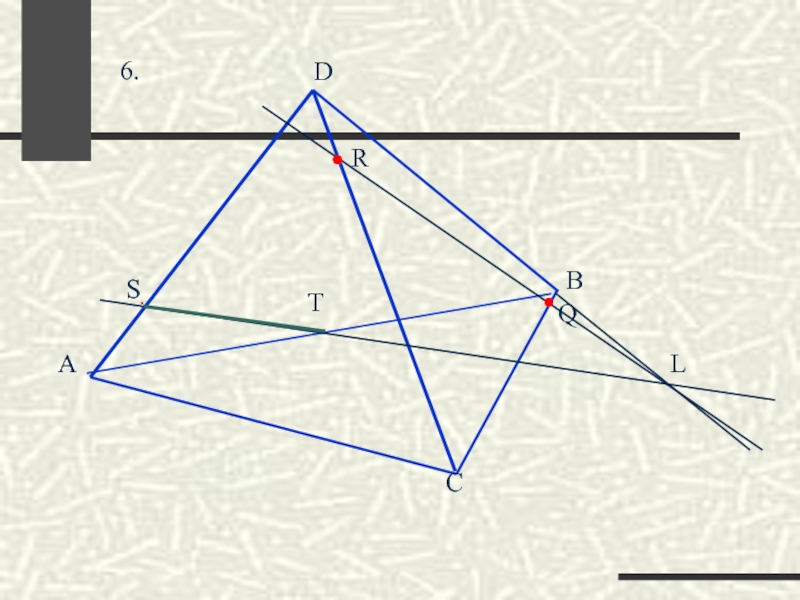
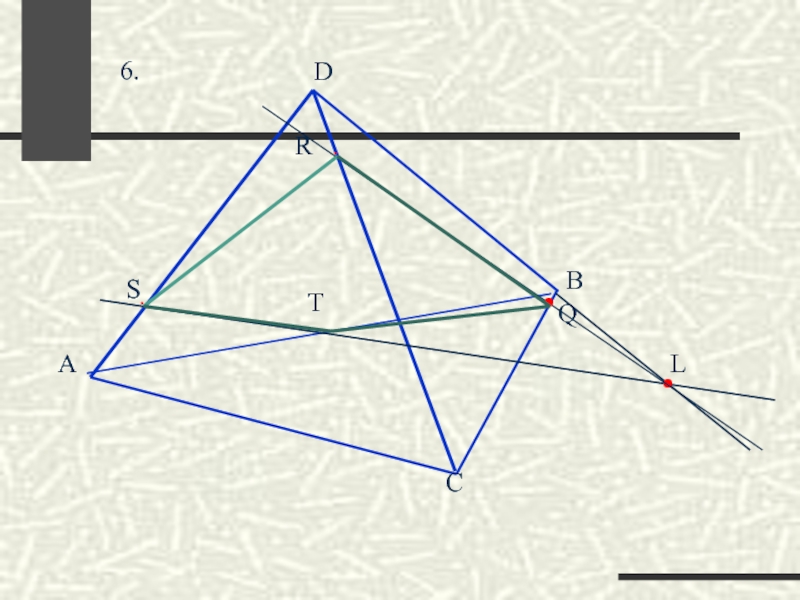
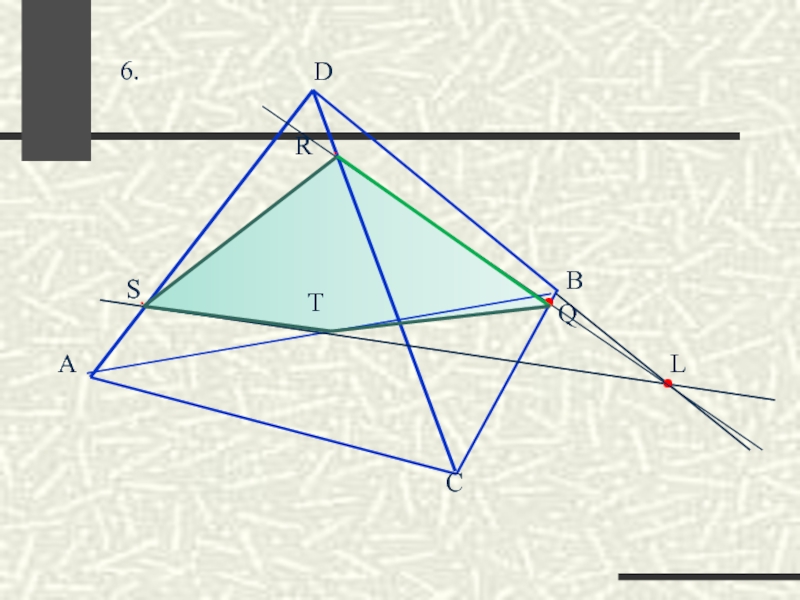
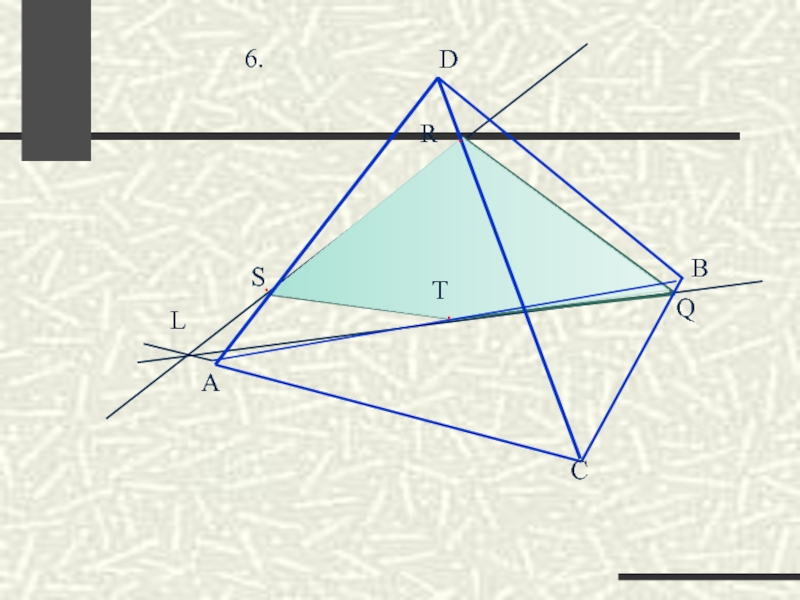
- 46. Построить сечение тетраэдра ABCD, проходящее через три данные точки R, S, T.
- 47. ∙ ∙ R T
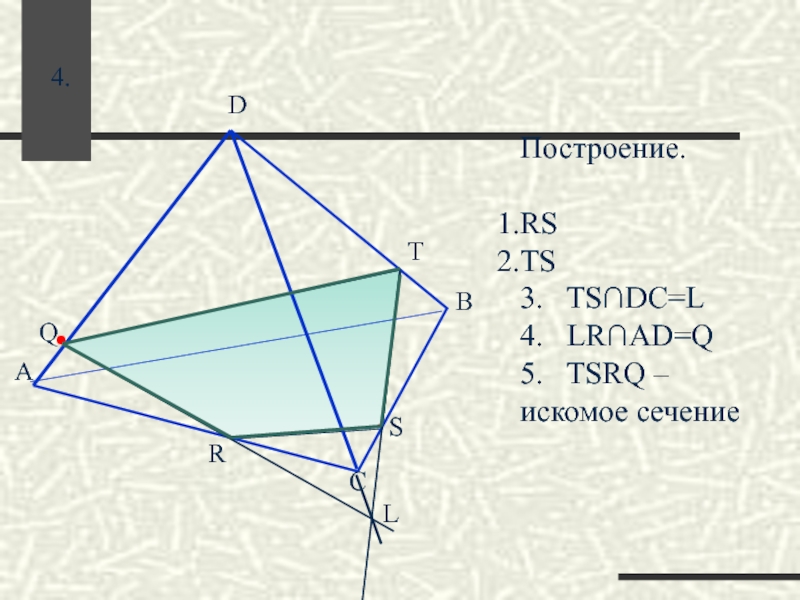
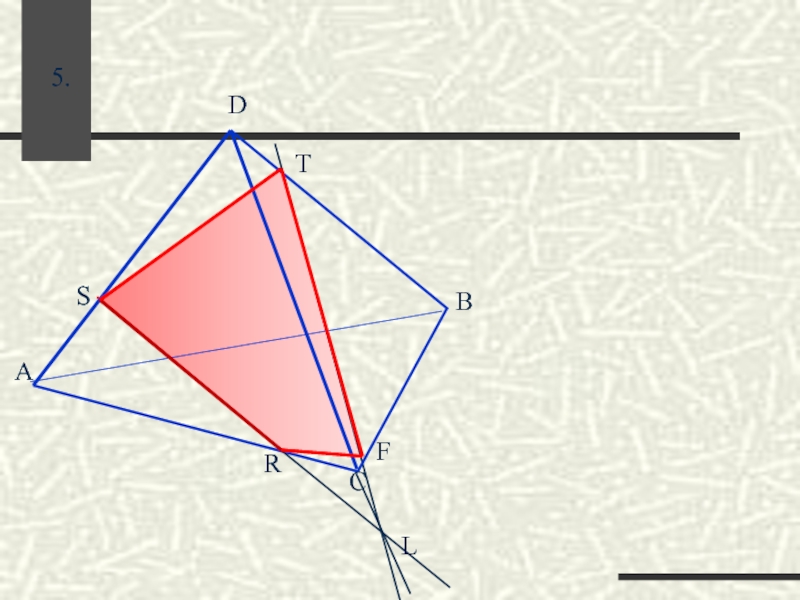
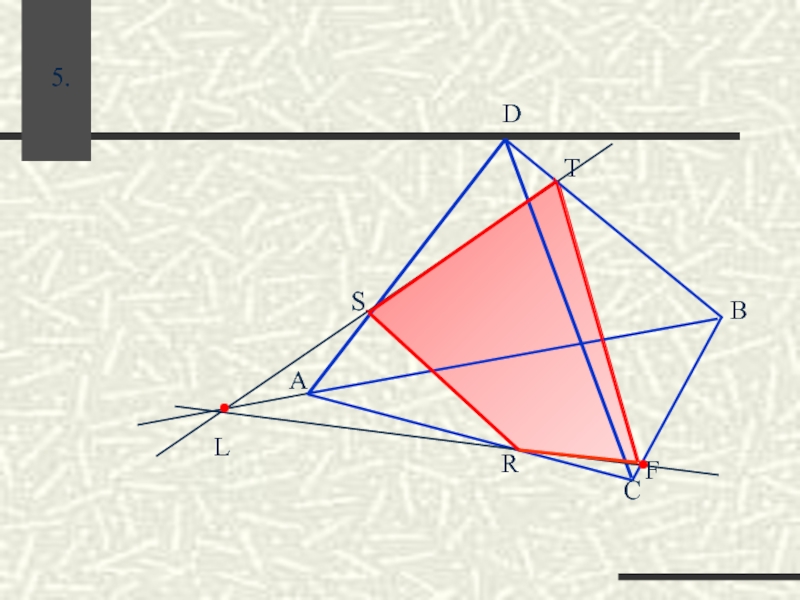
- 48. ∙ ∙ R T S ∙ 5. L F
- 49. ∙ ∙ R T S ∙ 5. . F .L
- 50. L . Q . R
- 51. . L . Q
- 52. . L . Q
- 53. L
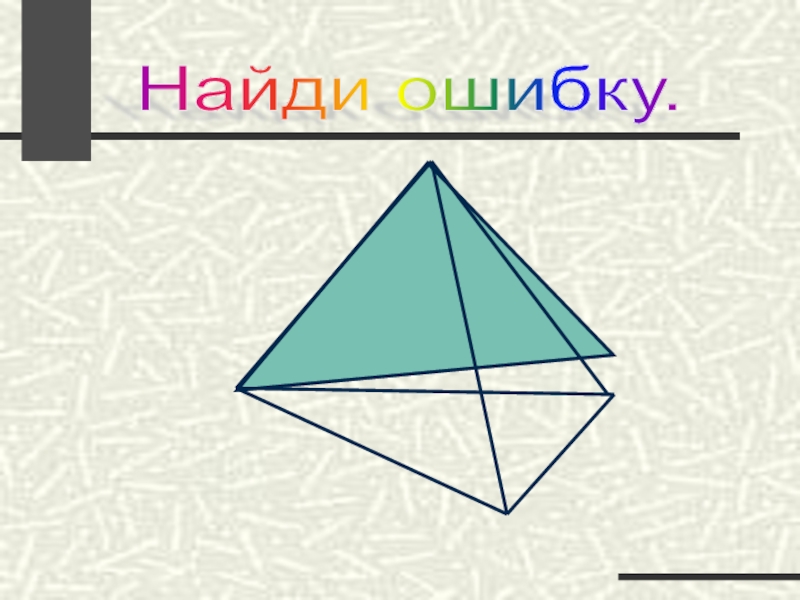
- 54. Найди ошибку.
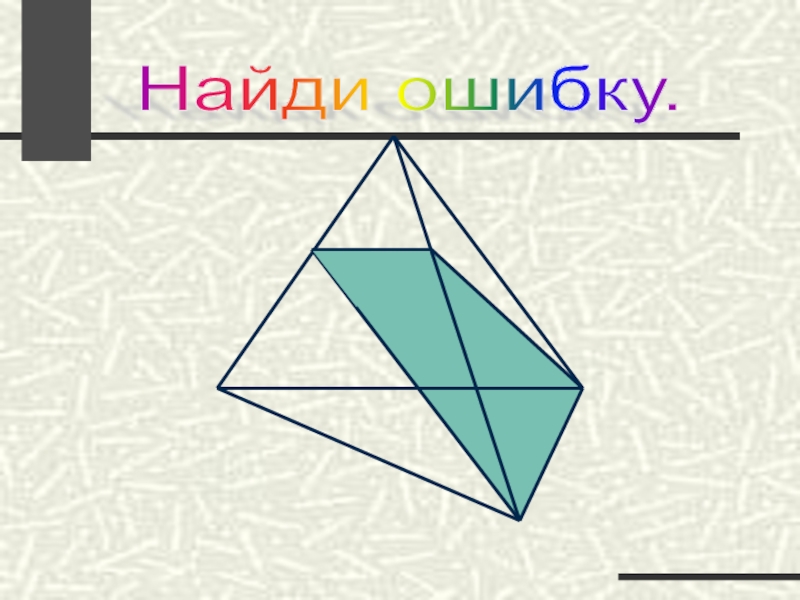
- 55. Найди ошибку.
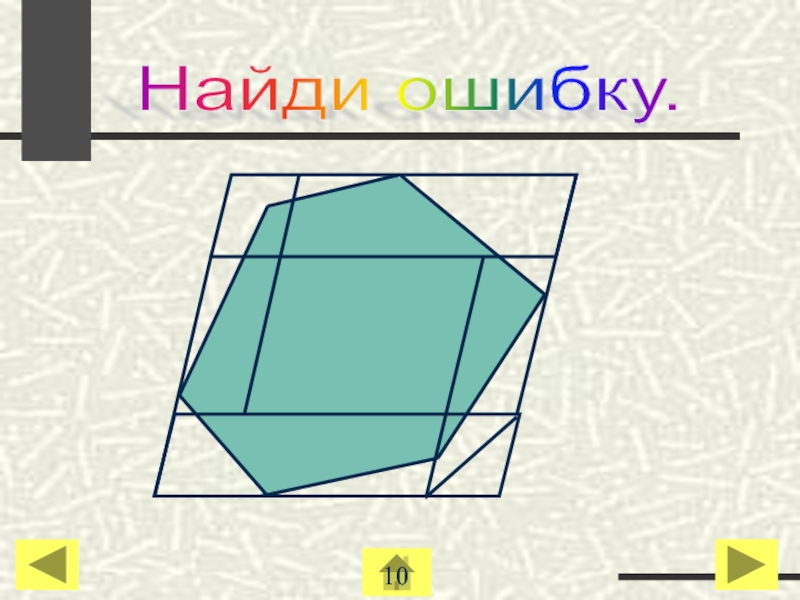
- 56. Найди ошибку. 10
- 57. Найди ошибку. 10
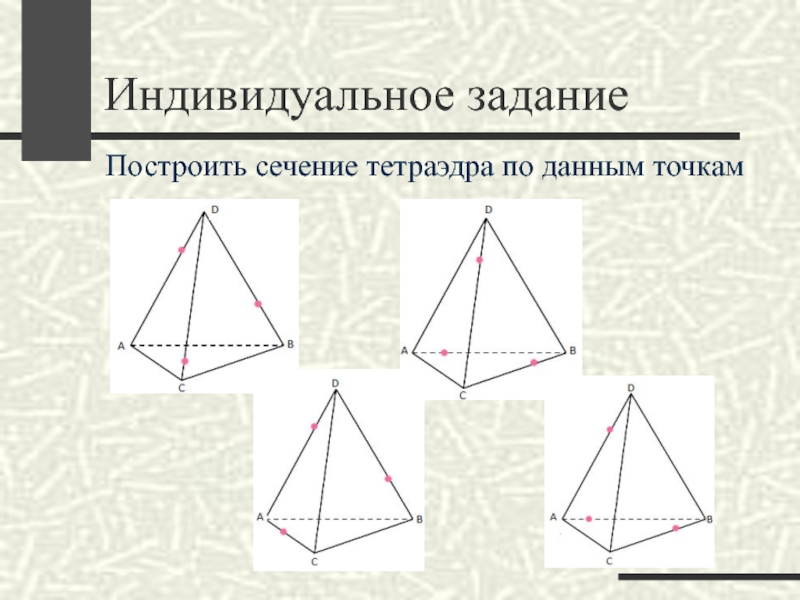
- 58. Индивидуальное задание Построить сечение тетраэдра по данным точкам
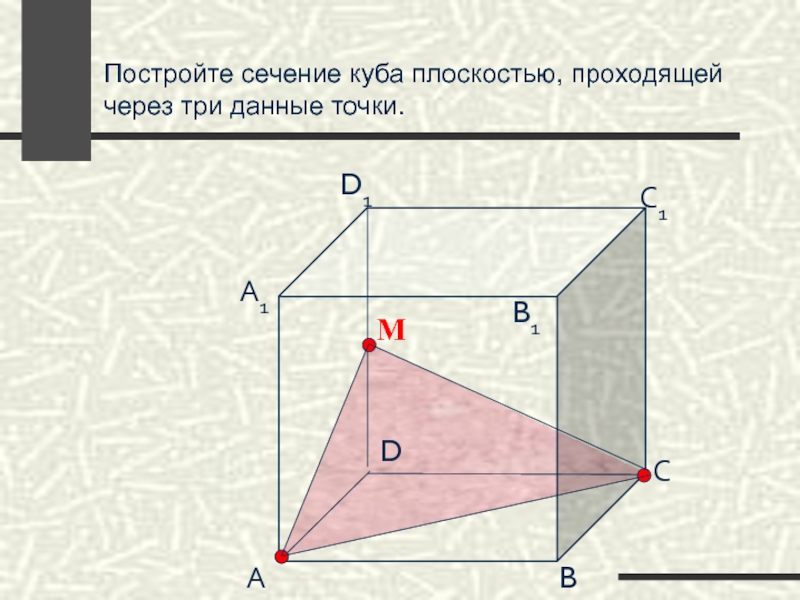
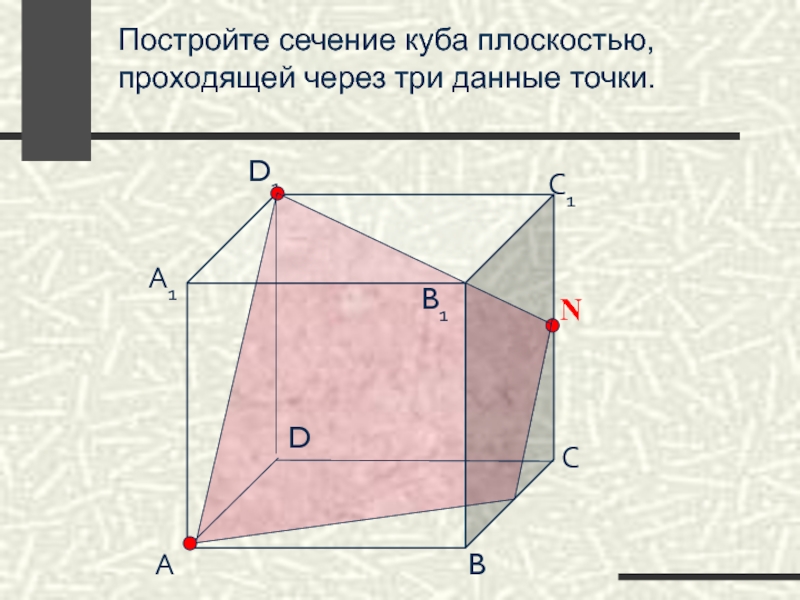
- 59. Постройте сечение куба плоскостью, проходящей через три
- 60. Постройте сечение куба плоскостью, проходящей через три
- 61. Постройте сечение куба плоскостью, проходящей через три
- 62. A B
- 63. Постройте сечение куба плоскостью, проходящей через три
- 64. Постройте сечение куба плоскостью, проходящей через три
- 65. Постройте сечение куба плоскостью, проходящей через три
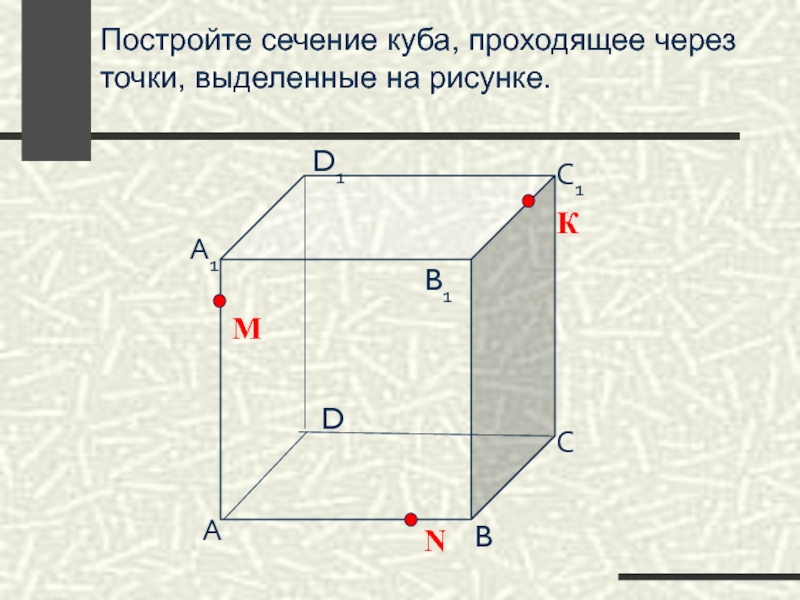
- 66. Постройте сечение куба, проходящее через
- 67. Постойте сечение параллелепипеда плоскостью, проходящей через
- 69. Практическая работа. Постройте сечение многогранника плоскостью, проходящей
- 70. Проверьте правильность построения
- 71. A B C D K
- 72. A B C D K L
- 73. A B C D K L M
- 74. C B A D
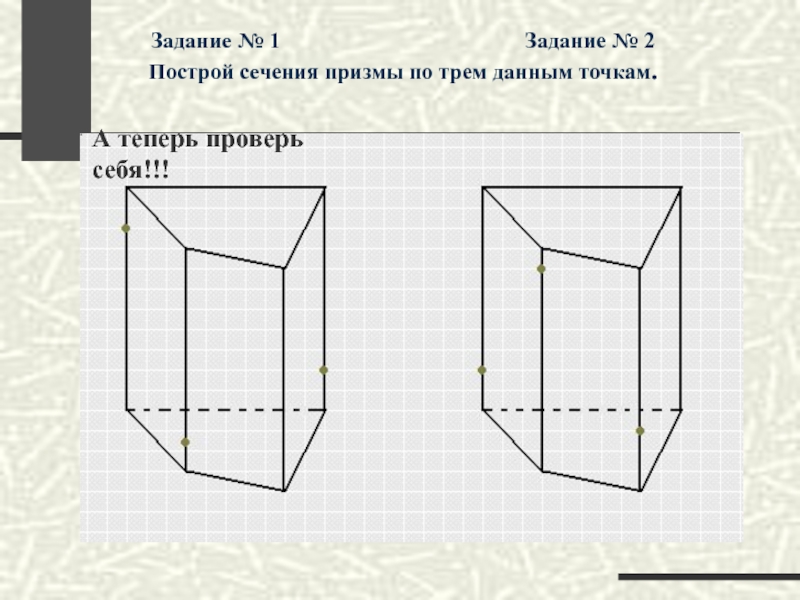
- 75. Задание № 1
- 77. A D C B C1 B1
- 78. А В C D
- 79. Решение задач
- 80. Да, путь познания не гладок. Но знайте
- 81. В тетраэдре ABCD на ребре АВ
- 82. A B C D B1
- 83. A B C D B1
- 84. A B C D B1
- 85. A B C D B1
- 86. A B C D B1
- 87. A B C D C1
- 88. M N K Построить сечение четырехугольной
- 89. Построить сечение
- 90. M N K Рассмотрим теперь более
- 91. Постройте сечение пирамиды плоскостью, проходящей
- 92. XY – след секущей плоскости
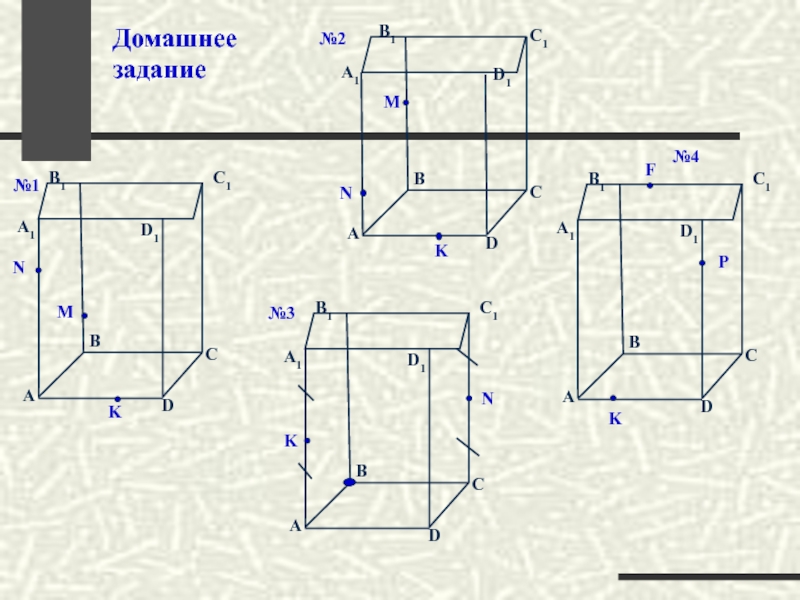
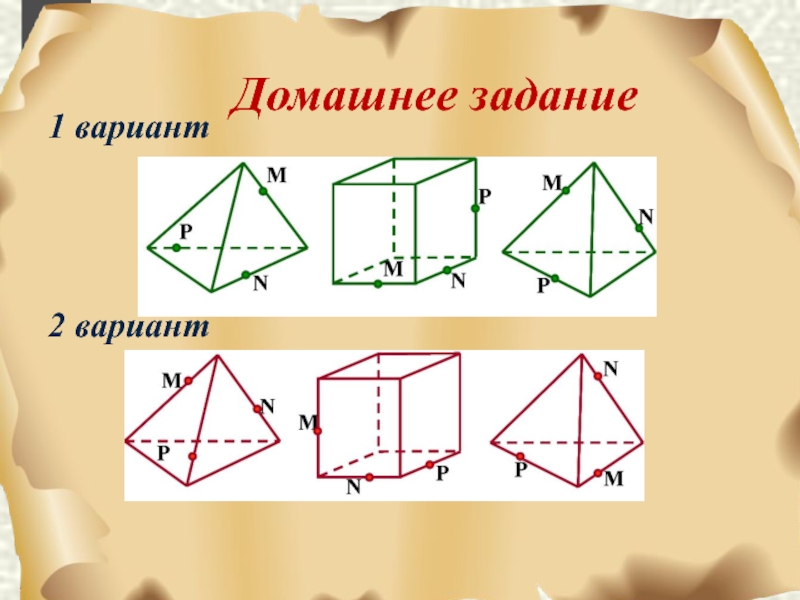
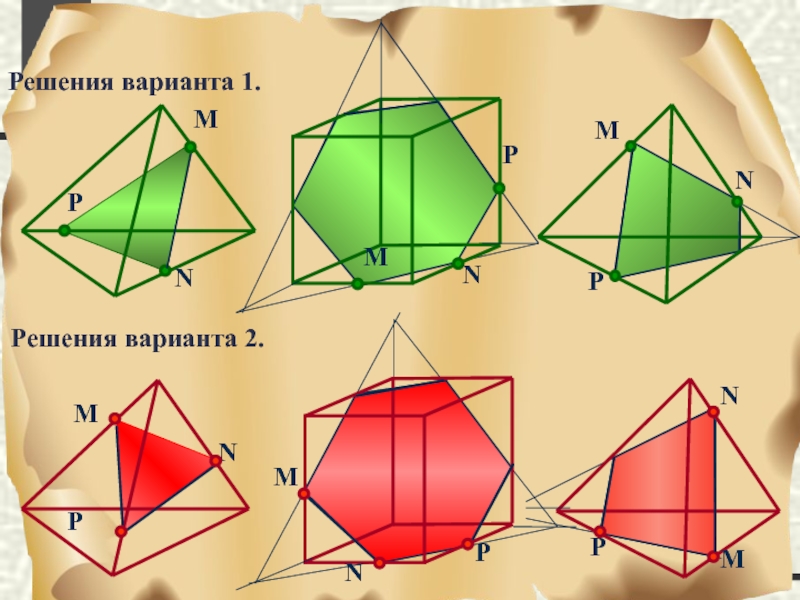
- 93. Домашнее задание 1 вариант 2 вариант
- 94. P N
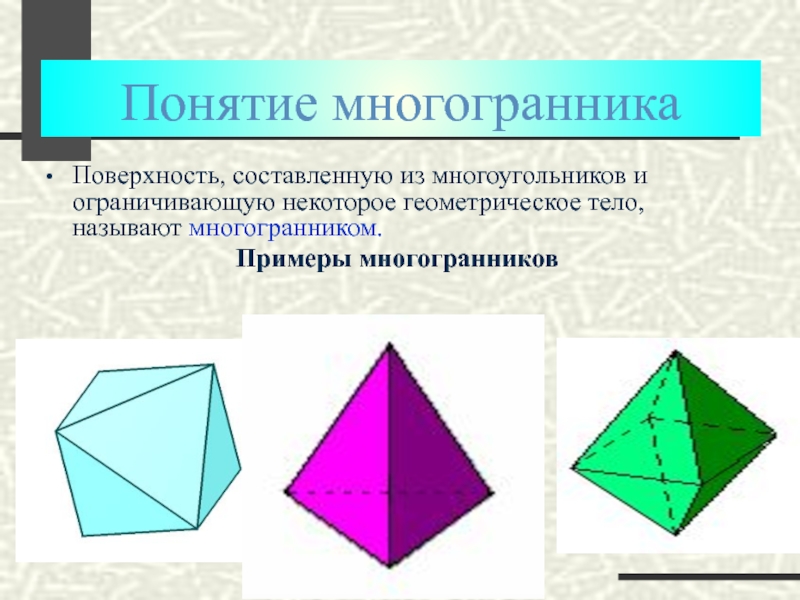
Слайд 3Понятие многогранника
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют
Примеры многогранников
Слайд 8Выпуклый многогранник
Многогранник называется выпуклым, если он расположен по одну сторону от
Все грани выпуклого многогранника являются выпуклыми многоугольниками.
В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360 градусов.
Слайд 9Призма
Призмой называется многогранник, который состоит из двух плоских многоугольников,
лежащих
Слайд 13Гексаэдр
Куб составлен из шести квадратов. Каждая его вершина является вершиной трех
Сумма плоских углов при каждой вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер
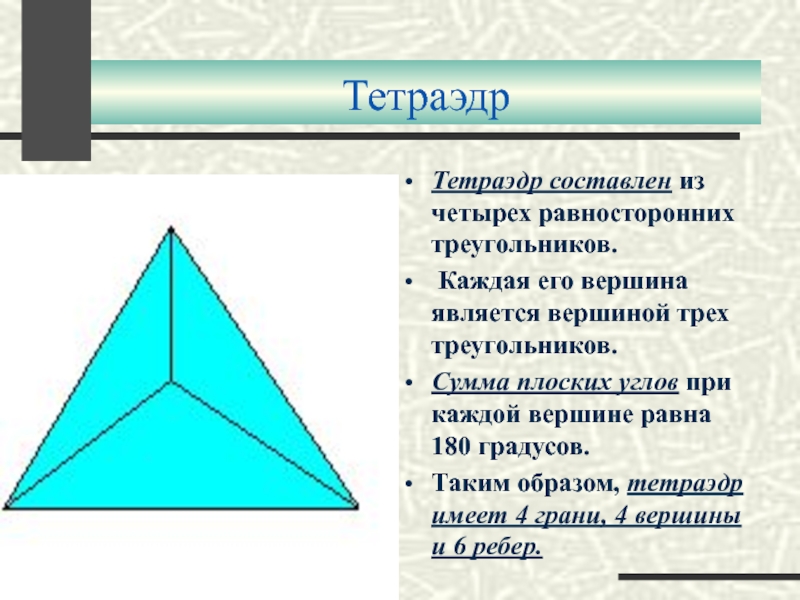
Слайд 14Тетраэдр
Тетраэдр составлен из четырех равносторонних треугольников.
Каждая его вершина является вершиной
Сумма плоских углов при каждой вершине равна 180 градусов.
Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Слайд 15Октаэдр
Октаэдр составлен из восьми равносторонних треугольников.
Каждая его вершина является вершиной
Сумма углов при плоских каждой вершине равна 240 градусов.
Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
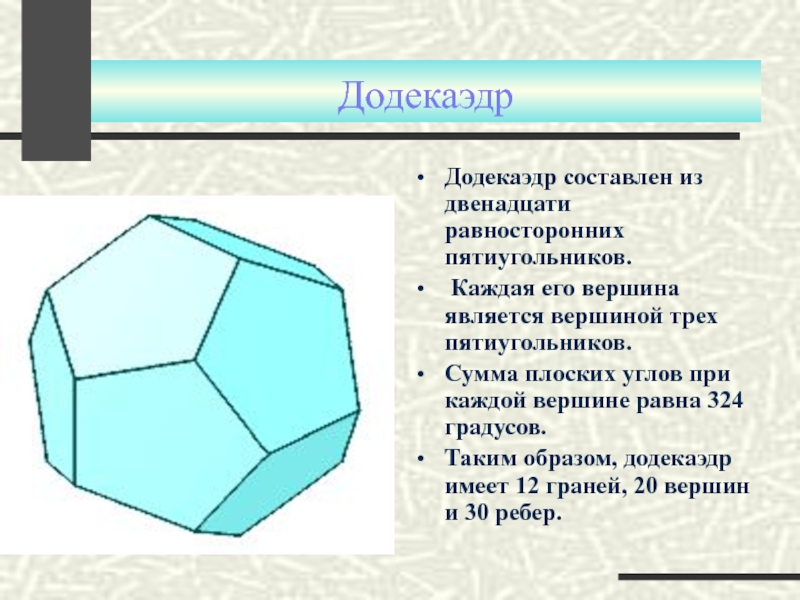
Слайд 16Додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников.
Каждая его вершина является вершиной
Сумма плоских углов при каждой вершине равна 324 градусов.
Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
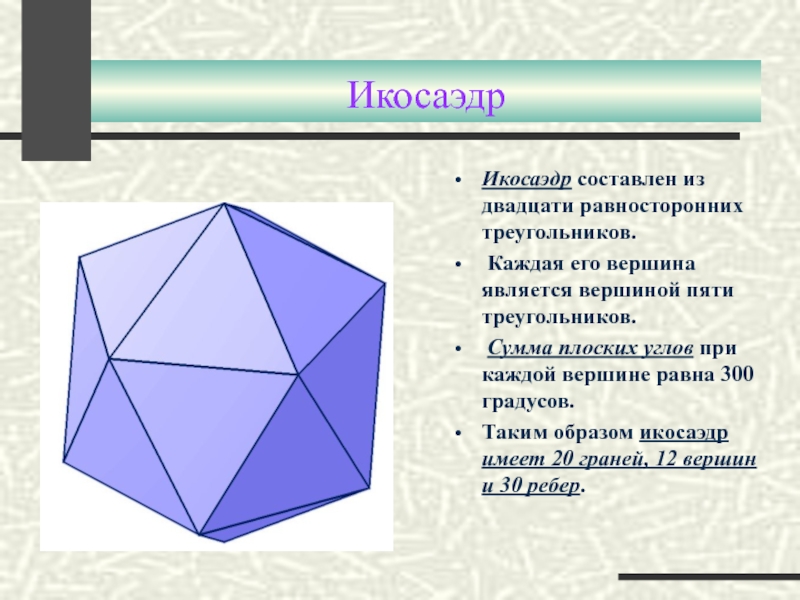
Слайд 17Икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников.
Каждая его вершина является вершиной
Сумма плоских углов при каждой вершине равна 300 градусов.
Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
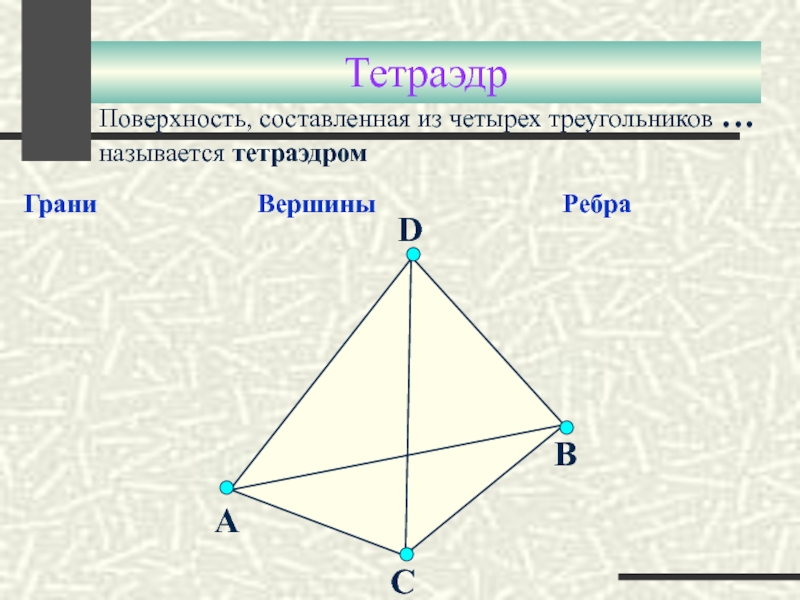
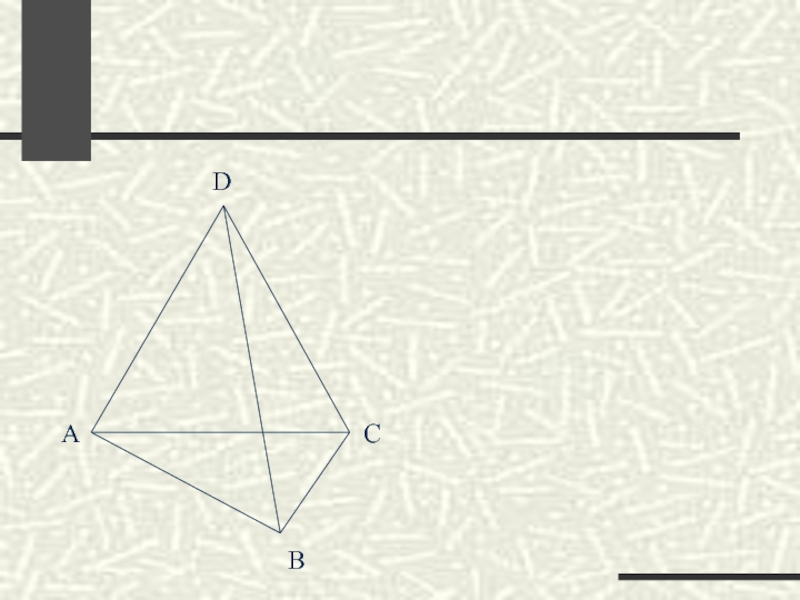
Слайд 18
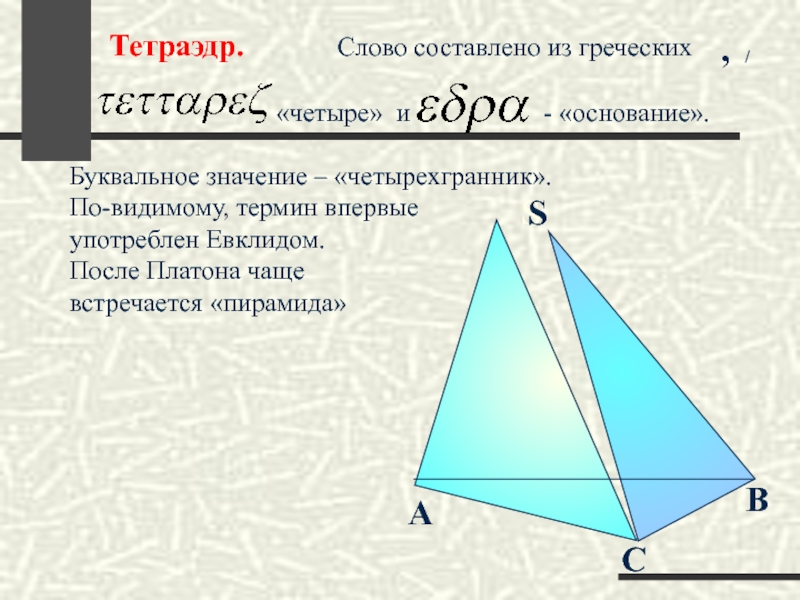
D
А
С
В
Поверхность, составленная из четырех треугольников …
называется тетраэдром
Грани
Тетраэдр
Слайд 22Тетраэдр
C
A
D
B
Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани
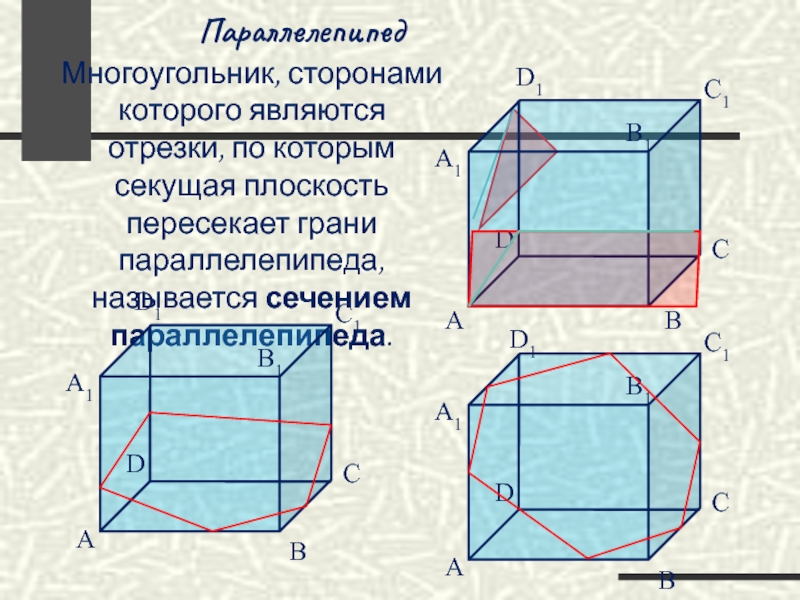
Слайд 23Параллелепипед
Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани
D1
Слайд 24
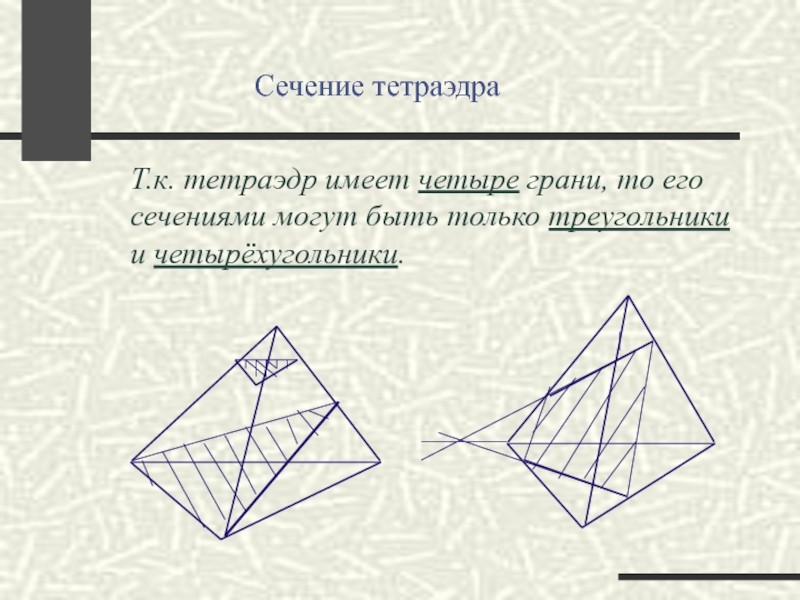
Сечение
Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
Слайд 25 Правила построения сечений ТЕТРАЭДРА
а)Проводим прямые через точки, лежащие в одной
б) Ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:
-- ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
-- параллельные грани плоскость сечения пересекает по параллельным прямым.
Слайд 26А
B
D
C
N
M
K
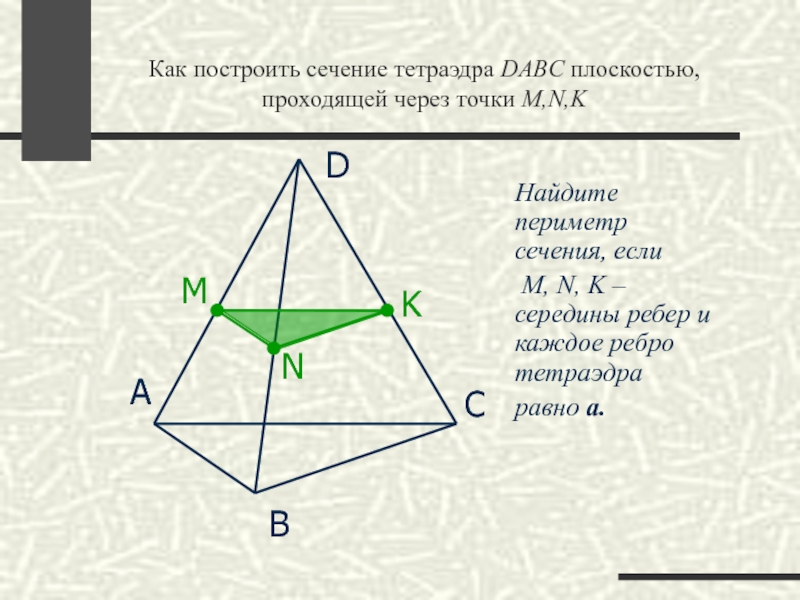
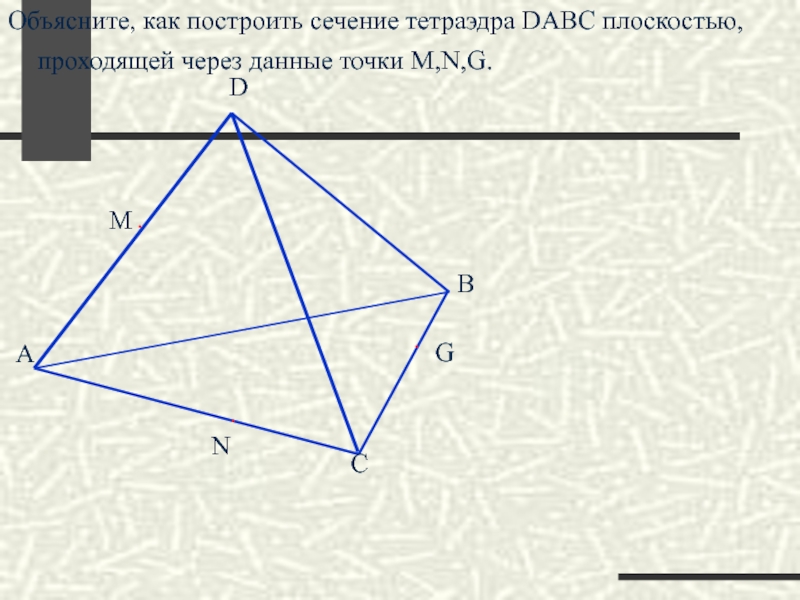
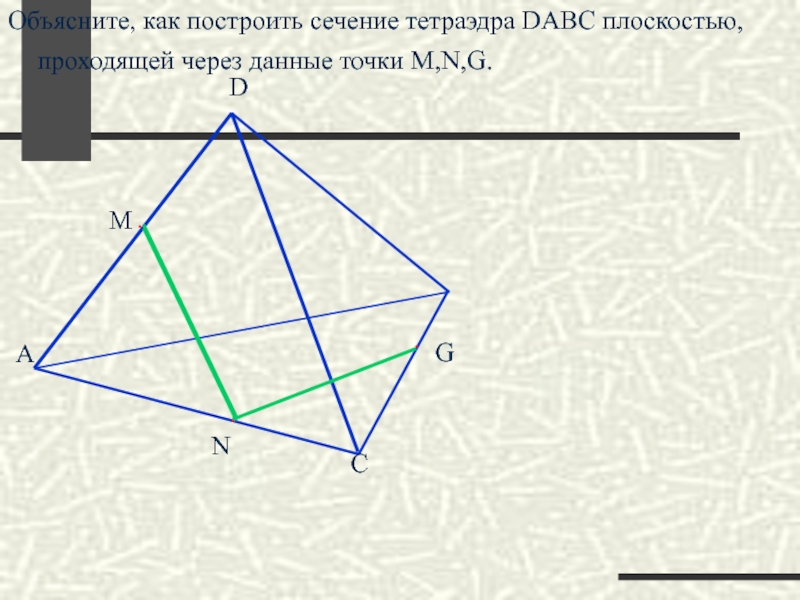
Как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K
Найдите периметр
M, N, K – середины ребер и каждое ребро тетраэдра
равно а.
Слайд 27А
B
D
C
N
M
K
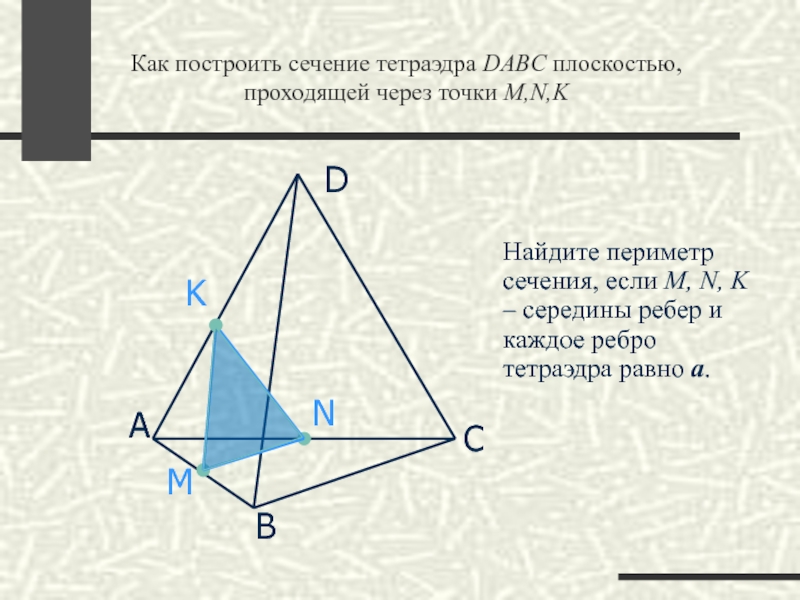
Как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K
Найдите периметр
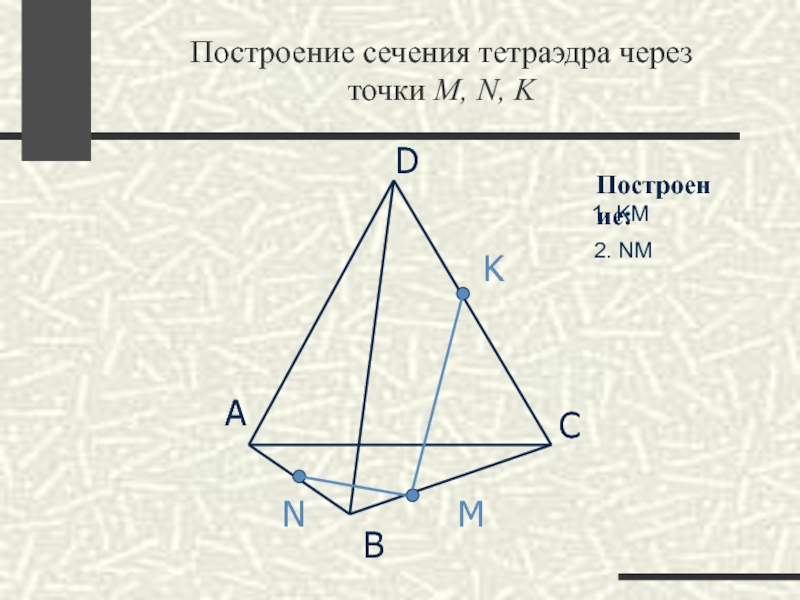
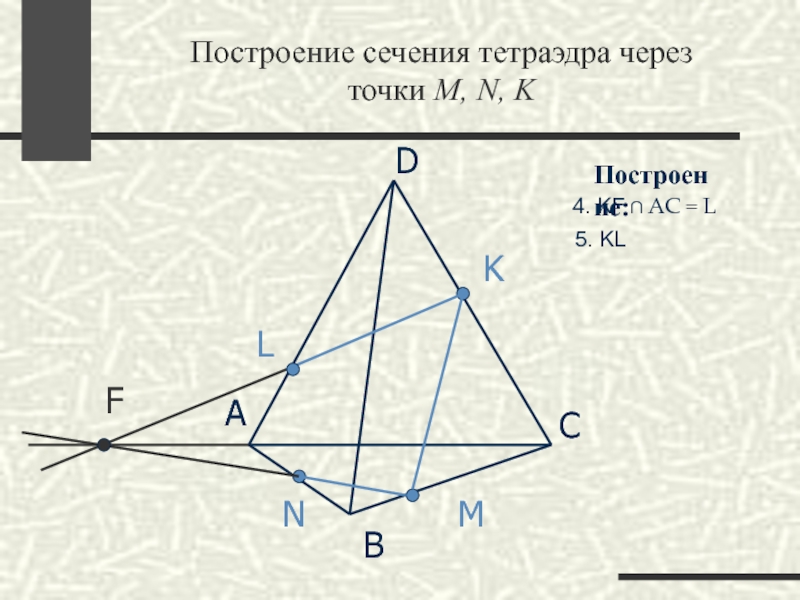
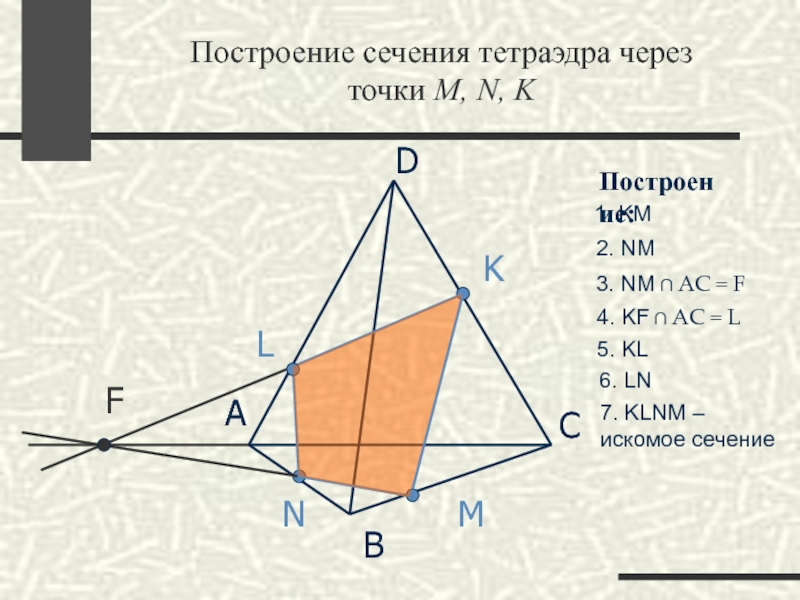
Слайд 31Построение сечения тетраэдра через
точки M, N, K
А
B
D
C
N
M
K
L
F
Построение:
1. KM
2. NM
3. NM
4. KF ∩ АС = L
5. KL
6. LN
7. KLNM – искомое сечение
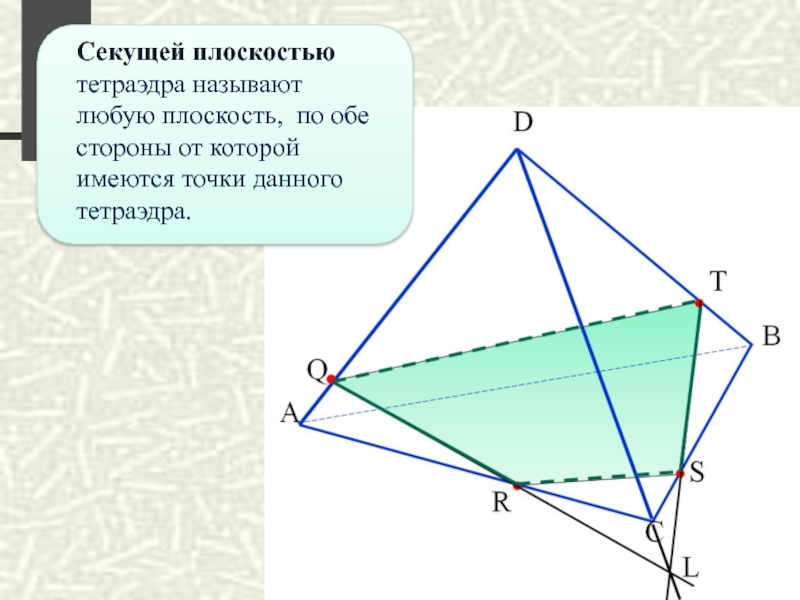
Слайд 32
Секущей плоскостью тетраэдра называют любую плоскость, по обе стороны от которой
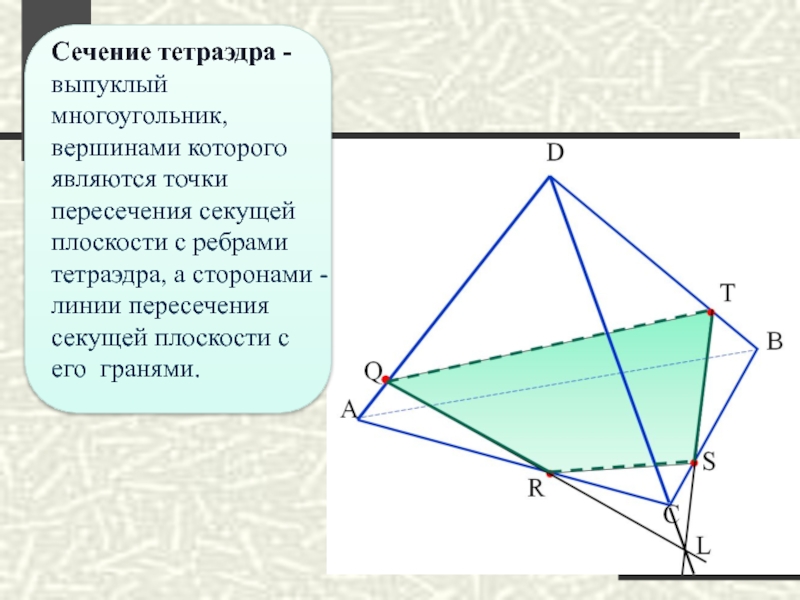
Слайд 33
Сечение тетраэдра - выпуклый многоугольник, вершинами которого являются точки пересечения секущей
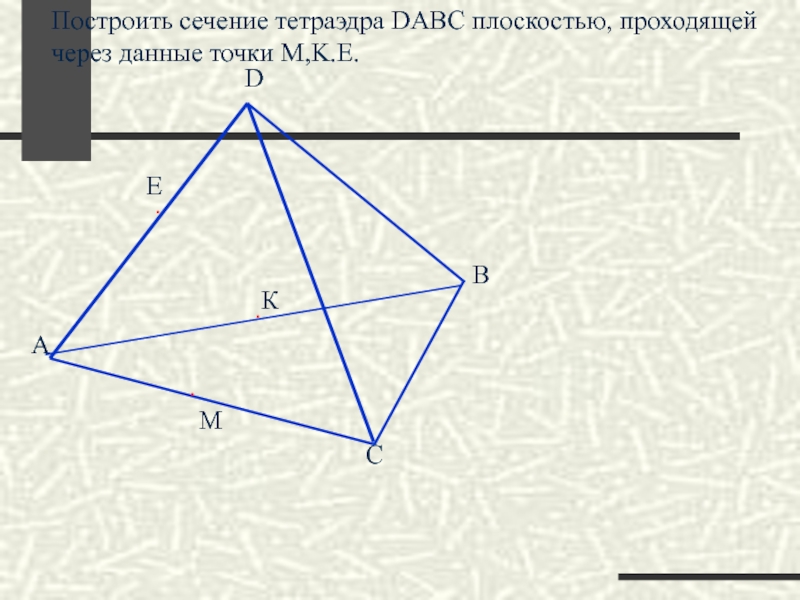
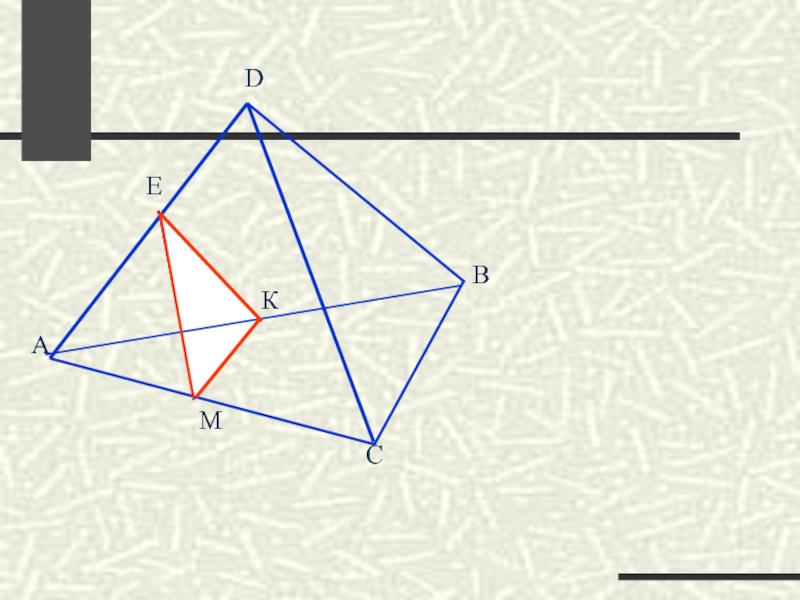
Слайд 34Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M,K.E.
А
D
B
C
Е
М
К
∙
∙
∙
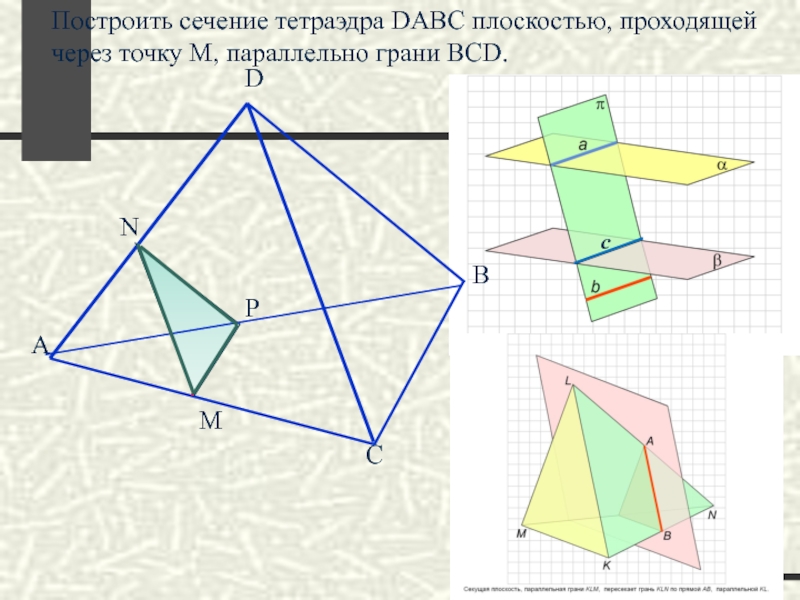
Слайд 36
Построить сечение тетраэдра DABC плоскостью, проходящей через точку M, параллельно грани
А
D
B
C
М
∙
N
P
Слайд 37
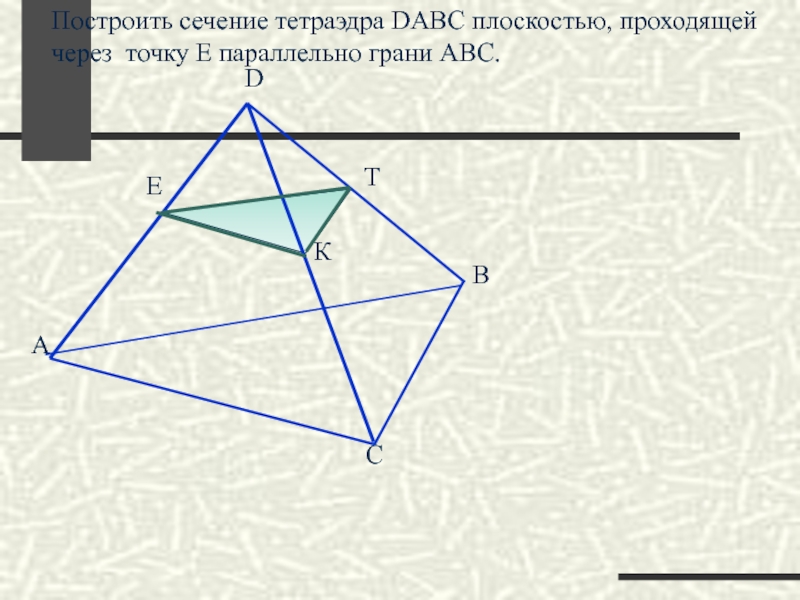
Построить сечение тетраэдра DABC плоскостью, проходящей через точку Е параллельно грани
А
D
B
C
Е
∙
К
Т
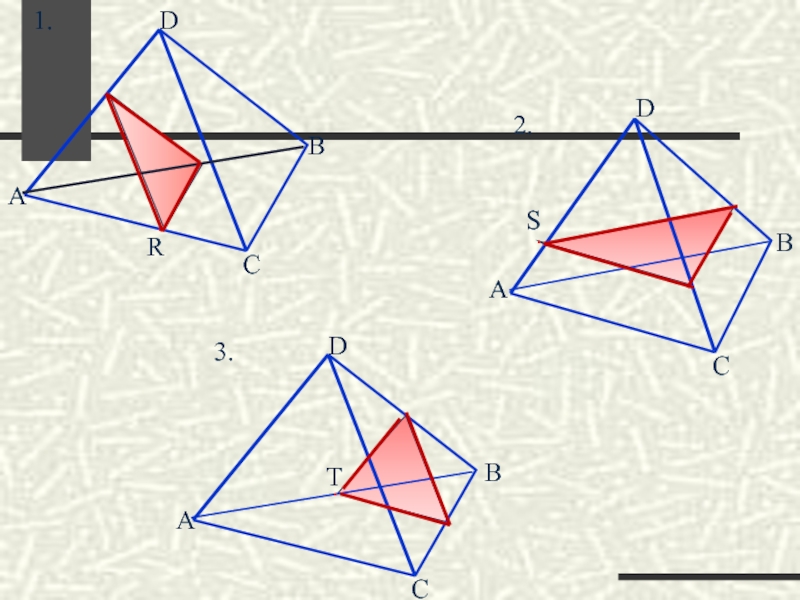
Слайд 38Задание
Построить сечение тетраэдра ABCD, проходящее через точку R параллельно грани BCD.
Построить
Построить сечение тетраэдра ABCD, проходящее через точку T параллельно грани ACD.
Слайд 45
А
С
В
D
N
P
Q
R
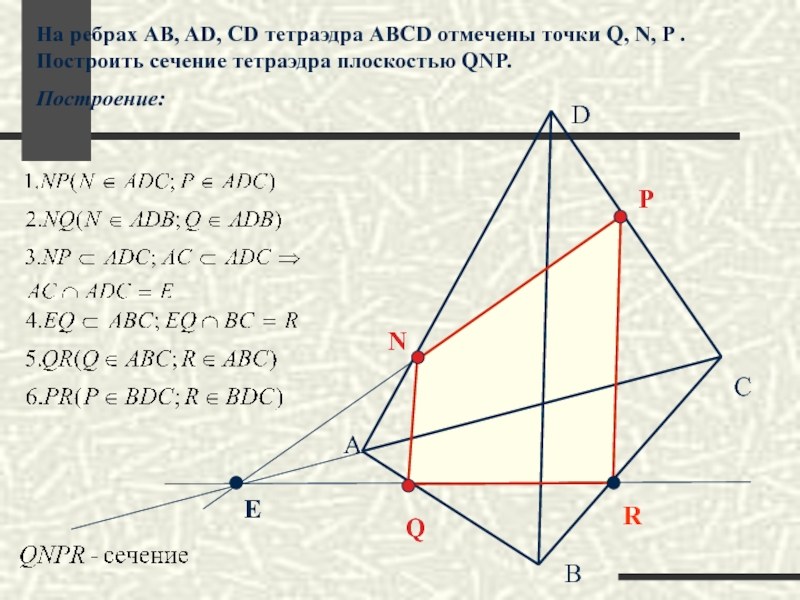
На ребрах AB, AD, CD тетраэдра ABCD отмечены точки Q, N,
Построение:
E
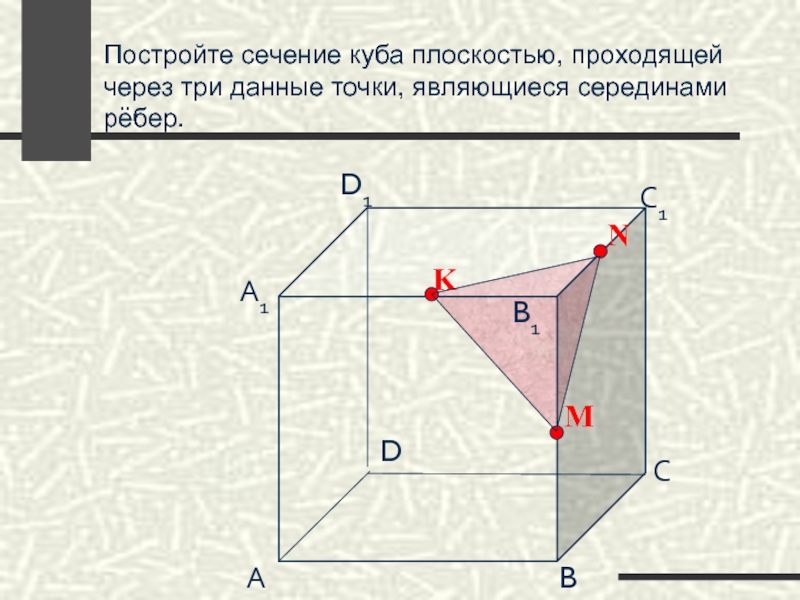
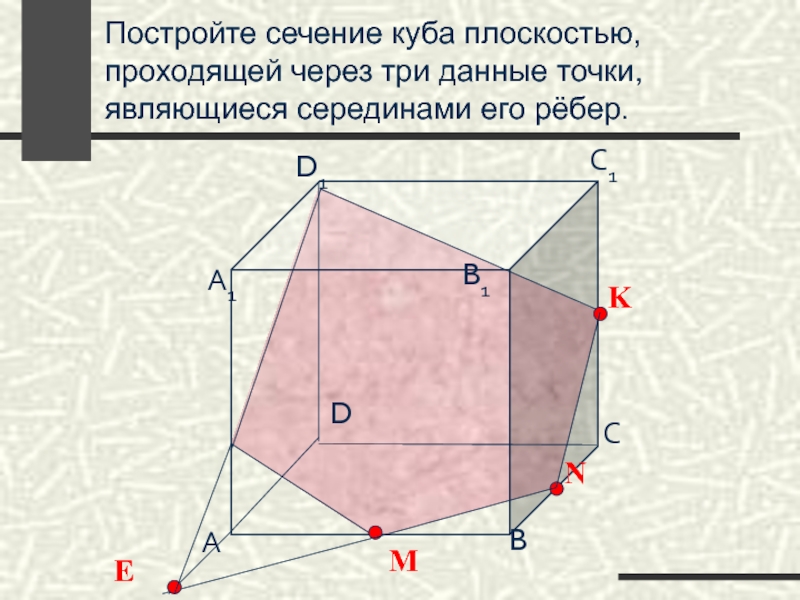
Слайд 59Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами
А
B
С
D
D1
С1
B1
А1
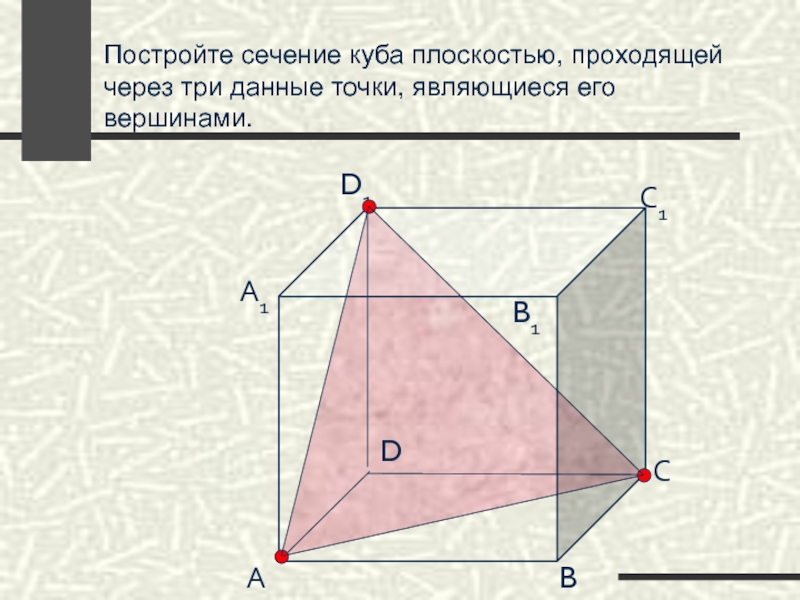
Слайд 60Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся его
А
B
С
D
D1
С1
B1
А1
Слайд 62
A
B
С
B1
D1
D
K
M
C1
A1
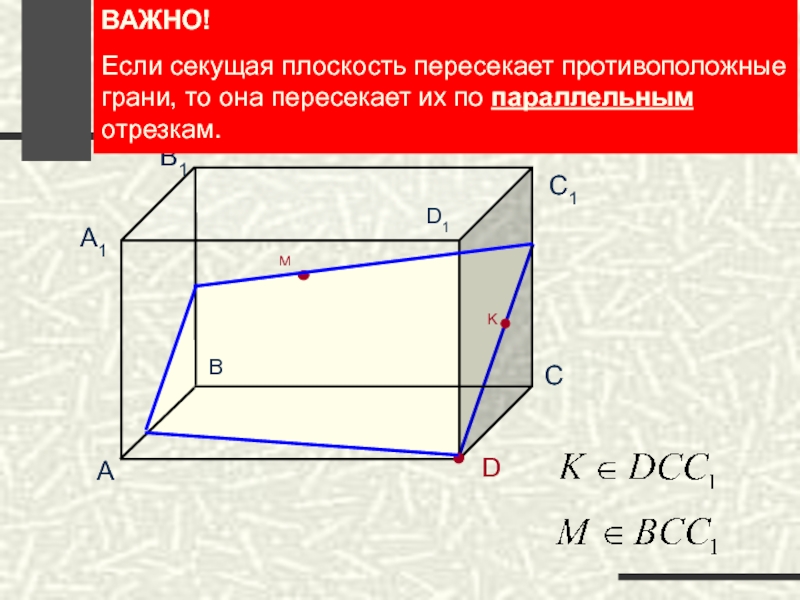
ВАЖНО!
Если секущая плоскость пересекает противоположные грани, то она пересекает их по
Слайд 64Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами
А
B
С
D
D1
С1
B1
А1
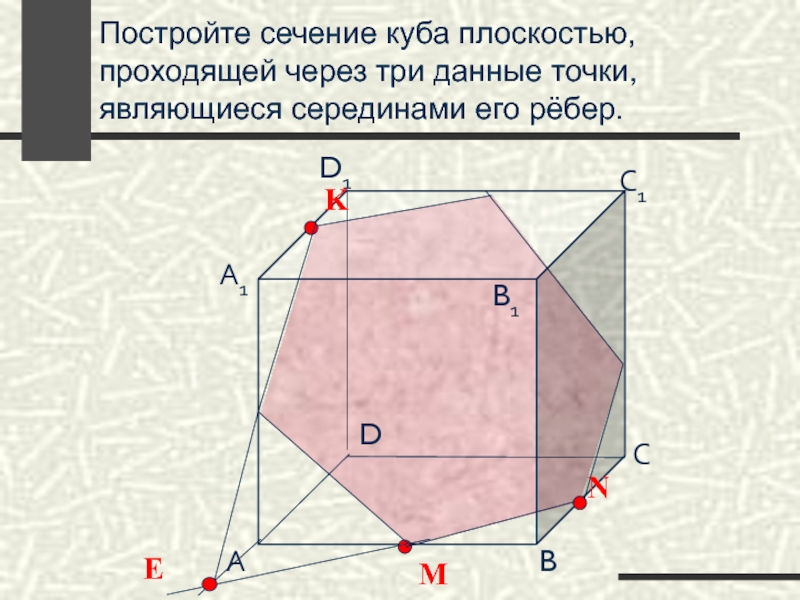
Слайд 65Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами
А
B
С
D
D1
С1
B1
А1
Слайд 67
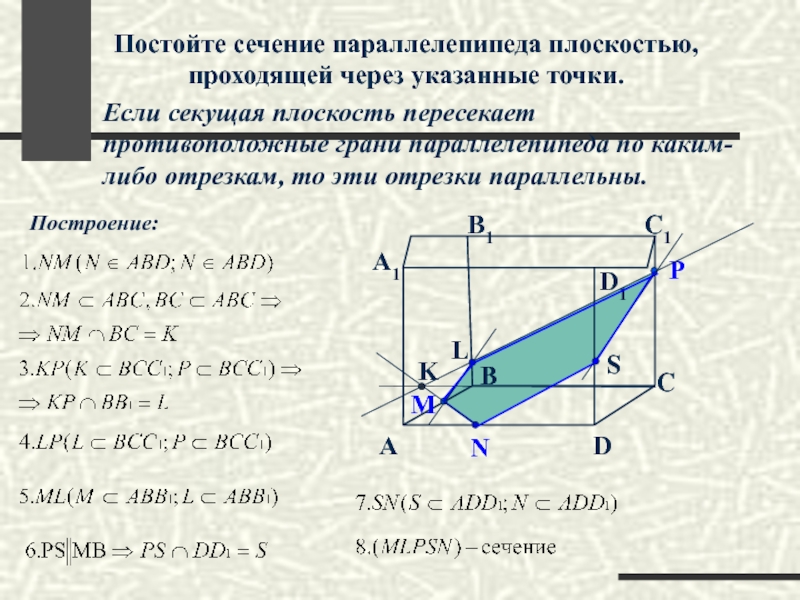
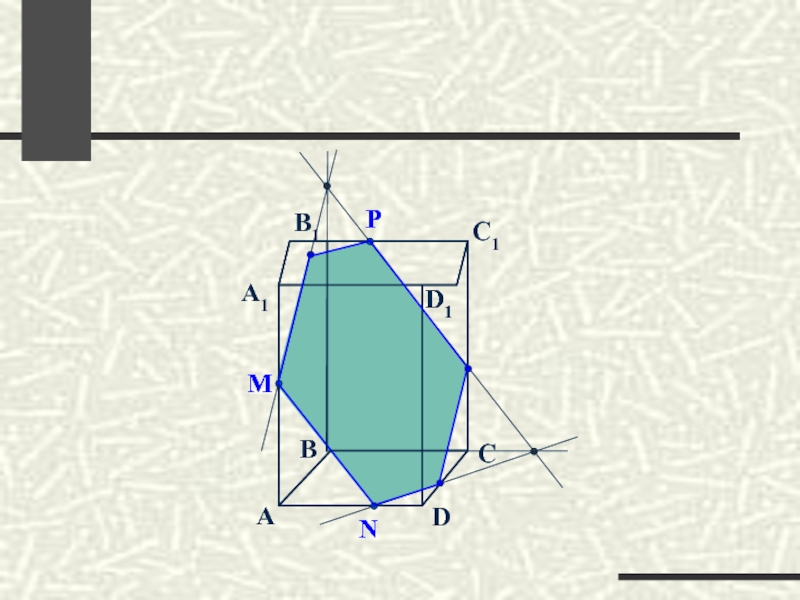
Постойте сечение параллелепипеда плоскостью, проходящей через указанные точки.
Если секущая плоскость пересекает
S
L
K
Построение:
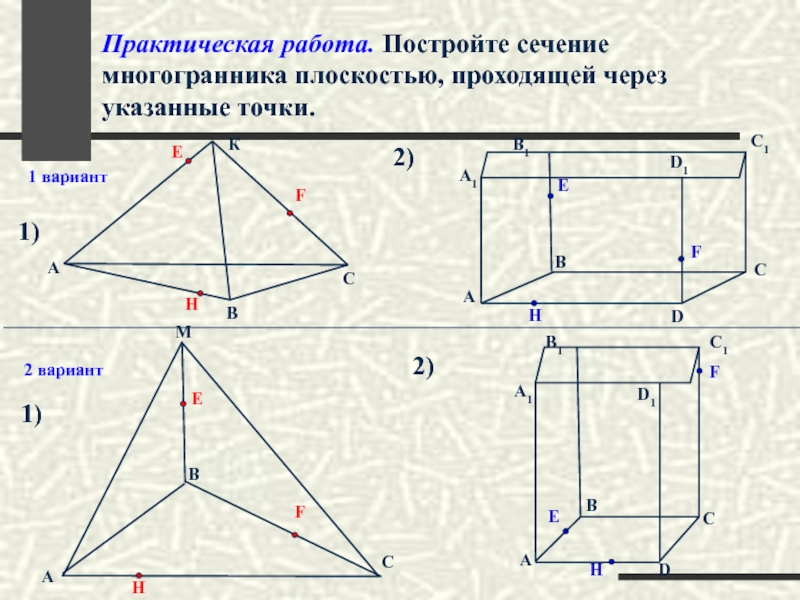
Слайд 69Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки.
M
A
А1
1)
1)
2)
2)
В
С
К
В
A
С
A
D
C
B
A
В
С
D
B1
С1
D1
C1
B1
A1
D1
E
F
H
E
H
F
H
E
F
F
H
E
1 вариант
2
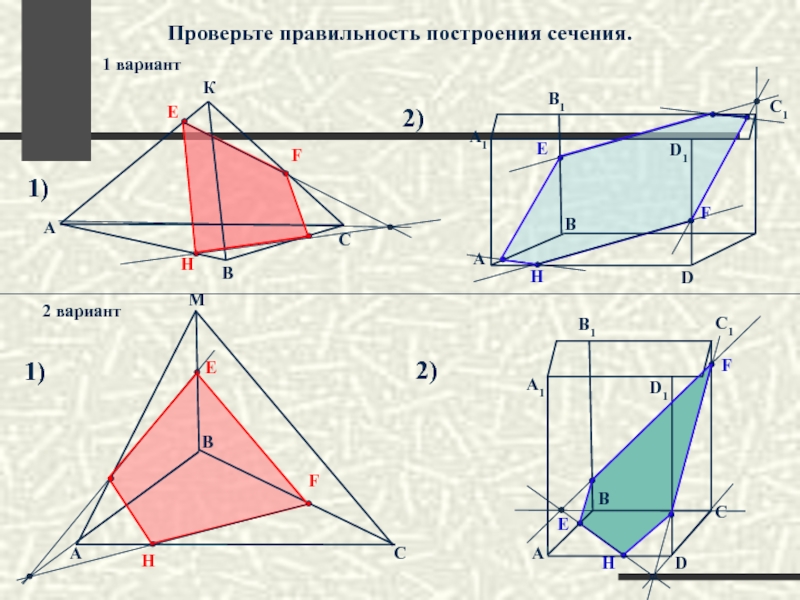
Слайд 70
Проверьте правильность построения сечения.
M
A
А1
1)
2)
В
С
К
В
A
С
A
D
C
B
A
В
D
B1
С1
D1
C1
B1
A1
D1
E
F
H
E
H
F
H
E
F
F
H
E
1 вариант
2 вариант
1)
2)
Слайд 71
A
B
C
D
K
L
M
N
F
G
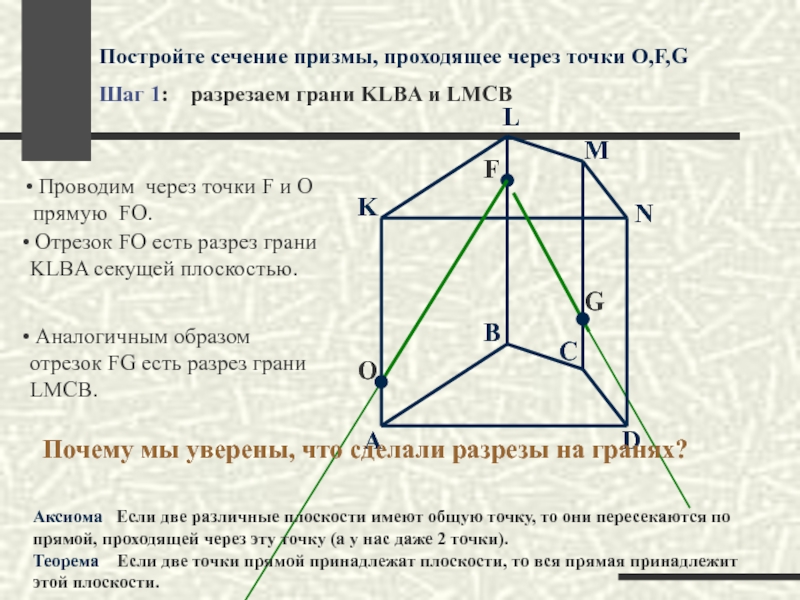
Проводим через точки F и O прямую FO.
O
Отрезок FO есть разрез грани KLBA секущей плоскостью.
Аналогичным образом отрезок FG есть разрез грани LMCB.
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Почему мы уверены, что сделали разрезы на гранях?
Постройте сечение призмы, проходящее через точки O,F,G
Шаг 1: разрезаем грани KLBA и LMCB
Слайд 72A
B
C
D
K
L
M
N
F
G
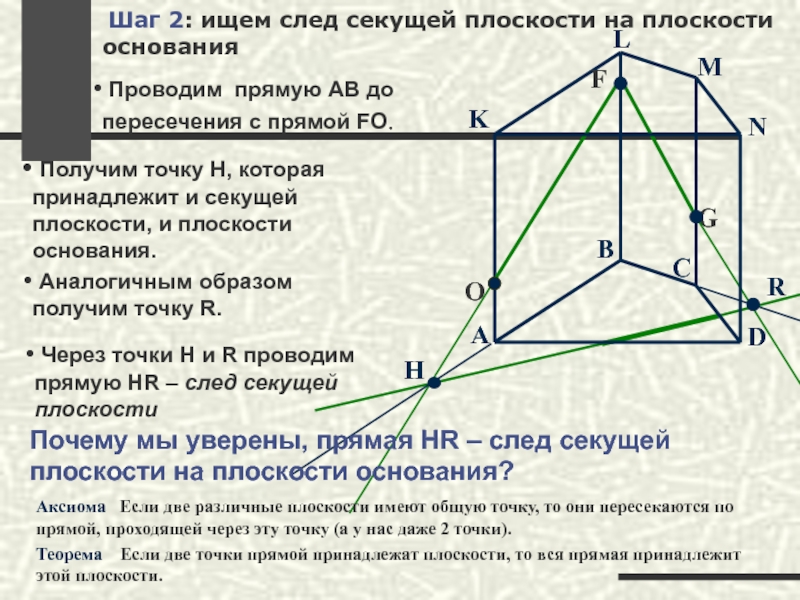
Шаг 2: ищем след секущей плоскости на плоскости основания
Проводим
O
Получим точку H, которая принадлежит и секущей плоскости, и плоскости основания.
Аналогичным образом получим точку R.
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Через точки H и R проводим прямую HR – след секущей плоскости
Почему мы уверены, прямая HR – след секущей плоскости на плоскости основания?
Слайд 73A
B
C
D
K
L
M
N
F
G
O
E
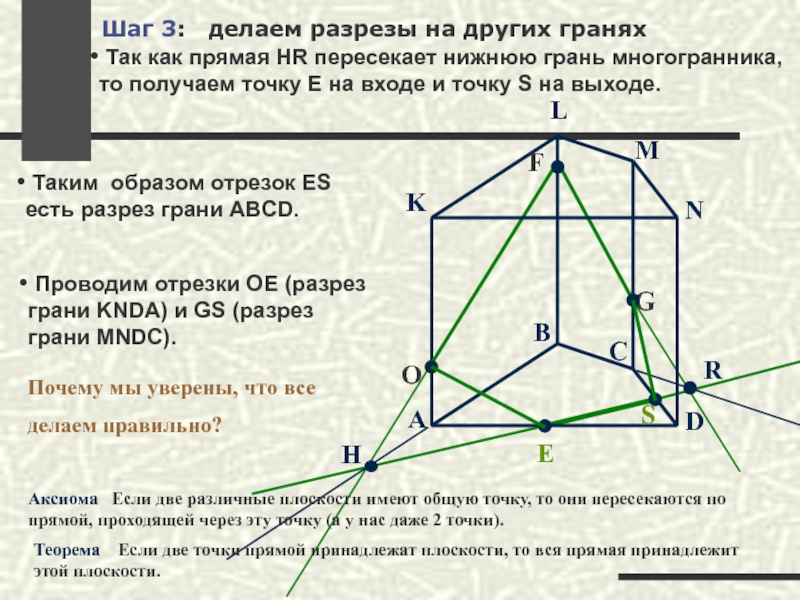
Шаг 3: делаем разрезы на других гранях
Так как прямая
S
Таким образом отрезок ES есть разрез грани ABCD.
Проводим отрезки ОЕ (разрез грани KNDA) и GS (разрез грани MNDC).
Почему мы уверены, что все
делаем правильно?
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Слайд 74C
B
A
D
K
L
M
N
F
G
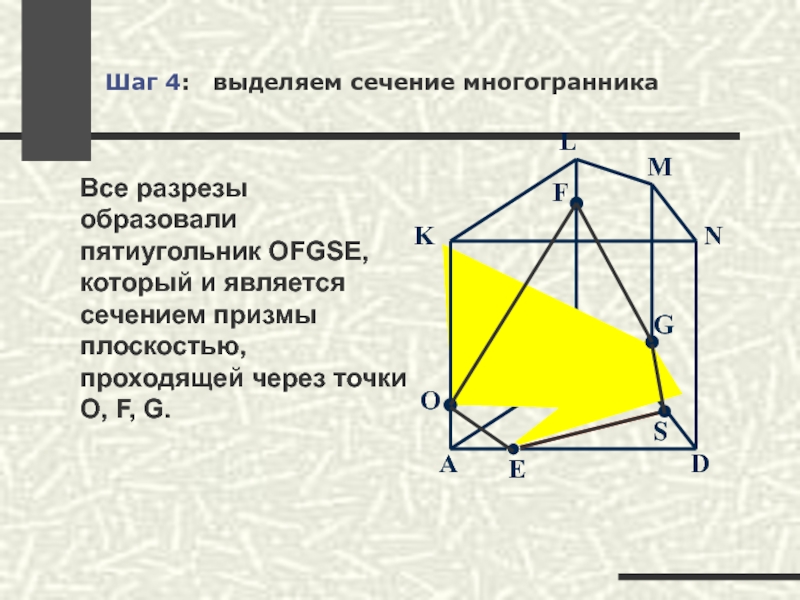
Шаг 4: выделяем сечение многогранника
Все разрезы образовали пятиугольник OFGSE, который
O
Слайд 75Задание № 1
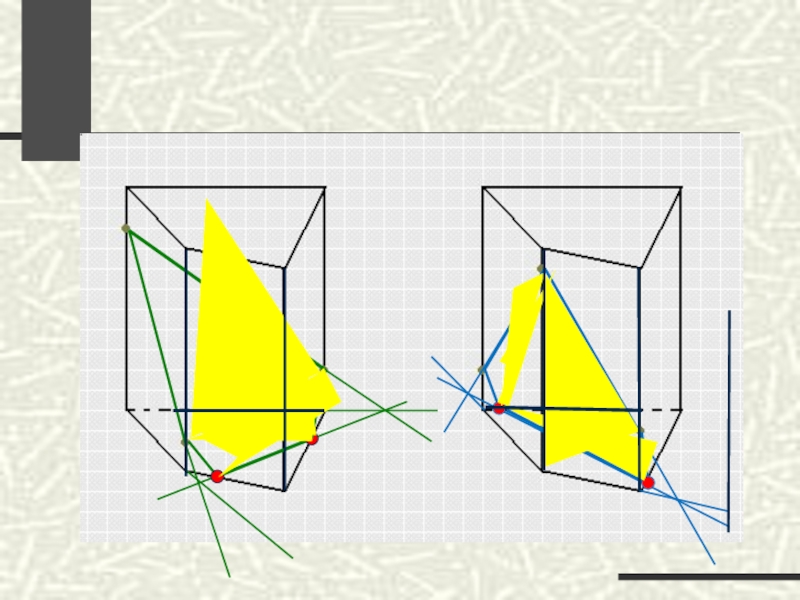
А теперь проверь себя!!!
Слайд 80Да, путь познания не гладок.
Но знайте вы со школьных лет:
Загадок больше,
И поискам предела нет.
Слайд 81
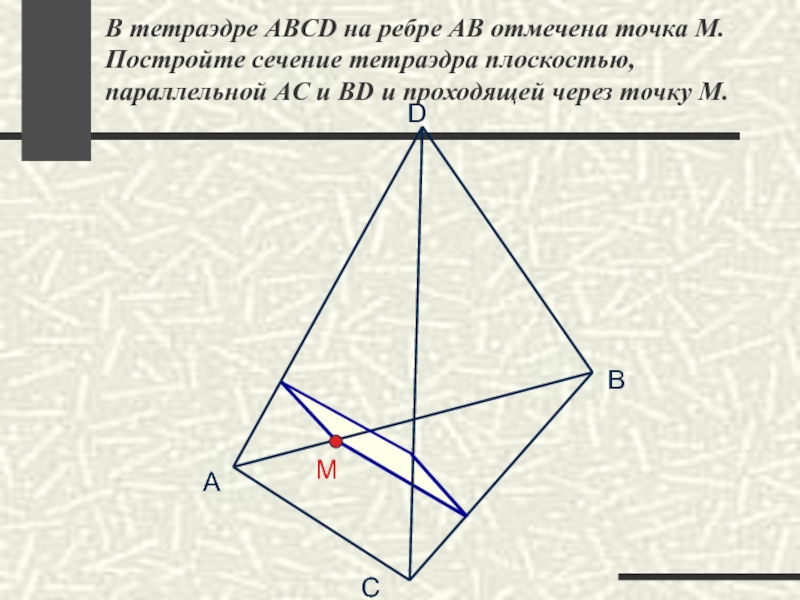
В тетраэдре ABCD на ребре АВ отмечена точка М. Постройте сечение
A
B
C
D
M
Слайд 82
A
B
C
D
B1
C1
D1
M
N
K
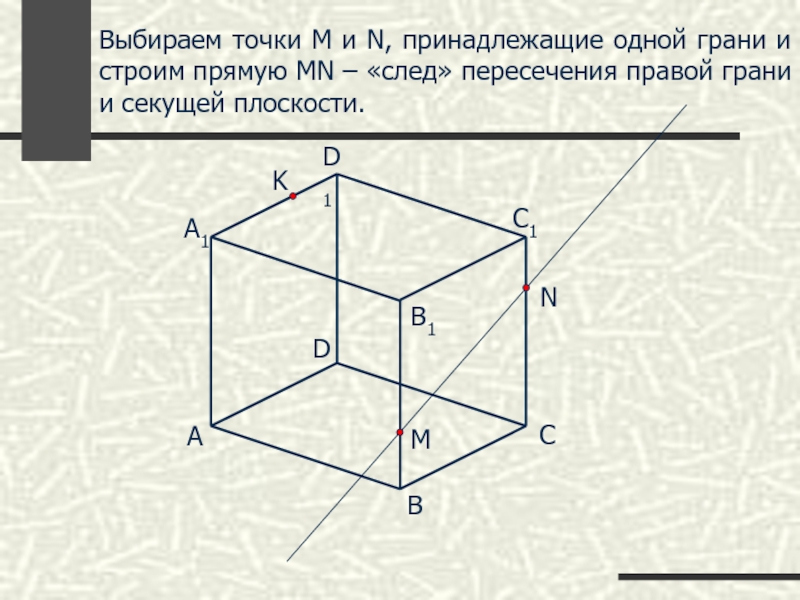
Выбираем точки М и N, принадлежащие одной грани и строим прямую
A1
Слайд 83
A
B
C
D
B1
C1
D1
M
N
K
A1
E
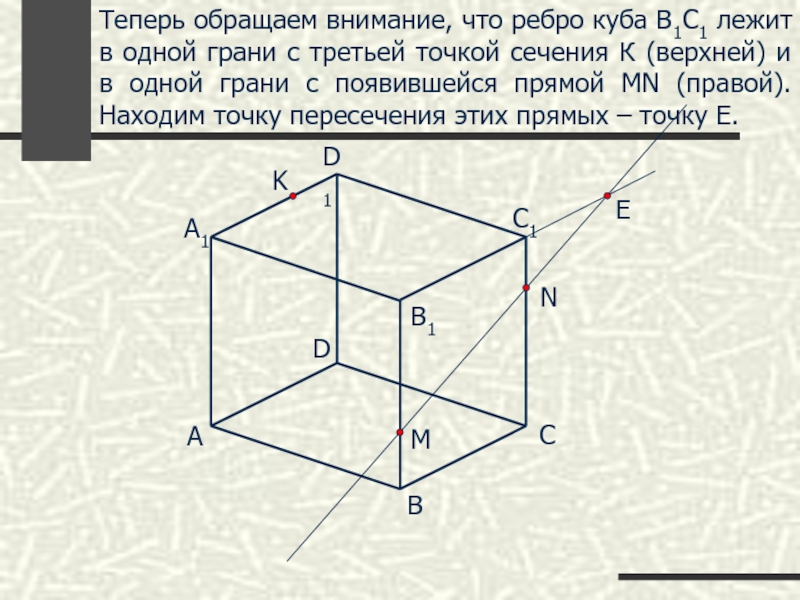
Теперь обращаем внимание, что ребро куба В1С1 лежит в одной грани
Слайд 84
A
B
C
D
B1
C1
D1
M
N
K
A1
E
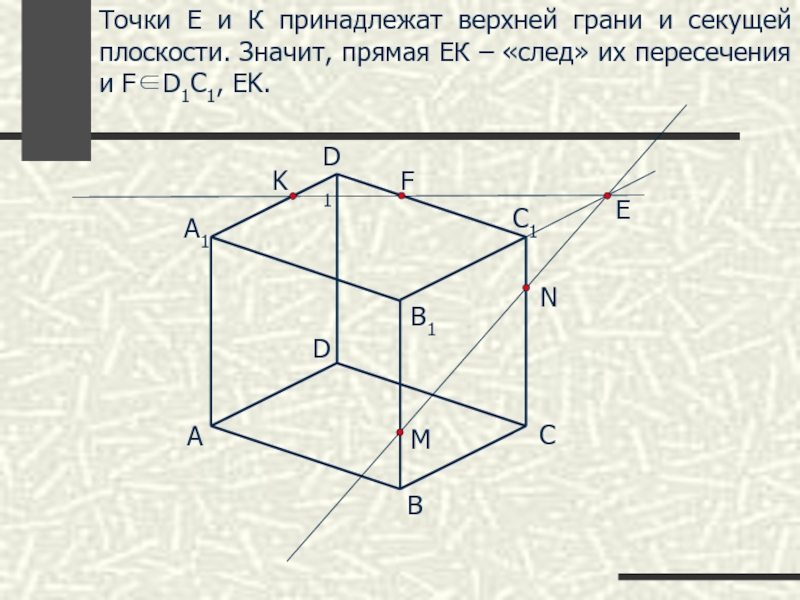
Точки Е и К принадлежат верхней грани и секущей плоскости. Значит,
F
Слайд 85
A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
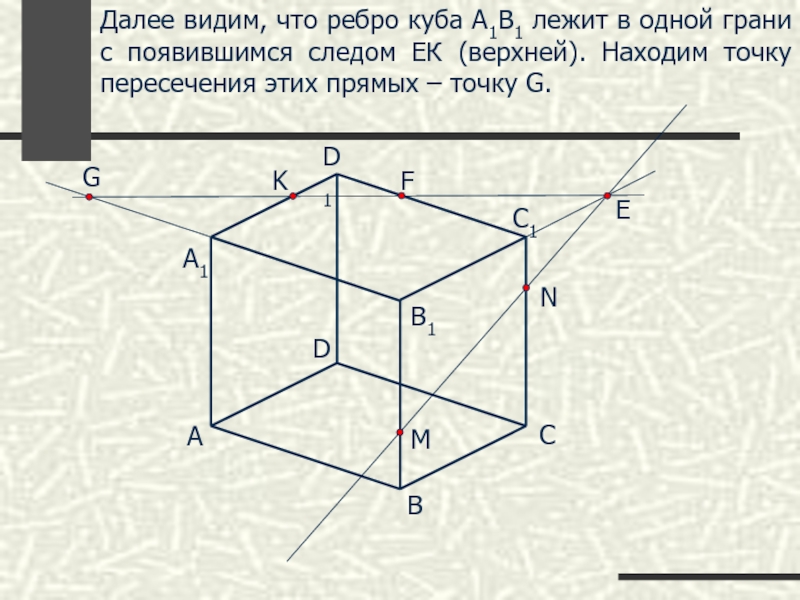
Далее видим, что ребро куба А1В1 лежит в одной грани с
G
Слайд 86
A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
G
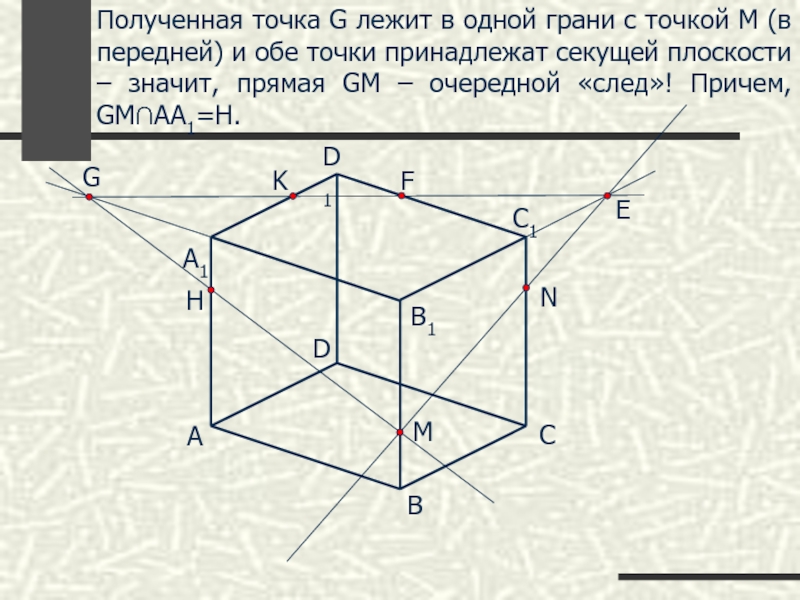
Полученная точка G лежит в одной грани с точкой М (в
H
Слайд 87
A
B
C
D
C1
D1
M
N
K
A1
E
F
G
H
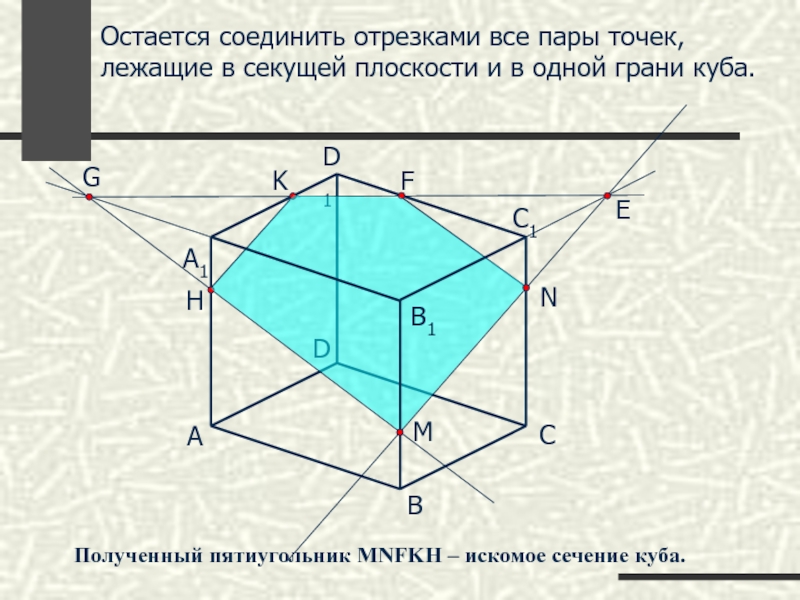
Остается соединить отрезками все пары точек, лежащие в секущей плоскости и
Полученный пятиугольник MNFKH – искомое сечение куба.
B1
Слайд 88
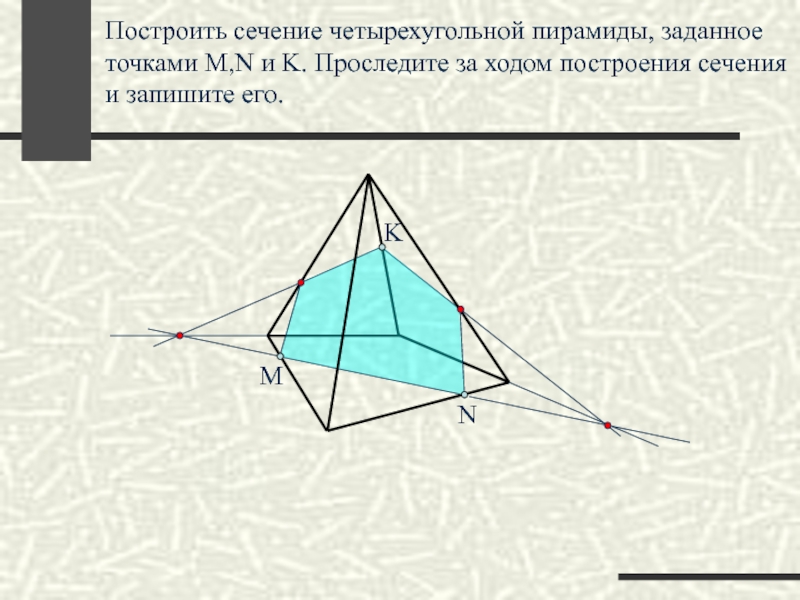
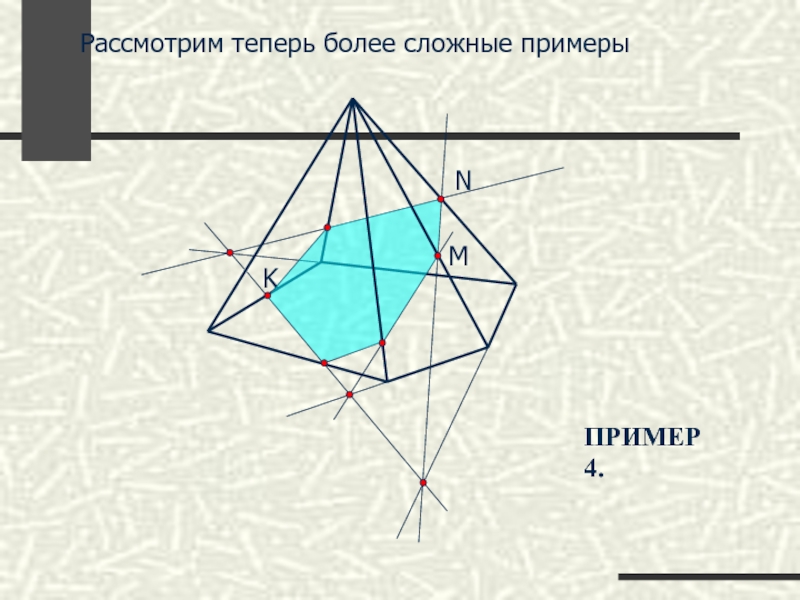
M
N
K
Построить сечение четырехугольной пирамиды, заданное точками M,N и K. Проследите за
Слайд 89
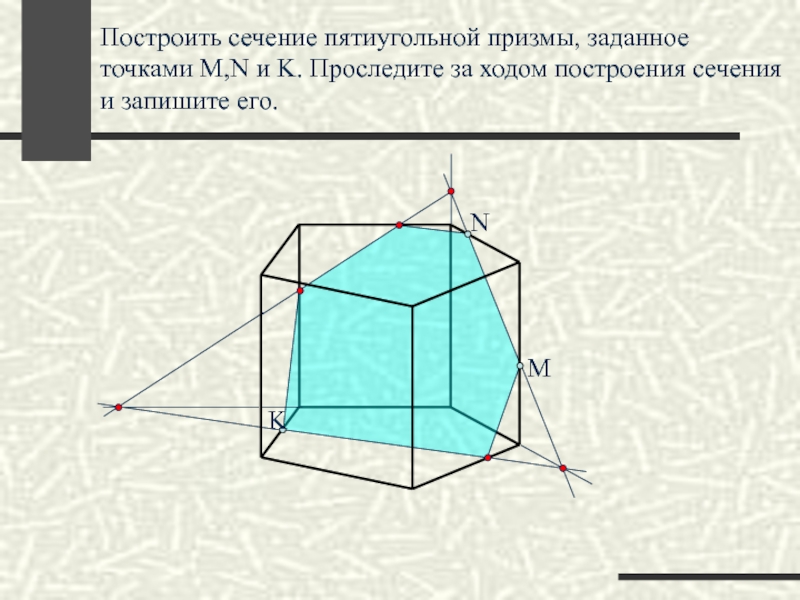
Построить сечение пятиугольной призмы, заданное точками M,N и K. Проследите за
M
N
K
Слайд 91
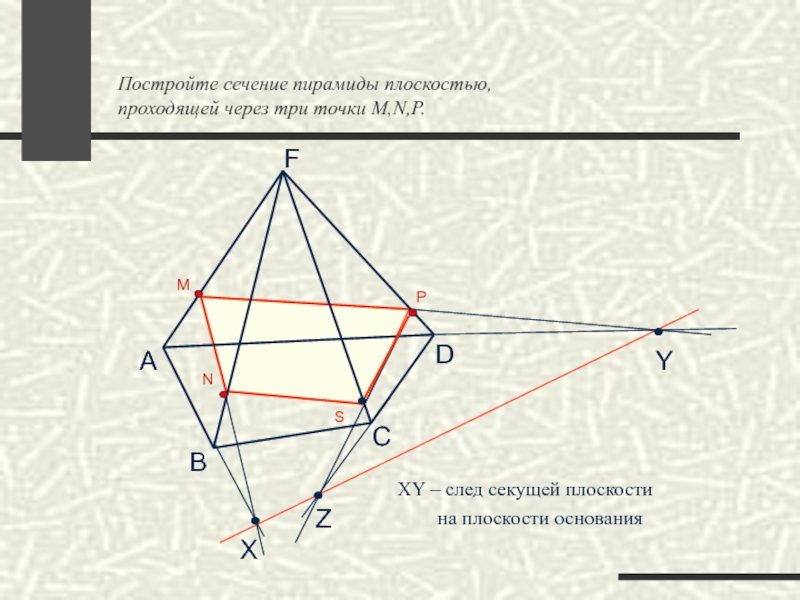
Постройте сечение пирамиды плоскостью,
проходящей через три точки M,N,P.
XY – след
на плоскости основания
D
C
B
А
Z
Y
X
M
N
P
S
F
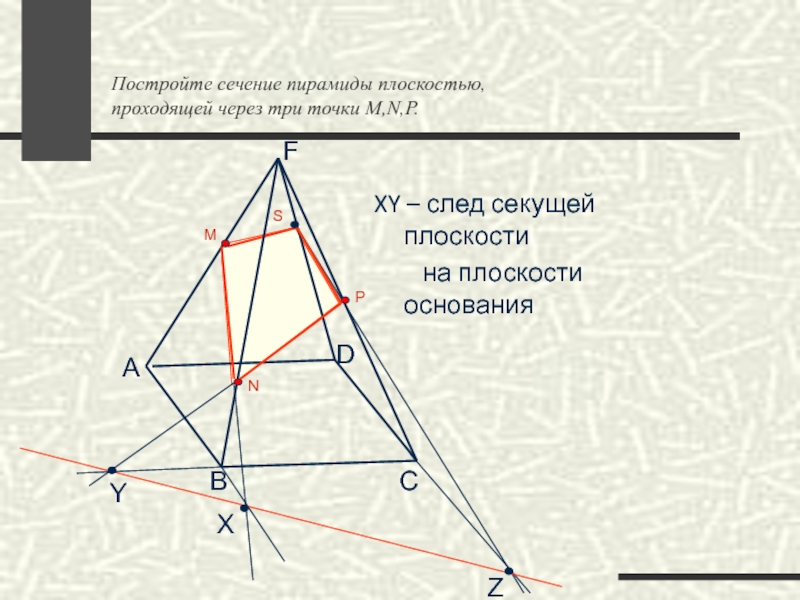
Слайд 92
XY – след секущей плоскости
на плоскости
D
C
B
Z
Y
X
M
N
P
S
Постройте сечение пирамиды плоскостью,
проходящей через три точки M,N,P.
А
F