- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
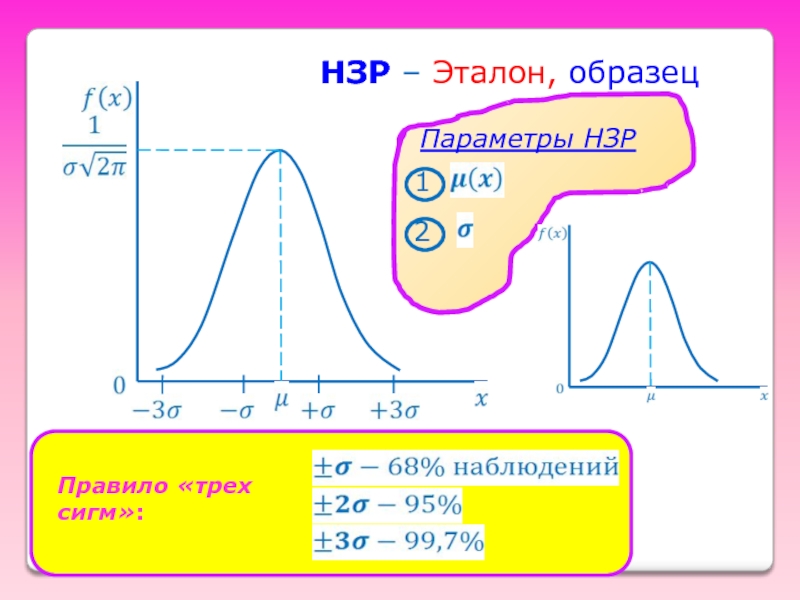
- Философия
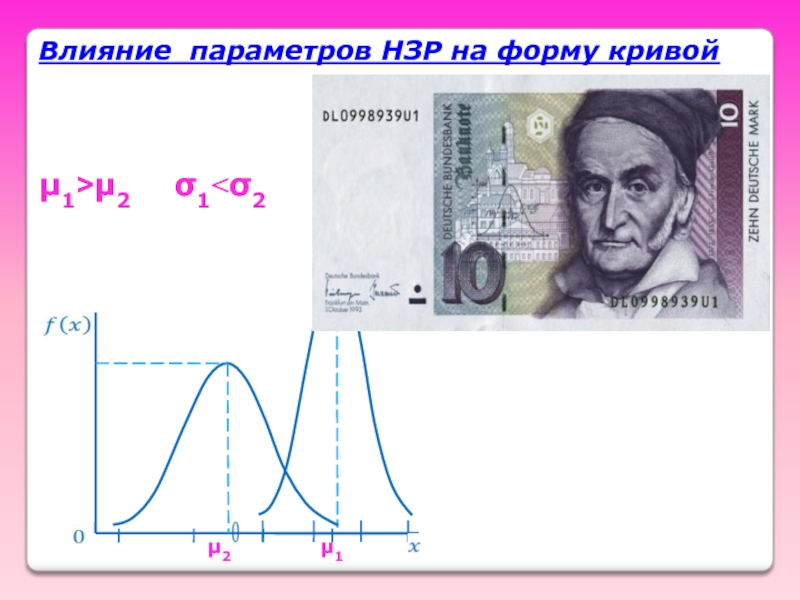
- Химия
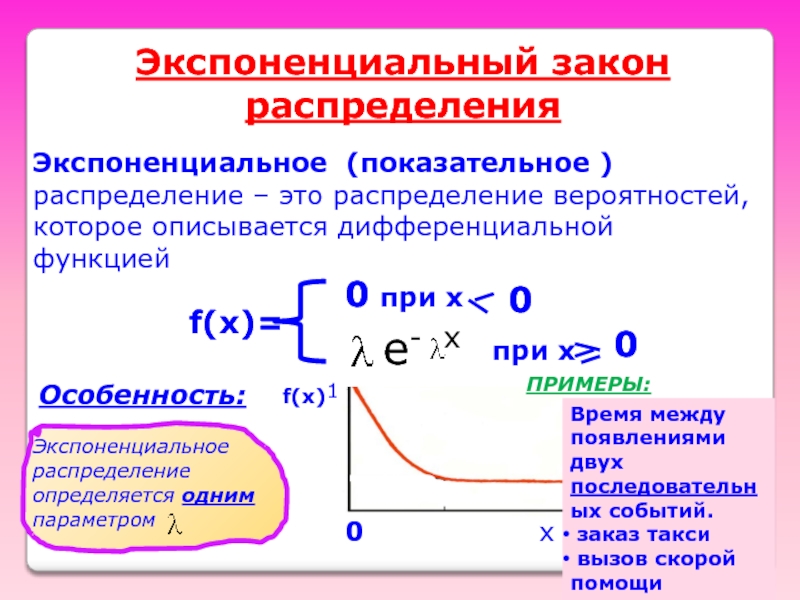
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории вероятностей. (Лекция 1) презентация
Содержание
- 2. Название читаемого курса: ФИЗИКА. МАТЕМАТИКА Специальность 060103 Педиатрия 6 модулей:
- 3. Лекция 1 Введение; Основы теории вероятностей Ростов-на-Дону 2012
- 4. Содержание лекции №1 Введение Основы
- 5. Прогресс в медицине тесно связан с применением
- 6. Леонардо да Винчи 1452-1519 гг. “Никакое человеческое
- 7. Если тебе хорошо дается математика и естественные
- 8. Основы теории вероятностей Теория вероятностей
- 9. Случайное событие Событие – это факт, который
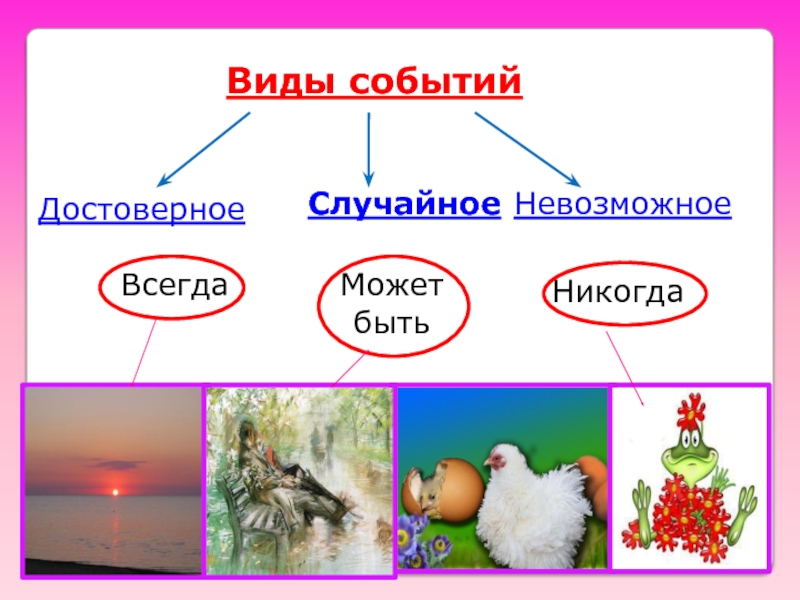
- 10. Виды событий Достоверное Случайное Невозможное
- 11. Какие события относятся к случайным? А. Появление
- 12. Вероятность случайного события
- 13. Английский математик Карл Пирсон бросал монету 24000
- 14. Свойства вероятности Рдост. (А)=1 Рневозм. (А)=0 0≤Р(А) ≤1
- 15. Набирая номер телефона абонент забыл одну цифру
- 16. Одна секретарша напечатала 5 различных писем
- 17. Понятие о несовместных и совместных событиях События
- 18. Понятие о независимых и зависимых событиях
- 19. Условия нормировки
- 20. Условная вероятность
- 21. Теорема сложения вероятностей вероятность совместности этих
- 22. В корзине 30 цветных рубашек: 10 красных,
- 23. Два стрелка. Вероятность попадания в цель
- 24. Теорема умножения вероятностей
- 25. Брошены 2 монеты. Какова
- 26. Известно, что в 3х случаях из 250
- 27. Человеческий организм – это вероятностная
- 28. “Диагноз является вопросом вероятности, и это слишком
- 29. Понятие о доказательной медицине Доказательная медицина
- 30. Случайные величины Дискретные Непрерывные Случайная величина -
- 31. Что в этом тесте дискретного,
- 32. Распределение дискретных и непрерывных случайных величин
- 33. Способы задания Табличный Аналитический Графический Требование: Для
- 34. Функция распределения Функция распределения = =
- 35. Плотность распределения вероятностей = дифференциальная функция распределения. Только для непрерывной случайной величины.
- 36. Характеристики случайных величин Математическое ожидание Для
- 37. Дисперсия – рассеяние вокруг математического ожидания
- 38. Среднее квадратичное отклонение Среднее квадратичное отклонение –
- 39. Пример.
- 40. Нормальный закон распределения (НЗР) = закон
- 41. НЗР – Эталон, образец
- 42. μ1˃μ2 σ1˂σ2 μ1 μ2 Влияние параметров НЗР на форму кривой
- 43. Экспоненциальный закон распределения Экспоненциальное (показательное )
Слайд 4Содержание лекции №1
Введение
Основы теории вероятностей
Случайные события
Случайные величины
Нормальный и экспоненциальный законы
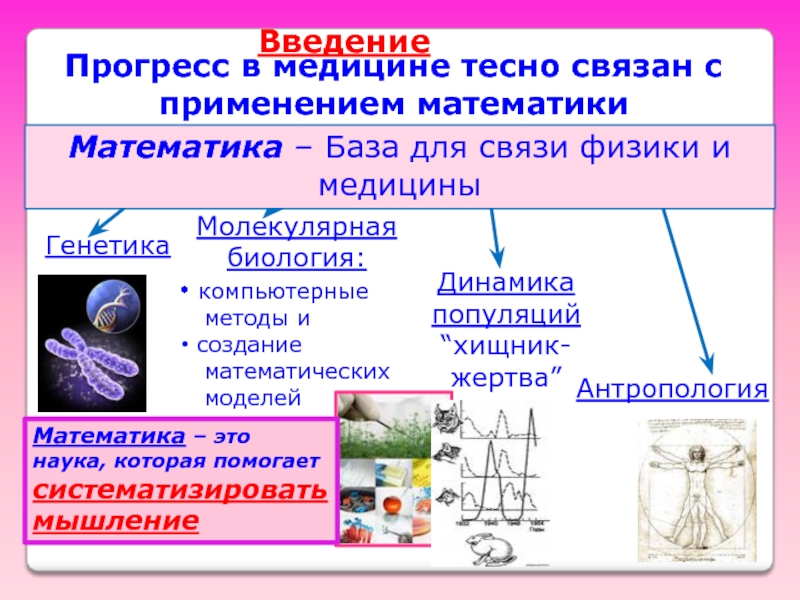
Слайд 5Прогресс в медицине тесно связан с применением математики
Генетика
Молекулярная
биология:
компьютерные
методы и
математических
моделей
Антропология
Динамика популяций “хищник-жертва”
Математика – это наука, которая помогает систематизировать мышление
Математика – База для связи физики и медицины
Введение
Слайд 6Леонардо да Винчи
1452-1519 гг.
“Никакое человеческое исследование не может почитаться истинной наукой,
“Книга о живописи”
Слайд 7Если тебе хорошо дается математика и естественные науки – становись врачом
Главный
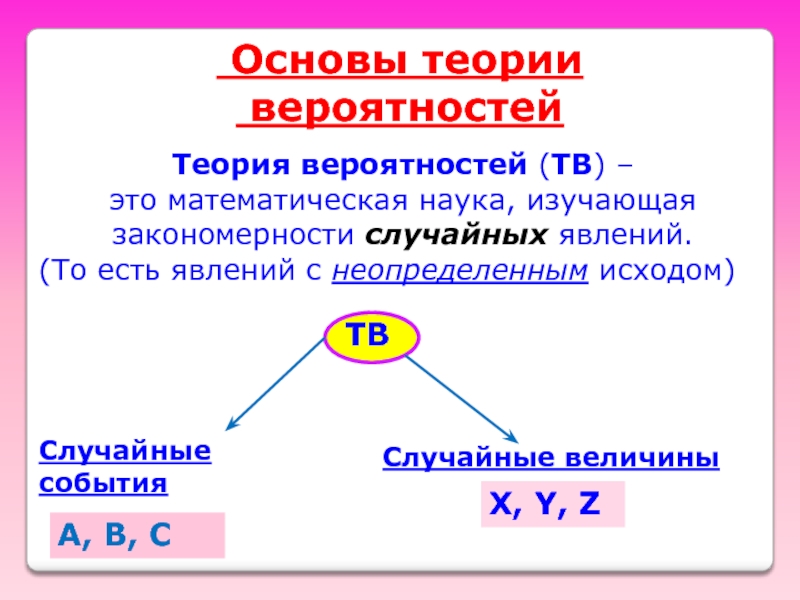
Слайд 8 Основы теории
вероятностей
Теория вероятностей (ТВ) –
это математическая наука, изучающая
закономерности
(То есть явлений с неопределенным исходом)
ТВ
Случайные события
A, B, C
Случайные величины
X, Y, Z
Слайд 9Случайное событие
Событие – это факт, который в результате
испытания может произойти
Это испытание
Это событие
Слайд 11Какие события относятся к
случайным?
А. Появление орла при
подбрасывании монеты
Б. Равномерное движение
материальной
В. Восход солнца
Г. Рождение мальчика
Ответ:
А, Г.
Слайд 12
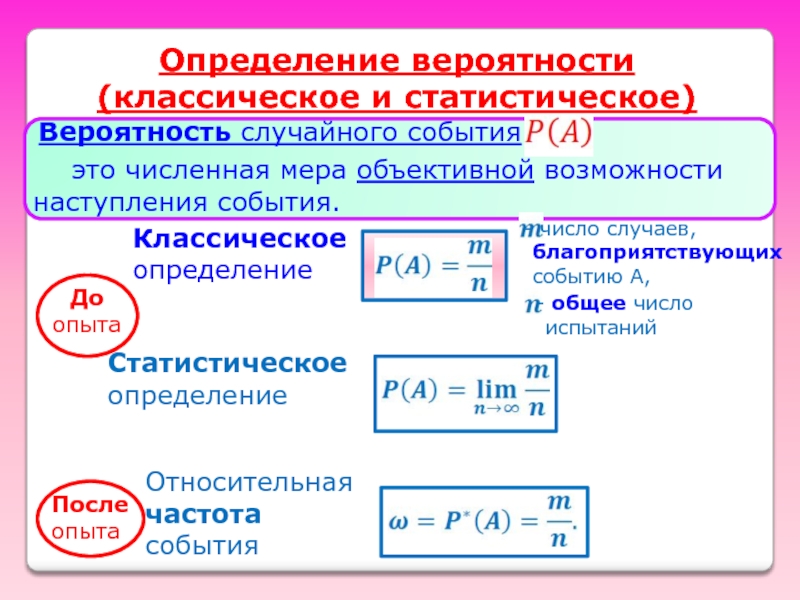
Вероятность случайного события
это численная мера объективной возможности
наступления
Классическое
определение
Статистическое
определение
Относительная частота
события
Определение вероятности (классическое и статистическое)
Слайд 13Английский математик Карл Пирсон бросал монету 24000 раз.
Герб выпал 12012
Какова частота выпадения герба?
Слайд 15Набирая номер телефона абонент
забыл одну цифру и набрал ее наугад.
Какова вероятность,
цифру правильно?
Ответ:
Слайд 16Одна секретарша напечатала 5
различных писем и надписала 5
конвертов с
что она вкладывает письма в конверты
случайным образом.
Какова вероятность, что ровно 4 письма
будут вложены в конверты с адресами
тех лиц, кому они предназначены?
Ответ:
Слайд 17Понятие о несовместных и совместных событиях
События А и В несовместны, если
ПРИМЕРЫ
События А и В совместны, если появление одного из них не исключает появления другого в одном и том же испытании .
ПРИМЕРЫ
Слайд 18Понятие о независимых и зависимых событиях
Два события называются независимыми, если
ПРИМЕРЫ
Два события называются зависимыми, если
вероятность одного из них зависит от появления другого.
Слайд 20Условная вероятность
Какова вероятность вытащить
подряд 2 белых шара?
А может ли быть
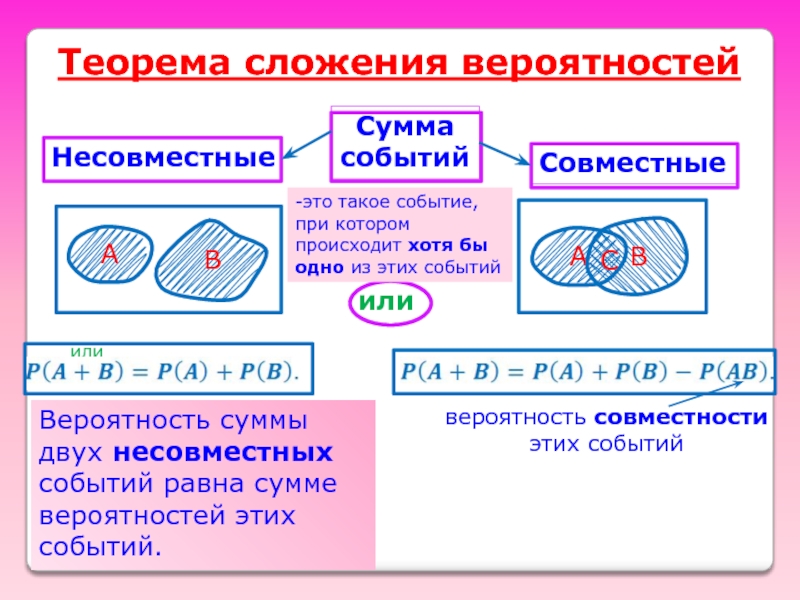
Слайд 21Теорема сложения вероятностей
вероятность совместности
этих событий
или
-это такое событие, при котором происходит
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Слайд 22В корзине 30 цветных рубашек:
10 красных, 5 синих, 15 белых.
Какова вероятность
цветную рубашку?
Ответ:
или
Слайд 23Два стрелка. Вероятность попадания в
цель 1го стрелка – 0,8, а
Какова вероятность, что при
одновременном выстреле цель будет
поражена. Цель считается пораженной
при попадании в нее хотя бы одной из
2х пуль.
Решение:
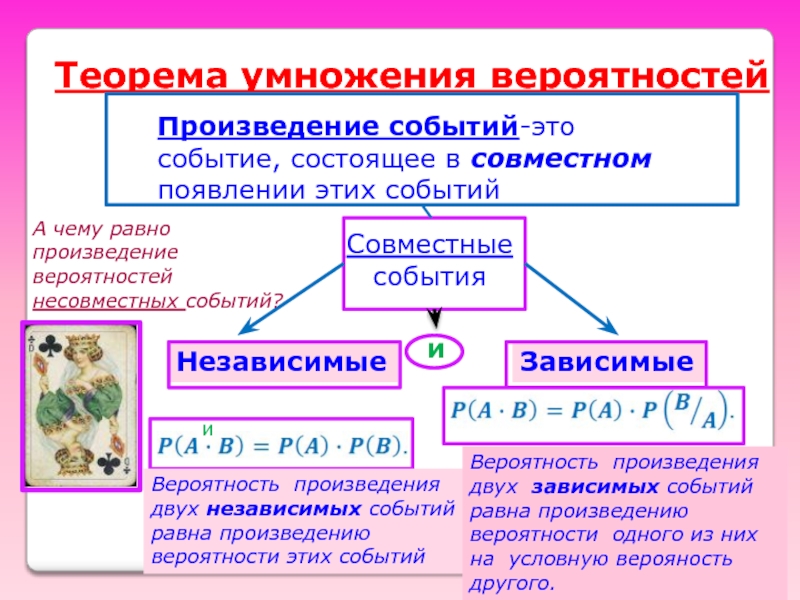
Слайд 24Теорема умножения вероятностей
и
А чему равно произведение вероятностей
несовместных событий?
Вероятность произведения двух
Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную верояность другого.
Слайд 25
Брошены 2 монеты.
Какова вероятность, что
“появился герб” и появилась
Ответ:
Брошены монеты и игральная кость.
Найти вероятность совмещения событий
“появился герб”, “появилось 6 очков”.
Ответ:
Слайд 26Известно, что в 3х случаях из 250 на свет
появляются близнецы.
одном из 3х – это истинные близнецы
(монозиготные).
Какова априорная вероятность того, что
у определенной беременной женщины
родятся близнецы мальчик и девочка, т.е.
дизиготные?
Решение:
Слайд 27
Человеческий организм – это вероятностная система.
Нет детерминированных показателей: что хорошо
Воздействие
Ему хорошо
Смерть
“Медицина – это наука
неопределенности и
искусство вероятности”.
Сэр Вильям Ослер
Слайд 28“Диагноз является вопросом вероятности, и это слишком хорошо знают те врачи,
Пиккеринг – выдающийся английский врач
Как можно использовать вероятность
для постановки диагноза?
Слайд 29
Понятие о доказательной медицине
Доказательная медицина (англ.Evidence-based medicine)– это медицина, основанная на
Это подход к медицинской практике, при котором решения о применении профилактических, диагностических и лечебных мероприятий принимаются исходя из имеющихся доказательств их эффективности и безопасности.
Такие доказательства подвергаются поиску, сравнению, обобщению и широкому распространению для использования в интересах больных.
Слайд 30Случайные величины
Дискретные
Непрерывные
Случайная величина - это величина, которая в результате испытания примет
Слайд 31
Что в этом тесте дискретного, а что
непрерывного?
Иванов – 170
Петров – 182 см
Сидоров – 167 см
Слайд 32Распределение дискретных и
непрерывных случайных величин
и их характеристики:
математическое ожидание,
дисперсия,
квадратическое отклонение
Распределение = закон распределения –
это совокупность значений случайной
величины и вероятностей их появления.
Слайд 33Способы задания
Табличный
Аналитический
Графический
Требование:
Для дискретных
случайных величин.
Функция распределения
Плотность распределения
вероятностей
Слайд 34
Функция распределения
Функция распределения = = интегральная функция распределения – это вероятность
Для дискретных
случайных величин
Для непрерывных
случайных величин
Для дискретной и непрерывной случайных величин.
Слайд 35
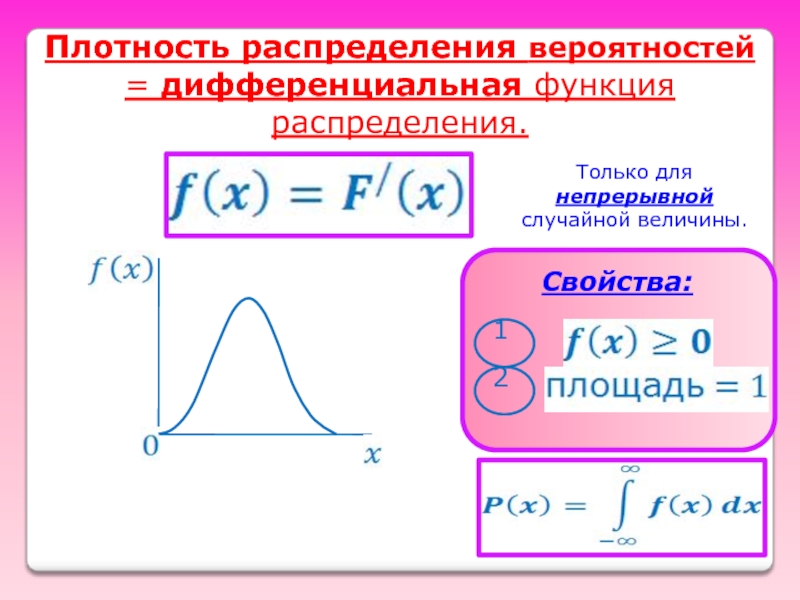
Плотность распределения вероятностей
= дифференциальная функция распределения.
Только для непрерывной
случайной величины.
Слайд 36 Характеристики случайных величин
Математическое ожидание
Для дискретных
случайных величин
Для непрерывных
случайных величин
Математическое ожидание
Слайд 37Дисперсия – рассеяние вокруг
математического ожидания
Для дискретных
случайных величин
Для непрерывных
случайных величин
Дисперсия –
отклонение
Слайд 38Среднее квадратичное отклонение
Среднее квадратичное отклонение – это корень квадратный из дисперсии.
Стандартное отклонение
Стандарт
Слайд 40Нормальный закон распределения
(НЗР) = закон Гаусса
НЗР – это распределение
вероятностей
случайной величины, которое
описывается
дифференциальной функцией
Карл Фридрих Гаусс
1777-1855 гг.
Звездный час Гаусса
в 8 лет!
или
1
2
.
.
99
100
1,2,3,.,18,..,99,100
Слайд 43
Экспоненциальный закон распределения
Экспоненциальное (показательное ) распределение – это распределение вероятностей, которое
f(x)=
0 при х
0
e- x
при х
0
Экспоненциальное распределение определяется одним параметром
Особенность:
х
f(x)
0
1
ПРИМЕРЫ:
Время между появлениями двух последовательных событий.
заказ такси
вызов скорой помощи