- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы прикладной теории упругости презентация
Содержание
- 1. Основы прикладной теории упругости
- 2. Напряженное состояние в точке
- 3. Напряженное состояние в точке Правила знаков Нормальные
- 4. Тензор напряжений Закон парности касательных напряжений На
- 5. Главные напряжения
- 6. Инварианты тензора напряжений Контроль правильности определения главных напряжений
- 7. Деформированное состояние в точке
- 8. Главные деформации
- 9. Объемная деформация – размеры параллелепипеда Размеры параллелепипеда после деформации
- 10. Уравнения связи деформаций и перемещений в декартовой
- 11. Уравнения Коши (геометрические уравнения)
- 12. Уравнения неразрывности деформаций Зависимости между составляющими деформаций в одной плоскости
- 13. Уравнения неразрывности деформаций Зависимости между составляющими деформаций в разных плоскостях
- 14. Уравнения неразрывности деформаций Все 6 компонентов деформаций
- 15. Обобщенный закон Гука
- 16. Обобщенный закон Гука
- 17. Обобщенный закон Гука
- 18. Основные гипотезы предельных состояний Предельное НС –
- 19. Коэффициент запаса прочности Под коэффициентом запаса понимается
- 20. 1. Гипотеза наибольшего нормального напряжения В качестве
- 21. 2. Гипотеза наибольших линейных деформаций Отрыв материала
- 22. 3. Гипотеза максимальных касательных напряжений Образование остаточных
- 23. 4. Гипотеза энергии формоизменения Внутренняя потенциальная энергия
- 24. 4. Гипотеза энергии формоизменения Гипотеза применима к
- 25. Теория прочности Мора Общепризнанной в настоящее время является теория прочности Мора
- 26. Дифференциальные уравнения равновесия в декартовой системе координат
- 27. Дифференциальные уравнения равновесия в декартовой системе координат
- 28. Дифференциальные уравнения равновесия в декартовой системе координат
- 29. Дифференциальные уравнения равновесия в декартовой системе координат
- 30. Дифференциальные уравнения равновесия в декартовой системе координат Статические уравнения равновесия
- 31. Формулировка линейной задачи теории упругости Статические (или динамические) уравнения равновесия
- 32. Формулировка линейной задачи теории упругости Геометрические уравнения
- 33. Формулировка линейной задачи теории упругости Физические уравнения
- 34. Запись основных соотношений теории упругости в цилиндрической
- 35. Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная задача) Физические соотношения:
- 36. Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная задача) Уравнения равновесия:
- 37. Математические модели решения задач теории упругости 1.
- 38. Методы решения линейной задачи теории упругости Метод
- 39. Метод перемещений
- 40. Уравнения Коши (геометрические уравнения)
- 41. Метод сил (модель ПНС) Уравнения равновесия: Геометрические уравнения
- 42. Метод сил (модель ПНС) Физические уравнения
- 43. Метод сил (модель ПНС) Используем уравнение неразрывности
- 44. Метод сил (модель ПНС)
- 45. Метод сил (модель ПНС) Уравнение Леви
- 46. Метод сил (модель ПНС) Система дифференциальных уравнений
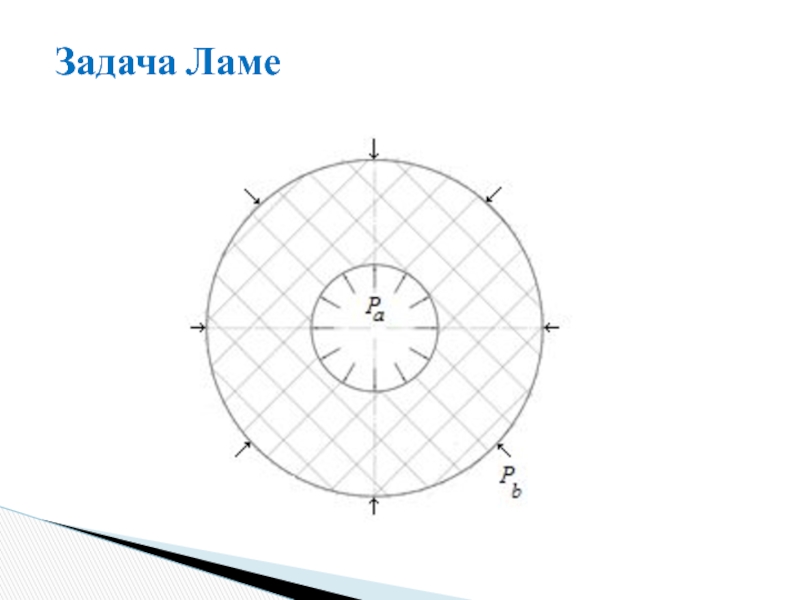
- 47. Задача Ламе
- 48. НДС прочноскрепленного заряда при действии внутреннего давления
- 49. Благодарю за внимание!
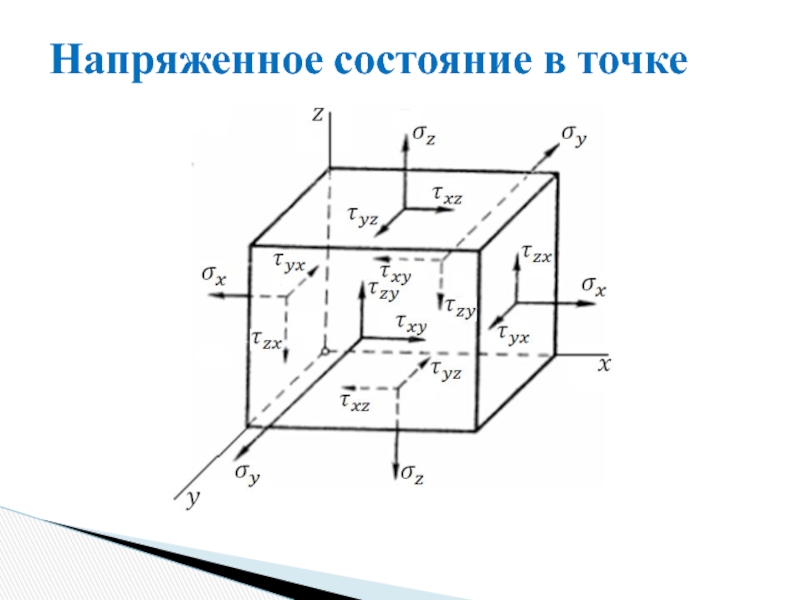
Слайд 3Напряженное состояние в точке
Правила знаков
Нормальные растягивающие напряжения считаются положительными, сжимающие –
За положительные составляющих касательных напряжений принимают положительные направления осей координат, если направление растягивающих нормальных напряжений по той же площадке совпадает с положительным направлением соответствующей оси координат.
Слайд 4Тензор напряжений
Закон парности касательных напряжений
На двух взаимно-перпендикулярных площадках составляющие касательных напряжений,
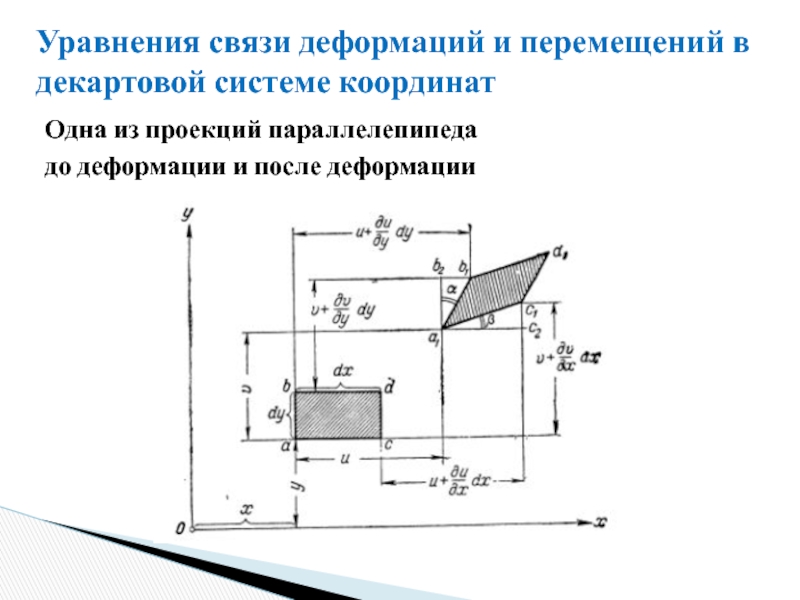
Слайд 10Уравнения связи деформаций и перемещений в декартовой системе координат
Одна из проекций
до деформации и после деформации
Слайд 12Уравнения неразрывности
деформаций
Зависимости между составляющими деформаций в одной плоскости
Слайд 13Уравнения неразрывности
деформаций
Зависимости между составляющими деформаций в разных плоскостях
Слайд 14Уравнения неразрывности
деформаций
Все 6 компонентов деформаций произвольно задавать нельзя. Между ними существуют
Физический смысл уравнений
Если, задаваясь деформациями, не учитывать уравнения неразрывности деформаций, и для каждого параллелепипеда, на которые мысленно разбито тело, назначить 6 независимых составляющих деформаций, то из отдельных таких деформированных параллелепипедов нельзя собрать непрерывного деформированного тела.
Тело, сплошное и непрерывное до деформации остается сплошным и непрерывным после деформации
Слайд 18Основные гипотезы
предельных состояний
Предельное НС – НС, при котором происходит качественное изменение
пластический материал – возникновение заметных остаточных деформаций;
хрупкий материал – начало разрушения материала.
Предельное НС может рассматриваться как характеристика свойств материала.
Трудность создания теории предельных состояний – недостаточность наших представлений о внутренних процессах, происходящих в материале.
Задача решается в основном путем анализа и обобщения экспериментальных данных.
2 направления в ТПС
на основе гипотез;
феноменологический подход (применяется при описании явлений, детальный механизм которых недостаточно ясен: физика – закон всемирного тяготения; геология – при описании закономерностей расположения залежей полезных ископаемых).
Слайд 19Коэффициент запаса прочности
Под коэффициентом запаса понимается число, показывающее, во сколько раз
Если в двух НС коэффициенты запаса равны, то такие НС называются равноопасными.
При растяжении
При сжатии
Слайд 201. Гипотеза наибольшего нормального напряжения
В качестве критерия прочности берется величина наибольшего
Два других главных не учитываются.
Слайд 212. Гипотеза наибольших линейных деформаций
Отрыв материала по плоскости можно рассматривать как
Была выдвинута гипотеза использовать в качестве ПС наибольшую линейную деформацию.
Эта гипотеза получила довольно широкое распространение, однако детальная проверка обнаружила в ней ряд существенных недостатков.
Слайд 223. Гипотеза максимальных касательных напряжений
Образование остаточных деформаций в металлах происходит сдвигом
Поэтому критерием перехода от упругого состояния в пластическое являются наибольшие касательные напряжения в точке.
Это означает, что пластические деформации начинают образовываться тогда, когда максимальные касательные напряжения достигают некоторого предельного значения
Пластичные материалы – удовлетворительные результаты.
Недостатки – для материалов, имеющих различные механические характеристики на растяжение и сжатие.
Слайд 234. Гипотеза энергии формоизменения
Внутренняя потенциальная энергия = энергия изменения объема +
В основе перехода из упругого состояния в пластическое учитывается только энергия формоизменения.
Слайд 244. Гипотеза энергии формоизменения
Гипотеза применима к оценке ПС пластичных материалов и
Гипотезы 3 и 4 являются основными гипотезами ПС и сохраняют свое значение до настоящего времени.
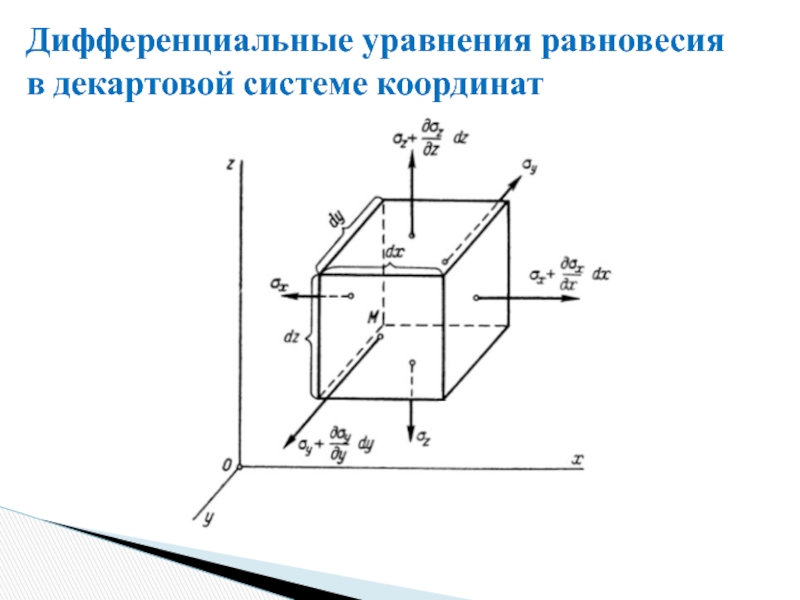
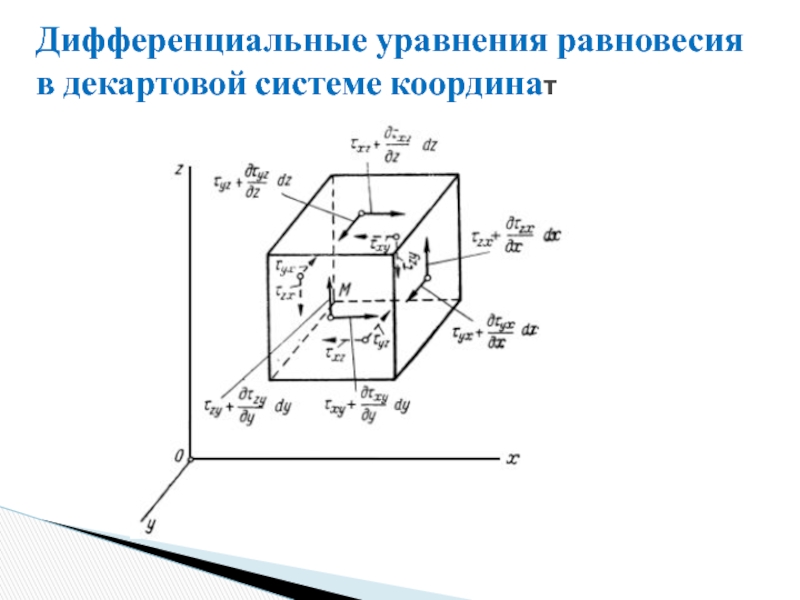
Слайд 28Дифференциальные уравнения равновесия
в декартовой системе координат
X – проекция на ось x
Слайд 30Дифференциальные уравнения равновесия
в декартовой системе координат
Статические уравнения равновесия
Слайд 31Формулировка линейной задачи
теории упругости
Статические (или динамические)
уравнения равновесия
Слайд 34Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная задача)
r,
u, w – перемещения.
Геометрические соотношения:
Слайд 35Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная задача)
Физические
Слайд 36Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная задача)
Уравнения
Слайд 37Математические модели решения задач теории упругости
1. Одномерные модели
Растяжение/сжатие, чистый сдвиг, кручение
2.
плоское напряженное состояние;
плоское деформированное состояние;
обобщенная плоская деформация.
3. Осесимметричная модель
4. Плоские осесимметричные модели
осесимметричное ПНС;
осесимметричное ПДС.
5. Трехмерная модель
Слайд 38Методы решения линейной задачи
теории упругости
Метод перемещений
из уравнений обобщенного закона Гука выразить
выразить напряжения через перемещения, используя геометрические соотношения;
подставить эти соотношения в уравнения равновесия.
Метод сил: основные неизвестные – напряжения.
Смешанный метод: за основные неизвестные приняты некоторые из перемещений и некоторые из напряжений.