СТАТИСТИКА. ТАБЛИЦЫ ДАННЫХ И МАНИПУЛЯЦИИ С НИМИ В РАЗЛИЧНЫХ СТАТИСТИЧЕСКИХ ПАКЕТАХ, ОБЗОР. ОПИСАТЕЛЬНАЯ СТАТИСТИКА В СТАТИСТИЧЕСКИХ ПРОГРАММАХ. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы практической биомедицинской статистики презентация
Содержание
- 1. Основы практической биомедицинской статистики
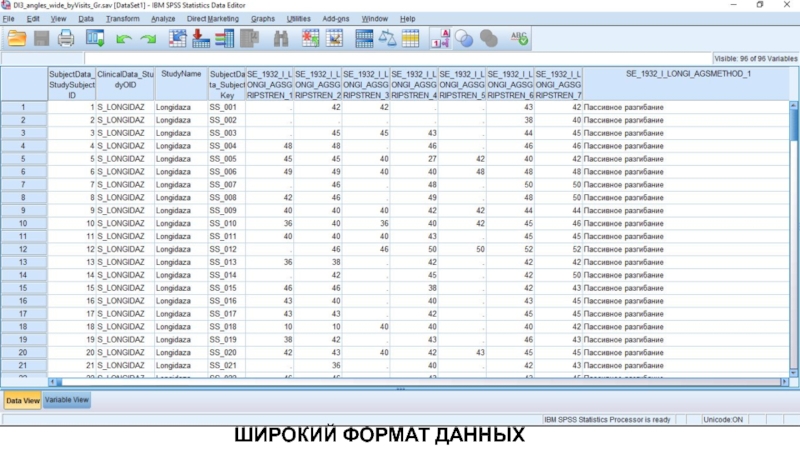
- 2. ШИРОКИЙ ФОРМАТ ДАННЫХ
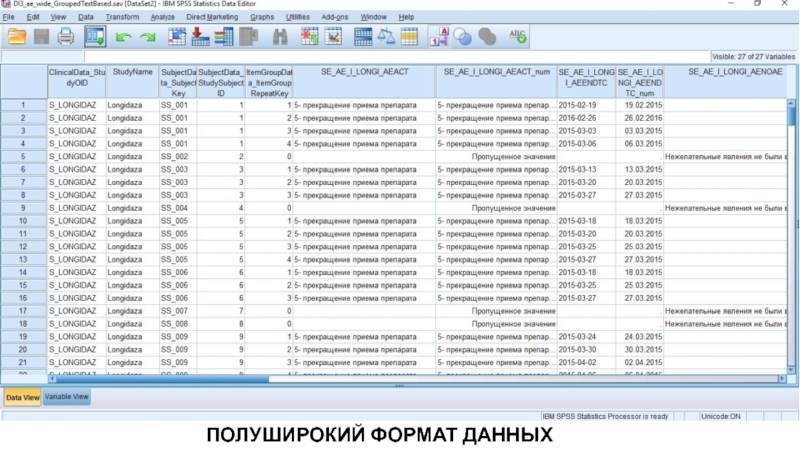
- 3. ПОЛУШИРОКИЙ ФОРМАТ ДАННЫХ
- 4. УЗКИЙ ФОРМАТ ДАННЫХ
- 5. Типы переменных Количественные (интервальные) – возможны все
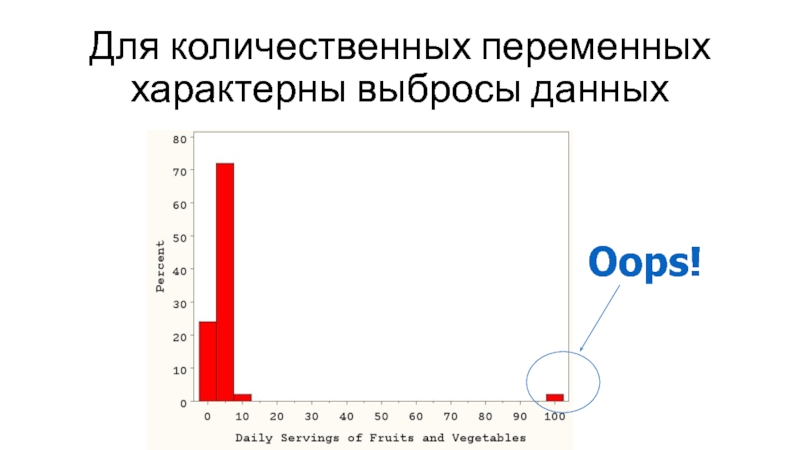
- 6. Для количественных переменных характерны выбросы данных
- 7. Тип шкалы: интервальная
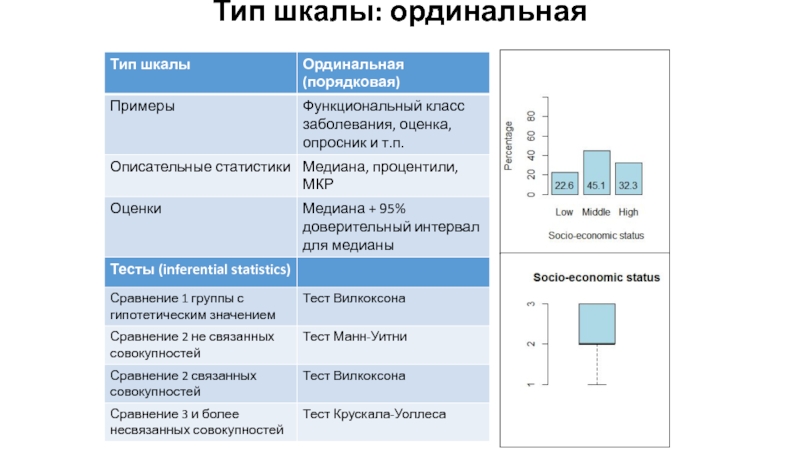
- 8. Тип шкалы: ординальная
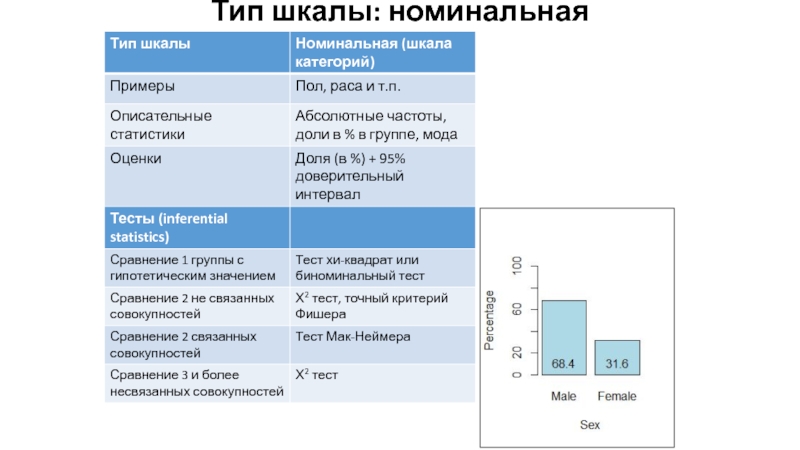
- 9. Тип шкалы: номинальная
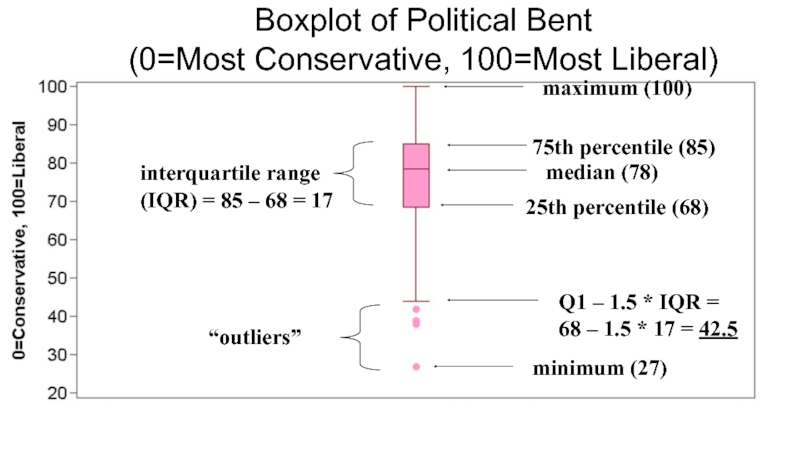
- 11. Boxplot of Political Bent (0=Most Conservative, 100=Most Liberal)
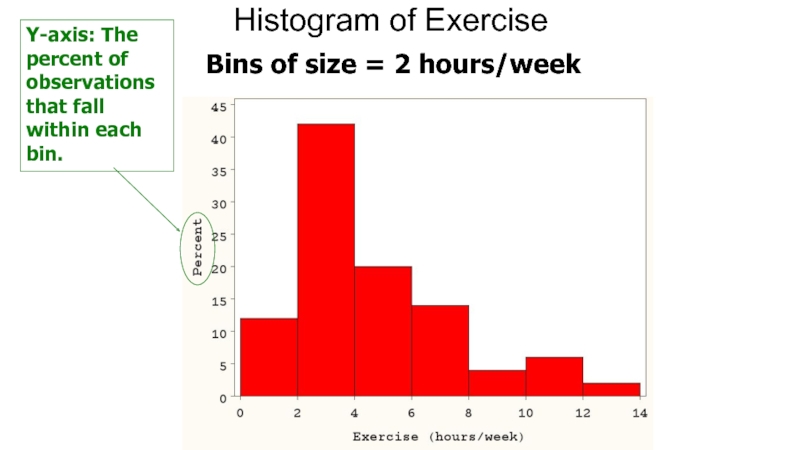
- 12. Bins of size = 2 hours/week Histogram of Exercise
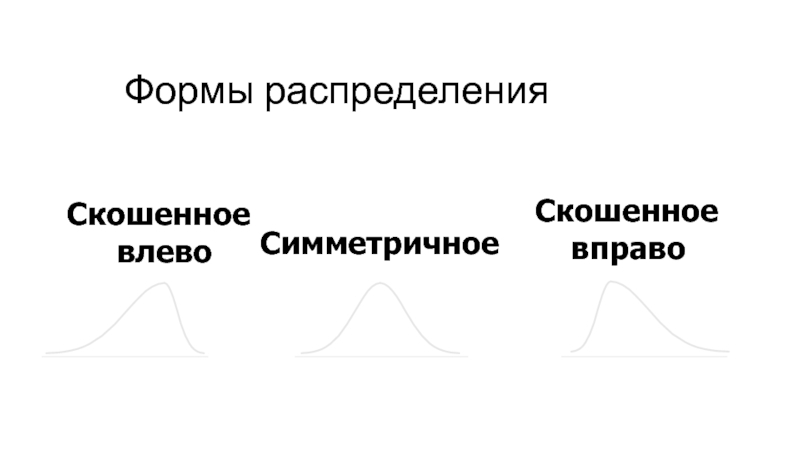
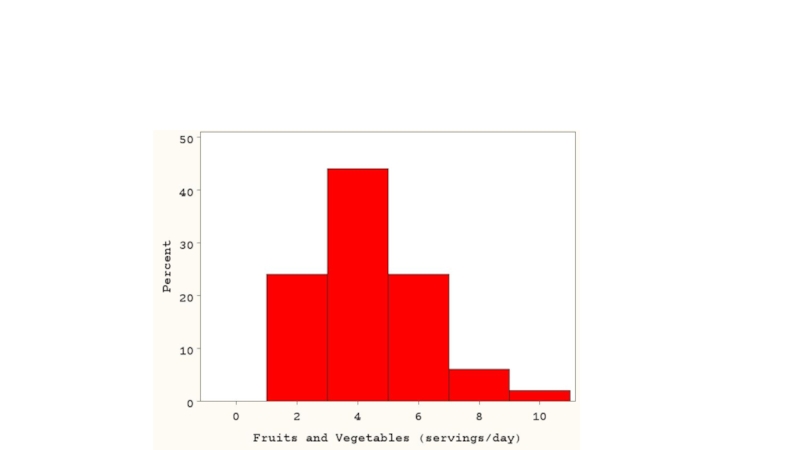
- 13. Формы распределения Скошенное вправо Скошенное влево Симметричное
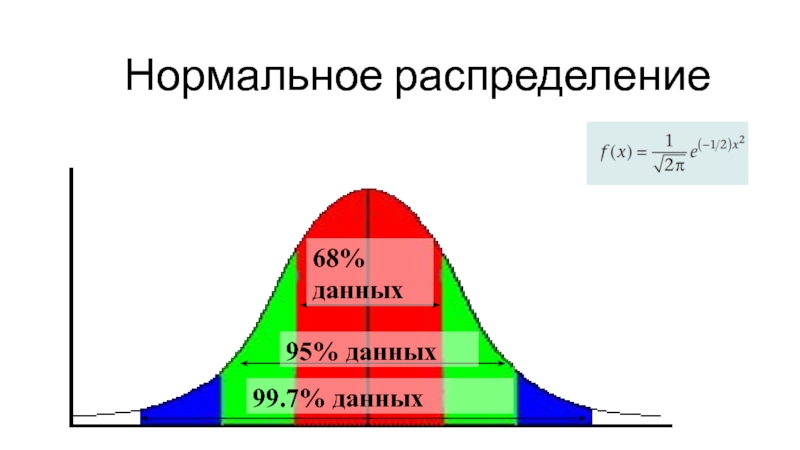
- 14. Нормальное распределение
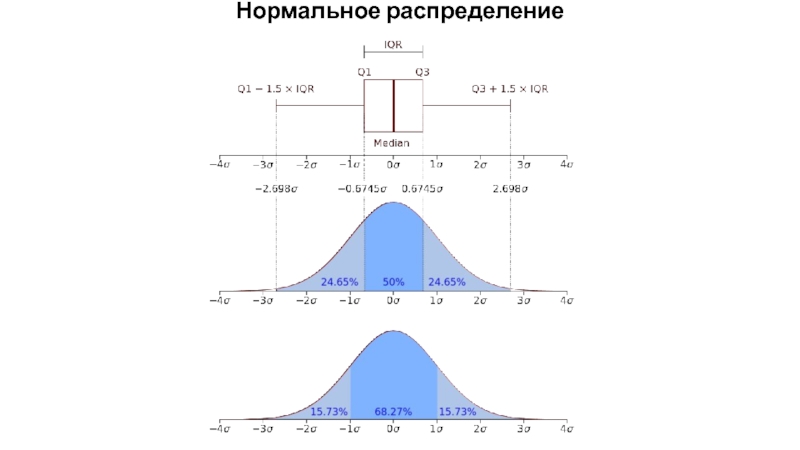
- 15. Нормальное распределение
- 20. Описательные статистики: меры центральной тенденции среднее арифметическое
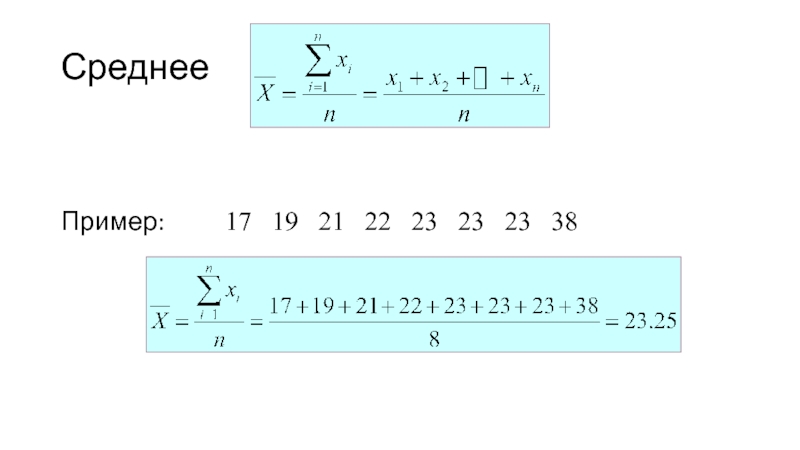
- 21. Среднее Пример: 17
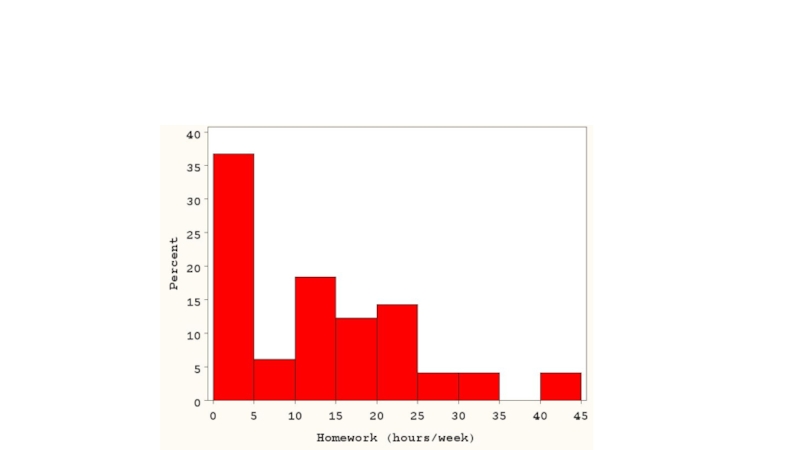
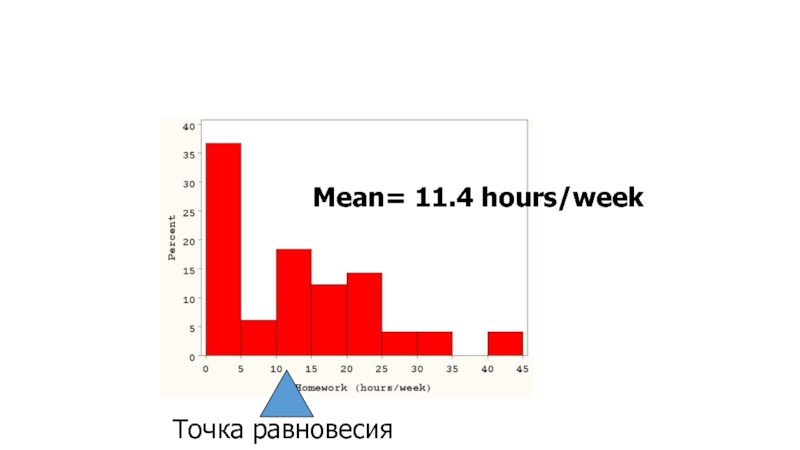
- 22. Mean= 11.4 hours/week
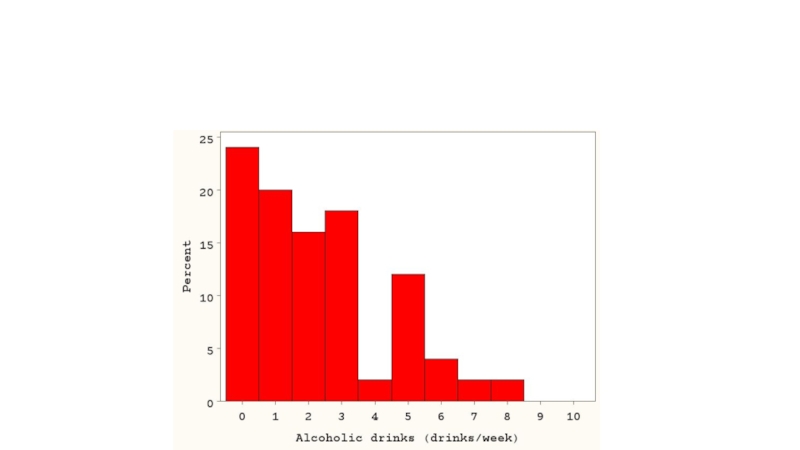
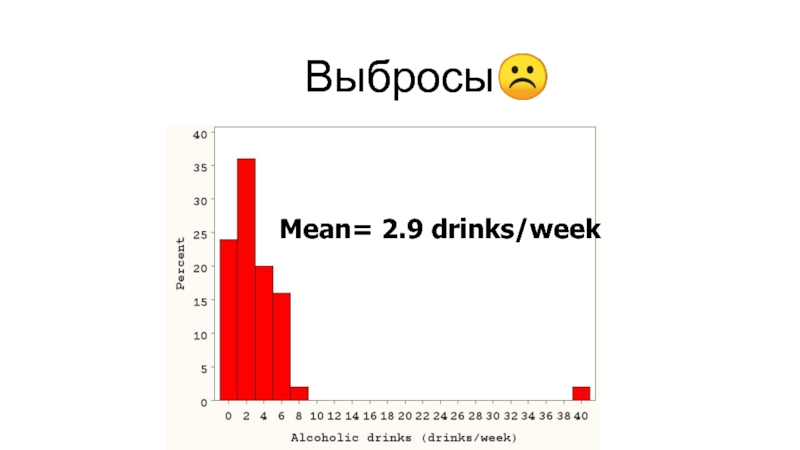
- 23. Выбросы☹ Mean= 2.9 drinks/week
- 24. МЕДИАНА Значение в середине распределения Расчет:
- 25. -30 -25 -20 -15 -10
- 26. -300 -280 -260 -240 -220
- 27. Меры разброса данных Меры рассеяния показывают, насколько
- 28. Дисперсия Стандартное отклонение
- 30. Стандартное отклонение и стандартная ошибка среднего Отклонение
- 31. Межквартильный размах Межквартильный размах = 3-й квартиль
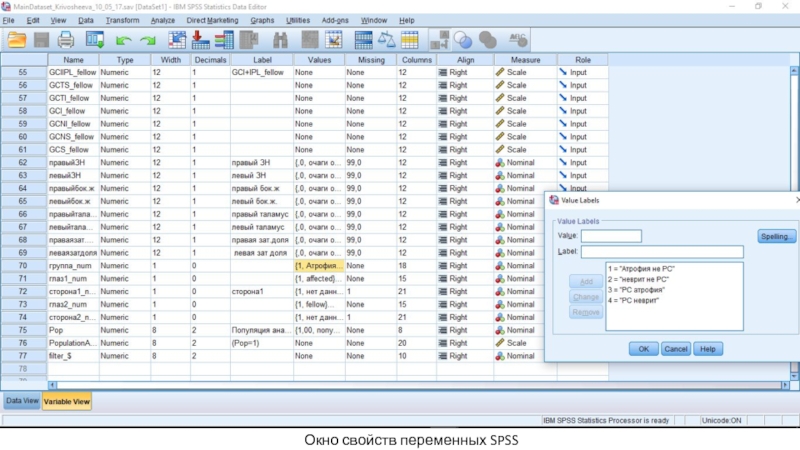
- 34. Окно свойств переменных SPSS
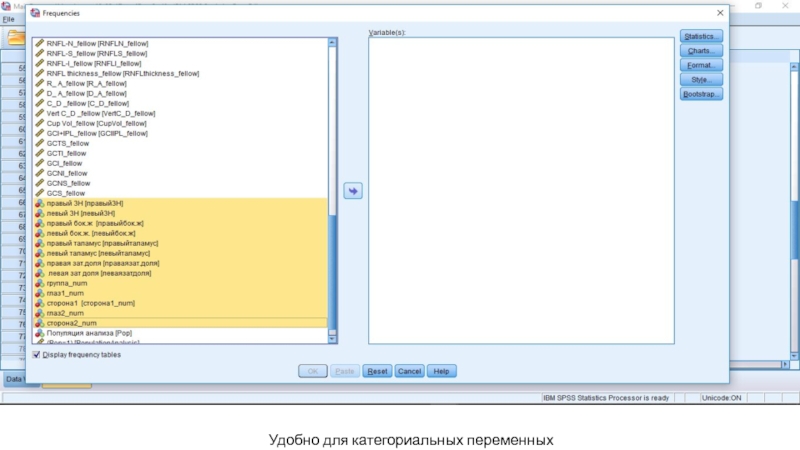
- 36. Удобно для категориальных переменных
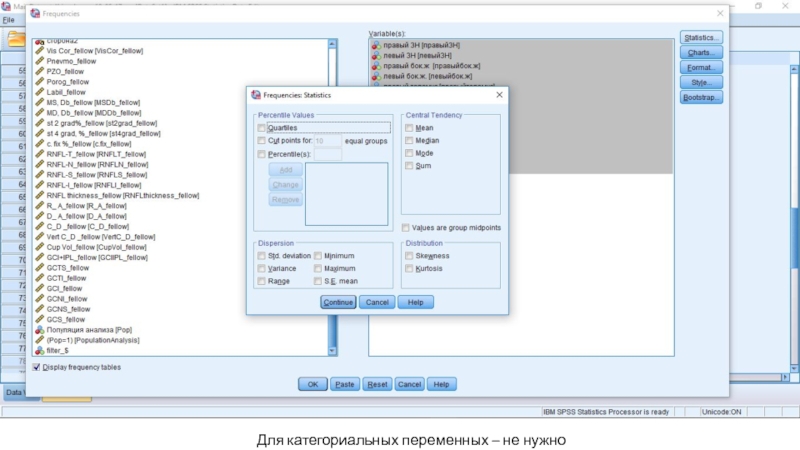
- 37. Для категориальных переменных – не нужно
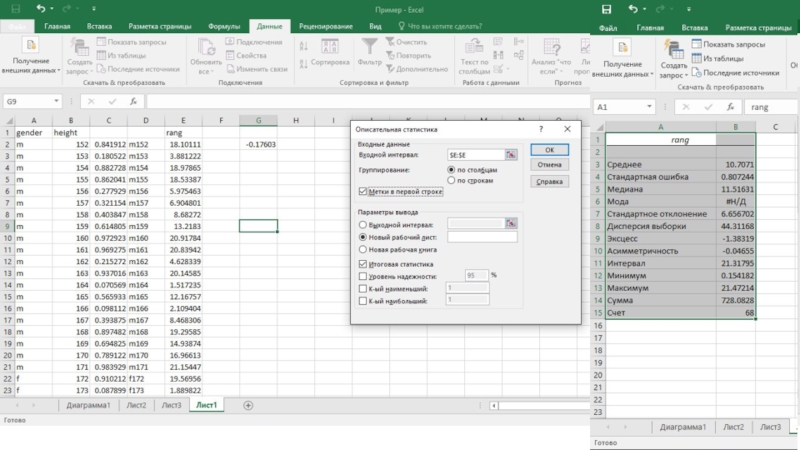
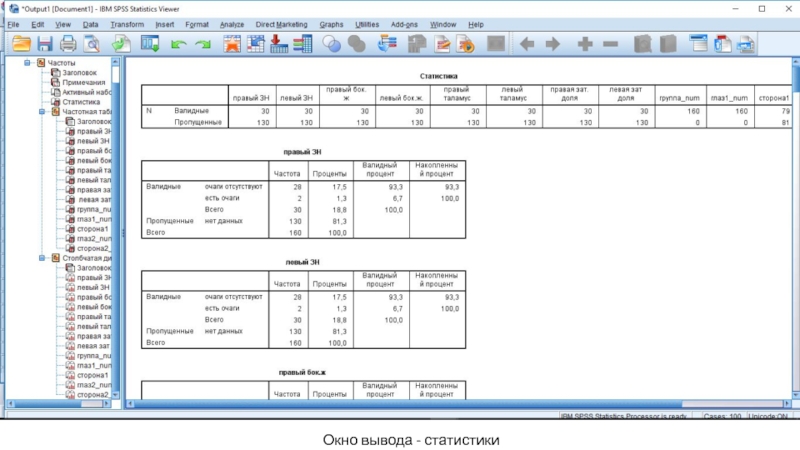
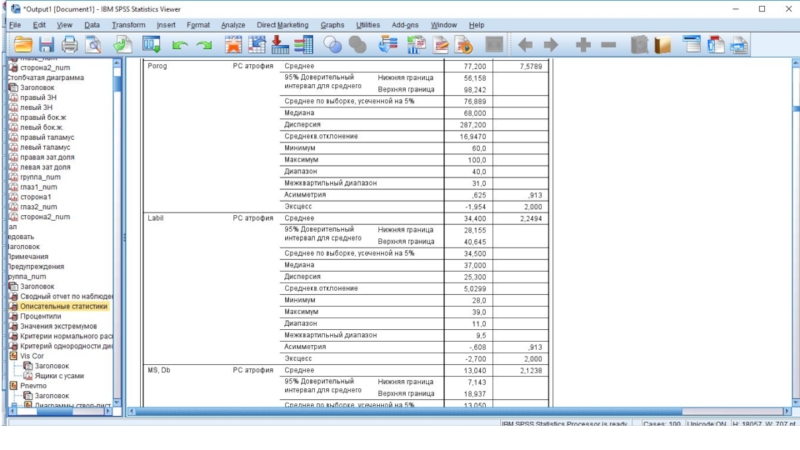
- 39. Окно вывода - статистики
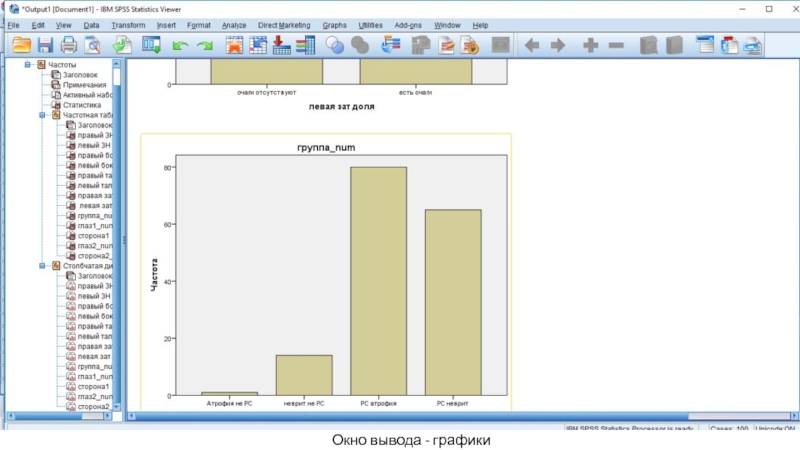
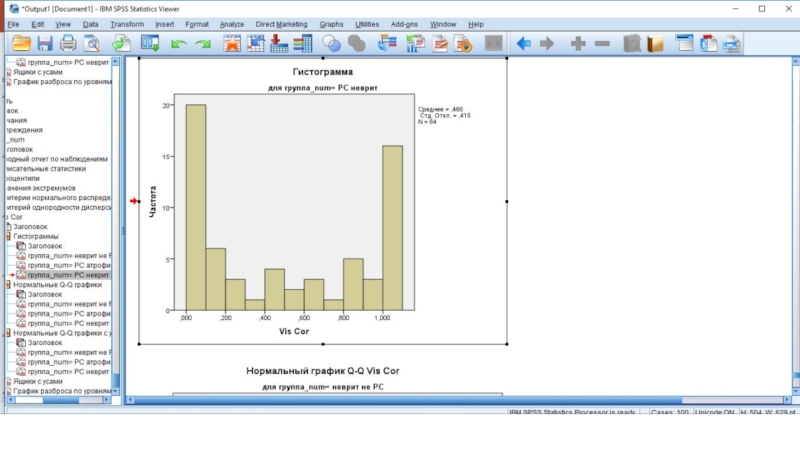
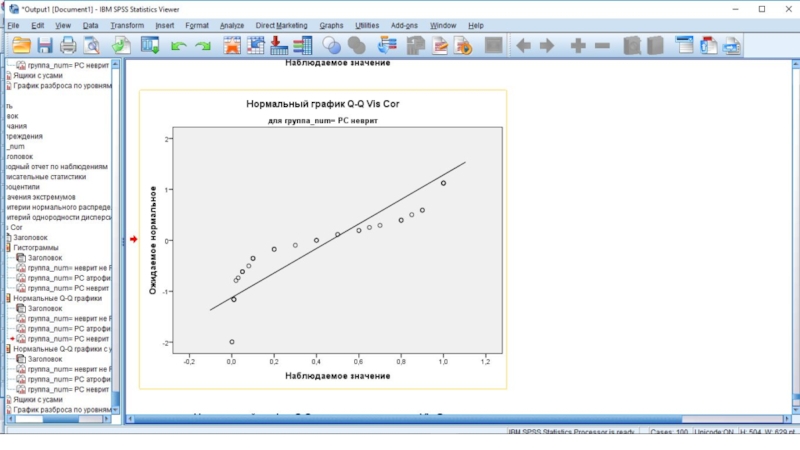
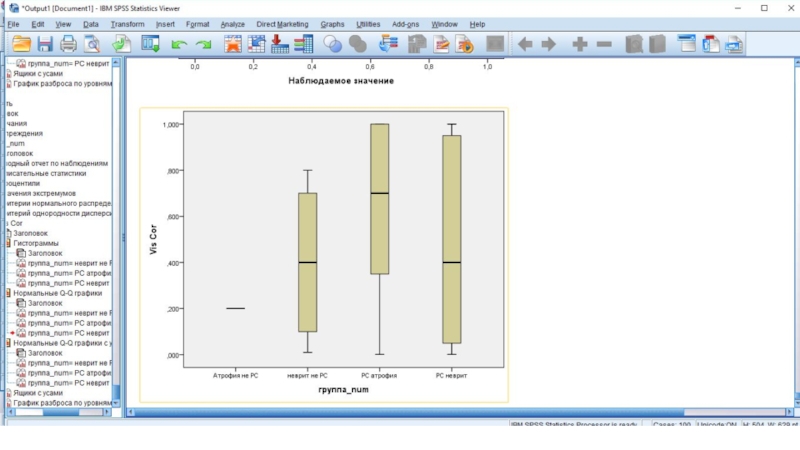
- 40. Окно вывода - графики
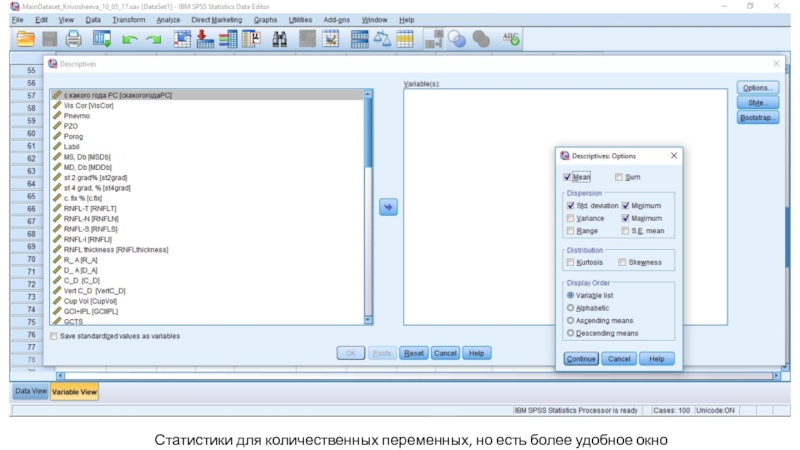
- 41. Статистики для количественных переменных, но есть более удобное окно
- 52. Стандартизованное Z-значение Ответ на вопрос «как далеко
- 53. Оценка среднего по выборочному среднему Приблизительно 95%
- 54. Общая формула для оценки интервала
- 55. Интерпретация доверительных интервалов На примере 95% ДИ
- 56. Доверительные интервалы Многими незаслуженно относятся к описательной
- 57. Исследователь Петрик рапортует: Robust misinterpretation of confidence
- 58. Какие из приведенных утверждений верны: Вероятность, что
- 59. Доверительные интервалы: ответы Вероятность, что истинное (популяционное)
ШИРОКИЙ ФОРМАТ ДАННЫХ
Слайд 1ОСНОВЫ ПРАКТИЧЕСКОЙ БИО-МЕДИЦИНСКОЙ СТАТИСТИКИ
СЕРИЯ 2
ПОНЯТИЕ ПЕРЕМЕННОЙ. ВИДЫ ПЕРЕМЕННЫХ. ТАБЛИЦЫ ДАННЫХ. ОПИСАТЕЛЬНАЯ
Слайд 5Типы переменных
Количественные (интервальные) – возможны все математические операции
Дискретные (что то в
штуках)
Непрерывные (возраст, АД, пульс)
Порядковые (ординальные) (стадия заболевания) - можно сказать что больше-меньше
Категориальные (качественные, номинальные) (цвета, группа крови)
Бинарные (выжил/умер, да/нет)
Непрерывные (возраст, АД, пульс)
Порядковые (ординальные) (стадия заболевания) - можно сказать что больше-меньше
Категориальные (качественные, номинальные) (цвета, группа крови)
Бинарные (выжил/умер, да/нет)
Уменьшение объема информации
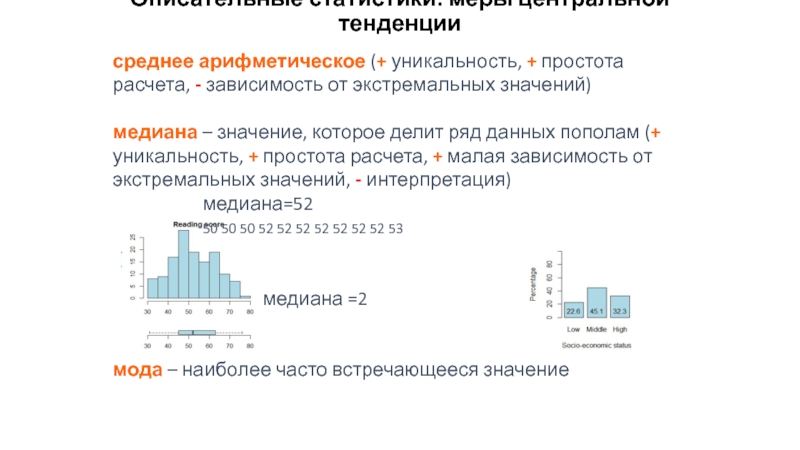
Слайд 20Описательные статистики: меры центральной тенденции
среднее арифметическое (+ уникальность, + простота расчета,
- зависимость от экстремальных значений)
медиана – значение, которое делит ряд данных пополам (+ уникальность, + простота расчета, + малая зависимость от экстремальных значений, - интерпретация)
медиана=52
50 50 50 52 52 52 52 52 52 52 53
медиана =2
мода – наиболее часто встречающееся значение
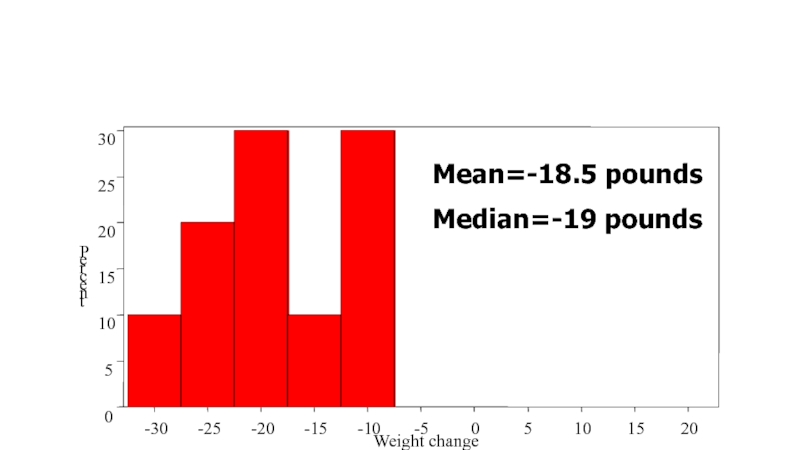
медиана – значение, которое делит ряд данных пополам (+ уникальность, + простота расчета, + малая зависимость от экстремальных значений, - интерпретация)
медиана=52
50 50 50 52 52 52 52 52 52 52 53
медиана =2
мода – наиболее часто встречающееся значение
Слайд 24МЕДИАНА
Значение в середине распределения
Расчет:
Среднее если нечетное число
Среднее между двумя средними
числами если четное.
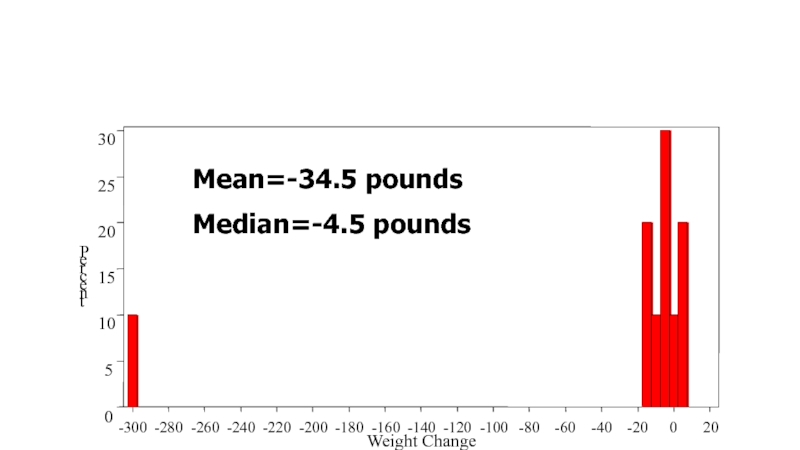
Слайд 26
-300
-280
-260
-240
-220
-200
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
0
5
10
15
20
25
30
P
e
r
c
e
n
t
Weight Change
Mean=-34.5 pounds
Median=-4.5 pounds
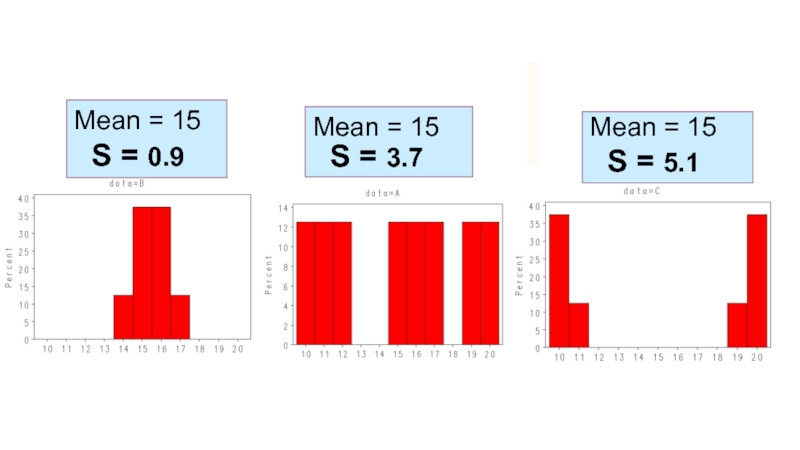
Слайд 27Меры разброса данных Меры рассеяния показывают, насколько хорошо данные значения представляют данную
совокупность
Размах
Стандартное отклонение
Перцентили
Межквартильный размах (IQR)
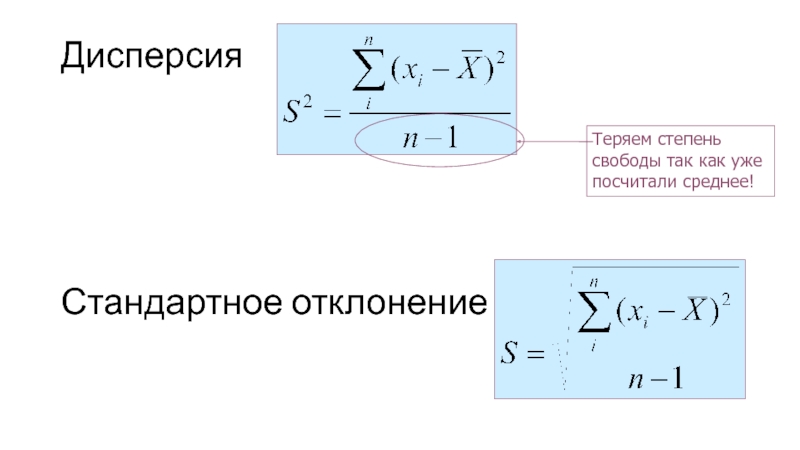
Слайд 30Стандартное отклонение и стандартная ошибка среднего
Отклонение – это разброс данных
Ошибка
– оценка истинного значения параметра, который рассчитывается ИСКУССТВЕННО
НЕ ПУТАТЬ!
Слайд 31Межквартильный размах
Межквартильный размах = 3-й квартиль – 1-й квартиль
Средние 50% данных
Выбросы
не влияют!
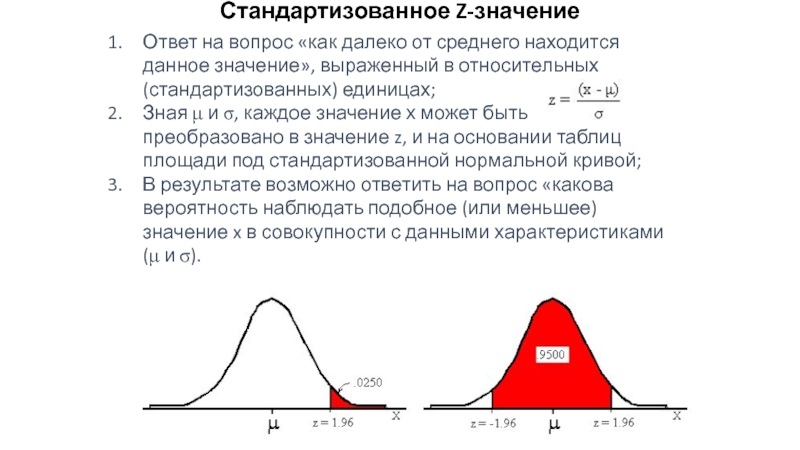
Слайд 52Стандартизованное Z-значение
Ответ на вопрос «как далеко от среднего находится данное значение»,
выраженный в относительных (стандартизованных) единицах;
Зная μ и σ, каждое значение х может быть преобразовано в значение z, и на основании таблиц площади под стандартизованной нормальной кривой;
В результате возможно ответить на вопрос «какова вероятность наблюдать подобное (или меньшее) значение x в совокупности с данными характеристиками (μ и σ).
Зная μ и σ, каждое значение х может быть преобразовано в значение z, и на основании таблиц площади под стандартизованной нормальной кривой;
В результате возможно ответить на вопрос «какова вероятность наблюдать подобное (или меньшее) значение x в совокупности с данными характеристиками (μ и σ).
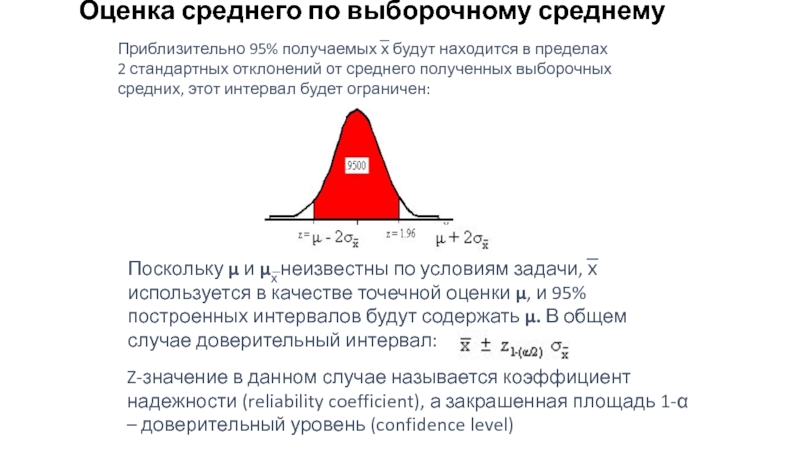
Слайд 53Оценка среднего по выборочному среднему
Приблизительно 95% получаемых x̅ будут находится в
пределах
2 стандартных отклонений от среднего полученных выборочных средних, этот интервал будет ограничен:
Поскольку µ и µx̅ неизвестны по условиям задачи, x̅ используется в качестве точечной оценки µ, и 95% построенных интервалов будут содержать µ. В общем случае доверительный интервал:
Z-значение в данном случае называется коэффициент надежности (reliability coefficient), а закрашенная площадь 1-α – доверительный уровень (confidence level)
Слайд 55Интерпретация доверительных интервалов
На примере 95% ДИ для среднего:
Интервальная оценка μ вычисляется
по формуле:
Если α=0.05, мы можем сказать, что при повторном отборе выборки, 95% полученных интервалов будут включать μ. Это заключение основано на вероятности получения различных значений x̅.
Если α=0.05, мы можем сказать, что при повторном отборе выборки, 95% полученных интервалов будут включать μ. Это заключение основано на вероятности получения различных значений x̅.
Слайд 56Доверительные интервалы
Многими незаслуженно относятся к описательной статистике
ДИ – численный интервал, построенный
вокруг оценки параметра по определенной методике
В силу этого он характеризует, в первую очередь, методику
Во вторую очередь он характеризует данные
В последнюю очередь – параметры популяционного показателя
В силу этого он характеризует, в первую очередь, методику
Во вторую очередь он характеризует данные
В последнюю очередь – параметры популяционного показателя
Слайд 57Исследователь Петрик рапортует:
Robust misinterpretation of confidence intervals. Hoekstra R1, Morey RD,
Rouder JN, Wagenmakers EJ. Psychon Bull Rev. 2014 Jan 14.
Слайд 58Какие из приведенных утверждений верны:
Вероятность, что истинное (популяционное) среднее больше 0,
как минимум, 95%
Вероятность, что истинное среднее равно 0 меньше 5%
Нулевая гипотеза, что истинное среднее равно 0, вероятно, будет отвергнута
С 95% вероятностью истинное среднее находится между 0,1 и 0,4
Мы можем быть на 95% уверены, что истинное среднее находится между 0,1 и 0,4
Если бы мы повторяли эксперимент снова и снова, 95% времени истинное среднее находилось бы в интервале 0,1 – 0,4
Вероятность, что истинное среднее равно 0 меньше 5%
Нулевая гипотеза, что истинное среднее равно 0, вероятно, будет отвергнута
С 95% вероятностью истинное среднее находится между 0,1 и 0,4
Мы можем быть на 95% уверены, что истинное среднее находится между 0,1 и 0,4
Если бы мы повторяли эксперимент снова и снова, 95% времени истинное среднее находилось бы в интервале 0,1 – 0,4
Слайд 59Доверительные интервалы: ответы
Вероятность, что истинное (популяционное) среднее больше 0, как минимум,
95%
Вероятность, что истинное среднее равно 0 меньше 5%
Присвоение вероятности параметру
Нулевая гипотеза, что истинное среднее равно 0, вероятно, неверна
Присвоение вероятности гипотезе
С 95% вероятностью истинное среднее находится между 0,1 и 0,4
Присвоение вероятности параметру
Мы можем быть на 95% уверены, что истинное среднее находится между 0,1 и 0,4
Если бы мы повторяли эксперимент снова и снова, 95% времени истинное среднее находилось бы в интервале 0,1 – 0,4
Утверждение относительно границ истинного среднего
Если бы мы повторяли эксперимент снова и снова, 95% времени (в 95% случаев) доверительные интервалы содержали бы истинное среднее
Вероятность, что истинное среднее равно 0 меньше 5%
Присвоение вероятности параметру
Нулевая гипотеза, что истинное среднее равно 0, вероятно, неверна
Присвоение вероятности гипотезе
С 95% вероятностью истинное среднее находится между 0,1 и 0,4
Присвоение вероятности параметру
Мы можем быть на 95% уверены, что истинное среднее находится между 0,1 и 0,4
Если бы мы повторяли эксперимент снова и снова, 95% времени истинное среднее находилось бы в интервале 0,1 – 0,4
Утверждение относительно границ истинного среднего
Если бы мы повторяли эксперимент снова и снова, 95% времени (в 95% случаев) доверительные интервалы содержали бы истинное среднее
