Факультет Заочный
Направление 38.03.02 «Менеджмент»
Кафедра Землеустройства
Дисциплина «Математические методы в экономике»
Лекция 1. Основы математического моделирования
Лектор: доцент кафедры землеустройства,
к.э.н. Сорокина Ольга Анатольевна
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы математического моделирования презентация
Содержание
- 1. Основы математического моделирования
- 2. Основная и дополнительная литература дисциплины Волков С.Н.
- 3. План лекции Понятие модели и экономико-математического моделирования.
- 4. 1. Понятие модели и экономико-математического моделирования
- 5. 1. Понятие модели и экономико-математического моделирования Математические
- 6. 2.Виды и классы моделей, применяемые в экономике.
- 7. 2.Виды и классы моделей, применяемые в экономике.
- 8. 2.Виды и классы моделей, применяемые в экономике.
- 9. 2.Виды и классы моделей, применяемые в экономике.
- 10. 2.Виды и классы моделей, применяемые в экономике.
- 11. 2.Виды и классы моделей, применяемые в экономике.
- 12. 2.Виды и классы моделей, применяемые в экономике.
- 13. 3.Требования, предъявляемые к использованию математических методов и
- 14. 4.Стадии экономико-математического моделирования Процесс решения задач
- 15. Спасибо за внимание!
Слайд 1МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального
образования
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПО ЗЕМЛЕУСТРОЙСТВУ»
Слайд 2Основная и дополнительная литература дисциплины
Волков С.Н. Экономико-математические методы в землеустройстве. –
М.: Колос, 2007. – 696 с.
Волков С.Н. Землеустройство. Экономико-математические методы и модели. Т.4. - М.: Колос, 2001.-696 с. (Учебники и учебные пособия для студентов высш. учеб. заведений).
Электронная версия учебного пособия Волков С.Н. Землеустройство. Экономико-математические методы и модели. –М.: ЦДМО ГУЗ, 2014.
Волков С.Н. Землеустройство. Экономико-математические методы и модели. Т.4. - М.: Колос, 2001.-696 с. (Учебники и учебные пособия для студентов высш. учеб. заведений).
Электронная версия учебного пособия Волков С.Н. Землеустройство. Экономико-математические методы и модели. –М.: ЦДМО ГУЗ, 2014.
Слайд 3План лекции
Понятие модели и экономико-математического моделирования.
Виды и классы моделей, применяемые в
землеустройстве.
Стадии экономико-математического моделирования.
Стадии экономико-математического моделирования.
Слайд 41. Понятие модели и экономико-математического моделирования
Термин модель происходит от латинского
слова «modulus» - образец, норма, мера. В науке этот термин связывается с таким методом научного познания как аналогия.
Следовательно, модель - это аналог чего-либо.
Математические модели, представляют собой абстрактные описания объектов, явлений или процессов с помощью знаков, символов.
Математические модели имеют вид некоторой совокупности математических уравнений или неравенств, таблиц, матриц, формул и других результатов математического описания тех или иных объектов, явлений или процессов.
Математические модели применяются, как правило, в тех случаях, когда геометрическое или физическое моделирование объекта затруднено или невозможно вообще.
Следовательно, модель - это аналог чего-либо.
Математические модели, представляют собой абстрактные описания объектов, явлений или процессов с помощью знаков, символов.
Математические модели имеют вид некоторой совокупности математических уравнений или неравенств, таблиц, матриц, формул и других результатов математического описания тех или иных объектов, явлений или процессов.
Математические модели применяются, как правило, в тех случаях, когда геометрическое или физическое моделирование объекта затруднено или невозможно вообще.
Слайд 51. Понятие модели и экономико-математического моделирования
Математические модели, применяемые в экономических исследованиях,
получили название экономико-математических.
Часть этих моделей стала эффективно применяться и в других научных сферах, например, в экономике, геодезии, землеустройстве и кадастрах.
Экономико-математическое моделирование – это способ построения экономико-математической модели изучаемого экономического явления
Часть этих моделей стала эффективно применяться и в других научных сферах, например, в экономике, геодезии, землеустройстве и кадастрах.
Экономико-математическое моделирование – это способ построения экономико-математической модели изучаемого экономического явления
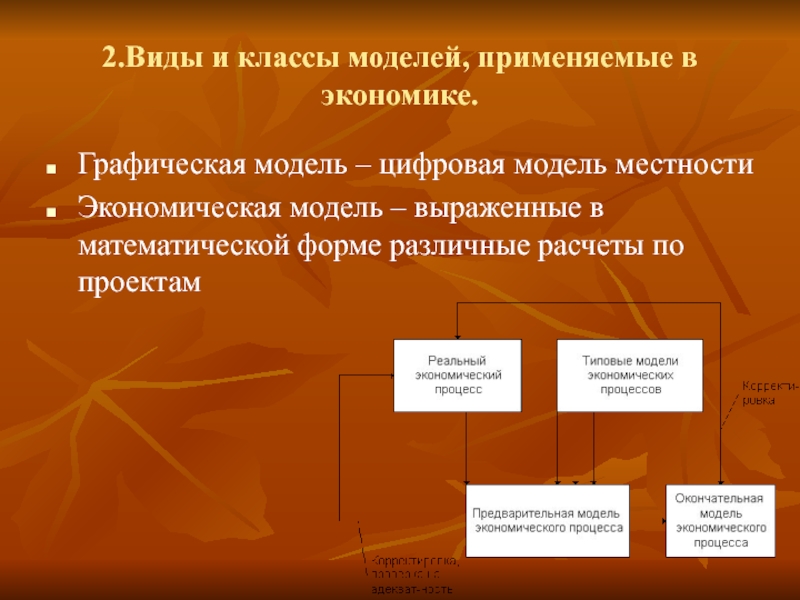
Слайд 72.Виды и классы моделей, применяемые в экономике.
Графическая модель – цифровая модель
местности
Экономическая модель – выраженные в математической форме различные расчеты по проектам
Экономическая модель – выраженные в математической форме различные расчеты по проектам
Слайд 82.Виды и классы моделей, применяемые в экономике.
К детерминистическим относятся модели, в
которых результат полностью и однозначно определяется набором независимых переменных. Эти модели строились на основе правил линейной алгебры и представляли собой системы уравнений, совместно решаемых для получения результатов.
К стохастическим относятся модели, описывающие случайные процессы, подчиняющиеся законам теории вероятностей. Это модели, основанные на выравнивании статистических рядов, а также модели, с помощью которых анализируются закономерности, не выражающиеся строго функциональными связями.
К стохастическим относятся модели, описывающие случайные процессы, подчиняющиеся законам теории вероятностей. Это модели, основанные на выравнивании статистических рядов, а также модели, с помощью которых анализируются закономерности, не выражающиеся строго функциональными связями.
Слайд 92.Виды и классы моделей, применяемые в экономике.
Аналитическая модель основана на применении
классического математического аппарата (алгебра, геометрия, мат.анализ). Рассчитывают средние расстояния, коэффициент компактности землепользования и др.
Экономико-статистическая модель основана на использовании статистической информации, сборе статистических данных. (Оценить зависимость урожайности сельскохозяйственной культуры от балла экономической оценки земель по этой культуре. При этом подбирается статистика по урожайности и баллам оценки с-х культуры за последние 12-15 лет.
Экономико-статистическая модель основана на использовании статистической информации, сборе статистических данных. (Оценить зависимость урожайности сельскохозяйственной культуры от балла экономической оценки земель по этой культуре. При этом подбирается статистика по урожайности и баллам оценки с-х культуры за последние 12-15 лет.
Слайд 102.Виды и классы моделей, применяемые в экономике.
Оптимизационная модель основана на методах
математического программирования, позволяющих находить экстемальные (максимальные или минимальные) значения целевой функции по искомому перечню переменных при заданных условиях. Например, необходимо найти такие размеры сх органицации (общая площадь, состав земельных угодий и размер отраслей), которые, исходя из его специализации, фондооснащенности и трудообеспеченности давали бы максимальную прибыль.
Слайд 112.Виды и классы моделей, применяемые в экономике.
Балансовая модель основана на взаимном
сопоставлении имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них. Под балансовой моделью следует понимать систему уравнений, которые удовлетворяют следующему требованию: соответствие наличия ресурса и его использования (модель межотраслевого баланса производства и распределения продукции в региональной экономике).
Слайд 122.Виды и классы моделей, применяемые в экономике.
Модели сетевого планирования и управления
применяются при планировании и организации землеустроительных работ, при разработке планов перехода к новому составу угодий и новым севооборотам, при составлении планов реализации проекта землеустройства и авторского надзора.
Слайд 133.Требования, предъявляемые к использованию математических методов и моделей в экономике.
Сочетание при
моделировании количественного и качественного анализа (выявление зависимостей и их математическое описание в виде систем переменных и ограничений).
Разрабатываемые модели должны учитывать экономические, технологические, технические и др. условия.
Возможности моделирования жестко связаны с качеством исходной информации.
Обязательный анализ и корректировка моделей и результатов решений.
Максимальное упрощение модели, только в таком случае, ее можно будет модифицировать.
Комплексное применение математических методов и моделей.
Разрабатываемые модели должны учитывать экономические, технологические, технические и др. условия.
Возможности моделирования жестко связаны с качеством исходной информации.
Обязательный анализ и корректировка моделей и результатов решений.
Максимальное упрощение модели, только в таком случае, ее можно будет модифицировать.
Комплексное применение математических методов и моделей.
Слайд 144.Стадии экономико-математического моделирования
Процесс решения задач подразделяется на несколько стадий:
1.
Математическая формулировка условий задач в виде систем неравенств и уравнений;
2. Решение задачи симплекс или распределительным методом;
приведение задач к канонической форме и нахождение первого варианта допустимого базисного;
решение задачи и проверка найденного варианта плана на оптимальность;
последовательное улучшение плана до получения оптимального.
3. Экономический анализ и корректировка оптимального плана.
2. Решение задачи симплекс или распределительным методом;
приведение задач к канонической форме и нахождение первого варианта допустимого базисного;
решение задачи и проверка найденного варианта плана на оптимальность;
последовательное улучшение плана до получения оптимального.
3. Экономический анализ и корректировка оптимального плана.