- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основні поняття планіметрії презентация
Содержание
- 1. Основні поняття планіметрії
- 2. Повторення курсу планіметрії Основні поняття планіметрії. Аксіоми
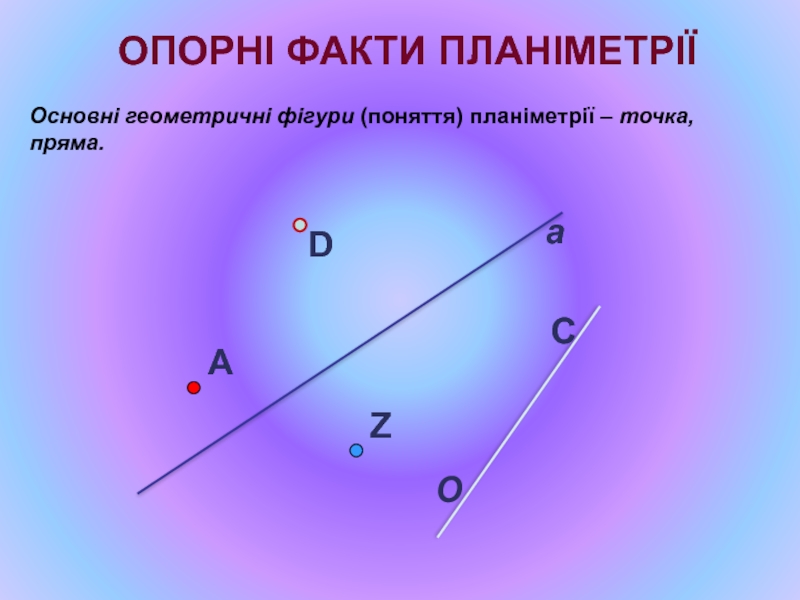
- 3. D a C O ОПОРНІ
- 4. Аксіоми планіметрії
- 9. КУТИ Два кути називаються суміжними, якщо в
- 10. Властивості паралельних прямих Якщо дві паралельні прямі
- 11. Кути в колі Якщо в колі побудувати
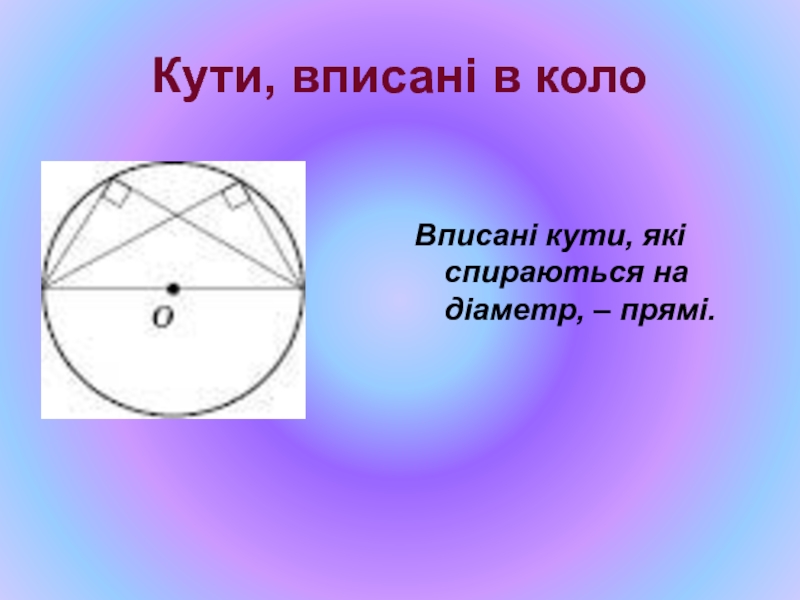
- 12. Кути, вписані в коло Вписані кути, які спираються на діаметр, – прямі.
- 13. Властивості вписаних кутів Усі вписані кути деякого
- 14. Коло і його елементи Відрізок, що сполучає
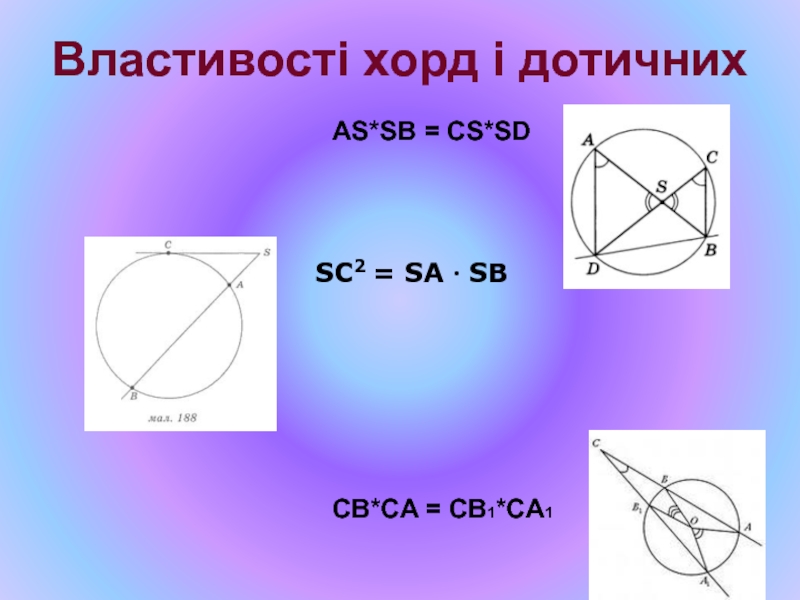
- 15. Властивості хорд і дотичних AS*SB = CS*SD
- 16. Трикутники Залежно від міри кутів, трикутники поділяють
- 17. Означення трикутника: Трикутник – це фігура, яка
- 18. Трикутники
- 19. Співвідношення сторін і кутів у прямокутному трикутнику
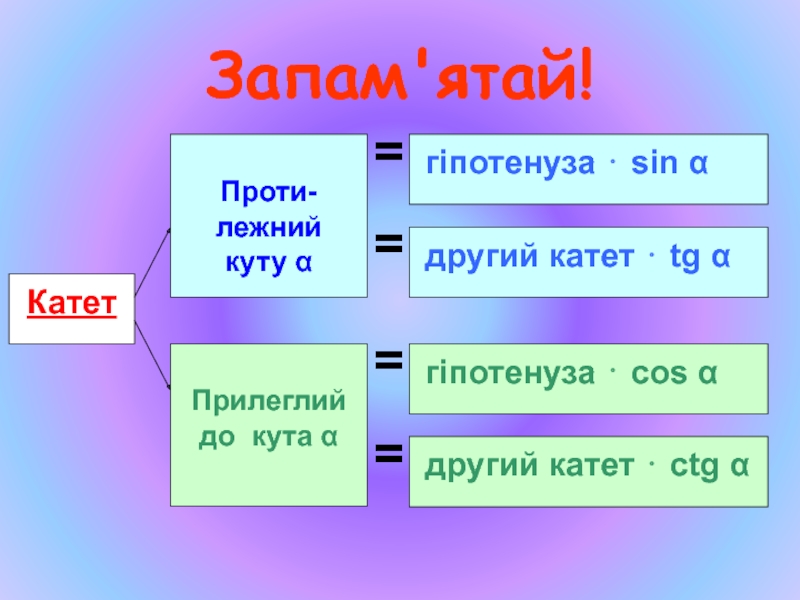
- 20. Запам'ятай!
- 21. Запам'ятай!
- 22. У прямокутному трикутнику сума квадратів катетів
- 23. Трикутники
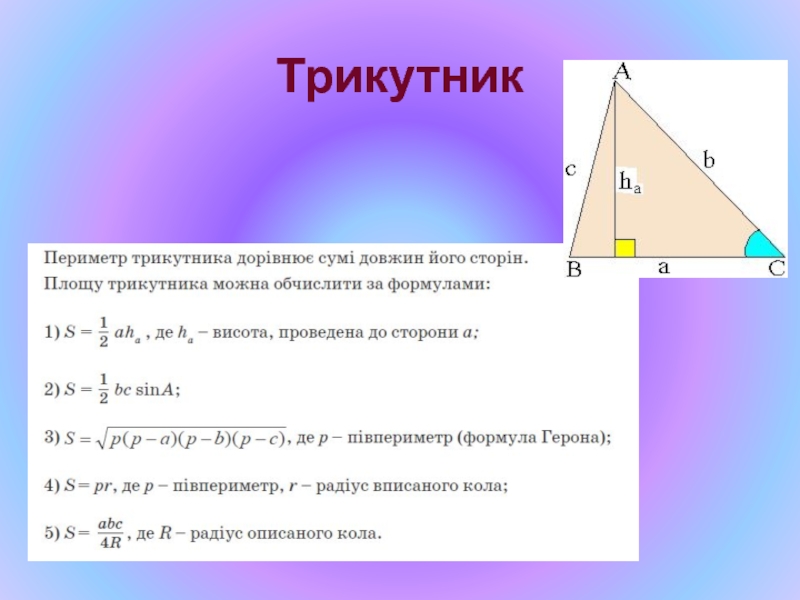
- 24. Трикутник
- 25. Ознаки рівності й ознаки подібності трикутників
- 26. Означення вписаних і описаних трикутників та їх властивості
- 27. Паралелограм Паралелограм ABCD (мал. 6): 1) AD
- 28. Прямокутник Прямокутник ABCD (мал. 7): 1) усі властивості паралелограма; 2)
- 29. Ромб
- 30. Квадрат Квадрат ABCD (мал. 9): усі властивості паралелограма, прямокутника, ромба. Площа квадрата: S = a2.
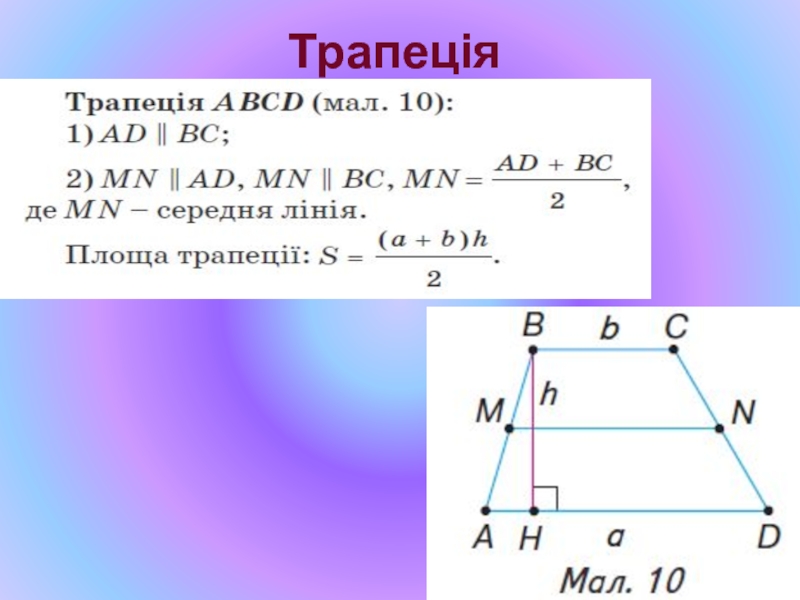
- 31. Трапеція
- 32. Правильні многокутники
- 33. Чотирикутник, всі вершини якого лежать на колі,
- 34. Властивості вписаних і описаних чотирикутників 1) у
- 35. Де знаходиться центр кола, описаного навколо
- 36. Теорема: навколо чотирикутника можна описати коло ,
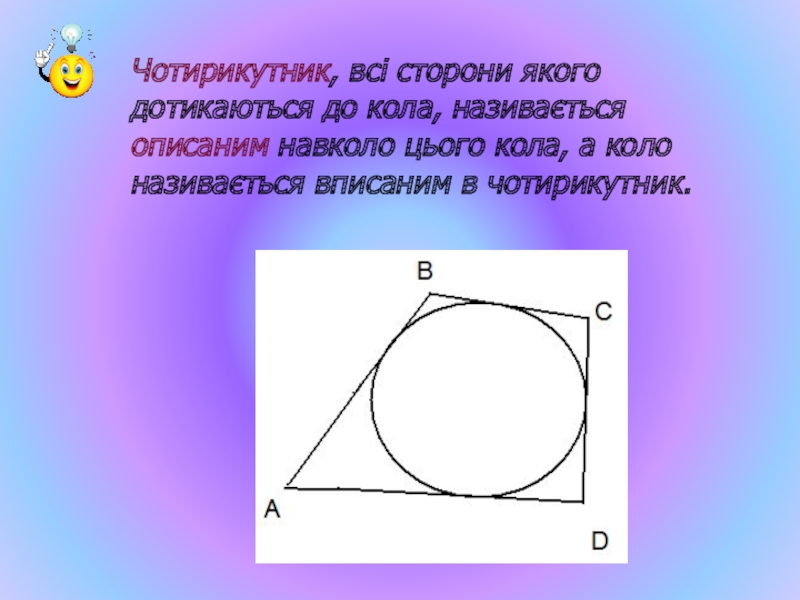
- 37. Чотирикутник, всі сторони якого дотикаються до кола,
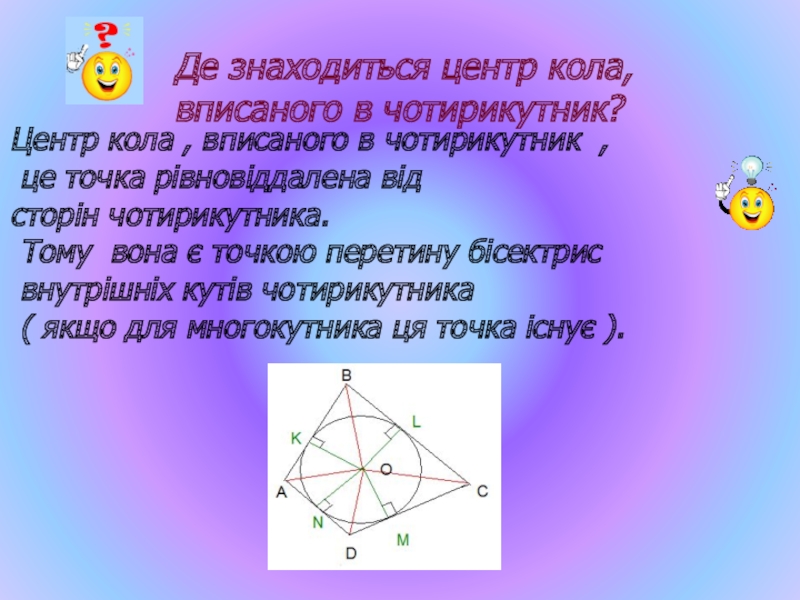
- 38. Де знаходиться центр кола, вписаного в чотирикутник?
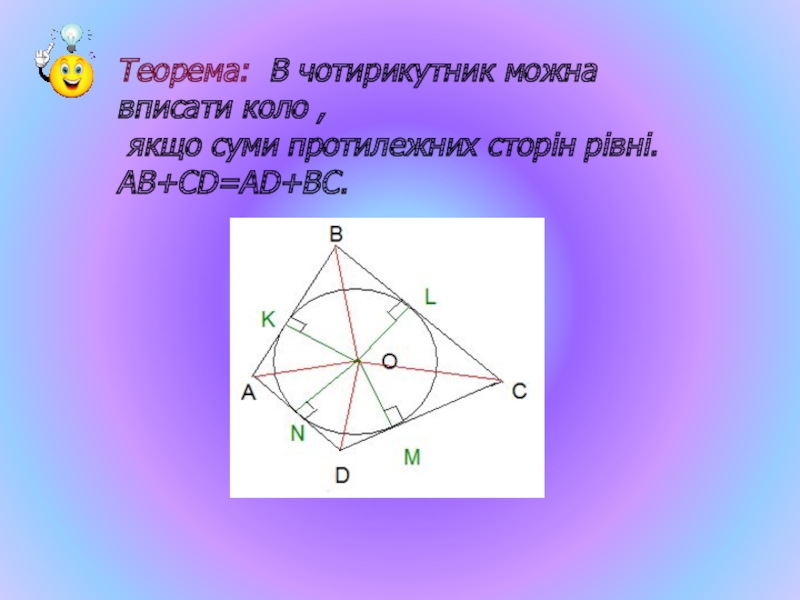
- 39. Теорема: В чотирикутник можна вписати коло ,
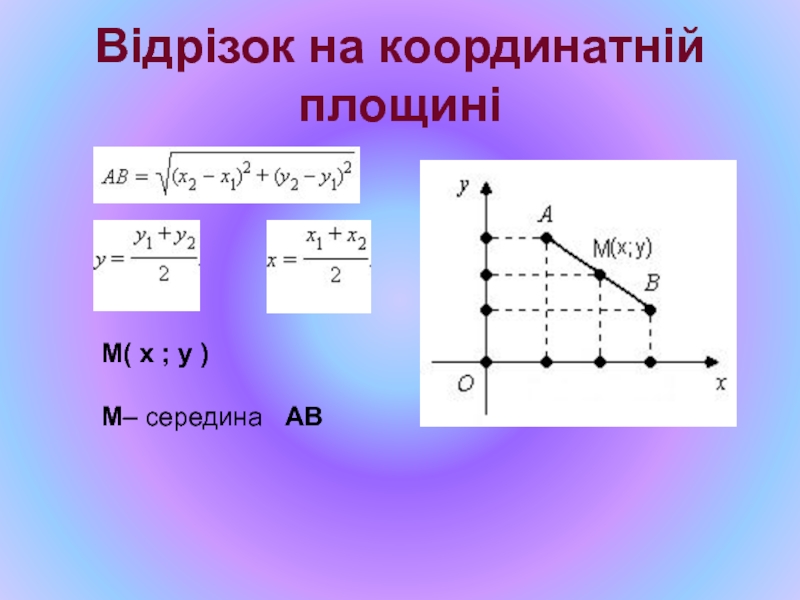
- 40. Відрізок на координатній площині M( x ; y ) M– середина AB
- 41. Рівняння кола (x – a)2 + (y – b)2 = R2 , де R >
- 42. Рівняння прямої ax + by = с, де a
- 43. ВЕКТОР. ПОЗНАЧЕННЯ ВЕКТОРА Вектором називається напрямлений відрізок,
- 44. Щоб знайти координати вектора _ а (х1;у1)
- 45. Абсолютна величина вектора обчислюється за формулою А(х1;у1) В(х2;у2) ___ ___________________ |АВ|=√(х2-х1)2+(у2-у1)2
- 46. ДІЇ З ВЕКТОРАМИ Сумою векторів
- 47. Сума двох векторів Правило трикутника
- 48. Закони додавання векторів 1) а+b=b+a (переставний закон)
- 49. МНОЖЕННЯ ВЕКТОРА НА ЧИСЛО. Добутком вектора
- 50. СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ Скалярним добутком векторів а(а1;а2)
- 51. Список використаних джерел
Слайд 2Повторення курсу планіметрії
Основні поняття планіметрії.
Аксіоми планіметрії.
Основні властивості геометричних фігур та їх
Методи розв’язування геометричних задач.
Слайд 9КУТИ
Два кути називаються суміжними, якщо в них одна сторона спільна, а
Сума суміжних кутів дорівнює 180°.
Два кути називаються вертикальними, якщо сторони одного кута є доповняльними променями сторін другого (мал. 2).
Вертикальні кути рівні.
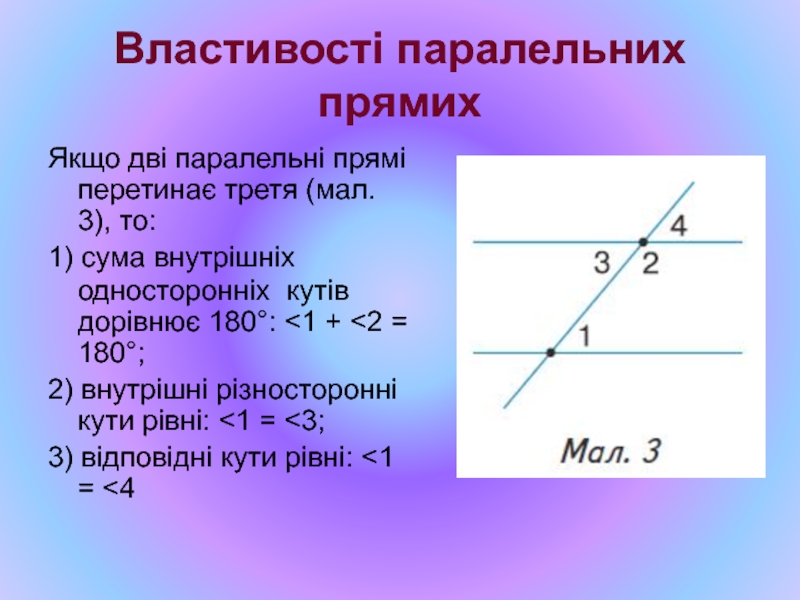
Слайд 10Властивості паралельних прямих
Якщо дві паралельні прямі перетинає третя (мал. 3), то:
1)
2) внутрішні різносторонні кути рівні: <1 = <3;
3) відповідні кути рівні: <1 = <4
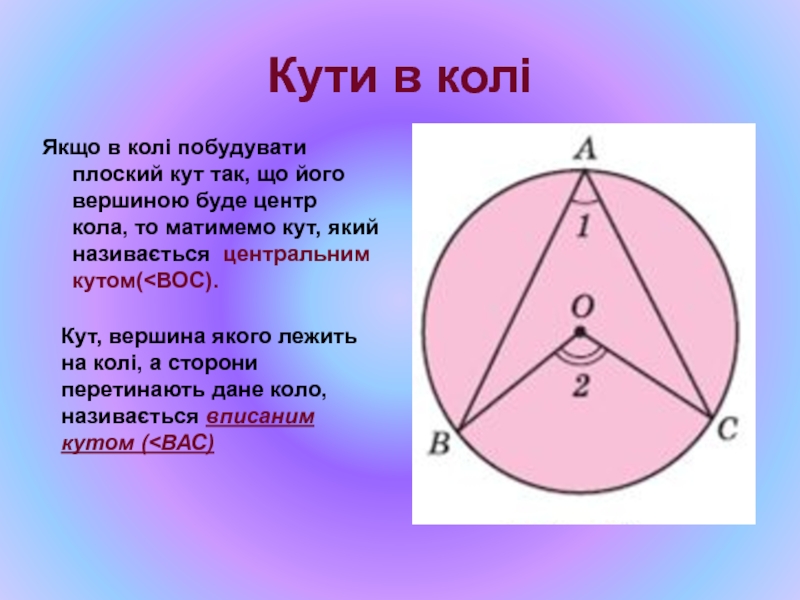
Слайд 11Кути в колі
Якщо в колі побудувати плоский кут так, що його
Кут, вершина якого лежить на колі, а сторони перетинають дане коло, називається вписаним кутом (<ВАС)
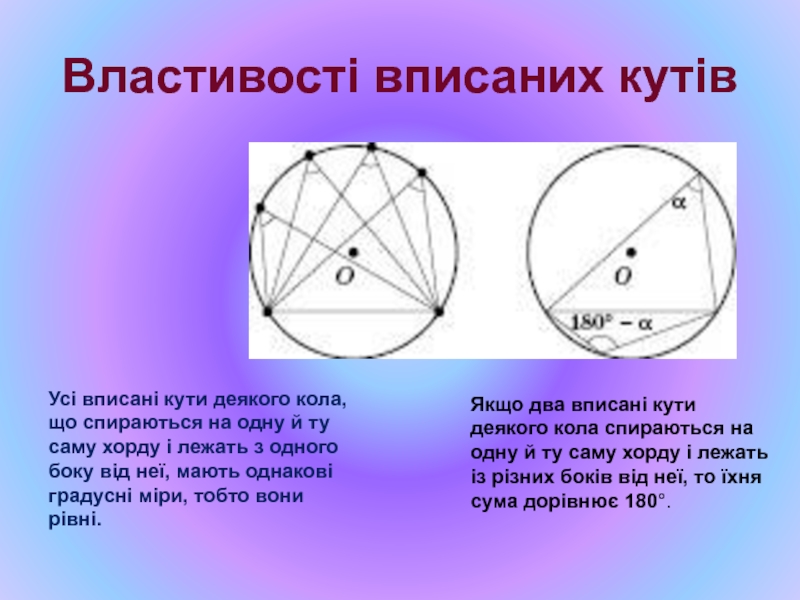
Слайд 13Властивості вписаних кутів
Усі вписані кути деякого кола, що спираються на одну
Якщо два вписані кути деякого кола спираються на одну й ту саму хорду і лежать із різних боків від неї, то їхня сума дорівнює 180°.
Слайд 14Коло і його елементи
Відрізок, що сполучає дві точки кола, називають хордою.
Хорду, що проходить через центр кола, називають діаметром.
Колом називають геометричну фігуру, яка складається з усіх точок площини, рівновіддалених від даної точки. Цю точку називають центром кола, а відрізок, що сполучає центр кола з будь-якою точкою кола, називають радіусом.
Слайд 16Трикутники
Залежно від міри кутів, трикутники поділяють на гострокутні, тупокутні й прямокутні.
Залежно
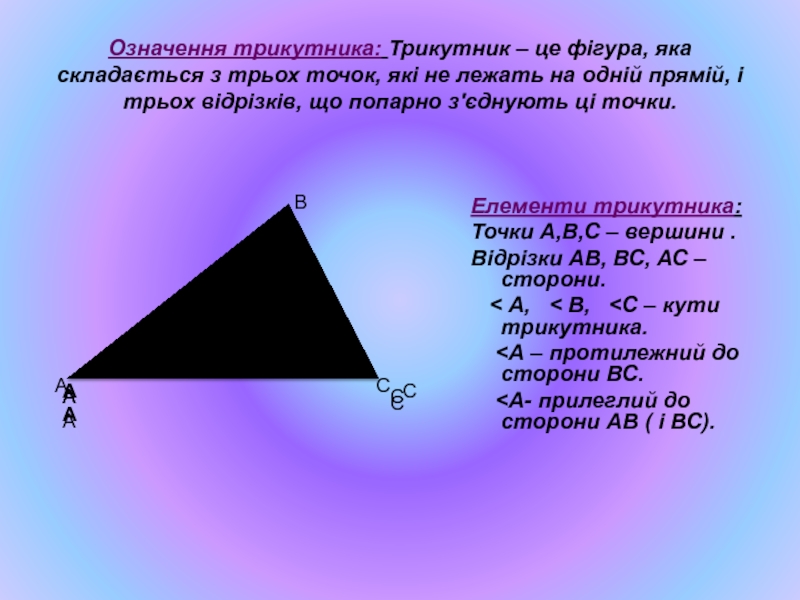
Слайд 17Означення трикутника: Трикутник – це фігура, яка складається з трьох точок,
Елементи трикутника:
Точки А,В,С – вершини .
Відрізки АВ, ВС, АС – сторони.
< А, < В, <С – кути трикутника.
<А – протилежний до сторони ВС.
<А- прилеглий до сторони АВ ( і ВС).
АА
АА
А
А
А
В
С
С
С
С
Слайд 22
У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи
Теорема Піфагора
а
c
b
а2+b2=с2
Слайд 27Паралелограм
Паралелограм ABCD (мал. 6):
1) AD || BC, AB || DC;
2) AD
3) 4) AO = OC, BO = OD;
5) < A + < B = 180°, < A + < D = 180°.
Площа паралелограма: S = ah.
Слайд 28Прямокутник
Прямокутник ABCD (мал. 7):
1) усі властивості паралелограма;
2)
Площа прямокутника: S = ab.
Слайд 30Квадрат
Квадрат ABCD (мал. 9): усі властивості паралелограма, прямокутника, ромба.
Площа квадрата: S
Слайд 33Чотирикутник, всі вершини якого лежать на колі, називається вписаним у це
Слайд 34Властивості вписаних і описаних
чотирикутників
1) у вписаному чотирикутнику MNKP
(мал. 11): < M
2) в описаному чотирикутнику ABCD
(мал. 11): AB + CD = AD + BC.
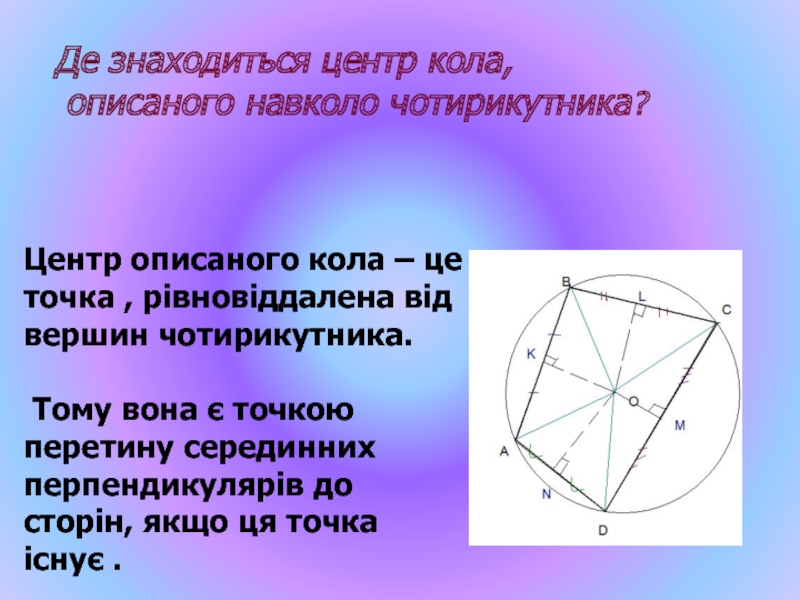
Слайд 35Де знаходиться центр кола,
описаного навколо чотирикутника?
Центр описаного кола – це
Тому вона є точкою перетину серединних перпендикулярів до сторін, якщо ця точка існує .
Слайд 36Теорема: навколо чотирикутника можна описати коло , якщо суми протилежних кутів
Кути <А і <В вписані і спираються на дуги, що доповнюють одна одну до повного кола. За теоремою про вписані кути
Слайд 37Чотирикутник, всі сторони якого дотикаються до кола, називається описаним навколо цього
Слайд 38Де знаходиться центр кола, вписаного в чотирикутник?
Центр кола , вписаного в
це точка рівновіддалена від
сторін чотирикутника.
Тому вона є точкою перетину бісектрис
внутрішніх кутів чотирикутника
( якщо для многокутника ця точка існує ).
Слайд 39Теорема: В чотирикутник можна вписати коло ,
якщо суми протилежних сторін
Слайд 41Рівняння кола
(x – a)2 + (y – b)2 = R2 , де R > 0 , є рівнянням кола
Слайд 43ВЕКТОР. ПОЗНАЧЕННЯ ВЕКТОРА
Вектором називається напрямлений відрізок, тобто відрізок, в якому виділено
Вектори позначають так: а, b, c
Або за початком і кінцем: AB, CD.
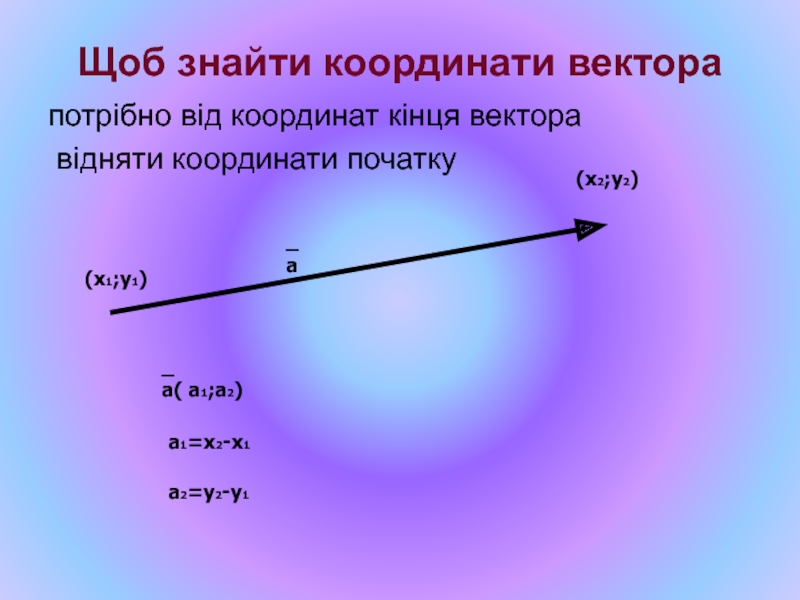
Слайд 44Щоб знайти координати вектора
_
а
(х1;у1)
(х2;у2)
_
а( а1;а2)
а1=х2-х1
а2=у2-у1
потрібно від координат
відняти координати початку
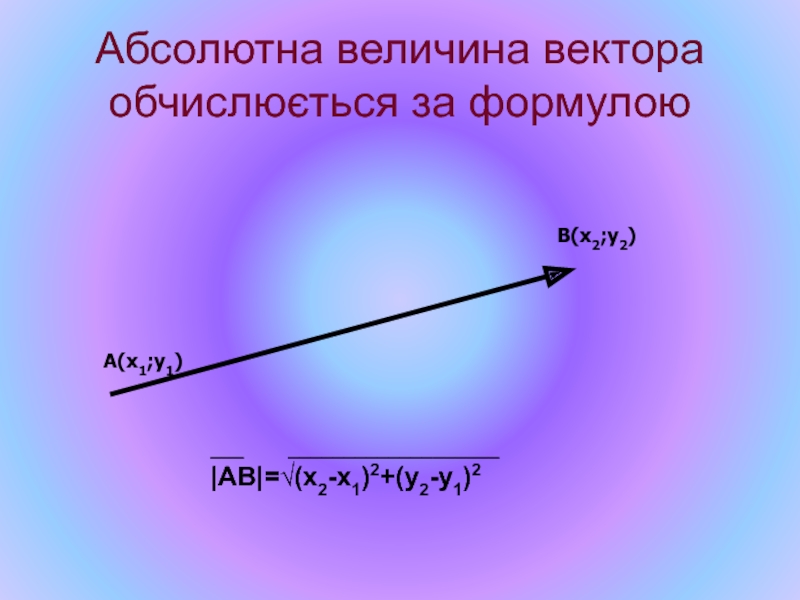
Слайд 45Абсолютна величина вектора обчислюється за формулою
А(х1;у1)
В(х2;у2)
___ ___________________
|АВ|=√(х2-х1)2+(у2-у1)2
Слайд 46
ДІЇ З ВЕКТОРАМИ
Сумою векторів а і b з координатами а1, а2
а(а1, а2 ) + b(b1, b2 ) =
= с(а1+ b1 ; а2 + b2 )
Закони додавання
а + 0 = а
а + b = b + а
а + ( b + c ) = ( a + b ) + c
c = a + b
а
b
с
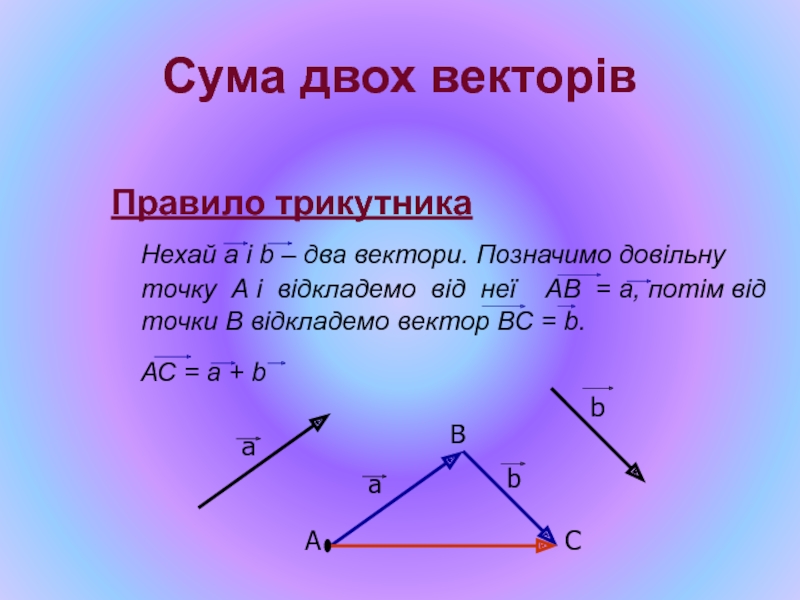
Слайд 47Сума двох векторів
Правило трикутника
Нехай а і b – два
АС = а + b
a
b
A
a
b
B
C
Слайд 48Закони додавання векторів
1) а+b=b+a (переставний закон)
Правило паралелограма
Нехай а і
АС = АВ + BС = а+b
АС = АD + DС = b+a
2) (а+b)+c=a+(b+c)
(сполучний закон)
a
a
b
b
A
D
C
B
a
b
Слайд 49МНОЖЕННЯ ВЕКТОРА НА ЧИСЛО.
Добутком вектора (а1;а2) на число λ називається вектор
(а1;а2) λ=(λа1; λа2)
Закони множення вектора на число
Для будь – якого вектора а та чисел λ, μ
(λ + μ) а = λа + μа
Для будь – яких двох векторів а і b та числа λ
λ (а + b ) = λ а +λb
Слайд 50СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ
Скалярним добутком векторів а(а1;а2) і b(b1;b2) називається число а1b1+a2b2
Якщо
а
b
β
Слайд 51Список використаних джерел
Апостолова Г.В. Геометрія: 9: дворівн. підруч. для загальноосвіт. навч.закл. – К.: Генеза, 2009.
Апостолова Г.В. Геометрія 7 кл. : підруч. для загальноосвітніх навч.закл. – К.: Генеза, 2008.
Апостолова Г.В. Геометрія 8 кл. : підруч. для загальноосвітніх навч.закл. – К.: Генеза, 2008.
Роєва Т.Г., Синельник Л.Я., Кононенко С.А. Геометрія у таблицях. 7-9 класи: Навч. посібник. – 2-ге вид., випр. і допов. –Х.: Видавнича група “Академія”, 2001. – 128 с.
ІНТЕРНЕТ-РЕСУРСИ
http://www.dgeometry.ru/links.html
http://pcmath.ru/?parent=16&page=16