- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Осевая и центральная симметрия презентация
Содержание
- 1. Осевая и центральная симметрия
- 2. Что такое симметрия «Словарь С.И. Ожегова»: «Симметрия
- 3. Вейль Герман Вейль Герман (9.11.1885— 8.12.1955) -
- 4. Виды симметрии. ОСЕВАЯ(ЗЕРКАЛЬНАЯ) СИММЕТРИЯ. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ.
- 5. Осевая (зеркальная) симметрия. Фигура называется симметричной относительно
- 6. Осевая симметрия Две точки
- 7. Фигура называется симметричной
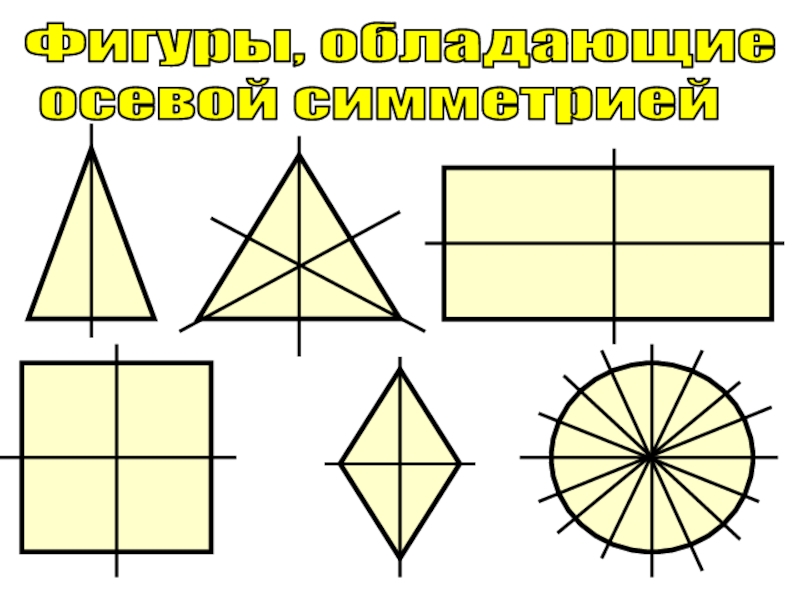
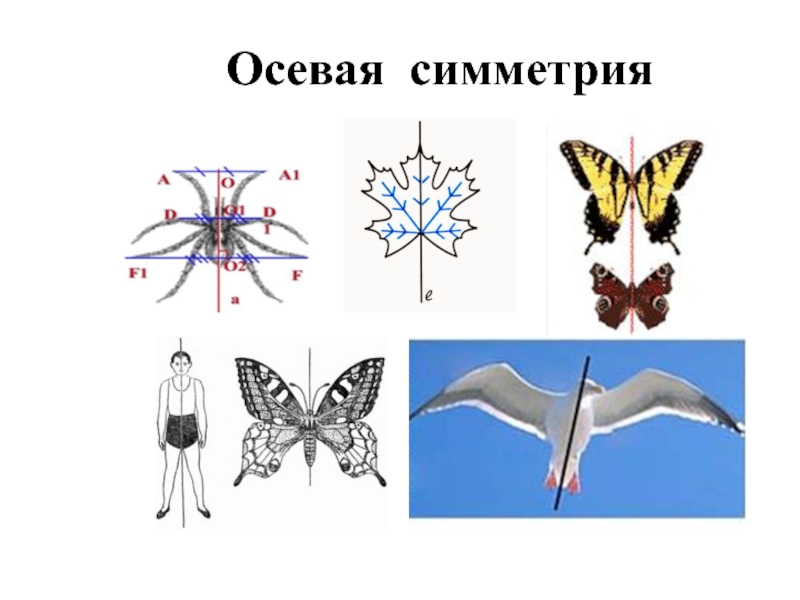
- 8. Фигуры, обладающие осевой симметрией
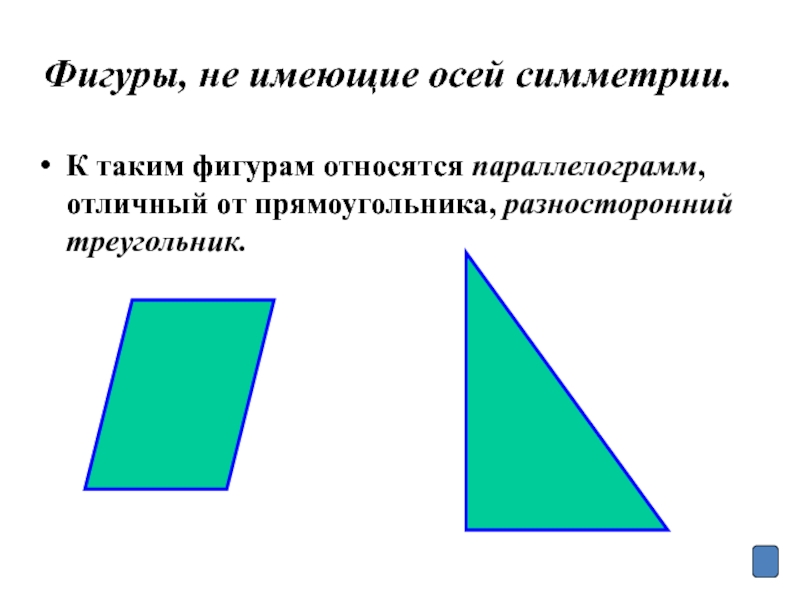
- 9. Фигуры, не имеющие осей симметрии. К таким
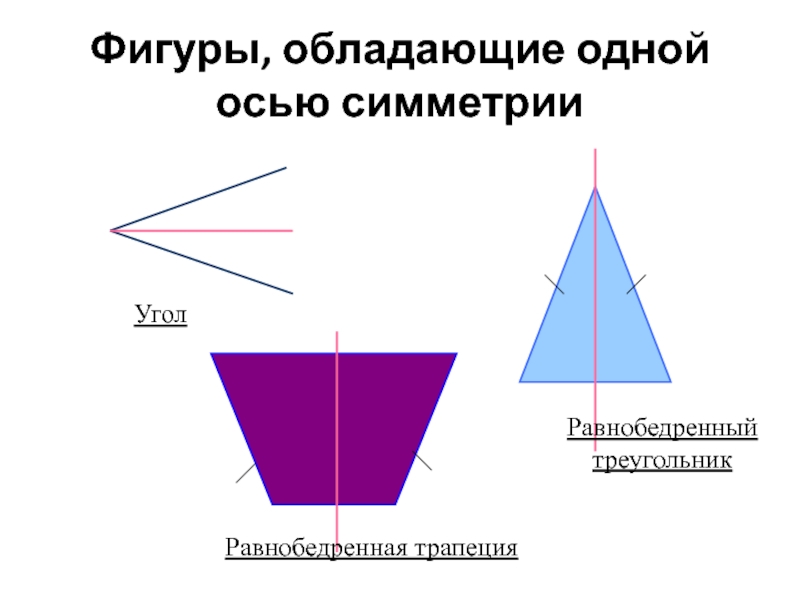
- 10. Фигуры, обладающие одной осью симметрии Угол Равнобедренный треугольник Равнобедренная трапеция
- 11. Фигуры, обладающие двумя осями симметрии Прямоугольник Ромб
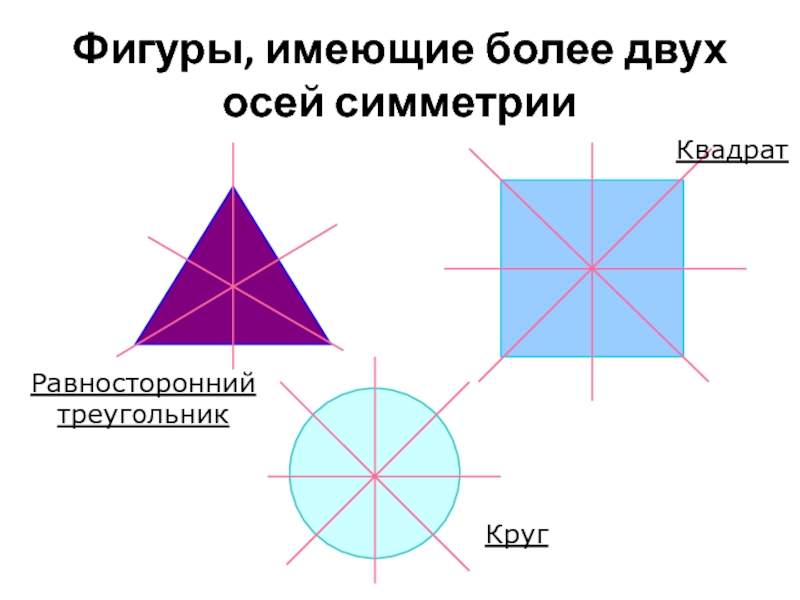
- 12. Фигуры, имеющие более двух осей симметрии Равносторонний треугольник Квадрат Круг
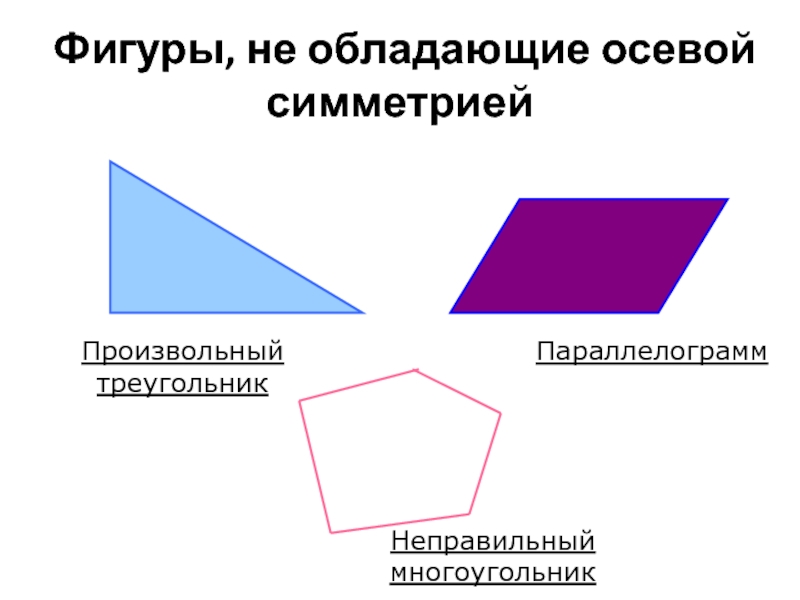
- 13. Фигуры, не обладающие осевой симметрией Произвольный треугольник Параллелограмм Неправильный многоугольник
- 14. В Е Ж З К Н О
- 15. А Д Ж Л М Н О
- 16. Б Г И Р У Ц Ч Я Щ Буквы без оси симметрии
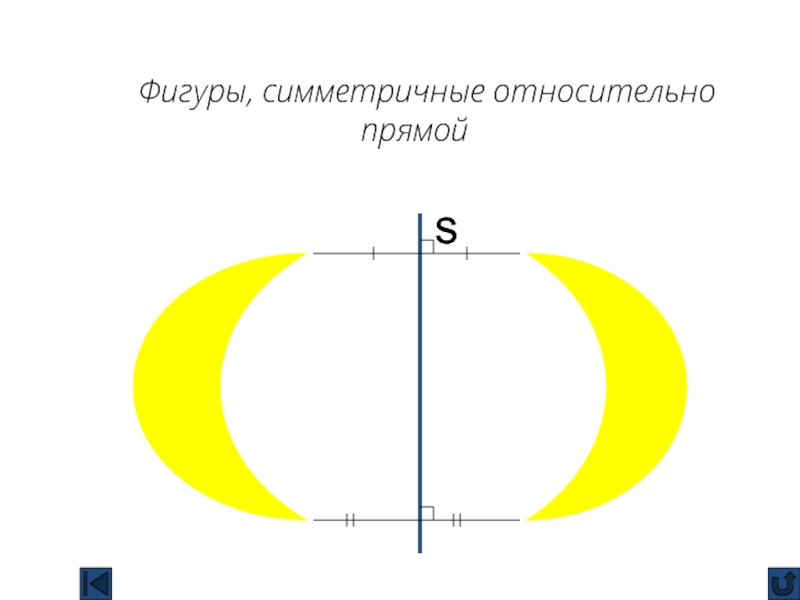
- 17. Фигуры, симметричные относительно прямой s
- 18. Осевая симметрия
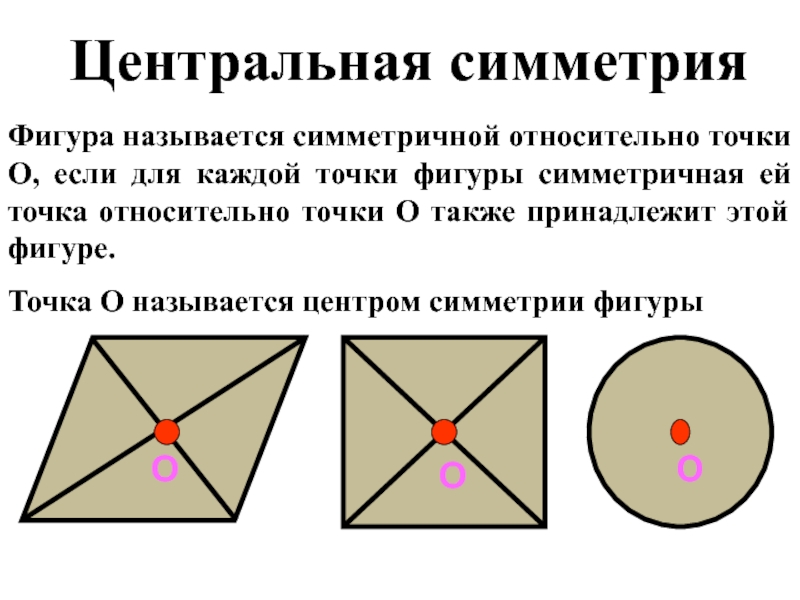
- 19. Фигура называется симметричной относительно точки О, если
- 20. Центральная симметрия. Фигура называется симметричной относительно
- 21. Фигуры, обладающие центральной симметрией. Примерами фигур, обладающих
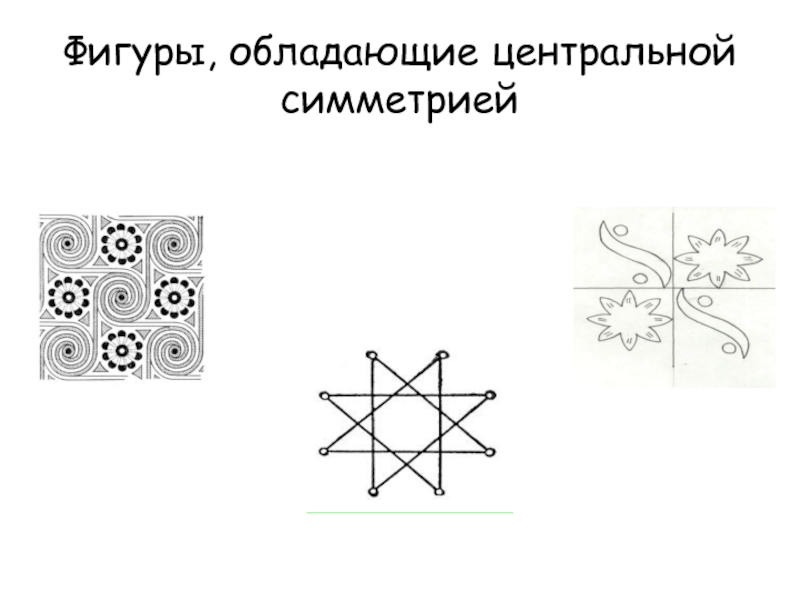
- 22. Фигуры, обладающие центральной симметрией
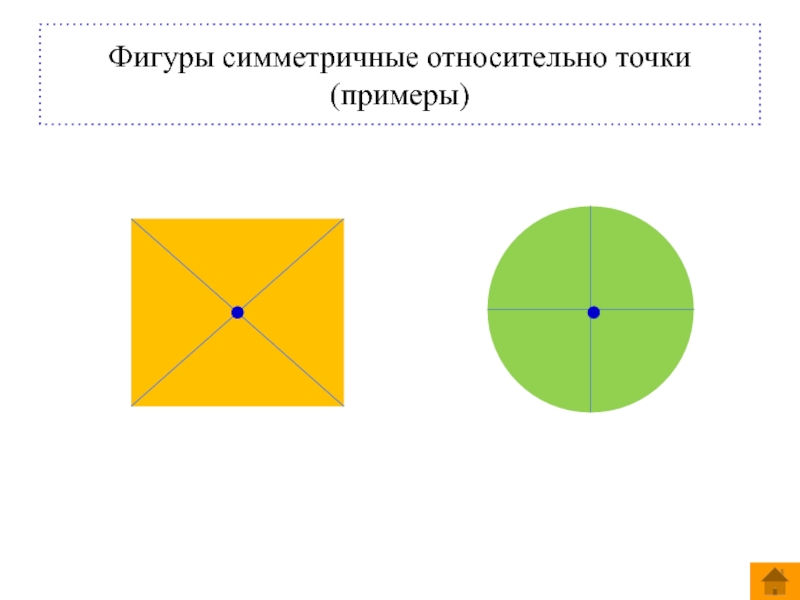
- 23. Фигуры симметричные относительно точки (примеры)
- 24. Какие из букв А, Б, Г,
- 25. Пример центральной симметрии
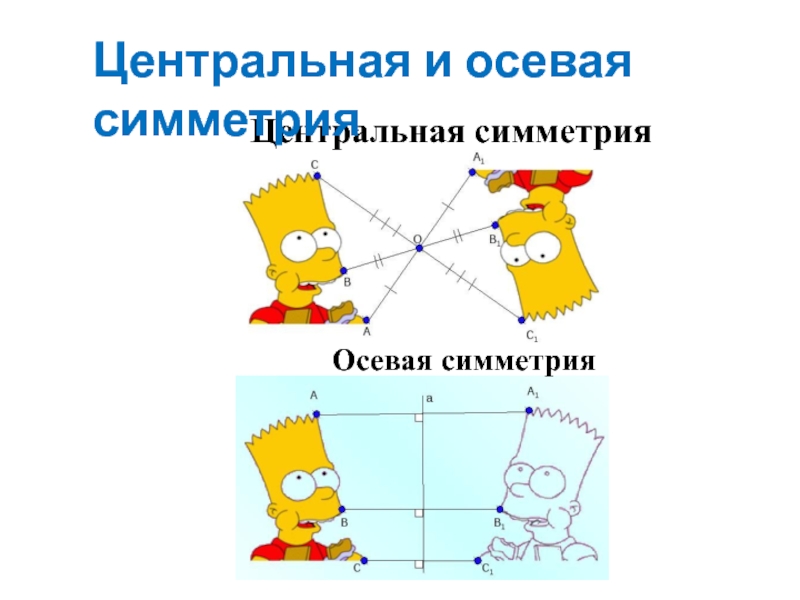
- 26. Центральная симметрия Осевая симметрия Центральная и осевая симметрия
Что такое симметрия «Словарь С.И. Ожегова»: «Симметрия - соразмерность, пропорциональность частей чего-нибудь, расположенных по обе стороны от середины, центра». «Словарь иностранных слов»: «Симметрия – полное зеркальное соответствие в расположении частей
Слайд 2Что такое симметрия
«Словарь С.И. Ожегова»: «Симметрия - соразмерность, пропорциональность частей чего-нибудь,
расположенных по обе стороны от середины, центра».
«Словарь иностранных слов»: «Симметрия – полное зеркальное соответствие в расположении частей целого относительно средней линии, центра; соразмерность».
«Словарь иностранных слов»: «Симметрия – полное зеркальное соответствие в расположении частей целого относительно средней линии, центра; соразмерность».
Слайд 3Вейль Герман
Вейль Герман (9.11.1885— 8.12.1955) - немецкий математик. Окончил Гёттингенский университ.
В 1913—1930г. профессор Цюрихского политехнического института, в 1930—33 профессор Гёттингенского университета, в 1933 эмигрировал в США.
Слайд 5Осевая (зеркальная) симметрия.
Фигура называется симметричной относительно прямой а, если для каждой
точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
Слайд 6 Осевая симметрия
Две точки А и А1 называются симметричными
относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
•
•
А
А1
а
Слайд 7 Фигура называется симметричной относительно прямой а, если
для каждой точки фигуры, симметричная ей точка относительно прямой а также принадлежит этой фигуре.
а
а - ось симметрии
Осевая симметрия
•
•
А
А1
Слайд 9Фигуры, не имеющие осей симметрии.
К таким фигурам относятся параллелограмм, отличный от
прямоугольника, разносторонний треугольник.
Слайд 10Фигуры, обладающие одной осью симметрии
Угол
Равнобедренный
треугольник
Равнобедренная трапеция
Слайд 13Фигуры, не обладающие осевой симметрией
Произвольный треугольник
Параллелограмм
Неправильный многоугольник
Слайд 19Фигура называется симметричной относительно точки О, если для каждой точки фигуры
симметричная ей точка относительно точки О также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры.
Точка О называется центром симметрии фигуры.
Центральная симметрия
О
О
О
Слайд 20Центральная симметрия.
Фигура называется симметричной относительно точки О, если для каждой точки
фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
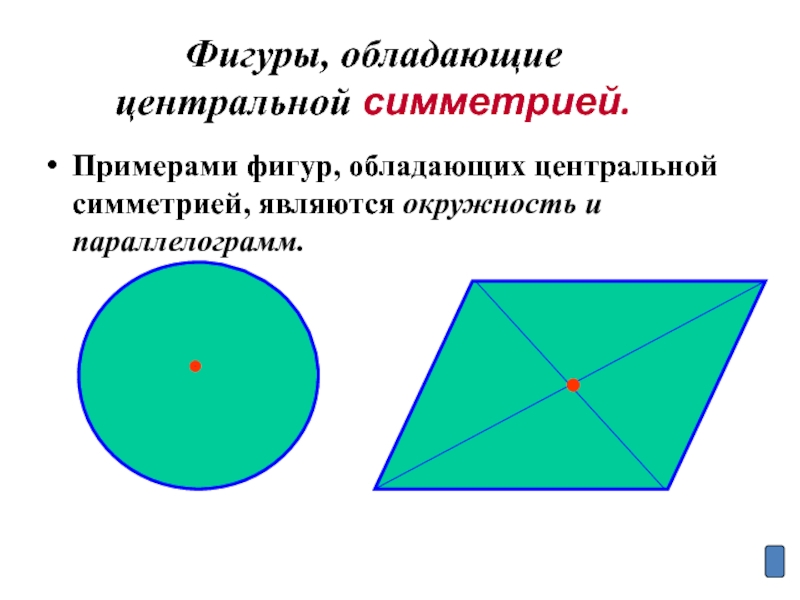
Слайд 21Фигуры, обладающие центральной симметрией.
Примерами фигур, обладающих центральной симметрией, являются окружность и
параллелограмм.
Слайд 24Какие из букв А, Б, Г, Е, Х, И, М, Н,
О, Т, Я имеют:
а) центр симметрии
Х, И, Н, О
б) ось симметрии
А, Е, Х, М, Н, О, Т
Слайд 27
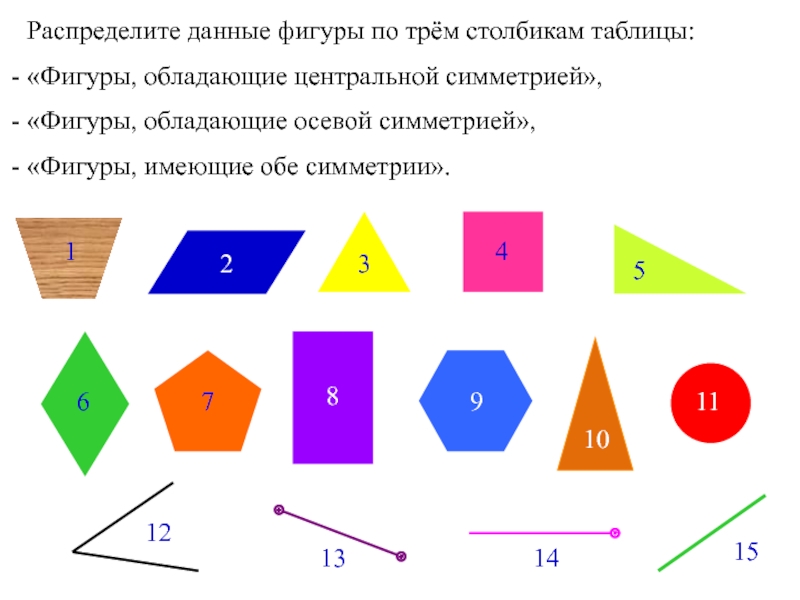
Распределите данные фигуры по трём столбикам таблицы:
«Фигуры, обладающие центральной
симметрией»,
«Фигуры, обладающие осевой симметрией»,
«Фигуры, имеющие обе симметрии».
«Фигуры, обладающие осевой симметрией»,
«Фигуры, имеющие обе симметрии».
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
