- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определители матриц. Обратная матрица, ранг матрицы презентация
Содержание
- 1. Определители матриц. Обратная матрица, ранг матрицы
- 2. Определители.( детерминанты). (Детерминанты квадратных матриц 2-го
- 3. Определение Детерминантом (или определителем) квадратной матрицы 2-го порядка называется число .
- 4. Определение Детерминантом (или определителем) квадратной матрицы 3-го порядка называется число:
- 5. Теорема Определитель матрицы 3-го порядка может быть
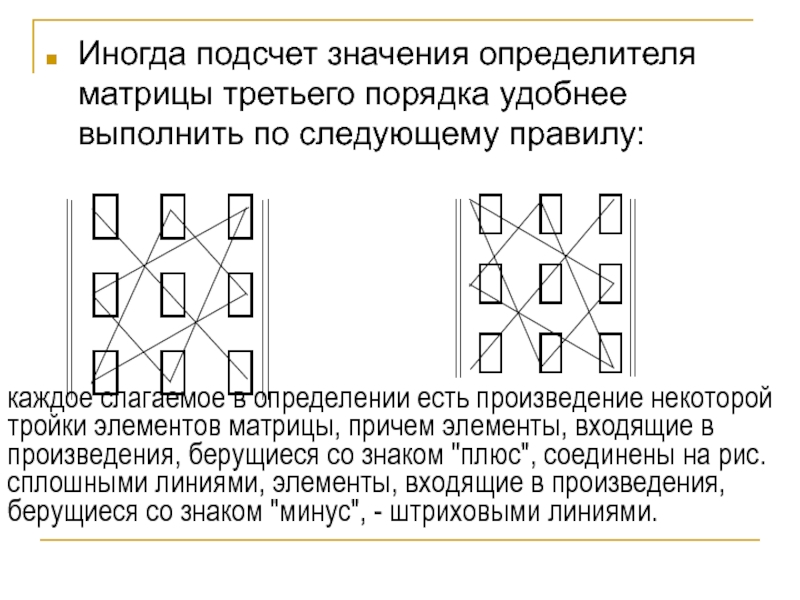
- 6. Иногда подсчет значения определителя матрицы третьего порядка
- 7. Рассмотрим множество, состоящее из натуральных чисел .
- 8. Определение: Будем говорить, что числа ki и
- 9. Пусть дана квадратная матрица
- 10. Определение: Детерминантом (или определителем) квадратной матрицы
- 11. Определение. Дополнительным Мij минором произвольного элемента квадратной
- 12. Замечание: Поскольку в данном определении указано, что
- 13. Формула для вычисления определителей: det A
- 14. Вообще говоря, определитель может вычисляться по любой
- 15. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ: Свойство1. det A =
- 16. Свойство 4. При умножении столбца (или строки)
- 17. Свойство 5. Если в матрице А строки
- 18. Свойство 7. Определитель матрицы не изменится, если
- 19. Свойство 8. Если для элементов какой-
- 20. ОБРАТНАЯ МАТРИЦА (Нахождение и применение)
- 21. Обратная матрица Определение. Если существуют квадратные
- 22. Матрица , для которой
- 23. Нахождение обратной матрицы 1) Рассмотрим общий подход
- 24. Таким образом, получаем систему уравнений:
- 25. 2) При нахождении обратных матриц обычно применяют
- 26. 3) К матрице Aij «дописывают» справа единичную
- 27. Элементарные преобразования матрицы Определение. Элементарными преобразованиями
- 28. Те же операции, применяемые для столбцов, также
- 29. Cвойства обратных матриц (A-1)-1 = A;
- 30. ПРИМЕНЕНИЕ ОБРАТНОЙ МАТРИЦЫ обратная матрица позволяет найти решения следующих матричных уравнений: АХ=С ХВ=С АХВ=С Решение: Х=А-1С Х=СВ-1 Х=А-1СВ-1
- 31. Ранг матрицы. Определение. Минором матрицы порядка s
- 32. Определение. В матрице порядка m×n минор порядка
- 33. Определение. Порядок базисного минора матрицы называется рангом
- 34. Теорема о базисном миноре Теорема. В
- 35. Пример. Определить ранг матрицы
- 36. Если с помощью элементарных преобразований не удается
Определители.( детерминанты).
(Детерминанты квадратных матриц 2-го и 3-го порядка) Для квадратных матриц существует специальная числовая характеристика, называемая детерминантом (или определителем). Рассмотрим для начала определители квадратных матриц 2-го и 3-го
Слайд 2Определители.( детерминанты).
(Детерминанты квадратных матриц 2-го и 3-го порядка)
Для квадратных матриц
существует специальная числовая характеристика, называемая детерминантом (или определителем).
Рассмотрим для начала определители квадратных матриц 2-го и 3-го порядков.
Рассмотрим для начала определители квадратных матриц 2-го и 3-го порядков.
Слайд 3Определение
Детерминантом (или определителем) квадратной матрицы 2-го порядка называется число .
Слайд 4Определение
Детерминантом (или определителем) квадратной матрицы 3-го порядка называется число:
Слайд 5Теорема
Определитель матрицы 3-го порядка может быть выражен через определители 2-го порядка
формулой следующего вида:
разложение определителя по первой строке.
Слайд 6Иногда подсчет значения определителя матрицы третьего порядка удобнее выполнить по следующему
правилу:
каждое слагаемое в определении есть произведение некоторой тройки элементов матрицы, причем элементы, входящие в произведения, берущиеся со знаком "плюс", соединены на рис. сплошными линиями, элементы, входящие в произведения, берущиеся со знаком "минус", - штриховыми линиями.
Слайд 7Рассмотрим множество, состоящее из натуральных чисел . Будем обозначать перестановки этих
чисел (то есть последовательную их запись в некотором порядке без повторений) как
( полное число таких различных перестановок равно n!).
( полное число таких различных перестановок равно n!).
Определители высших порядков, вычисление и свойства.
Слайд 8Определение: Будем говорить, что числа ki и kj образуют в перестановке
беспорядок (нарушение порядка, или инверсию), если при i>j имеет место kiПолное число беспорядков в перестановке
будем обозначать
Например,
будем обозначать
Например,
Слайд 10Определение:
Детерминантом (или определителем) квадратной матрицы размера nxn называется число
, получаемое по формуле
где - всевозможные различные перестановки, образованные из номеров столбцов матрицы
где - всевозможные различные перестановки, образованные из номеров столбцов матрицы
Слайд 11Определение. Дополнительным Мij минором произвольного элемента квадратной матрицы aij называется определитель
матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
Определение. Алгебраическим дополнением элемента аij матрицы называется число Аij=(-1)i+jМij
Определение. Алгебраическим дополнением элемента аij матрицы называется число Аij=(-1)i+jМij
Слайд 12Замечание:
Поскольку в данном определении указано, что сумма берется по всем возможным
различным перестановкам, то число слагаемых равно n!.
Из определения также вытекает, что каждое слагаемое содержит в качестве сомножителя по одному элементу матрицы из каждого столбца и каждой строки.
Из определения также вытекает, что каждое слагаемое содержит в качестве сомножителя по одному элементу матрицы из каждого столбца и каждой строки.
Слайд 13Формула для вычисления определителей:
det A =
где М1к–дополнительный минор
элемента а1к.
(Заметим, что определители имеют только квадратные матрицы.)
(Заметим, что определители имеют только квадратные матрицы.)
Слайд 14Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы,
т.е. справедлива формула:
detA = i = 1,2,…,n.
Заметим, что:
различные матрицы могут иметь одинаковые определители;
определитель единичной матрицы равен 1.
detA = i = 1,2,…,n.
Заметим, что:
различные матрицы могут иметь одинаковые определители;
определитель единичной матрицы равен 1.
Слайд 15СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ:
Свойство1. det A = det AT;
Свойство 2. det (AB) = detA⋅detB
Свойство 3. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
Слайд 16Свойство 4. При умножении столбца (или строки) матрицы на число ее
определитель умножается на это число.
Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Слайд 17Свойство 5. Если в матрице А строки или столбцы линейно зависимы,
то ее определитель равен нулю.
Свойство 6. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 6. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Слайд 18Свойство 7. Определитель матрицы не изменится, если к элементам одной из
его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
Слайд 19
Свойство 8. Если для элементов какой- либо строки или столбца матрицы
верно соотношение:
d = d1 ± d2 , e = e1 ± e2 , f = f1 ± f2 , то верно:
d = d1 ± d2 , e = e1 ± e2 , f = f1 ± f2 , то верно:
Слайд 21Обратная матрица
Определение. Если существуют квадратные матрицы Х и А одного
порядка, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну
Слайд 23Нахождение обратной матрицы
1) Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из
определения произведения матриц, можно записать:
AX = E ⇒ , i=(1,n), j=(1,n),
eij = 0, i ≠ j,
eij = 1, i = j .
AX = E ⇒ , i=(1,n), j=(1,n),
eij = 0, i ≠ j,
eij = 1, i = j .
Слайд 252) При нахождении обратных матриц обычно применяют следующую формулу:
где xij –
соответствующий элемент обратной матрицы
M ij - дополнительный минор произвольного элемента квадратной матрицы aij , он равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
M ij - дополнительный минор произвольного элемента квадратной матрицы aij , он равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
Слайд 263) К матрице Aij «дописывают» справа единичную матрицу. С помощью элементарных
преобразований приводят матрицу Aij к единичному виду, тогда матица, которая получится справа – обратная
Слайд 27Элементарные преобразования матрицы
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение
строки на число, отличное от нуля;
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование.
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование.
Слайд 28Те же операции, применяемые для столбцов, также называются элементарными преобразованиями.
С помощью
элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк ( столбцов ).
Слайд 30ПРИМЕНЕНИЕ ОБРАТНОЙ МАТРИЦЫ
обратная матрица позволяет найти решения следующих матричных уравнений:
АХ=С ХВ=С АХВ=С
Решение:
Х=А-1С Х=СВ-1 Х=А-1СВ-1
Слайд 31Ранг матрицы.
Определение. Минором матрицы порядка s называется определитель матрицы, образованной из
элементов исходной матрицы, находящихся на пересечении каких - либо выбранных s строк и s столбцов
Слайд 32Определение. В матрице порядка m×n минор порядка r называется базисным, если
он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.
Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.
В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.
В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Слайд 33Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg
А.
Элементарные преобразования матриц не изменяют ранг матрицы
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
(Равные матрицы и эвивалентные матрицы - понятия совершенно различные)
Элементарные преобразования матриц не изменяют ранг матрицы
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
(Равные матрицы и эвивалентные матрицы - понятия совершенно различные)
Слайд 34Теорема о базисном миноре
Теорема. В произвольной матрице А каждый столбец
(строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.
Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.
Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.
Слайд 36Если с помощью элементарных преобразований не удается найти матрицу, эквивалентную исходной,
но меньшего размера, то нахождение ранга матрицы следует начинать с вычисления миноров наивысшего возможного порядка. В вышеприведенном примере – это миноры порядка 2. Если хотя бы один из них не равен нулю, то ранг матрицы равен порядку этого минора.
