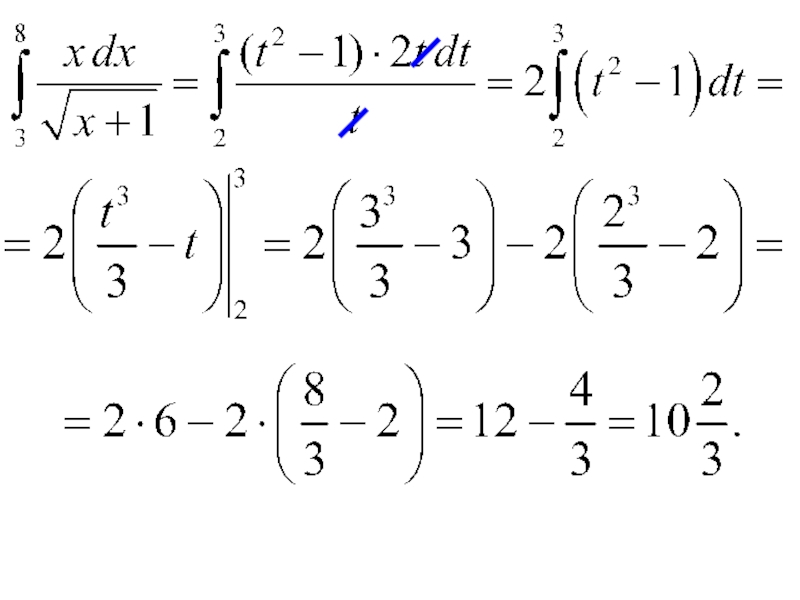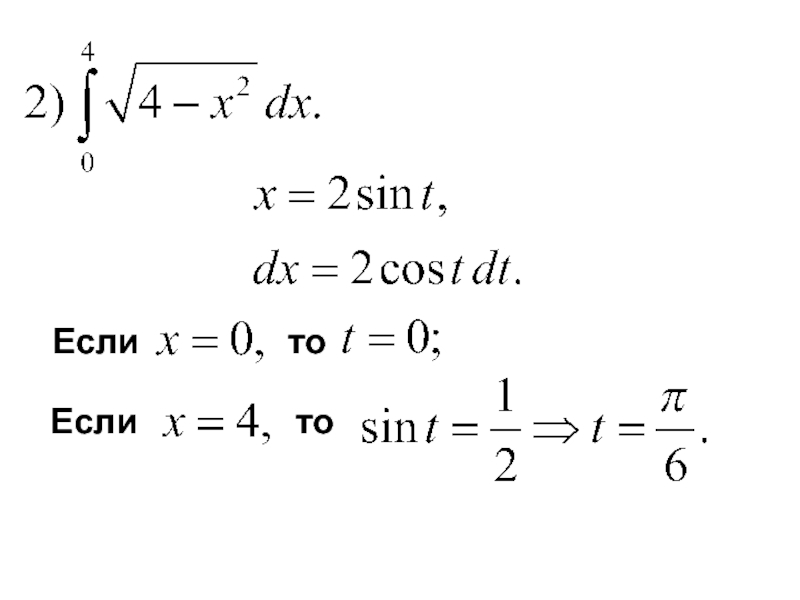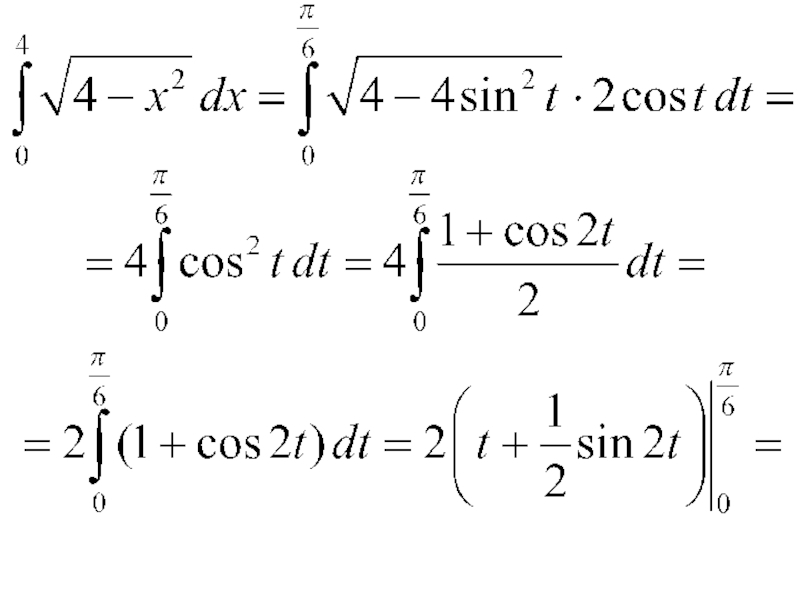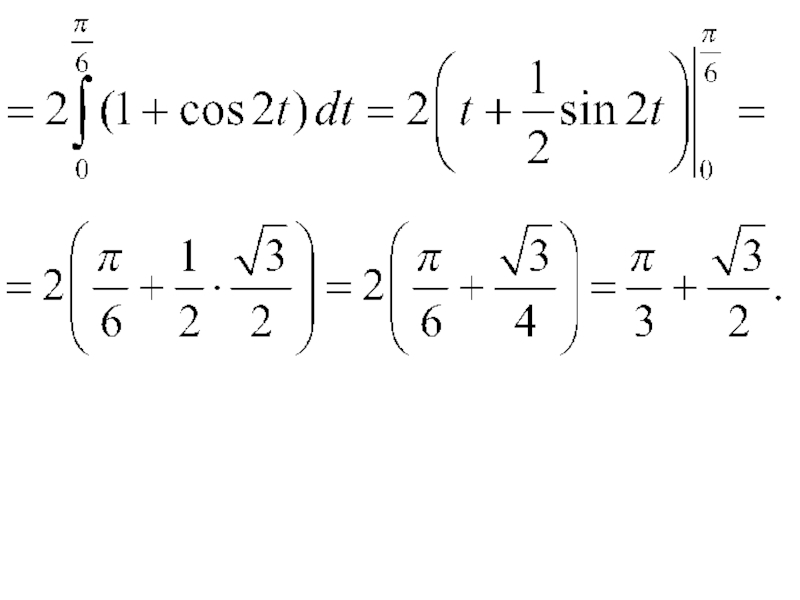- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определенный интеграл презентация
Содержание
- 1. Определенный интеграл
- 2. Рассмотрим фигуру, ограниченную слева и справа прямыми
- 3. 1) Разобьем отрезок
- 4. 2) В каждом из отрезков возьмем произвольную
- 5. 4) Назовем определенным интегралом и обозначим
- 6. Произведение
- 8. Геометрический смысл определенного интеграла: (предполагается, что
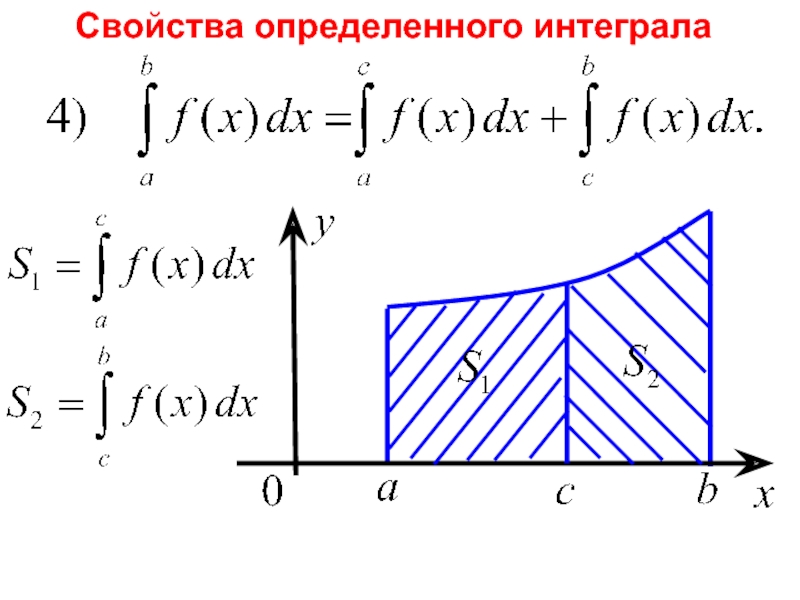
- 9. Свойства определенного интеграла
- 10. Свойства определенного интеграла
- 11. Свойства определенного интеграла
- 12. Теорема о среднем значении Если
- 13. Формула Ньютона-Лейбница И. Ньютон (1642-1727) – великий
- 14. Примеры Предполагается, что - непрерывная функция.
- 15. Замена переменной в определенном интеграле Замена: Новые пределы интегрирования:
- 17. Если
- 20. Самостоятельная работа №1
- 21. Работы собирают старосты 9) Найти производную функции
Рассмотрим фигуру, ограниченную слева и справа прямыми и снизу отрезком оси и сверху кривой Задача о
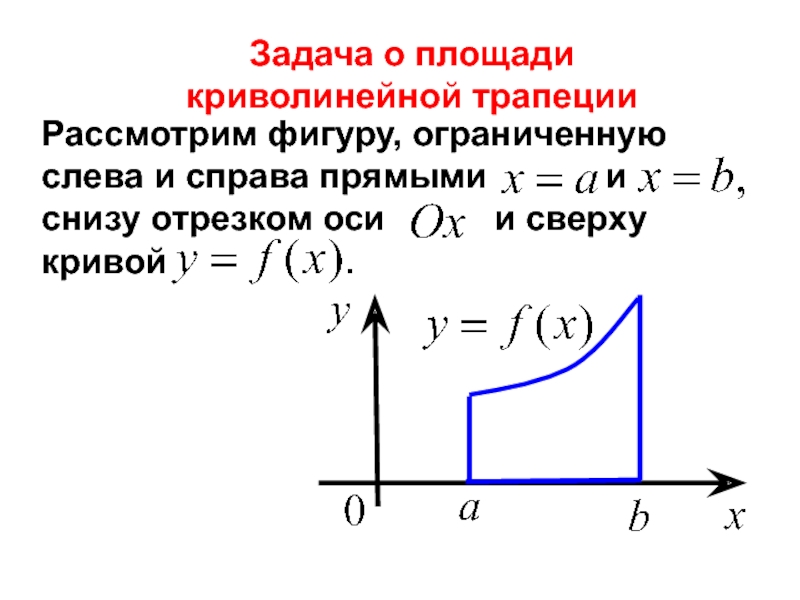
Слайд 2Рассмотрим фигуру, ограниченную слева и справа прямыми
и снизу отрезком оси и сверху кривой
Задача о площади
криволинейной трапеции
Слайд 31) Разобьем отрезок на
малых отрезков с помощью точек деления
Такая фигура называется криволинейной трапецией. Вычислим площадь этой фигуры.
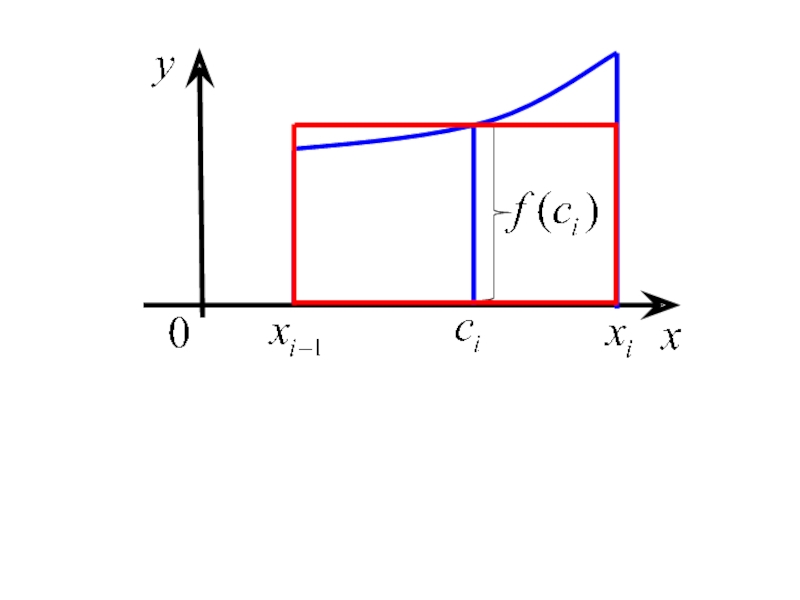
Слайд 42) В каждом из отрезков возьмем произвольную точку
где
3) Составим сумму
Назовем её интегральной суммой.
Слайд 6Произведение
численно равно площади прямоугольника с основанием и высотой
Числа и называют верхним и нижним пределами интегрирования.
- подынтегральная функция.
- подынтегральное выражение.
Слайд 13Формула Ньютона-Лейбница
И. Ньютон (1642-1727) – великий английский математик
Г. Лейбниц (1646-1716) –
великий немецкий математик.
