- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определение длины отрезка прямой линии и углов наклона проекций презентация
Содержание
- 16. Пересечение прямой с плоскостью общего положения. Пример
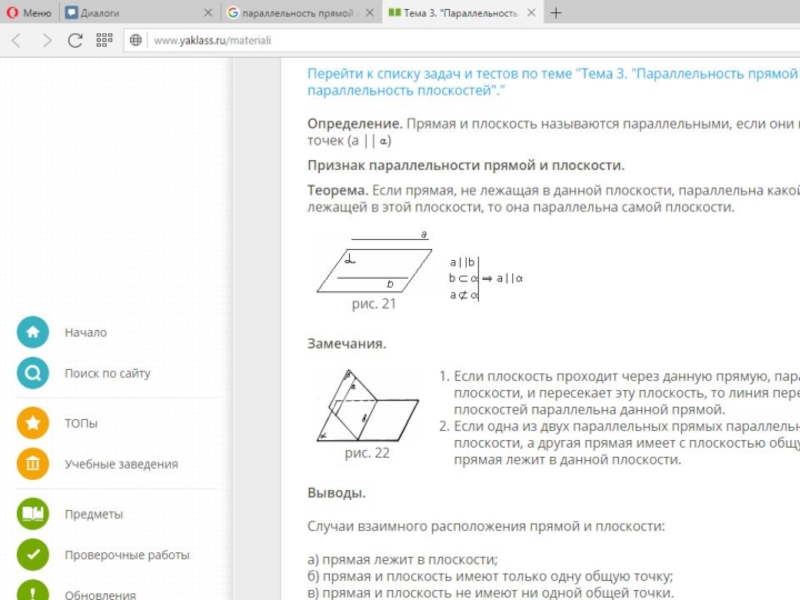
- 18. 2. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
- 19. Способ замены плоскостей проекций Сущность этого
- 20. Рассмотрим решение четырех исходных задач способом замены
- 21. 2. Преобразовать чертеж прямой уровня так, чтобы
- 24. Преобразовать комплексный чертеж так, чтобы линия общего
- 26. Построения на комплексном чертеже: 1)
- 28. 8.12. Сечение многогранника плоскостью частного положения При
- 30. Главный вид должен содержать наибольшую информацию о предмете.
- 31. Местный вид. Кроме основных видов, на чертежах используют
- 33. Наложенная проекция — изображение части предмета, находящейся
Слайд 16Пересечение прямой с плоскостью общего положения. Пример 1. Даны: плоскость общего положения а
Слайд 19Способ замены плоскостей проекций
Сущность этого способа заключается в том, что заменяют
Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.
Слайд 20Рассмотрим решение четырех исходных задач способом замены плоскостей проекций.
1. Преобразовать чертеж
Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П4, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций, т. е. от системы плоскостей П1_|_П2 перейти к системе П4 _|_ П1 или П4 _|_ П2. На чертеже новая ось проекций должна быть параллельна одной из основных проекций прямой. На рис. 108 построено изображение прямой l (А, В) общего положения в системе плоскостей П1 _|_ П4, причем П4 || l. Новые линии связи A1A4 и В1В4проведены
перпендикулярно новой оси —П1/П4 параллельной горизонтальной проекции l1.
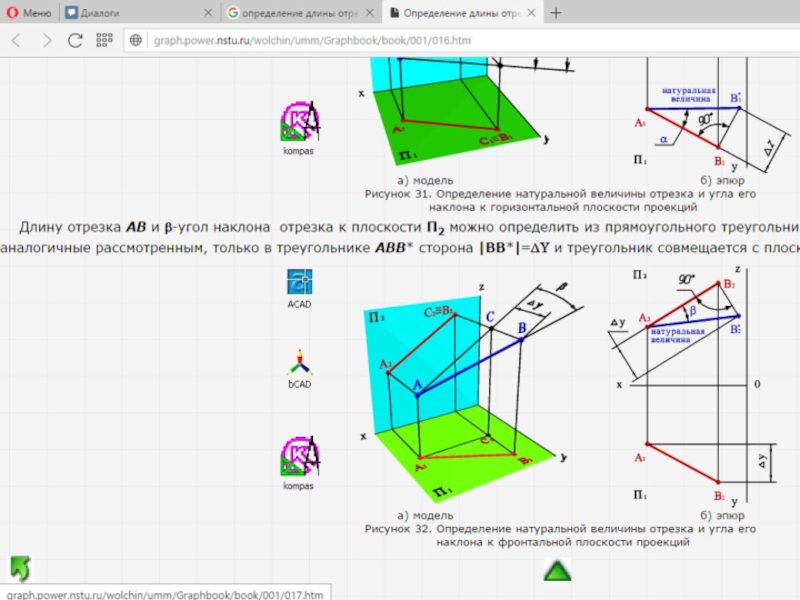
Новая проекция прямой дает истинную величину А4В4отрезка АВ (см. § 11) и позволяет определить наклон прямой к горизонтальной плоскости проекций (а = L1П1). Угол наклона прямой к фронтальной плоскости проекций (b = L1П2) можно определить, построив изображение прямой на другой дополнительной плоскости П4_|_П2 (рис. 109).
Слайд 212. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций
П4 _|_П5, причем вторая новая плоскость проекций П5 перпендикулярна самой прямой l. Так как точки А и В прямой находятся на одинаковом расстоянии от плоскости П4, то на плоскости П5получаем изображение прямой в виде точки (А5 = B5 = l5).
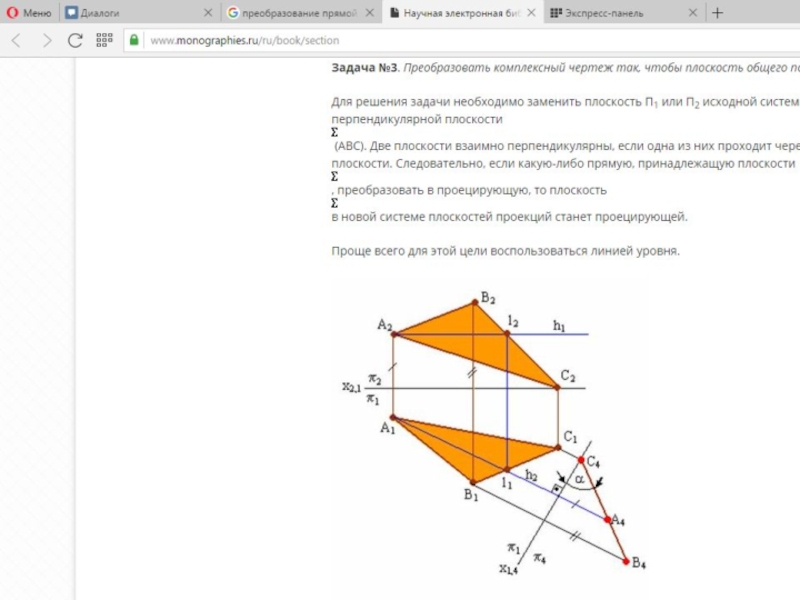
Слайд 24Преобразовать комплексный чертеж так, чтобы линия общего положения АВ стала проецирующей.
Для
Построения на комплексном чертеже:
1) провести новую ось проекций х14 // А1В1;
2) построить проекции точек А и В на плоскости П4, взяв координаты точек из плоскости П2;
3) заменить плоскость П1 на новую П5, которая будет П4 и А4В4. Для этого нужно провести новую ось проекций х4,5.
Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5, прямая АВ (А5В5) в новой системе плоскостей проекций заняла проецирующее положение и стала горизонтально проецирующей. Прямую общего положения преобразовать в проецирующую заменой только одной плоскости проекций нельзя, так как плоскость П5 перпендикулярная прямой, не будет перпендикулярна ни одной из «старых» плоскостей проекций, и, следовательно, не сможет образовать ни с одной из них прямоугольной системы плоскостей проекций.
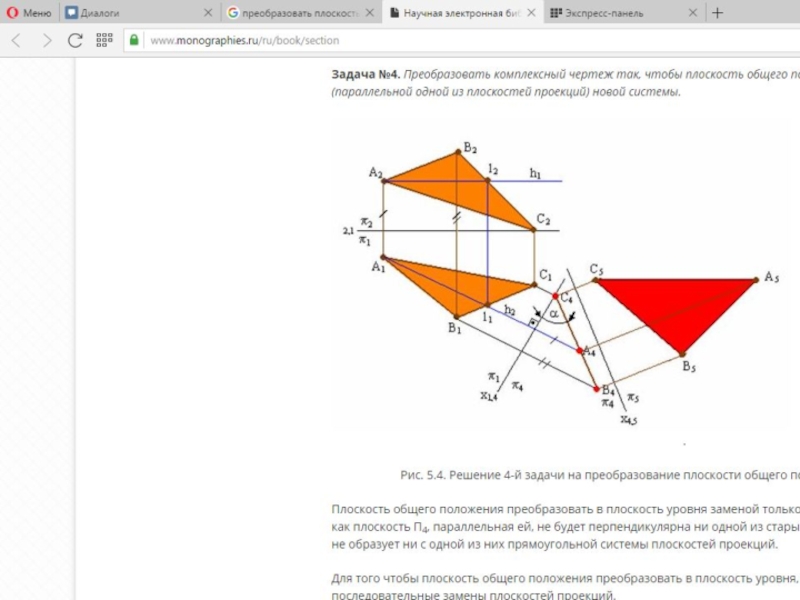
Для того чтобы прямую общего положения преобразовать в проецирующую, необходимо выполнить две последовательные замены плоскостей проекций. Прямую общего положения следует преобразовать в линию уровня, а затем линию уровня преобразовать в проецирующую (рис. 5.2).
Слайд 26
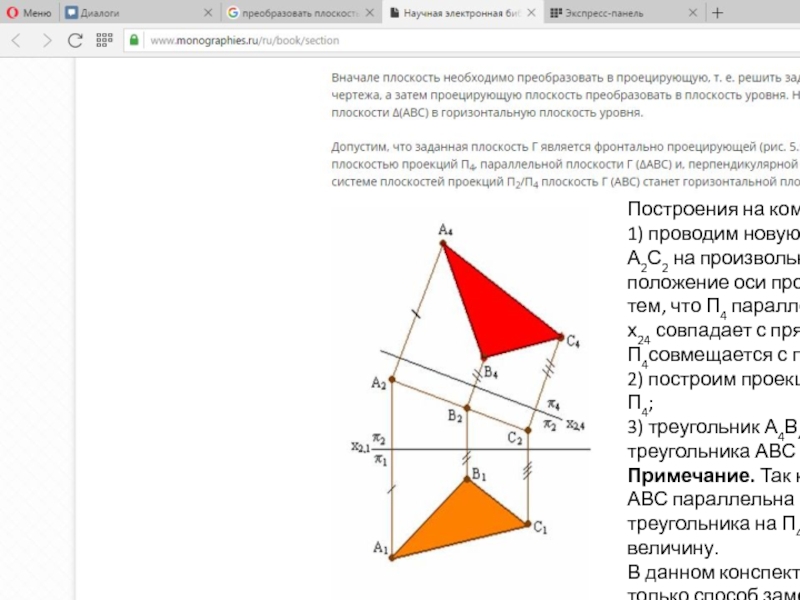
Построения на комплексном чертеже:
1) проводим новую ось проекций х24 параллельно А2С2 на произвольном
2) построим проекции точек А, В и С на плоскость П4;
3) треугольник А4В4С4 является проекцией треугольника АВС на плоскость П4.
Примечание. Так как плоскость треугольника АВС параллельна П4, значит отображение этого треугольника на П4 будет в натуральную величину.
В данном конспекте лекций рассматривается только способ замены плоскостей проекций
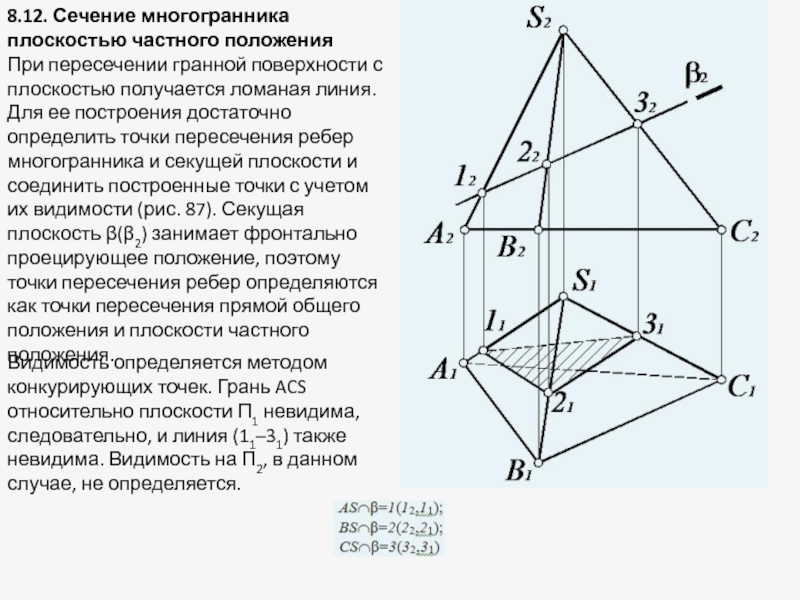
Слайд 288.12. Сечение многогранника плоскостью частного положения
При пересечении гранной поверхности с плоскостью
Видимость определяется методом конкурирующих точек. Грань ACS относительно плоскости П1 невидима, следовательно, и линия (11–31) также невидима. Видимость на П2, в данном случае, не определяется.
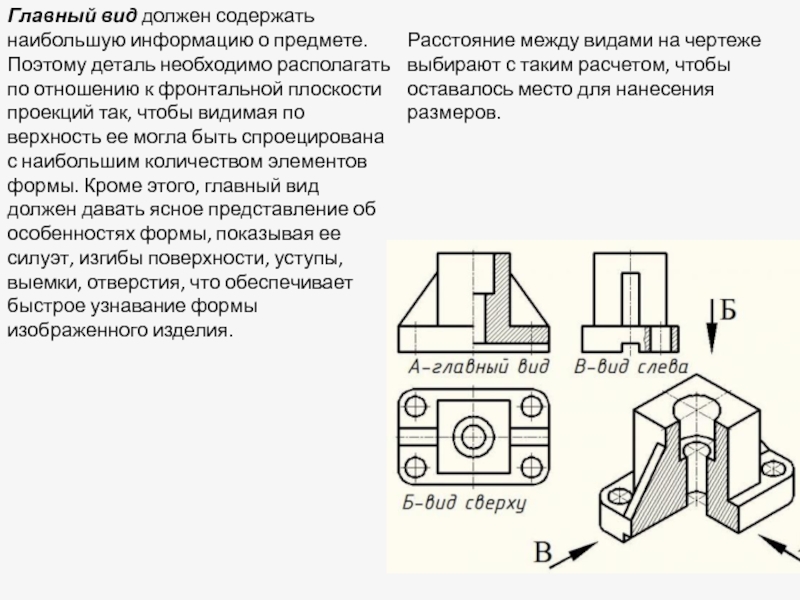
Слайд 30Главный вид должен содержать наибольшую информацию о предмете. Поэтому деталь необходимо располагать
Расстояние между видами на чертеже выбирают с таким расчетом, чтобы оставалось место для нанесения размеров.
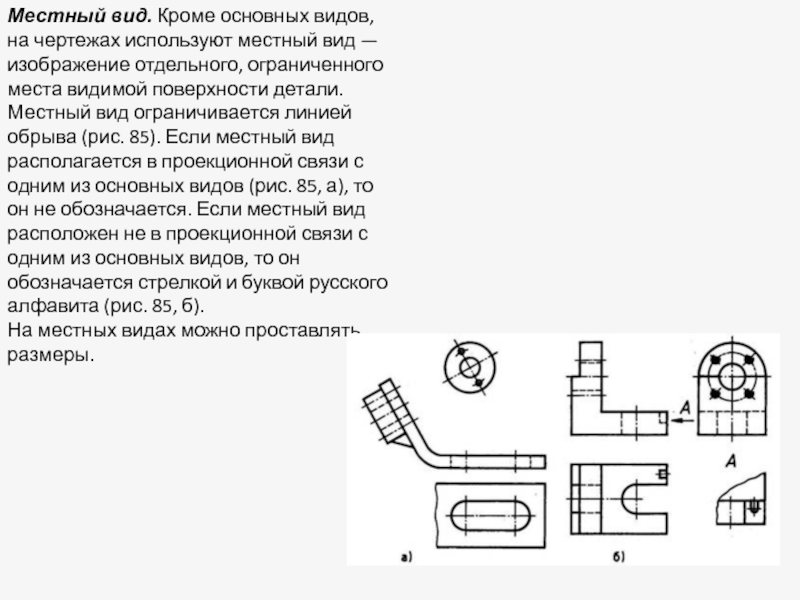
Слайд 31Местный вид. Кроме основных видов, на чертежах используют местный вид — изображение
Местный вид ограничивается линией обрыва (рис. 85). Если местный вид располагается в проекционной связи с одним из основных видов (рис. 85, а), то он не обозначается. Если местный вид расположен не в проекционной связи с одним из основных видов, то он обозначается стрелкой и буквой русского алфавита (рис. 85, б).
На местных видах можно проставлять размеры.