- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Операции с множествами. Основные понятия графов. Комбинаторика презентация
Содержание
- 1. Операции с множествами. Основные понятия графов. Комбинаторика
- 2. Основные вопросы Элементы и множества. Операции над
- 3. ЭЛЕМЕНТЫ И МНОЖЕСТВА. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ И ИХ СВОЙСТВА.
- 4. «Множество есть многое, мыслимое нами как единое»
- 5. Понятия теории множеств
- 6. С понятием множества мы соприкасаемся прежде всего
- 7. Примеры множеств: множество учащихся в данной аудитории;
- 8. Если элемент x принадлежит множеству X, то
- 9. Множество четырехугольников Пространственные тела 1, 2, 3,
- 10. Множества, элементами которых являются числа, называются числовыми множествами.
- 11. Обозначения некоторых числовых множеств:
- 12. Способы задания множеств Множество может быть
- 13. Примеры
- 14. Примеры
- 15. Виды множеств:
- 16. Если элементы множества можно сосчитать, то множество
- 17. Если элементы множества сосчитать невозможно, то множество
- 18. Множество, не содержащее ни одного элемента, называется
- 19. Мощность множества Число элементов конечного множества называют
- 20. Пример . Определите мощность какого из множеств
- 21. Отношения между множествами Наглядно отношения между
- 22. При графическом изображении множеств удобно использовать диаграммы
- 23. Множество A называется подмножеством множества B, если
- 24. Свойства множеств Любое множество является подмножеством самого
- 25. Два множества А и В называются равными
- 26. Количество подмножеств Если мощность множества n, то
- 27. В={1,3,5} Подмножества В: {∅}, {1}, {3}, {5},
- 28. Операции над множествами Пересечением (произведением) множеств А
- 29. Например, если А={a,b,c}, B={b,c,f,e}, то А ∩ В = {b} Операции над множествами пересечение
- 30. Операции над множествами
- 31. Объединением (суммой) двух множеств А и В
- 32. объединение Например, если А={1,2,4}, B={3,4,5,6},
- 33. Операции над множествами
- 34. Разностью множеств А и В называется множество
- 35. разность Например, если А={1,2,3,4}, B={3,4,5}, то
- 36. Операции над множествами
- 37. Операции над множествами Дополнение множества Часто множества
- 38. Если А - множество параллелограммов, В- множество
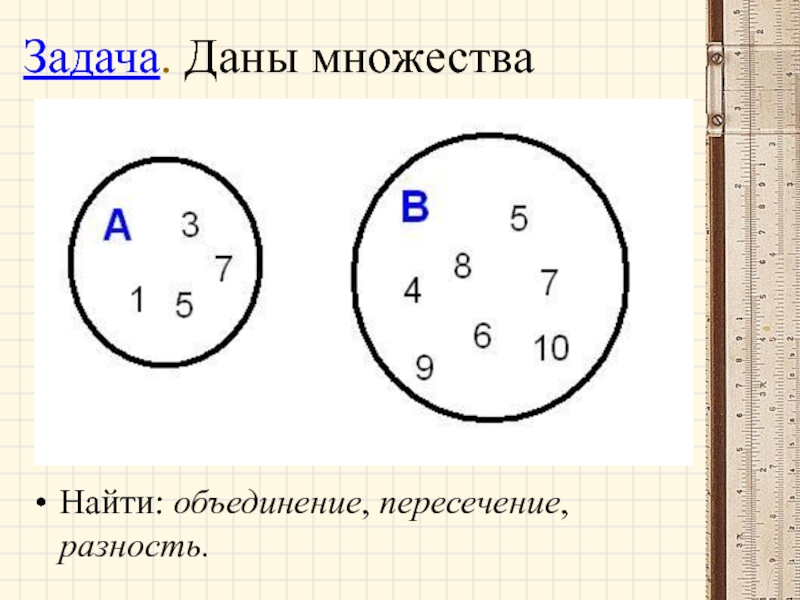
- 39. Задача. Даны множества Найти: объединение, пересечение, разность.
- 44. Всего 67 Английский 47
- 45. Задача. Каждый учащийся в классе изучает английский
- 46. Задача. Каждая семья, живущая в нашем доме,
- 47. ГРАФЫ. ЭЛЕМЕНТЫ ГРАФОВ. ВИДЫ ГРАФОВ И ОПЕРАЦИИ НАД НИМИ
- 48. Теория графов представляет собой раздел математики, имеющий
- 49. История возникновения графов Термин "граф" впервые появился
- 50. В основе теории лежит понятие графа. Граф
- 51. СОСТАВ ГРАФА Граф состоит из вершин, связанных
- 52. Ориентированный граф - граф, вершины которого
- 53. Взвешенный граф Это граф, рёбрам или дугам
- 54. Две вершины графа называются смежными, если существует
- 55. Если граф G имеет ребро , у
- 56. Два ребра называются смежными, если они имеют
- 57. Рёбра, которые начинаются в одной и той
- 58. На рисунке кратными являются, например, рёбра х1(А,
- 59. На рисунке вершина А имеет степень, равную
- 60. E Вершина графа, имеющая степень, равную нулю,
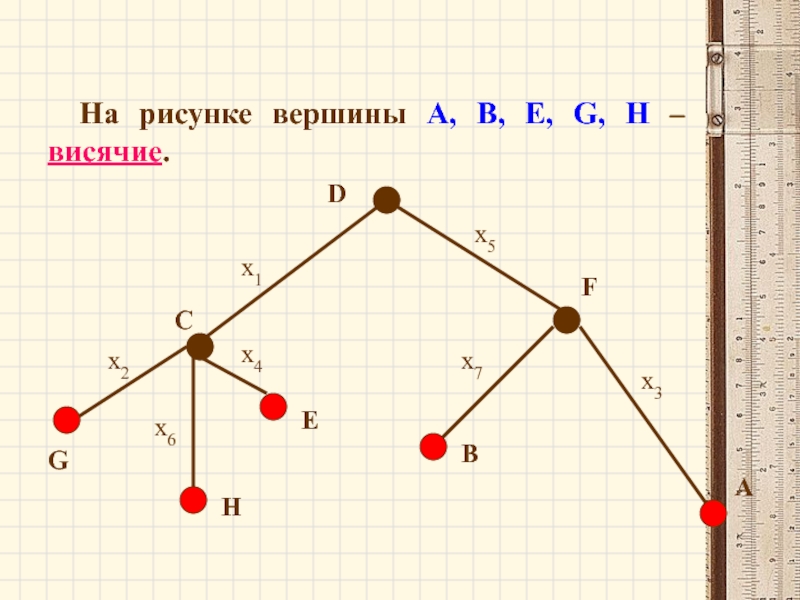
- 61. На рисунке вершины А, В, Е,
- 62. Теорема 1. В графе
- 63. Вершина называется чётной (нечётной), если её степень
- 64. Теорема 2. Число нечётных вершин любого графа
- 65. Дополнением графа называется граф
- 66. ПУТИ И МАРШРУТЫ В ГРАФАХ Путем
- 67. В качестве примера рассмотрим орграф, представленный на
- 68. Неориентированный граф называется связным, если существует хотя
- 69. Путь называется замкнутым, если начальная и конечная
- 70. Последовательность попарно смежных вершин неориентированного графа, т.е.
- 71. На рисунке HCDFD – маршрут длиной 4.
- 72. В графе на рисунке (t, s, p,
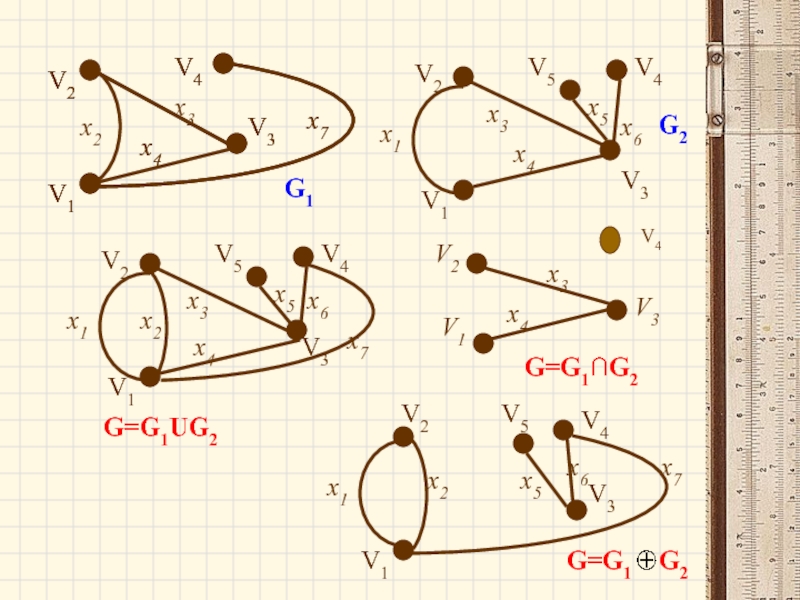
- 73. ОПЕРАЦИИ НАД ГРАФАМИ Объединением графов
- 74. х3 х4 х6 G1
- 75. ОБОСНОВАНИЕ ОСНОВНЫХ ПОНЯТИЙ КОМБИНАТОРИКИ: ФАКТОРИАЛ, ПЕРЕСТАНОВКИ, РАЗМЕЩЕНИЯ, СОЧЕТАНИЯ.
- 76. Комбинаторикой называется раздел математики, в котором исследуется,
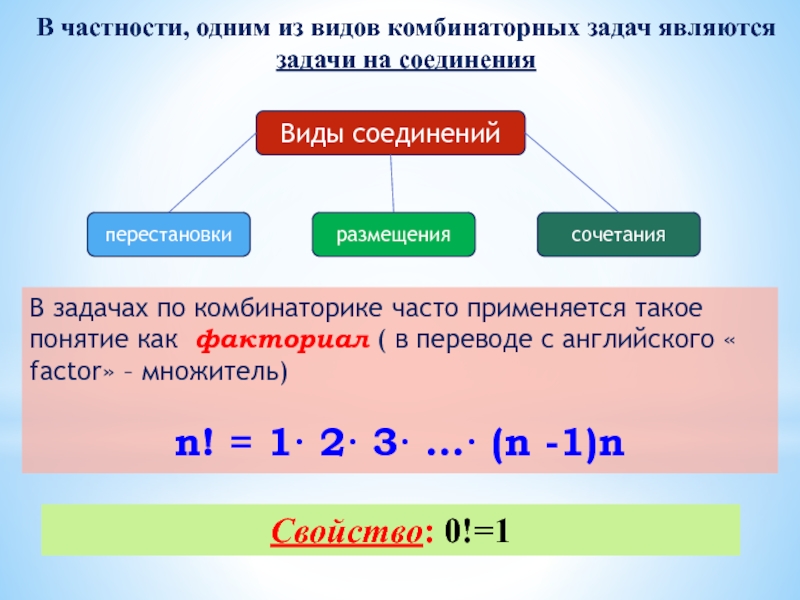
- 77. В частности, одним из видов комбинаторных задач
- 78. Перестановки Множество называется упорядоченным, если
- 79. Пример 1: В расписании сессии 3 экзамена
- 80. Пример 2 Перестановки множества А={a, b, c}
- 81. Перестановки с повторениями Рассматривая перестановки ранее,
- 82. Пример 5. Слова и фразы с переставленными
- 83. Размещения Размещением из n элементов по
- 84. Решение: Требуется выделить упорядоченные трехэлементные подмножества
- 85. Решение (обратить внимание на его оформление!) Основное
- 86. Размещения с повторениями Размещения с повторениями –
- 87. Пример 9. В библиотеку, в которой есть
- 88. Сочетания Сочетанием из n элементов
- 89. Решение. (обратить внимание на его оформление!) Основное
- 90. Сочетания с повторениями Сочетаниями с повторениями из
- 91. Сочетания с повторениями Если из множества,
- 92. Пример 11. Сколько костей находится в обычной
- 93. Спасибо за внимание!
Слайд 2Основные вопросы
Элементы и множества. Операции над множествами и их свойства.
Графы.
Обоснование основных понятий комбинаторики: факториал, перестановки, размещения, сочетания.
Слайд 4«Множество есть многое, мыслимое нами как единое»
основатель теории множеств – Георг
(1845—1918) — немецкий математик, логик, теолог, создатель теории бесконечных множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв.
Слайд 5Понятия теории множеств
Понятие множества является одним из наиболее
Множество - совокупность объектов, обладающих определенным свойством, объединенных в единое целое.
Слайд 6С понятием множества мы соприкасаемся прежде всего тогда, когда по какой-либо
Множества принято обозначать заглавными латинскими буквами: А, В, С, D .
Объекты, которые образуют множество, называют элементами множества и для обозначения элементов используют, как правило, малые буквы латинского алфавита.
Слайд 7Примеры множеств:
множество учащихся в данной аудитории;
множество людей, живущих на нашей планете
множество точек данной геометрической фигуры; множество чётных чисел;
множество корней уравнения х2-5х+6=0;
множество действительных корней уравнения х2+9=0;
Слайд 8Если элемент x принадлежит множеству X, то записывают x ∈ Х
В противном случае, если a не принадлежит множеству А, будем использовать обозначение ∉:
Если множество А является частью множества В, то записывают А ⊂В (⊂ — содержится).
Слайд 9Множество четырехугольников
Пространственные тела
1, 2, 3, 4, 5, 6, 7, 8, 9,
Квадраты чисел
Цифры десятичной системы счисления
10, 12, 14, 16 … 96, 98
Слайд 11 Обозначения некоторых числовых множеств:
N – множество натуральных
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел.
Слайд 12Способы задания множеств
Множество может быть задано перечислением всех его элементов
2. Множество может быть задано описанием свойств его элементов. Чаще всего при этом используют запись, которую читают следующим образом: «A есть множество элементов b таких, что для них выполняется свойство B». Например, а – четное натуральное число.
3. Множество может быть задано указанием характеристического свойства его элементов , то есть такого свойства, которым обладают все элементы данного множества, и только они:
Здесь x ∈ М означает, что элемент х является элементом известного множества .
Запись Р(х) означает, что элемент х обладает свойством Р. Свойство Р(х) формулируется словами, символами или выражается с помощью уравнения или неравенства.
Слайд 16Если элементы множества можно сосчитать, то множество является КОНЕЧНЫМ
Пример
Множество гласных
Слайд 17Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕ
Пример
Множество натуральных чисел бесконечно.
Пример
Множество
Пример
Множество атомов во Вселенной
Слайд 18Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается
Пример
Множество действительных корней уравнения x2 +1=0.
Пример
Множество людей, проживающих на Солнце.
Слайд 19Мощность множества
Число элементов конечного множества называют мощностью этого множества и обозначают
Количество элементов в конечном множестве естественно характеризовать их числом.
В этом смысле множество чисел {-2, 0, 3,8} и множество букв {с, х, ф, а} эквивалентны, так как они содержат одинаковое число элементов.
Слайд 20Пример . Определите мощность какого из множеств A = {1, 3,
Решение. Понятие мощности конечных множеств позволяет сравнивать их по количеству элементов.
Так, если A = {1, 3, 5, 7, 9}, а
B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4 и потому m (A) > m (B).
Слайд 21Отношения между множествами
Наглядно отношения между множествами изображают при помощи особых
Для этого множества, сколько бы они ни содержали элементов, представляют в виде кругов или любых других замкнутых кривых (фигур)
Слайд 22При графическом изображении множеств удобно использовать диаграммы Венна, на которых универсальное
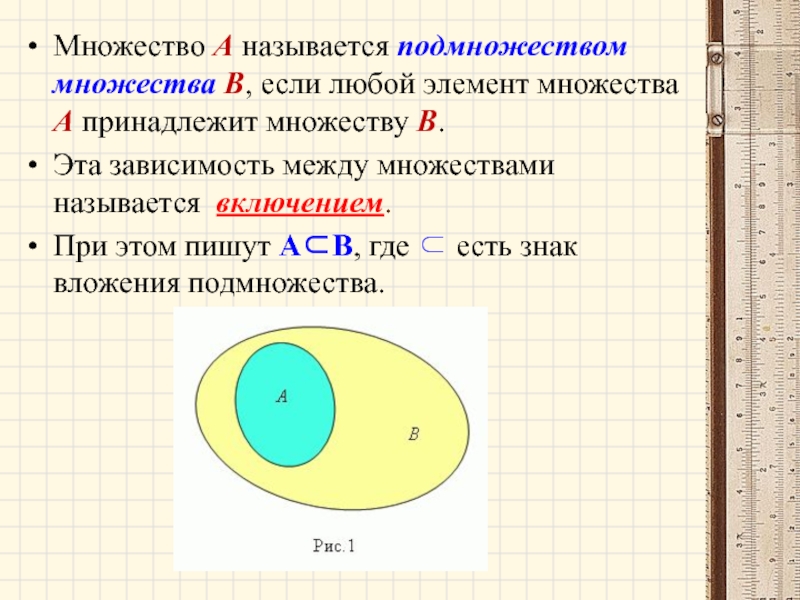
Слайд 23Множество A называется подмножеством множества B, если любой элемент множества A
Эта зависимость между множествами называется включением.
При этом пишут A⊂B, где ⊂ есть знак вложения подмножества.
Слайд 24Свойства множеств
Любое множество является подмножеством самого себя (рефлексивность): A⊂ B.
Для любых
и , то .
Для всякого множества А пустое множество ∅ является его подмножеством: ∅⊂ А
Слайд 25 Два множества А и В называются равными ( А = В
Примеры
1. , . Множества и состоят из одних и тех же элементов, поэтому они равные: А = В .
2. Множество решений уравнения есть множество чисел 2 и 3, то есть . Множество В простых чисел, меньших 5, также состоит из чисел 2 и 3, то есть .
Слайд 26Количество подмножеств
Если мощность множества n, то у этого множества 2n подмножеств.
А={1,2}
Подмножества
{∅}, {1}, {2}, {1,2}.
Слайд 27В={1,3,5}
Подмножества В:
{∅}, {1}, {3}, {5}, {1,3}, {1,5}, {5,3}, {1,3,5}
С={а,и,е,о}
Подмножества С:
{∅}, {а},
Количество подмножеств
Слайд 28Операции над множествами
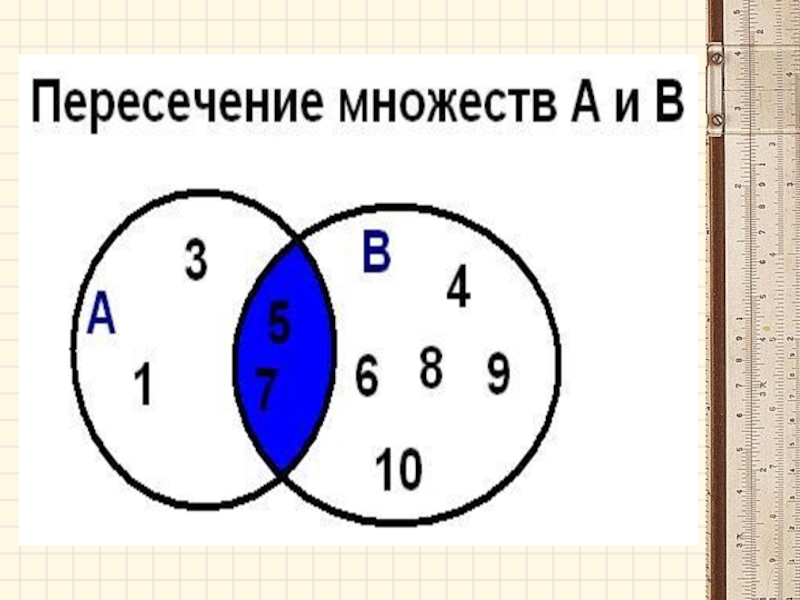
Пересечением (произведением) множеств А и В называется множество А
А∩В={х│хєА и хєВ}
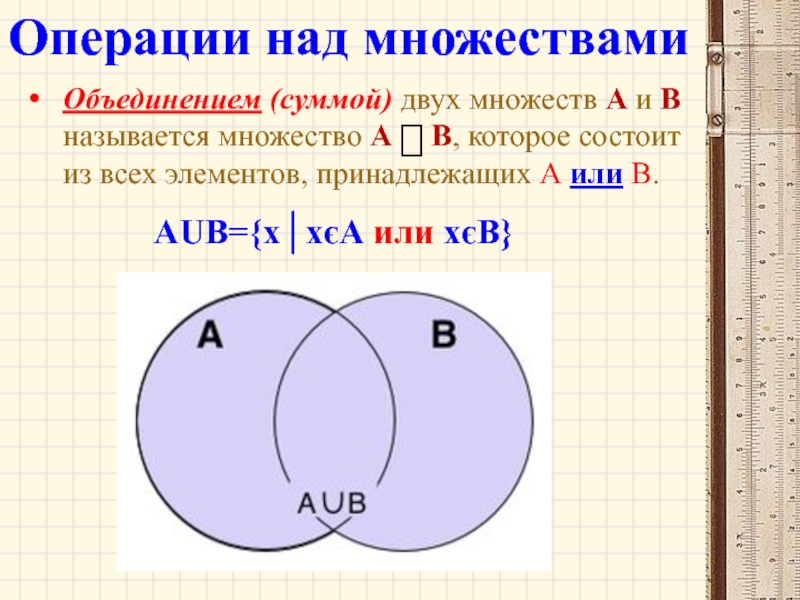
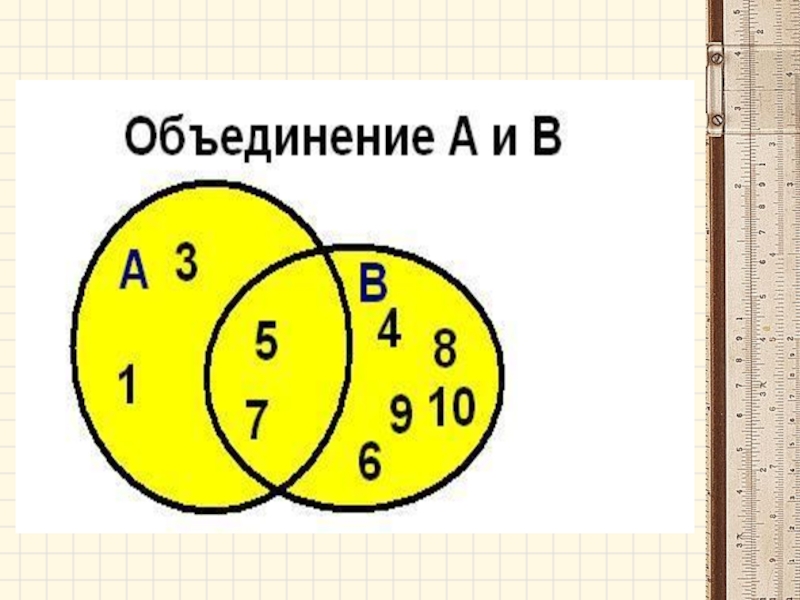
Слайд 31Объединением (суммой) двух множеств А и В называется множество А
Операции над множествами
АUВ={х│хєА или хєВ}
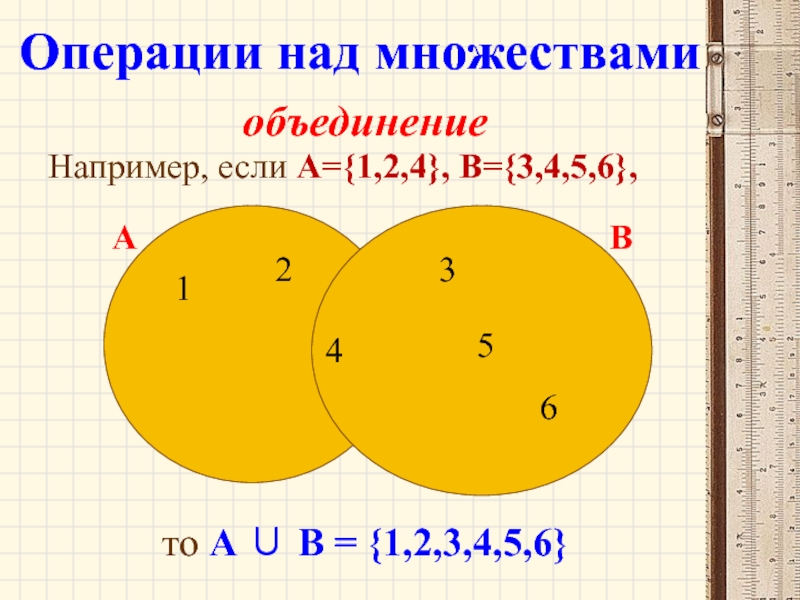
Слайд 32 объединение
Например, если А={1,2,4}, B={3,4,5,6},
то А ∪ B = {1,2,3,4,5,6}
1
2
4
А
4
3
5
6
В
Операции
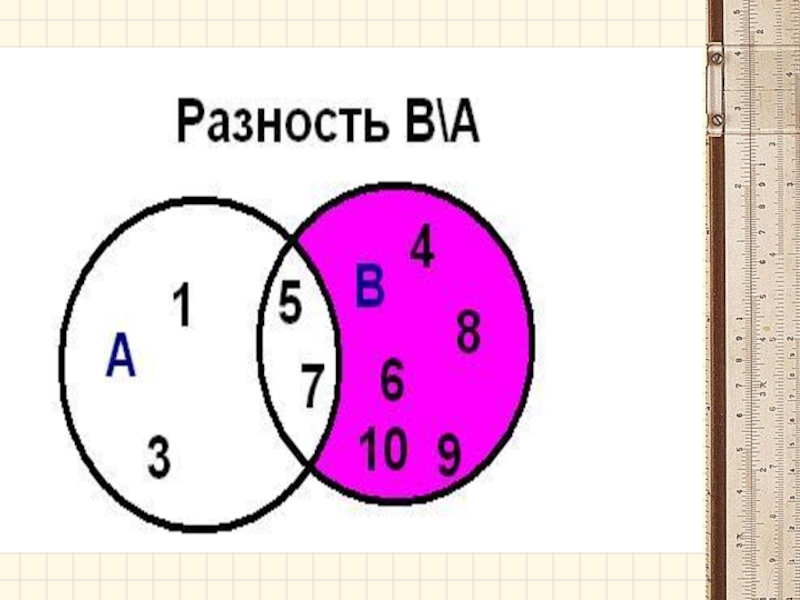
Слайд 34Разностью множеств А и В называется множество А- В, элементы которого
Операции над множествами
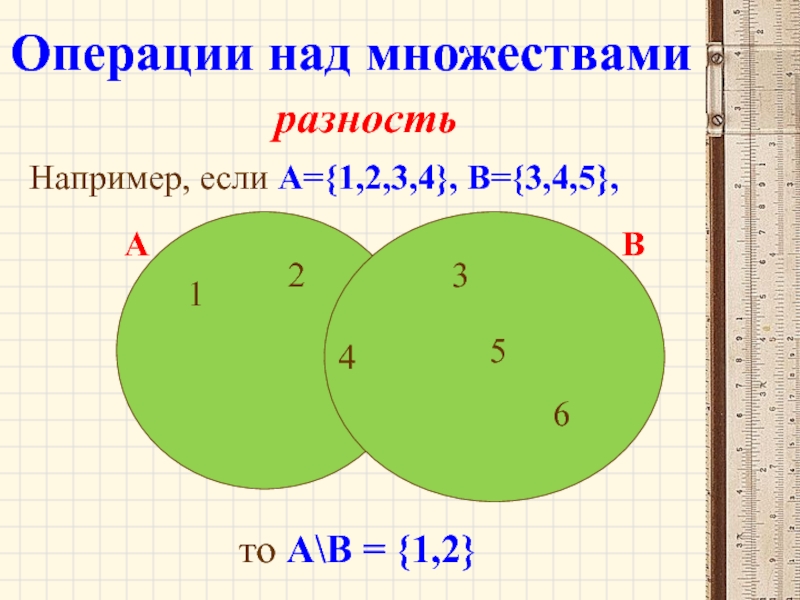
Слайд 35разность
Например, если А={1,2,3,4}, B={3,4,5},
то А\В = {1,2}
1
2
4
А
4
3
5
6
В
Операции над множествами
Слайд 37Операции над множествами
Дополнение множества
Часто множества A,B,C … являются подмножествами некоторого более
Слайд 38Если А - множество параллелограммов, В- множество трапеций, С - множество
Если А - множество треугольников, В- множество четырехугольников и так далее, то в качестве универсального множества U можно выбрать множество всех многоугольников.
Операции над множествами
ПРИМЕРЫ:
Слайд 44
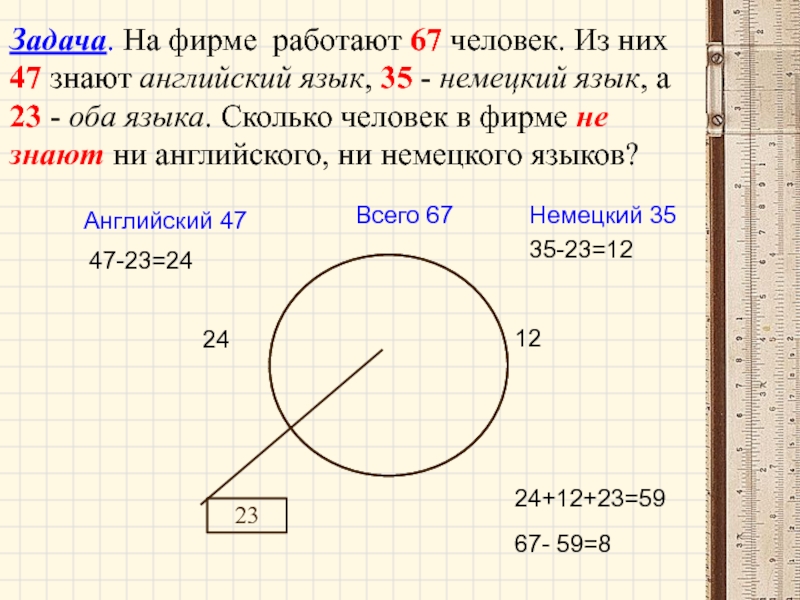
Всего 67
Английский 47
Немецкий 35
23
47-23=24
24
35-23=12
12
24+12+23=59
67- 59=8
Задача. На фирме работают 67 человек. Из
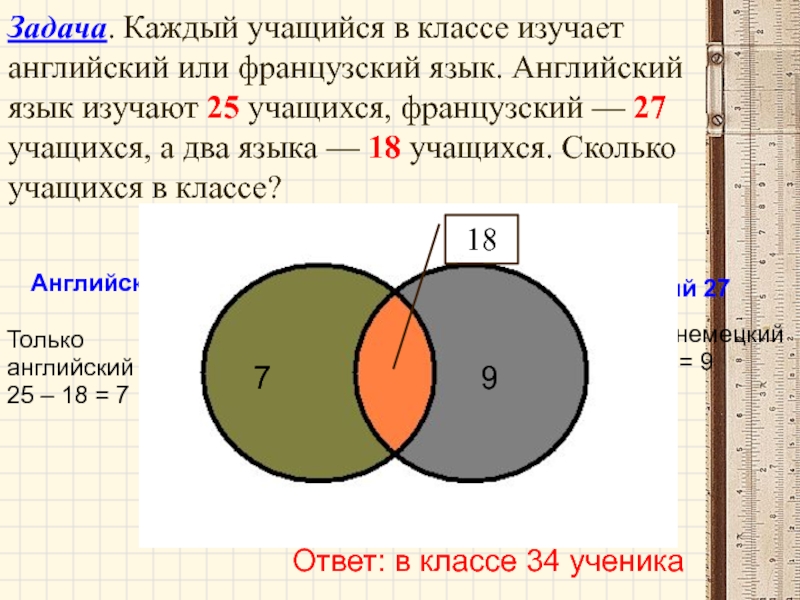
Слайд 45Задача. Каждый учащийся в классе изучает английский или французский язык. Английский
Ответ: в классе 34 ученика
Английский 25
Немецкий 27
Только английский
25 – 18 = 7
Только немецкий
27 – 18 = 9
7 + 9 + 18 = 34
18
7
9
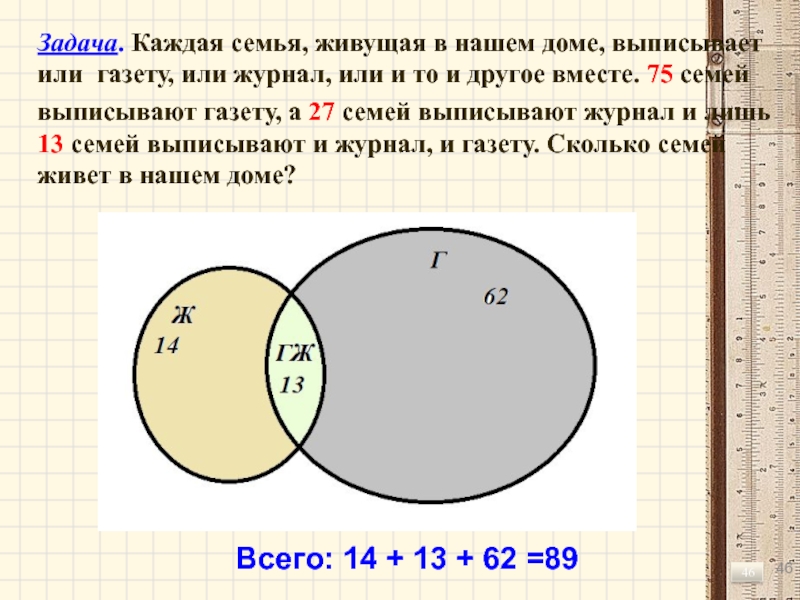
Слайд 46Задача. Каждая семья, живущая в нашем доме, выписывает или газету, или
выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?
Всего: 14 + 13 + 62 =89
Слайд 48Теория графов представляет собой раздел математики, имеющий широкие практические приложения.
Теория
Слайд 49История возникновения графов
Термин "граф" впервые появился в книге венгерского математика Д.
Слайд 50В основе теории лежит понятие графа.
Граф - совокупность конечного числа точек,
Графом называется пара двух конечных множеств: множество точек V и множество линий X (ребер, дуг), соединяющих некоторые пары точек.
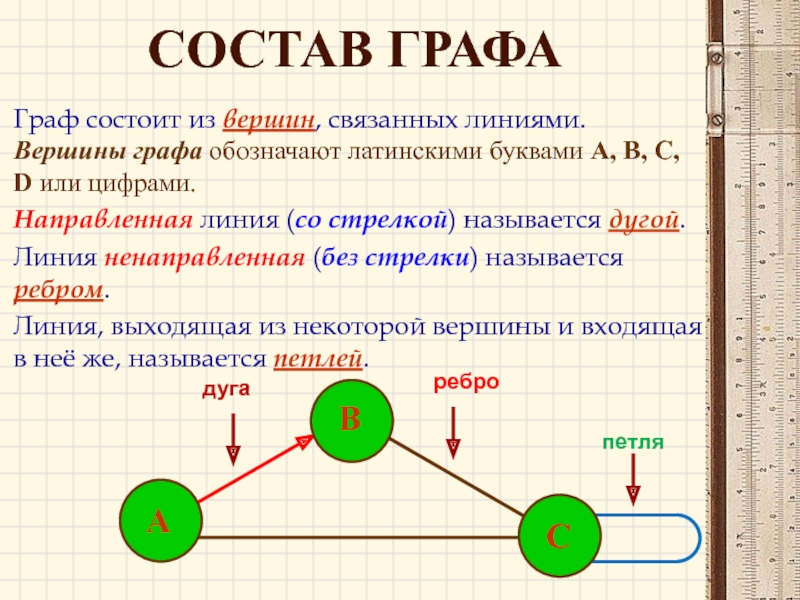
Слайд 51СОСТАВ ГРАФА
Граф состоит из вершин, связанных линиями. Вершины графа обозначают латинскими
Направленная линия (со стрелкой) называется дугой.
Линия ненаправленная (без стрелки) называется ребром.
Линия, выходящая из некоторой вершины и входящая в неё же, называется петлей.
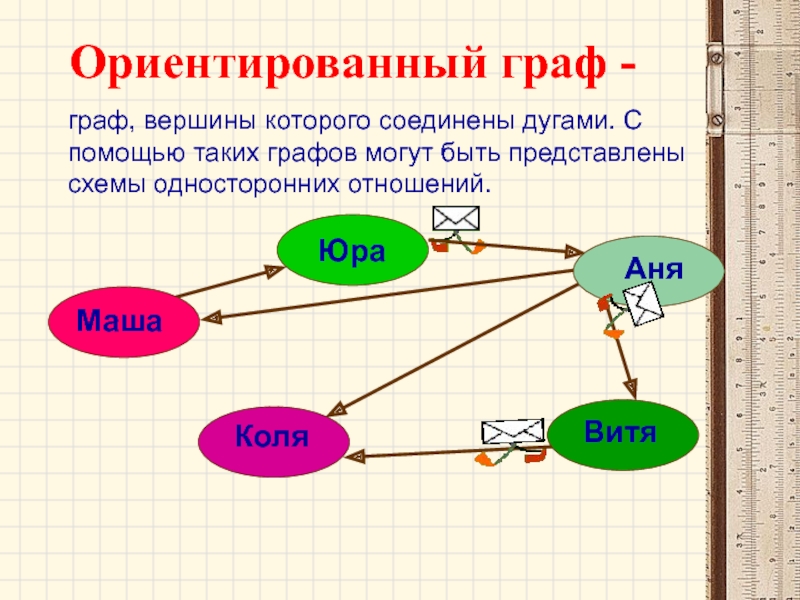
Слайд 52Ориентированный граф -
граф, вершины которого соединены дугами. С помощью таких
Маша
Юра
Аня
Витя
Коля
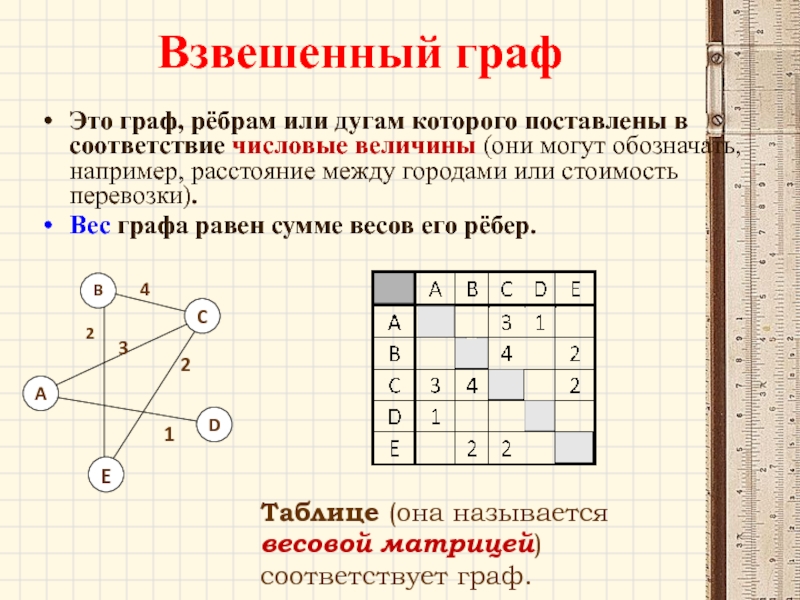
Слайд 53Взвешенный граф
Это граф, рёбрам или дугам которого поставлены в соответствие числовые
Вес графа равен сумме весов его рёбер.
Таблице (она называется весовой матрицей) соответствует граф.
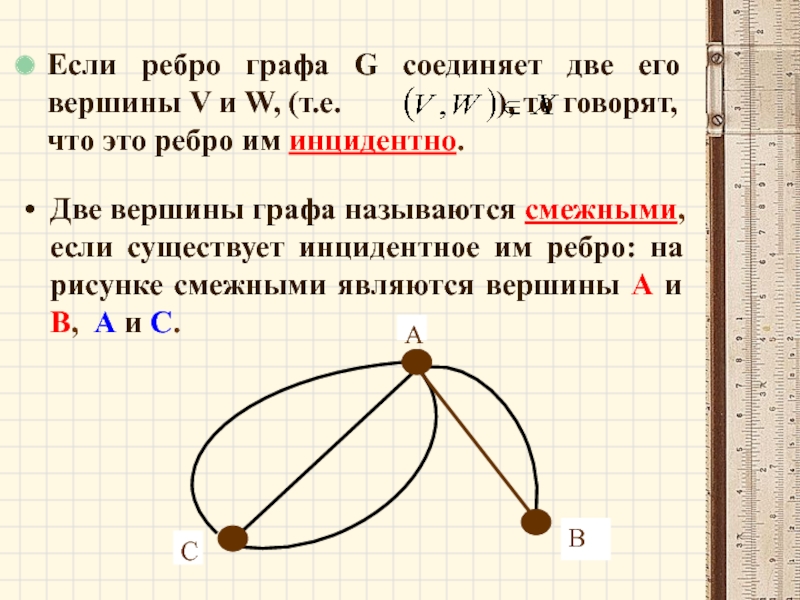
Слайд 54Две вершины графа называются смежными, если существует инцидентное им ребро: на
Если ребро графа G соединяет две его вершины V и W, (т.е. ), то говорят, что это ребро им инцидентно.
Слайд 55Если граф G имеет ребро , у которого начало и конец
С
A
B
D
E
q
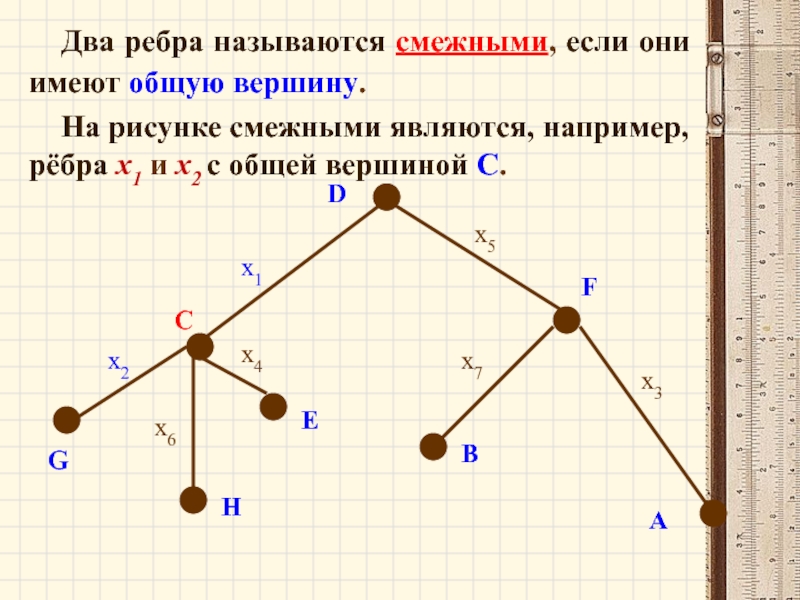
Слайд 56Два ребра называются смежными, если они имеют общую вершину.
На рисунке
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G
Слайд 57Рёбра, которые начинаются в одной и той же вершине, заканчиваются также
Количество одинаковых пар вида называется кратностью ребра
Число рёбер, инцидентных вершине А, называется степенью этой вершины и обозначается (от англ. degree – степень).
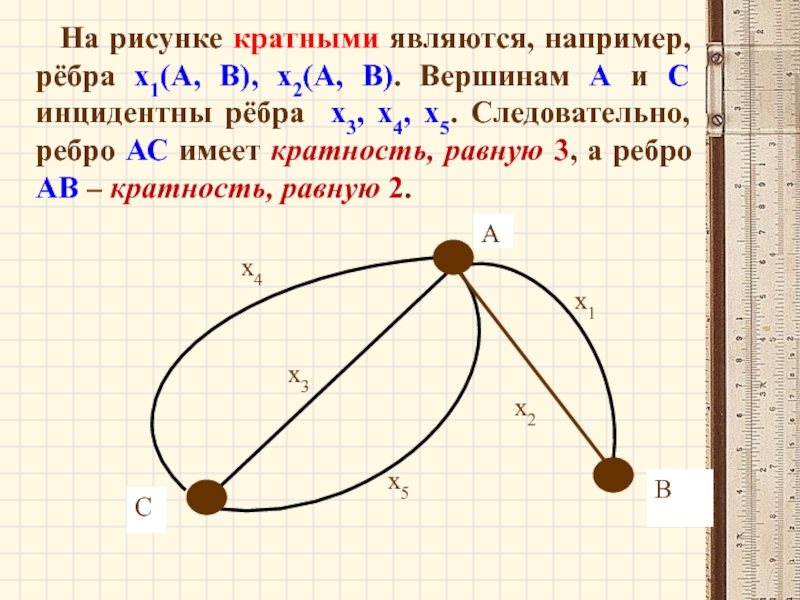
Слайд 58На рисунке кратными являются, например, рёбра х1(А, В), х2(А, В). Вершинам
А
С
В
х1
х2
х5
х3
х4
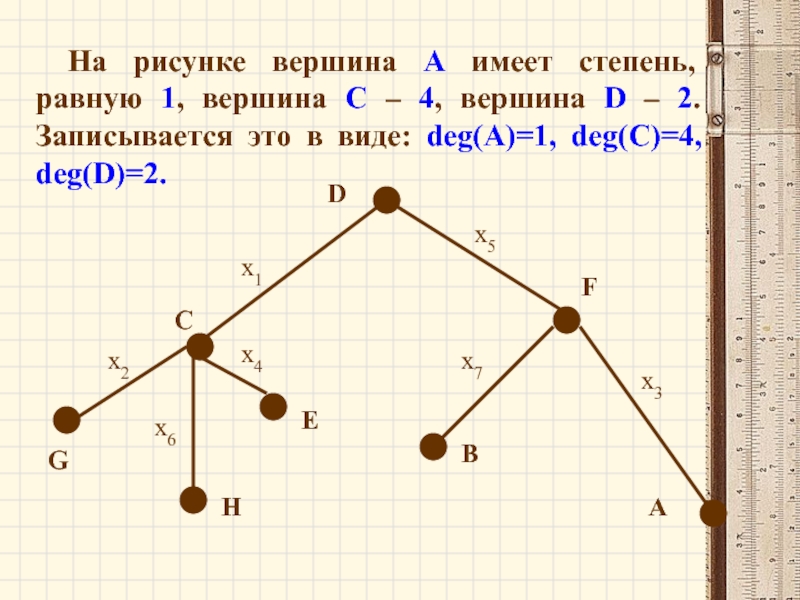
Слайд 59На рисунке вершина А имеет степень, равную 1, вершина С –
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G
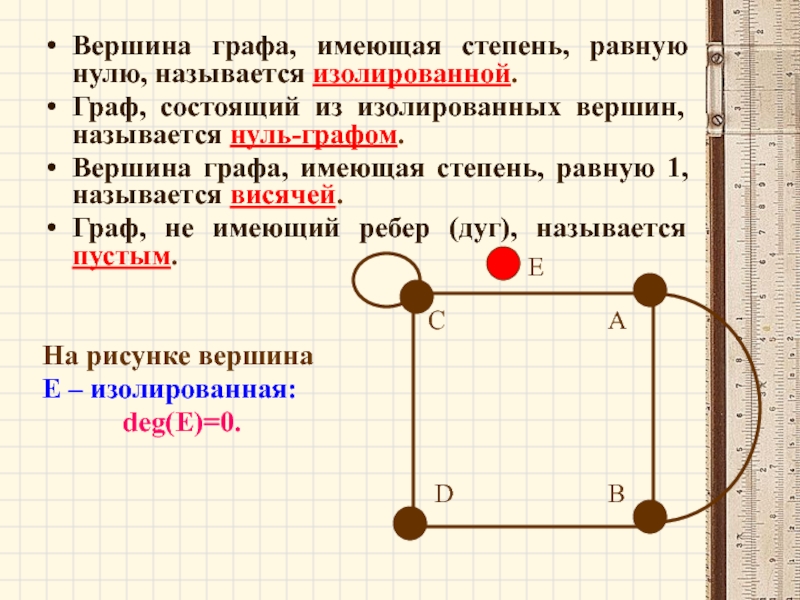
Слайд 60E
Вершина графа, имеющая степень, равную нулю, называется изолированной.
Граф, состоящий из
Вершина графа, имеющая степень, равную 1, называется висячей.
Граф, не имеющий ребер (дуг), называется пустым.
На рисунке вершина
Е – изолированная:
deg(E)=0.
A
B
D
C
Слайд 62
Теорема 1. В графе сумма степеней всех его
где - число вершин;
- число рёбер графа.
Слайд 63Вершина называется чётной (нечётной), если её степень – чётное (нечётное) число.
На рисунке deg(D)=2, deg(F)=3, значит у графа вершина D является чётной, а F – нечётной.
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G
Слайд 64 Теорема 2. Число нечётных вершин любого графа – чётно.
Следствие. Невозможно начертить
Граф G называется полным,
если любые две его различные
вершины соединены одним и
только одним ребром.
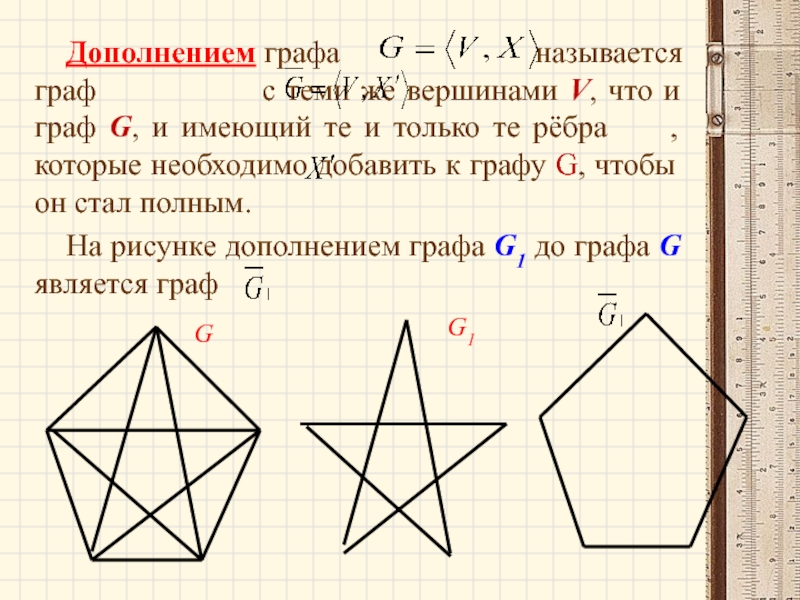
Слайд 65Дополнением графа называется граф
На рисунке дополнением графа G1 до графа G является граф
G
G1
Слайд 66ПУТИ И МАРШРУТЫ В ГРАФАХ
Путем в ориентированном графе называется последовательность дуг,
Вершина, от которой проложен маршрут, называется началом пути, вершина в конце маршрута — конец пути.
Путь, в котором каждая вершина используется не более одного раза, называется простым путем.
Длиной пути в графе называется количество дуг (ребер), составляющих этот путь.
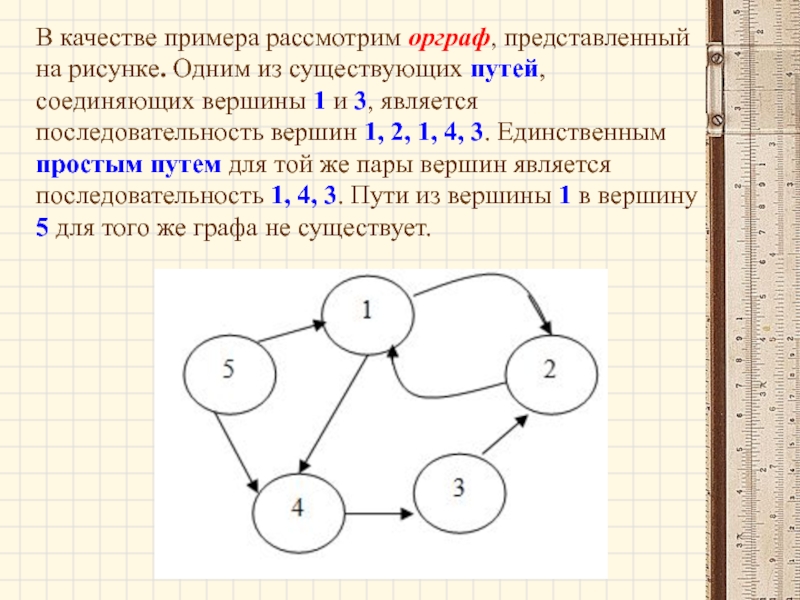
Слайд 67В качестве примера рассмотрим орграф, представленный на рисунке. Одним из существующих
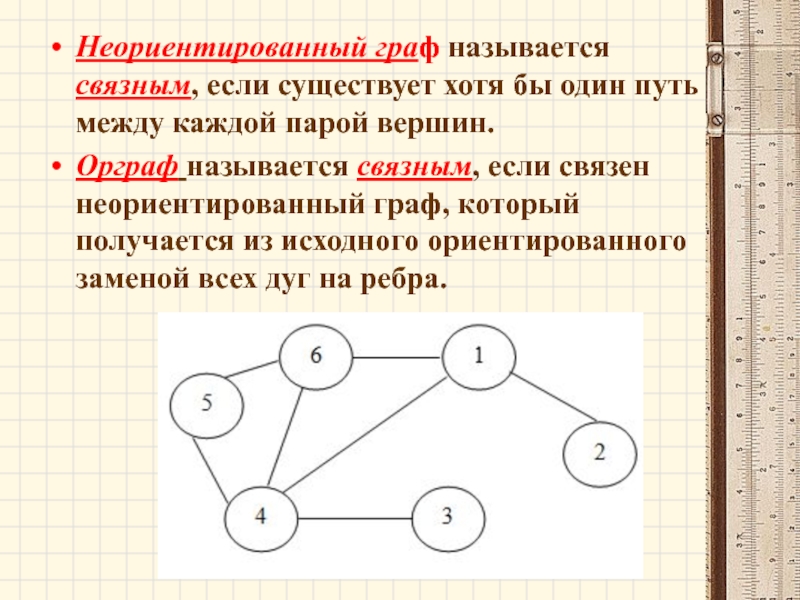
Слайд 68Неориентированный граф называется связным, если существует хотя бы один путь между
Орграф называется связным, если связен неориентированный граф, который получается из исходного ориентированного заменой всех дуг на ребра.
Слайд 69Путь называется замкнутым, если начальная и конечная вершины совпадают.
Замкнутый путь называется
Рассмотрим граф. Для него путь 2, 1, 6, 5, 4, 1, 2 является замкнутым; а путь 1, 6, 5, 4, 1 является циклом.
Слайд 70Последовательность попарно смежных вершин неориентированного графа, т.е. последовательность рёбер неориентированного графа,
Число рёбер маршрута называется длиной маршрута.
Если начальная вершина маршрута совпадает с конечной, то такой маршрут называется замкнутым или циклом.
Слайд 71На рисунке HCDFD – маршрут длиной 4. Обозначение: |HCDFD|=4. Маршрут принято
х1
х2
х3
х4
х5
х6
х7
С
D
F
A
B
E
H
G
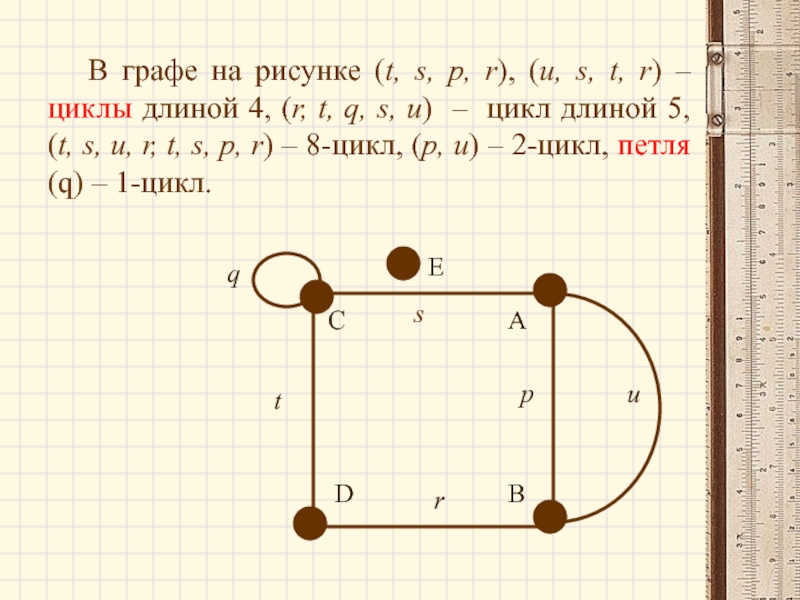
Слайд 72 В графе на рисунке (t, s, p, r), (u, s, t,
s
Слайд 73ОПЕРАЦИИ НАД ГРАФАМИ
Объединением графов
Пересечением графов и называется граф , для которого - множество рёбер, а - множество вершин.
Кольцевой суммой двух графов называется граф ,порождённый множеством вершин и множеством рёбер , т.е. множеством рёбер, содержащихся либо в , либо в , но не в .
Слайд 76Комбинаторикой называется раздел математики, в котором исследуется, сколько различных комбинаций (всевозможных
Слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать».
Слайд 77В частности, одним из видов комбинаторных задач являются
задачи на соединения
Виды
размещения
сочетания
перестановки
В задачах по комбинаторике часто применяется такое понятие как факториал ( в переводе с английского « factor» – множитель)
n! = 1· 2· 3· …· (n -1)n
Свойство: 0!=1
Слайд 78
Перестановки
Множество называется упорядоченным, если каждому элементу этого множества поставлено в
Перестановки – различные упорядоченные множества, которые отличаются лишь порядком элементов.
Термин “перестановка” употребил впервые Якоб Бернулли в книге «Искусство предположений».
Р – первая буква французского слова permutation – перестановка.
Формула (число размещений «из эн по эм»):
(1654-1705)
Слайд 79Пример 1: В расписании сессии 3 экзамена (история, геометрия, алгебра). Сколько
Решение. (обратить внимание на его оформление!)
Основное множество: {история, геометрия, алгебра} ⇒
Соединение – вариант расписания сессии
Проверим, важен ли порядок:
{история, геометрия, алгебра} и {геометрия, история, алгебра} – варианты расписания сессии для разных групп ⇒ порядок важен ⇒ это последовательность ⇒ это перестановка из трех элементов.
Перестановки
Ответ: 6 вариантов
Слайд 80Пример 2
Перестановки множества А={a, b, c} из трёх элементов имеют вид:
(a,
(a, c, b); (b, a, c); (c, b, a),
т. е. P3 = 3! = 1х2х3 = 6 перестановок.
Пример 3
Сколькими способами можно разместить на полке 4 книги?
P4 = 4! = 1х2х3х4 = 24 способа.
Перестановки
Слайд 81 Перестановки с повторениями
Рассматривая перестановки ранее, мы предполагали, что n элементов
Если среди n элементов есть n1 элемент одного вида, n2 элементов другого вида и т.д., nk элементов k-го вида, то имеем перестановки с повторениями, их число:
Пример 4.
Сколько различных «слов» можно составить из букв слова ДЕД?
n=3, k=2, n1=2, n2=1
Слайд 82 Пример 5. Слова и фразы с переставленными буквами называют анаграммами. Сколько
Решение.
Всего в слове «МАКАКА» 6 букв (m=6).
Определим сколько раз в слове используется каждая буква:
«М» - 1 раз (k1=1)
«А» - 3 раза (k2=3)
«К» - 2 раза (k3=2)
Р =
m!
k1! k2! …kn!
Р1,3,2 =
6!
1! 3! 2!
=
4*5*6
2
=
60.
Перестановки с повторениями
Слайд 83 Размещения
Размещением из n элементов по m ( m ≤ n)
Формула (число размещений «из эн по эм»):
Пример 6.
Сколькими способами можно рассадить 4 учащихся на 25 мест?
Два размещения из n элементов считаются различными, если они отличаются самими элементами или порядком их расположения.
Слайд 84 Решение:
Требуется выделить упорядоченные трехэлементные подмножества множества, содержащего 40 элементов, т.е.
Размещения
Пример 7. Сколькими способами из 40 учеников класса можно выделить актив в следующем составе: староста, физорг и редактор стенгазеты?
Слайд 85Решение (обратить внимание на его оформление!)
Основное множество: {1, 3, 5, 7,
Соединение – двузначное число ⇒
Пример 8. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различны и нечетны?
Проверим, важен ли порядок:
разные двузначные числа ⇒
порядок важен ⇒ это последовательность ⇒ это размещение «из пяти по два».
двузначных чисел
Ответ: 20 чисел.
Размещения
Слайд 86Размещения с повторениями
Размещения с повторениями – соединения, содержащие n элементов, выбираемых
Их количество в предположении неограниченности количества элементов каждого вида равно
Слайд 87Пример 9. В библиотеку, в которой есть много одинаковых учебников по
Размещения с повторениями
Решение: Так как учебники по каждому предмету одинаковые, и библиотекарь записывает лишь название (без номера),то список – размещение с повторением, число элементов исходного множества равно 10, а количество позиций – 5.
Тогда количество разных списков равно
= 100000.
Ответ: 100000
Слайд 88Сочетания
Сочетанием из n элементов по m ( m ≤ n) называется
Формула (число размещений «из эн по эм»):
Сочетания – конечные множества, в которых порядок не имеет значения.
Слайд 89Решение. (обратить внимание на его оформление!)
Основное множество: {мак, роза, тюльпан, лилия,
Соединение – букет из трех цветков ⇒
Проверим, важен ли порядок:
{тюльпан, лилия, гвоздика} и {лилия, тюльпан, гвоздика} – один и тот же букет ⇒ порядок неважен ⇒ это подмножество ⇒ это сочетание «из пяти по три».
Ответ: 10 букетов
Сочетания
Пример 10. Сколькими способами можно составить букет из 3 цветов, если в вашем распоряжении 5 цветов: мак, роза, тюльпан, лилия, гвоздика?
Слайд 90Сочетания с повторениями
Сочетаниями с повторениями из m по n называют соединения,
Число сочетаний из m по n
обозначают
Слайд 91Сочетания с повторениями
Если из множества, содержащего n элементов, выбирается поочередно m элементов, причём выбранный элемент
Сочетания с повторениями














![Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕПримерМножество натуральных чисел бесконечно.ПримерМножество точек отрезка [0;1] бесконечно.ПримерМножество](/img/tmb/1/23795/9f10c3ec29c28e56fda417365d3b8246-800x.jpg)