- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОГЭ 2018. Модуль Геометрия презентация
Содержание
- 1. ОГЭ 2018. Модуль Геометрия
- 2. Характеристика модуля: Модуль «Геометрия» состоит из 2-х
- 3. Задание 25. Задание 26. Автор: Фролова Л.А.
- 4. Часть 1 Автор: Фролова Л.А.
- 5. Задание 15 Характеристика задания: задание 15 ОГЭ
- 6. Пример задания Автор: Фролова Л.А.
- 7. Задание 16 Характеристика задания: задание 15 ОГЭ
- 8. Напомним основные факты, связанные с треугольниками:
- 9. Автор: Фролова Л.А.
- 10. Пример задания Автор: Фролова Л.А.
- 11. Задание 17 Характеристика задания: задание 16 ОГЭ
- 12. — две окружности не имеют общих точек
- 13. Автор: Фролова Л.А.
- 14. Задание 18 Автор: Фролова Л.А.
- 15. Автор: Фролова Л.А.
- 16. Автор: Фролова Л.А.
- 17. Автор: Фролова Л.А.
- 18. Задание 19 Автор: Фролова Л.А.
- 19. Автор: Фролова Л.А.
- 20. Задание 20 Характеристика задания: одного или нескольких
- 21. Пример задания Укажите в порядке возрастания без
- 22. Часть 2 Автор: Фролова Л.А.
- 23. Задание 24 Характеристика задания: задание 24 ОГЭ
- 24. Автор: Фролова Л.А.
- 25. Задание 25 Характеристика задания: задание 25 ОГЭ
- 26. Автор: Фролова Л.А.
- 27. Задание 26 Характеристика задания:26-е задание ОГЭ по
- 28. Автор: Фролова Л.А.
- 29. Шкала пересчёта суммарного балла за выполнение модуля
Слайд 2Характеристика модуля:
Модуль «Геометрия» состоит из 2-х частей.
Часть 1. 6 заданий
Каждое задание оценивается в 1 балл.
Часть 2. 3 задания (24-26) с развёрнутым ответом.
Задание 24.
Автор: Фролова Л.А.
Слайд 5Задание 15
Характеристика задания: задание 15 ОГЭ по математике представляет собой практическую
Автор: Фролова Л.А.
Слайд 7Задание 16
Характеристика задания: задание 15 ОГЭ по математике открывает блок геометрических
Методические рекомендации с разбором задач сторон прямоугольного треугольника по двум другим его сторонам, понимать, что такое равнобедренный и равносторонний треугольники, и уметь применять их простейшие свойства к решению задач.
Автор: Фролова Л.А.
Слайд 8Напомним основные факты, связанные с треугольниками:
— сумма углов треугольника равна
— внешний угол треугольника равен сумме двух не смежных с ним внутренних углов треугольника;
— высоты треугольника пересекаются в одной точке;
— биссектрисы треугольника пересекаются в одной точке (эта точка является центром вписанной окружности треугольника);
— серединные перпендикуляры к сторонам треугольника пересекаются в одной точке (эта точка является центром описанной окружности треугольника);
— медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершин треугольника;
— средняя линия треугольника параллельна одной из его сторон и равна её половине.
Автор: Фролова Л.А.
Слайд 11Задание 17
Характеристика задания: задание 16 ОГЭ по математике представляет собой задачу,
Приведём основные факты по теме «Окружность и круг:
— центральный угол окружности измеряется дугой этой окружности, на которую он опирается;
— вписанный угол окружности равен половине центрального угла и измеряется половиной дуги, на которую он опирается;
— вписанный угол, опирающийся на диаметр окружности, равен 90◦ ;
— касательная к окружности перпендикулярна радиусу этой окружности, проведённому в точку касания;
— отрезки касательных, проведённых к окружности из одной точки, равны;
— центр окружности, вписанной в угол, лежит на биссектрисе этого угла;
— угол между двумя секущими к окружности, пересекающимися внутри окружности, равен полусумме дуг, высекаемых на окружности вертикальными углами, образованными этими секущими;
— угол между двумя секущими к окружности, пересекающимися вне окружности, равен полуразности дуг, высекаемых на окружности углом, образованным этими секущими;
Автор: Фролова Л.А.
Слайд 12— две окружности не имеют общих точек в том и только
— две окружности имеют ровно две общие точки (пересекаются в двух точках) в том и только том случае, если расстояние между их центрами меньше суммы радиусов этих окружностей, но больше разности большего и меньшего радиусов;
— две окружности имеют ровно одну общую точку (касаются) в том и только том случае, если расстояние между их центрами равно сумме радиусов этих окружностей (внешнее касание) либо равно разности большего и меньшего радиусов этих окружностей (внутреннее касание);
— длина окружности равна 2πr, где r — радиус окружности;
— площадь круга равна πr 2 , где r — радиус круга.
Автор: Фролова Л.А.
Слайд 20Задание 20
Характеристика задания: одного или нескольких верных утверждений из множества данных
Автор: Фролова Л.А.
Слайд 21Пример задания
Укажите в порядке возрастания без пробелов, запятых и прочих символов
Существует параллелограмм, диагонали которого равны.
В любом параллелограмме диагонали различны.
Существует ромб, диагонали которого равны.
4) В любом ромбе диагонали различны.
5) Существует трапеция, диагонали которой равны.
6) В любой трапеции диагонали различны.
Р е ш е н и е.
Первое и третье утверждения являются верными, примером в обоих случаях является квадрат. Поэтому второе и четвёртое утверждения ложны. Пятое утверждение верно, примером является равнобедренная трапеция. Следовательно, шестое утверждение ложно.
Ответ: 135.
Автор: Фролова Л.А.
Слайд 23Задание 24
Характеристика задания: задание 24 ОГЭ по математике открывает условный блок
Автор: Фролова Л.А.
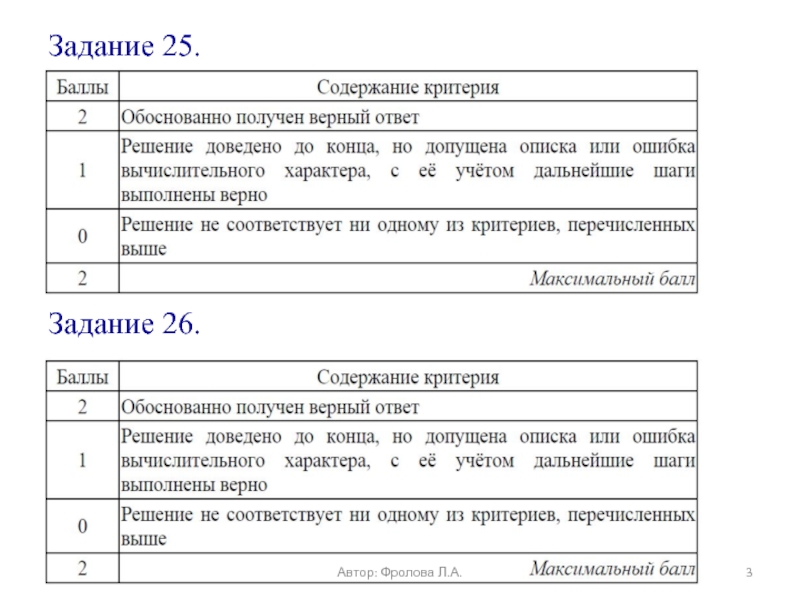
Слайд 25Задание 25
Характеристика задания: задание 25 ОГЭ по математике представляет собой планиметрическую
Автор: Фролова Л.А.
Слайд 27Задание 26
Характеристика задания:26-е задание ОГЭ по математике представляет собой планиметрическую задачу
Автор: Фролова Л.А.
Слайд 29Шкала пересчёта суммарного балла за выполнение модуля «ГЕОМЕТРИЯ» в отметку по
«2» - 0-2 баллов
«3» - 3 – 4 баллов;
«4» - 5 – 7 баллов;
«5» - 8 – 12 баллов.
Автор: Фролова Л.А.