- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обчислення обємів просторових тіл з допомогою інтеграла презентация
Содержание
- 1. Обчислення обємів просторових тіл з допомогою інтеграла
- 2. I. Обєм прямокутного паралелепіпеда з
- 3. II. Обєм прямої призми з висотою
- 4. III. Обєм n-кутної прямої призми
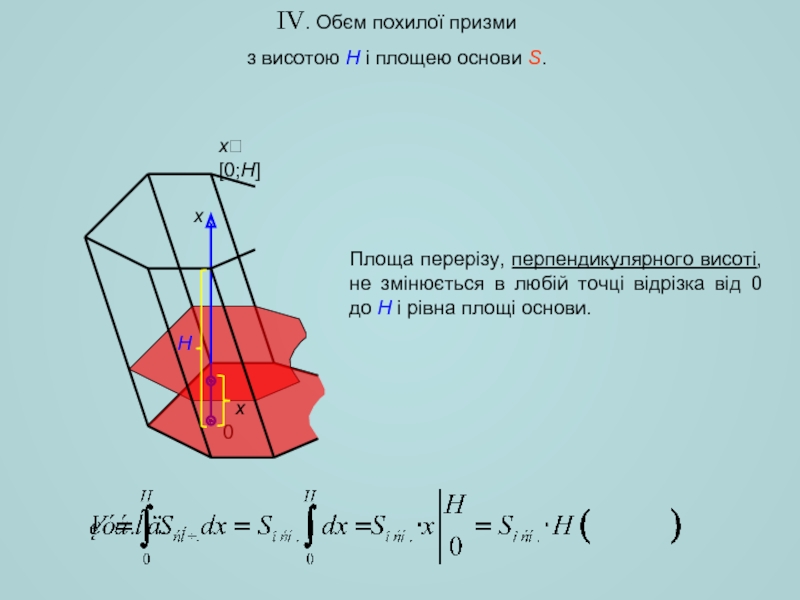
- 5. IV. Обєм похилої призми з висотою
- 6. V. Обєм трикутної піраміди з висотою H
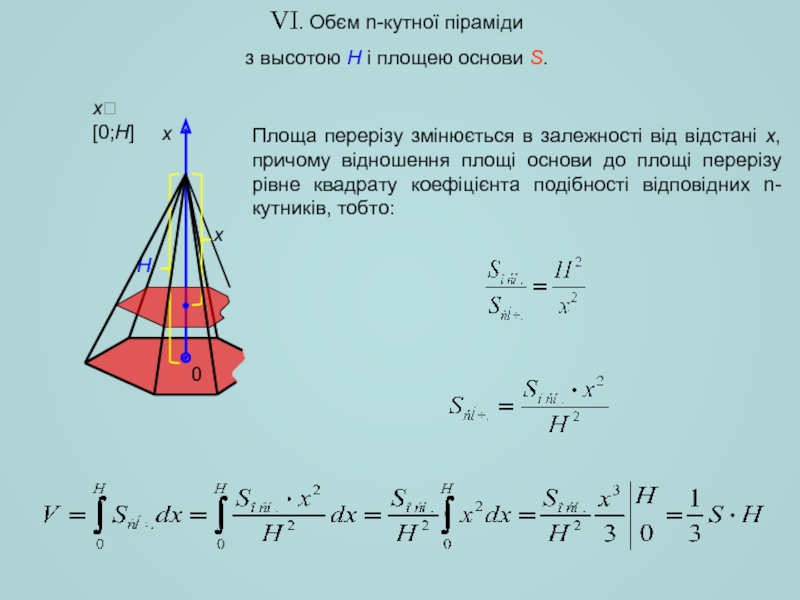
- 7. VI. Обєм n-кутної піраміди з высотою
- 8. VII. Обєм циліндра з висотою H
- 9. VIII. Об’єм конуса з висотою
- 10. IX. Обєм кулі з радіусом R. Знайдемо
- 11. X. Обєм кульового сегмента.
I. Обєм прямокутного паралелепіпеда з висотою H і площею основи S. x H x[0;H] 0 Площа перерізу не змінюється в любій точці відрізка від 0 до H і рівна
Слайд 2
I. Обєм прямокутного паралелепіпеда
з висотою H і площею основи S.
x
H
x[0;H]
0
Площа перерізу
не змінюється в любій точці відрізка від 0 до H і рівна площі основи.
x
Слайд 3
II. Обєм прямої призми
з висотою H і площею основи S.
x
x[0;H]
H
0
Площа перерізу
не змінюється в любій точці відрізка від 0 до H і рівна площі основи.
x
Слайд 4
III. Обєм n-кутної прямої призми
з висотою H і площею основи
S.
x
x[0;H]
H
0
Площа перерізу не змінюється в любій точці відрізка від 0 до H і рівна площі основи.
x
Слайд 5IV. Обєм похилої призми
з висотою H і площею основи S.
Площа
перерізу, перпендикулярного висоті, не змінюється в любій точці відрізка від 0 до H і рівна площі основи.
x
H
x[0;H]
0
x
Слайд 6V. Обєм трикутної піраміди
з висотою H і площею основи S.
H
x
x[0;H]
⇒
x
Площа перерізу
змінюється в залежності від відстані x, причому відношення площі основи до площі перерізу рівне квадрату коефіцієнта подібності відповідних трикутників, тобто:
0
Слайд 7
VI. Обєм n-кутної піраміди
з высотою H і площею основи S.
H
x
Площа перерізу
змінюється в залежності від відстані x, причому відношення площі основи до площі перерізу рівне квадрату коефіцієнта подібності відповідних n-кутників, тобто:
x
x[0;H]
0
Слайд 8
VII. Обєм циліндра з висотою H і площею основи S.
x
x[0;H]
H
0
x
Площа перерізу
не змінюється в любій точці відрізка від 0 до H і рівна площі основи.
Слайд 9
VIII. Об’єм конуса з висотою H і площею основи S.
x
x[0;H]
H
x
Площа
перерізу змінюється в залежності від відстані x, причому відношення площі основи до площі перерізу рівне квадрату коефіцієнта подібності відповідних кругів, тобто:
0
Слайд 10IX. Обєм кулі з радіусом R.
Знайдемо обєм півкулі, як нескінченну інтегральну
суму площ перерізів з радіусом r, де:
R
x
Значить, обєм всієї кулі рівний:
x
0
r
Слайд 11X. Обєм кульового сегмента.
Виведення формули обєму кульового сегмента з висотою h
і радіусом основи r відрізняється від виведення обєму півкулі нижньою границею інтегрування. В даному випадку вона рівна R –h :
r
R
h
x
Зверніть увагу, що в формулі обєму кульового сегмента використовується радіус кулі (R), а не радіус основи сегмента (r)!
