- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нестандартные способы решения тригонометрических уравнений презентация
Содержание
- 1. Нестандартные способы решения тригонометрических уравнений
- 2. Основные цели: освоить способы создания
- 3. Задачи: Использовать современные информационные технологии в ходе
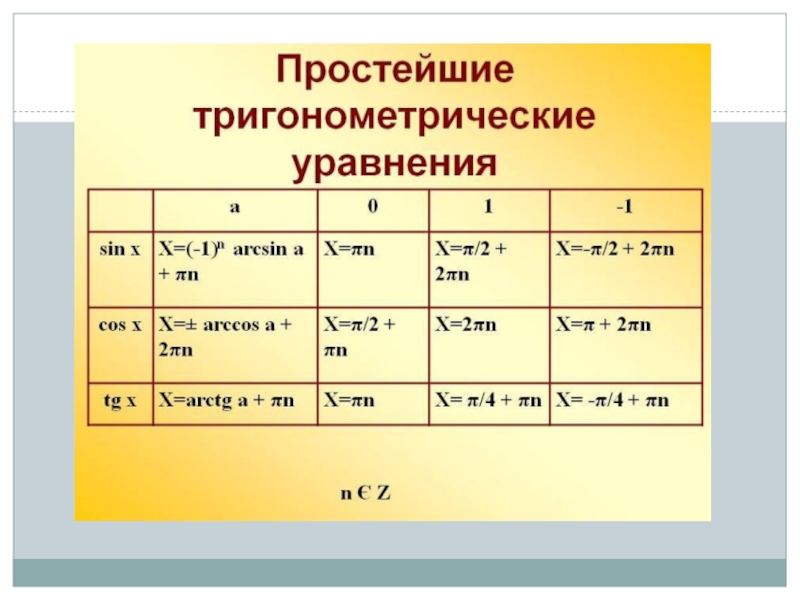
- 4. Введение Решение тригонометрического уравнения состоит из двух
- 5. Ее возможности: Построение кривых: Построение графиков
- 6. Построение графика
- 7. Далее для построения второй функции вводим:
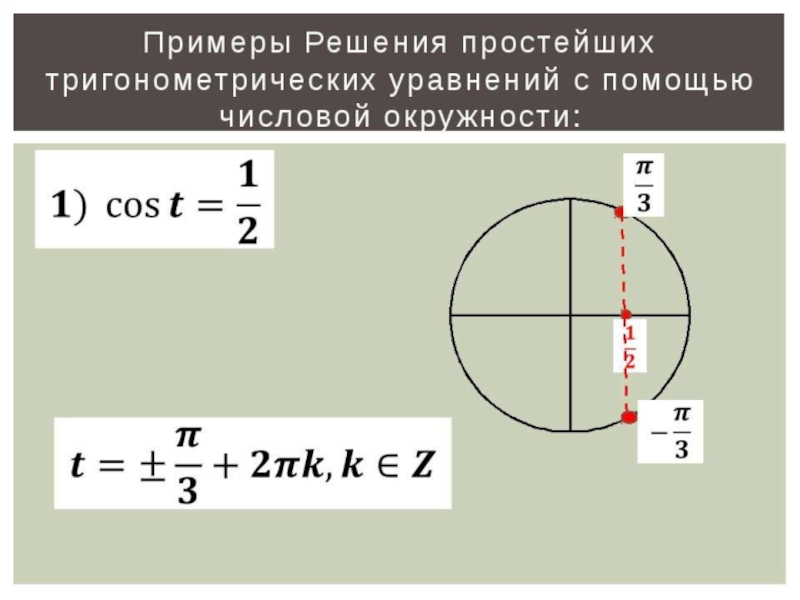
- 8. Отработка практических навыков. Задание №1 Необходимо решить
- 9. 2. Аналогично решаем и второе уравнение. В
- 11. Решим это задание графическим методом, опираясь на полученные знания.
- 13. Нам необходимо построить два графика: и y
- 14. Миноносец «Боевой» Аналогичным способом решаем эту задачу.
- 15. Практические\корабль красных.ggb Построив графики, мы сразу видим
- 18. Задание № 3. Создание динамической модели. Задание.
- 19. При изменении любого из этих коэффициентов изменяется
- 20. Основные выводы работа с программой GeoGebra
Слайд 1ВЫПОЛНИЛА:
ИВАНОВА СВЕТЛАНА
УЧЕНИЦА 10 КЛАССА
Тема: «Нестандартные способы решения тригонометрических уравнений
Слайд 2
Основные цели:
освоить способы создания динамических чертежей с помощью программы GeoGebra;
изучить
Освоить простейшие тригонометрические уравнения;
отработать технологию решения тригонометрических уравнений графическим способом с помощью динамической программы GeoGebra;
Слайд 3Задачи:
Использовать современные информационные технологии в ходе решения математических задач.
Отработать алгоритм решения
Выработать прочные навыки решения простейших тригонометрических уравнений графическим способом;
Рационально подходить к выбору прикладных программ для решения поставленных задач.
Развивать логическое мышление, память, математическую речь.
Слайд 4Введение
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения
В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд».
Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников.
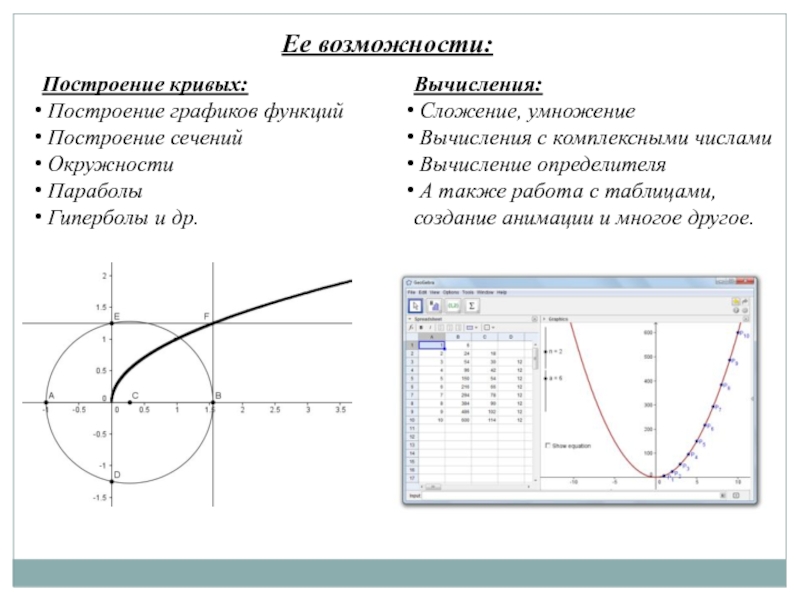
Слайд 5Ее возможности:
Построение кривых:
Построение графиков функций
Построение сечений
Окружности
Параболы
Гиперболы
Вычисления:
Сложение, умножение
Вычисления с комплексными числами
Вычисление определителя
А также работа с таблицами, создание анимации и многое другое.
Слайд 6
Построение графика функции y= sin x
Построение графика функции y= cos x
Преобразования
Преобразования графика функции y= cos x
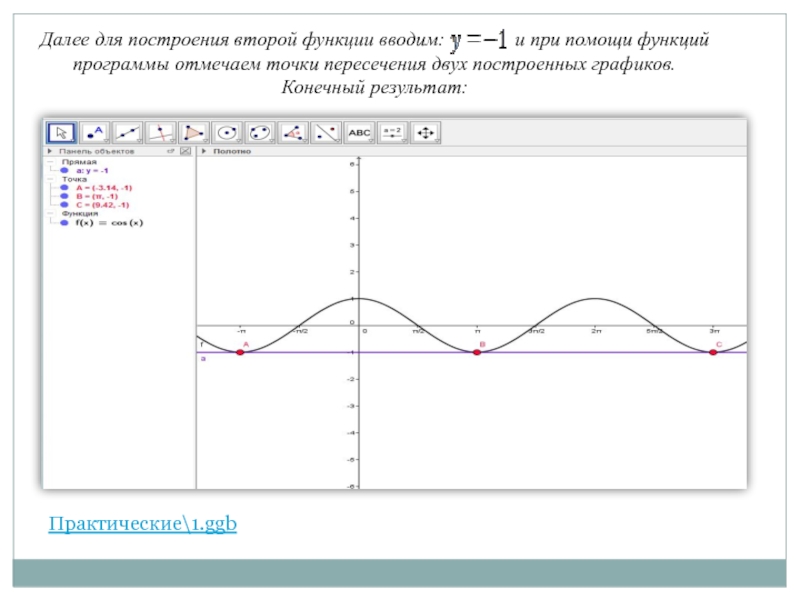
Слайд 7Далее для построения второй функции вводим:
Конечный результат:
Практические\1.ggb
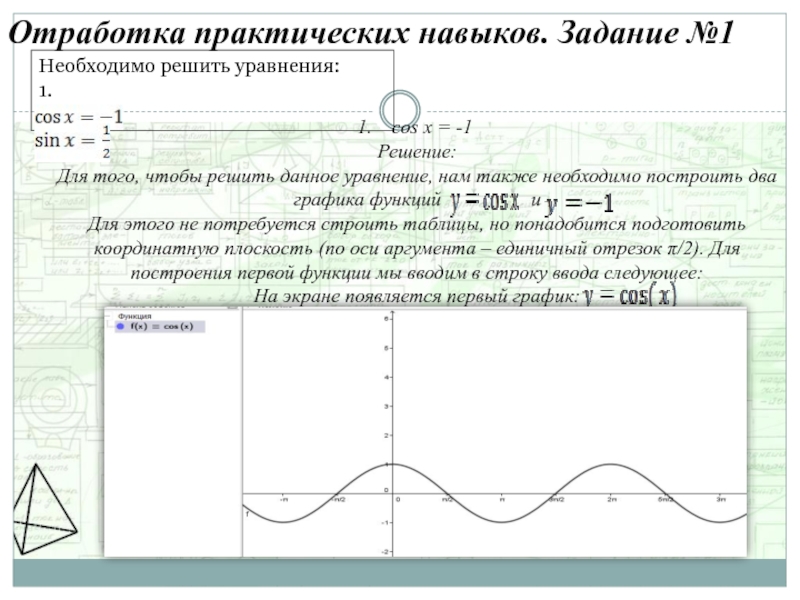
Слайд 8Отработка практических навыков. Задание №1
Необходимо решить уравнения:
1.
2.
cos x = -1
Решение:
Для того,
Для этого не потребуется строить таблицы, но понадобится подготовить координатную плоскость (по оси аргумента – единичный отрезок π/2). Для построения первой функции мы вводим в строку ввода следующее:
На экране появляется первый график:
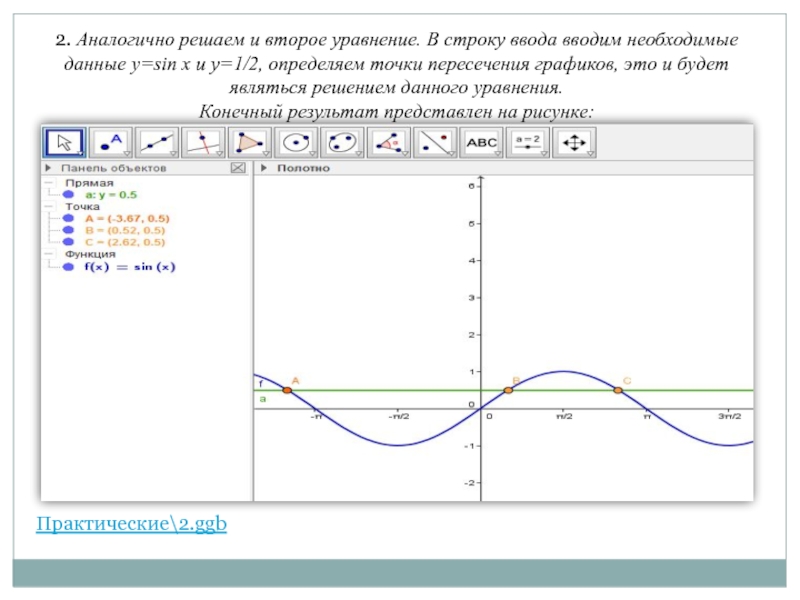
Слайд 92. Аналогично решаем и второе уравнение. В строку ввода вводим необходимые
Конечный результат представлен на рисунке:
Практические\2.ggb
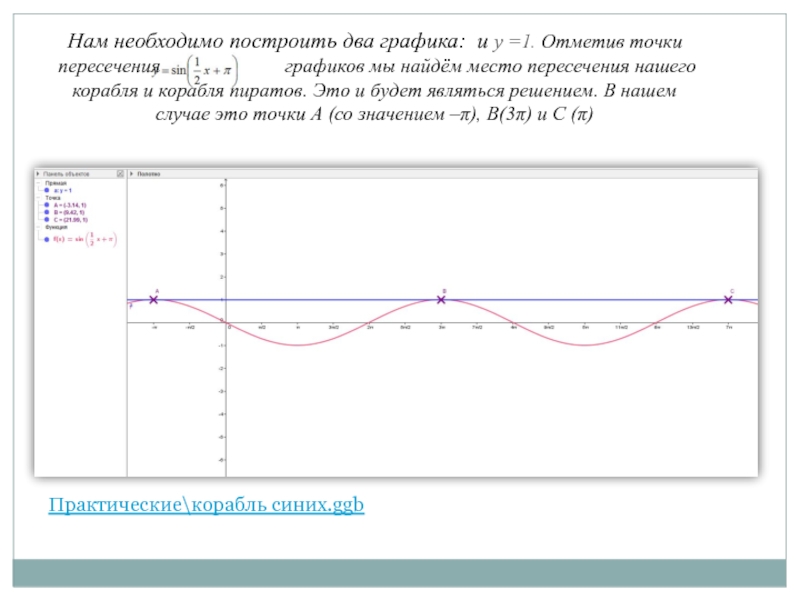
Слайд 13Нам необходимо построить два графика: и y =1. Отметив точки
Практические\корабль синих.ggb
Слайд 14Миноносец «Боевой»
Аналогичным способом решаем эту задачу. В строку ввода вводим заданные
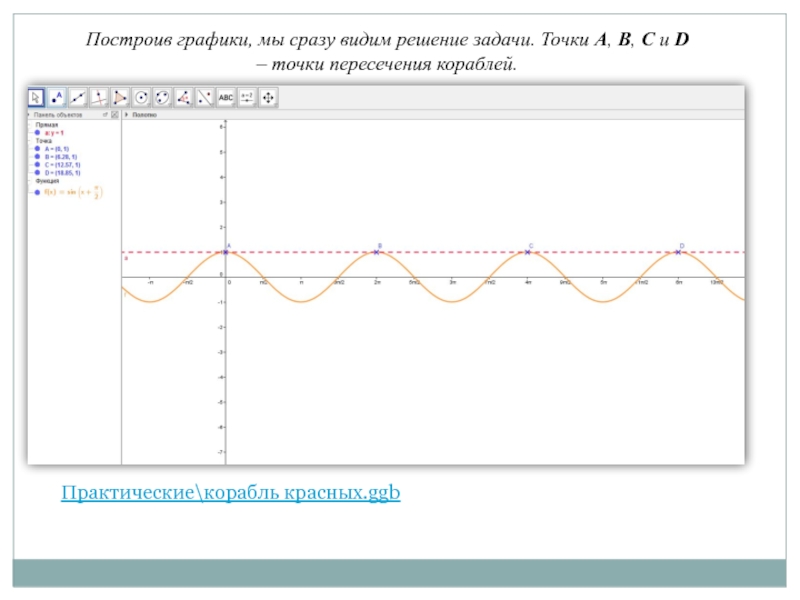
Слайд 15Практические\корабль красных.ggb
Построив графики, мы сразу видим решение задачи. Точки А, В,
Слайд 18Задание № 3. Создание динамической модели.
Задание. Создать динамическую модель для иллюстрации
Для выполнения этого типа задания нам потребуются ползунки, которые отвечают за динамическое изменение параметров функции при различных значениях в режиме реального времени.
Для начала рисуем график квадратичной функции (вводим формулу в строку ввода в соответствии с синтаксисом программы), затем создаем ползунки для параметров a, b и c.
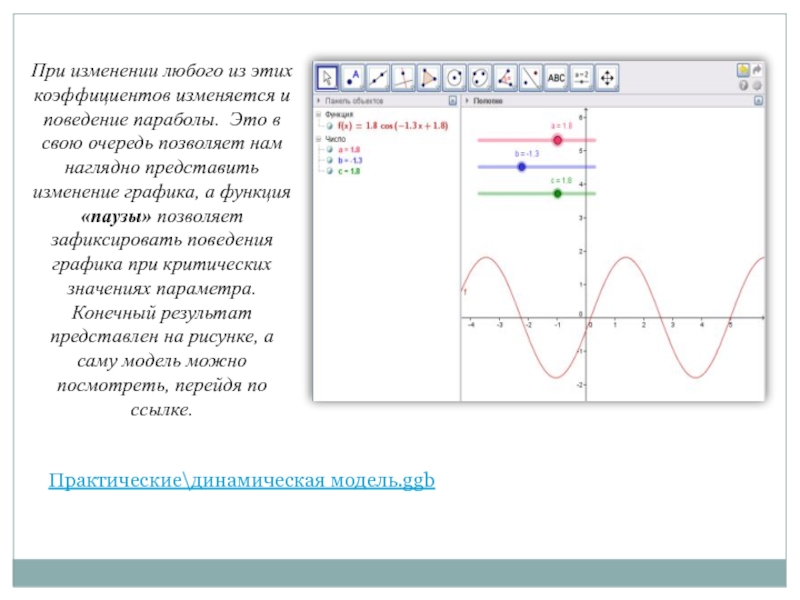
Слайд 19При изменении любого из этих коэффициентов изменяется и поведение параболы. Это
Конечный результат представлен на рисунке, а саму модель можно посмотреть, перейдя по ссылке.
Практические\динамическая модель.ggb
Слайд 20Основные выводы
работа с программой GeoGebra в динамическом режиме активизирует сильных
работа с программой GeoGebra очень удобна для демонстрации трудностей, возникающих при использовании графического метода решения задач с параметрами;
Освоили методы простейшего решения тригонометрических уравнений;
работа с программой GeoGebra требует минимального уровня информационно-компьютерной грамотности учителя и учащихся и разумных временных затрат для получения желаемого результата.