- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Несобственный интеграл презентация
Содержание
- 1. Несобственный интеграл
- 2. определение несобственного интеграла несобственный интеграл
- 3. Определение несобственного интеграла Интеграл называется несобственным,
- 4. Несобственный интеграл первого рода Пусть
- 5. Пример Вычислить несобственный интеграл: Несобственный интеграл расходится, и площадь закрашенной криволинейной трапеции равна бесконечности
- 6. Пример Вычислить несобственный интеграл: Площадь закрашенной
- 7. Несобственный интеграл второго рода Пусть функция
- 8. Пример Добавка +0 означает, что мы
- 9. Пример Вычислим: Если подынтегральная функция не
- 10. Спасибо за внимание!
Слайд 1Подготовил: студент группы П-144 Сукиасян А.А
Лектор: Маринченко Елена Викторовна
НЕСОБСТВЕННЫЙ
ИНТЕГРАЛ
Слайд 2
определение несобственного интеграла
несобственный интеграл по неограниченному промежутку
пример
несобственный интеграл от неограниченной
пример
Содержание
Слайд 3Определение несобственного интеграла
Интеграл называется несобственным, если:
Один или оба его предела бесконечны
Подынтегральная функция имеет точки разрыва
И то, и другое вместе
Слайд 4Несобственный интеграл первого рода
Пусть функция f(x) определена на промежутке [a,∞)
- формула Ньютона-Лейбница
Формула Ньютона-Лейбница для несобственного интеграла
Если предел конечен, то несобственный интеграл называется сходящимся, иначе - расходящимся
Слайд 5Пример
Вычислить несобственный интеграл:
Несобственный интеграл расходится, и площадь закрашенной криволинейной трапеции равна
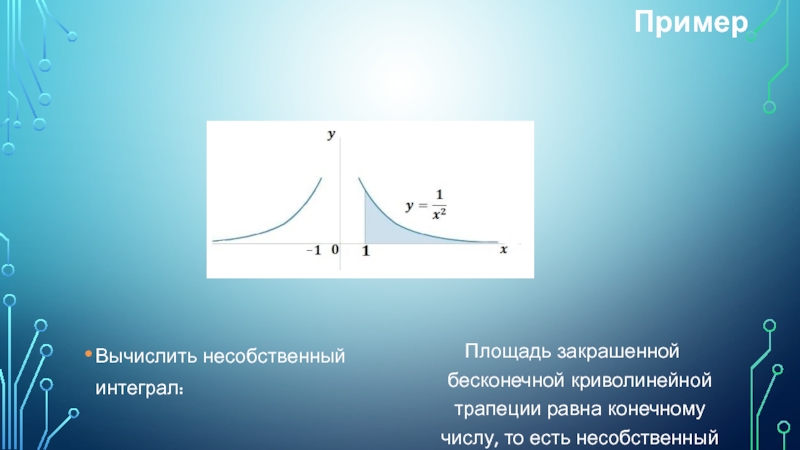
Слайд 6Пример
Вычислить несобственный интеграл:
Площадь закрашенной бесконечной криволинейной трапеции равна конечному числу, то
Слайд 7Несобственный интеграл второго рода
Пусть функция f(x) непрерывна на промежутке [a,b) и
В отличие от определенного интеграла, в несобственном интеграле подынтегральная функция f(x) не существует в одном из следующих случаев:
в точке x = a
в точке x = b
в обеих точках сразу
на отрезке интегрирования
Слайд 8Пример
Добавка +0 означает, что мы стремимся к значению ½ справа
Знак минус
Найдём неопределенный интеграл:
Вычислим несобственный интеграл:
Если подынтегральная функция не существует в точке x=a: