Неравенства и системы неравенств с двумя переменными презентация

Содержание

1. Неравенства и системы неравенств с двумя переменными
2. Девиз урока Да, надо математику любить И
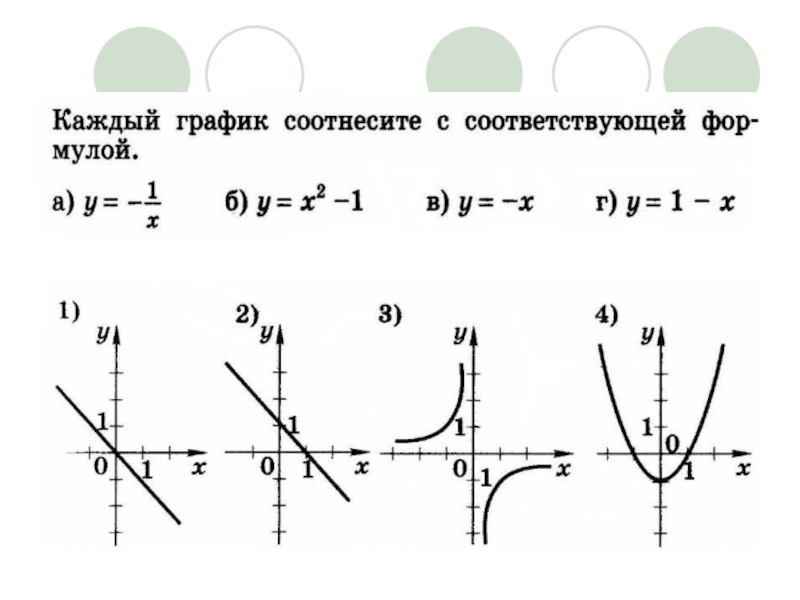
3. Опишите графическую модель уравнения
5. Какая из пар (х; у) является решением
6. Решением какой системы уравнений является пара чисел (2;3)?
7. Какая из пар чисел (x;y) является решением
8. Опишите алгоритм решения системы уравнений графическим методом
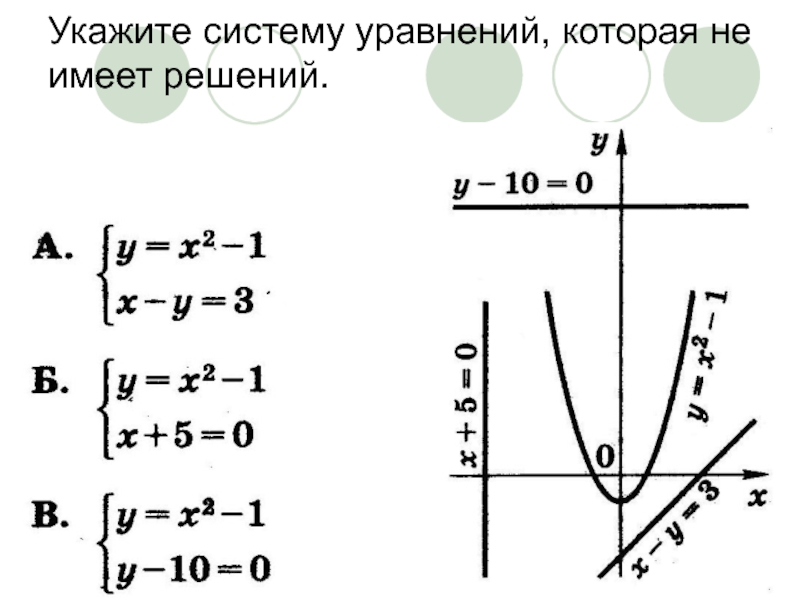
9. Укажите систему уравнений, которая не имеет решений.
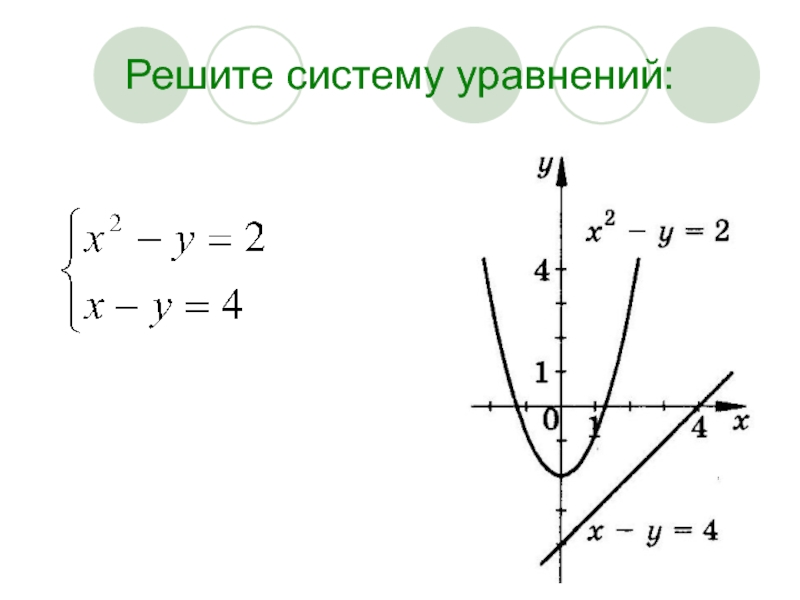
10. Решите систему уравнений:
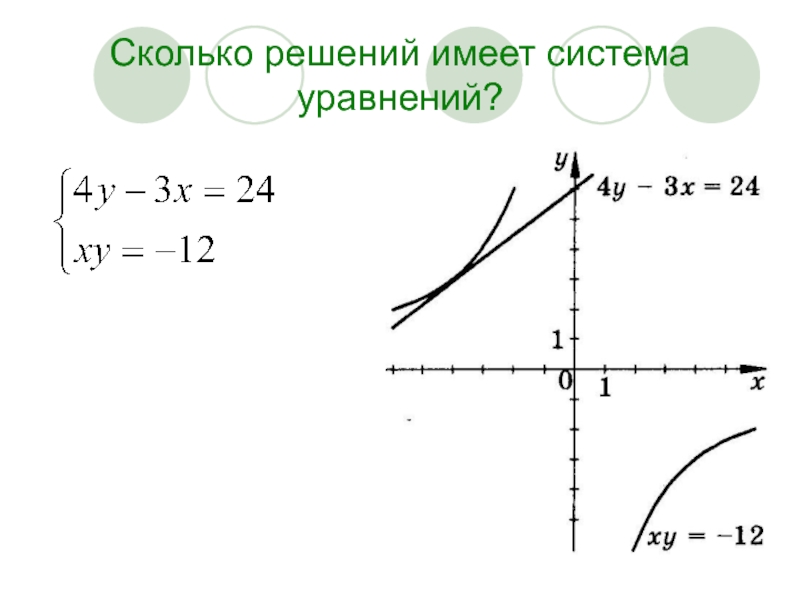
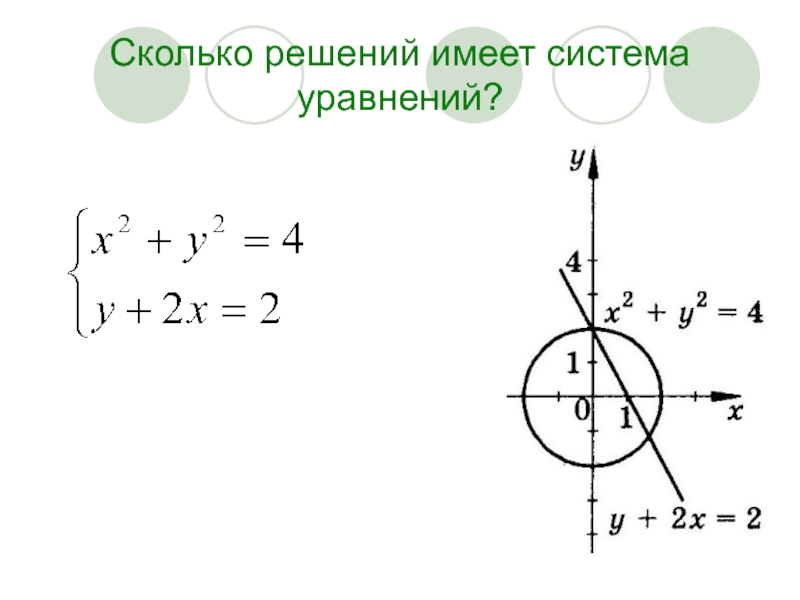
11. Сколько решений имеет система уравнений?
12. Сколько решений имеет система уравнений?
13. Если уравнение р(х; у) = 0 удаётся
14. Решения неравенства изображаются точками плоскости, расположенными по
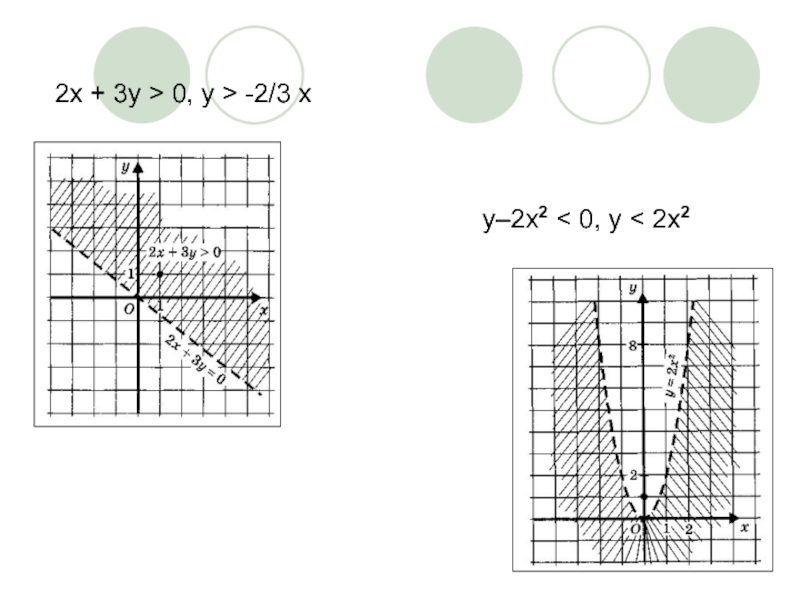
15. 2х + 3у > 0, у >
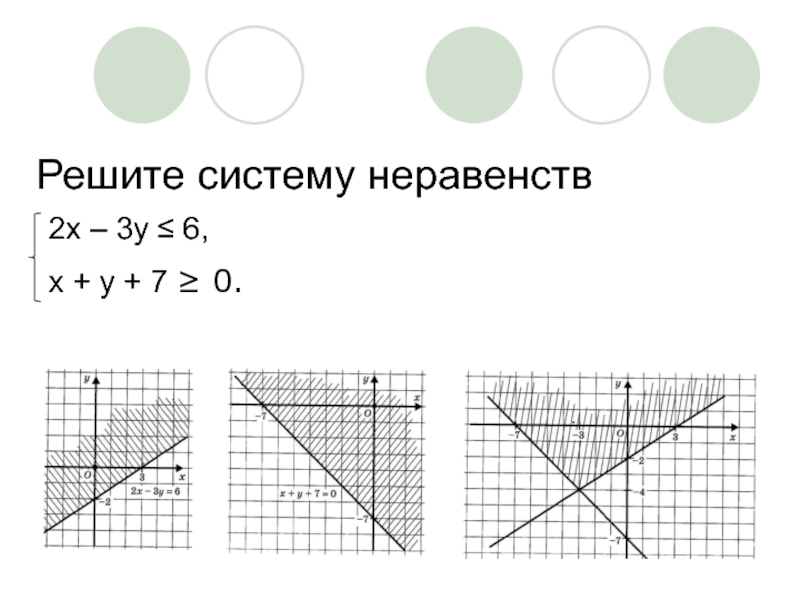
16. Решите систему неравенств 2x – 3y ≤
17. Математический диктант
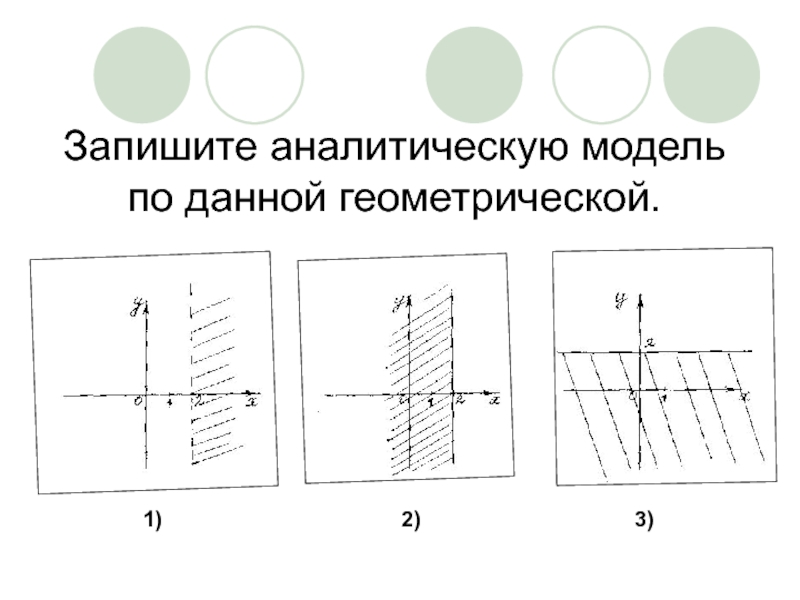
18. Запишите аналитическую модель по данной геометрической. 1) 2) 3)
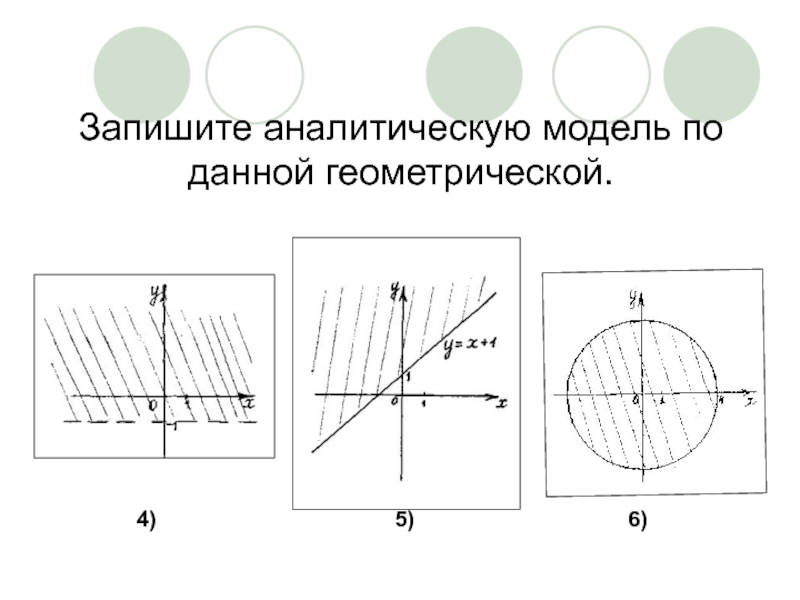
19. Запишите аналитическую модель по данной геометрической. 4) 5) 6)
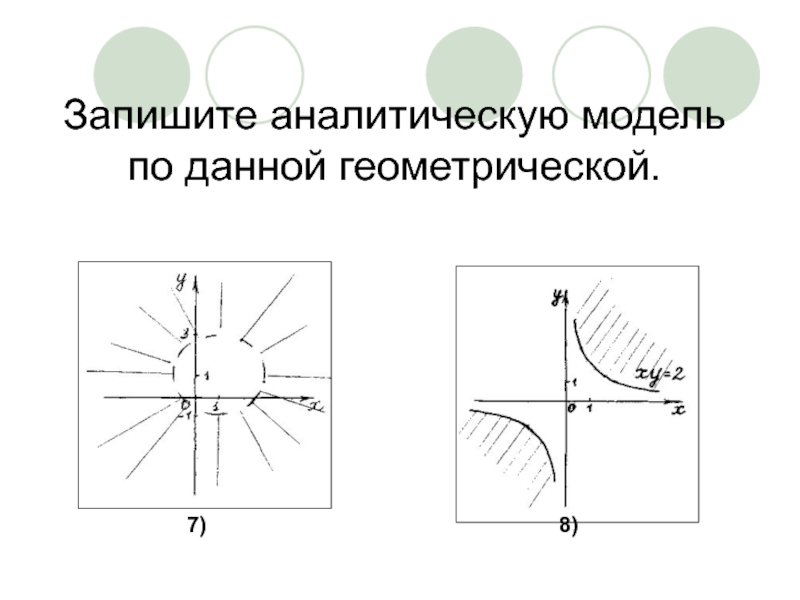
20. Запишите аналитическую модель по данной геометрической. 7) 8)
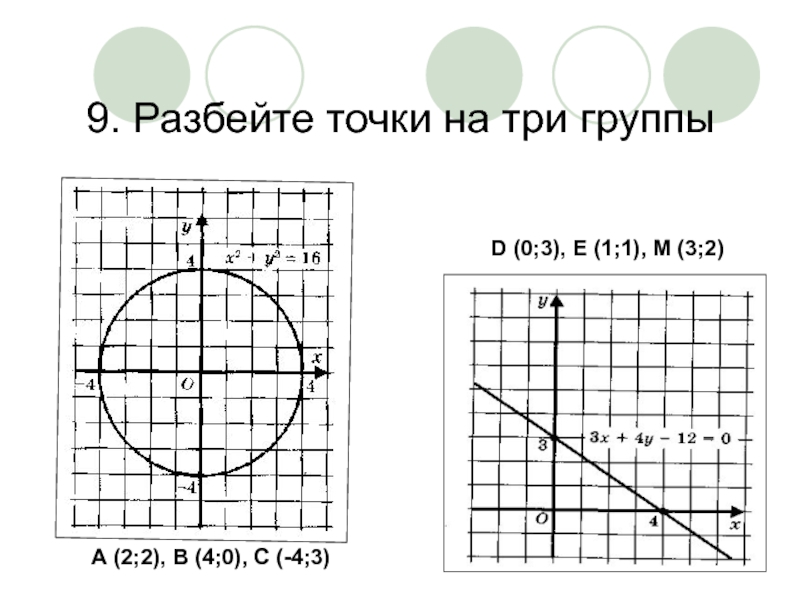
21. 9. Разбейте точки на три группы А
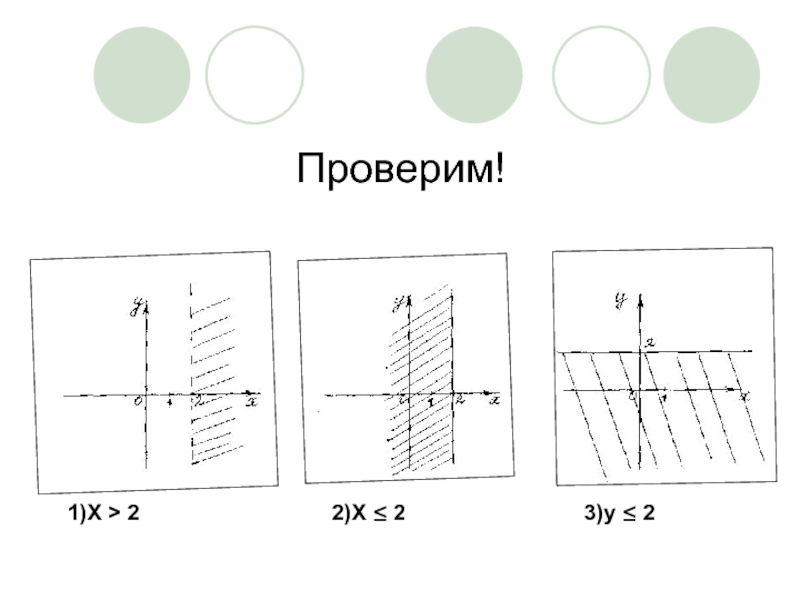
22. Проверим! 1)X > 2 2)X ≤ 2 3)y ≤ 2
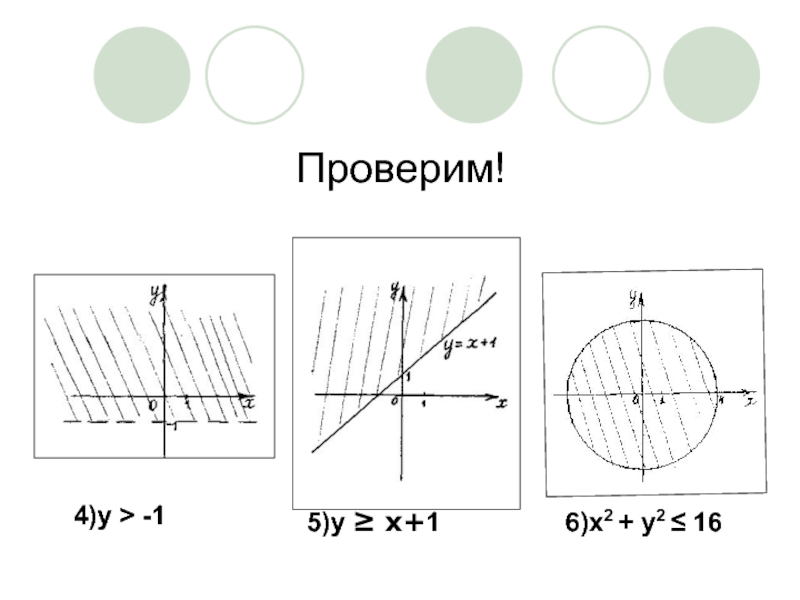
23. Проверим! 4)y > -1 5)y ≥ x+1 6)x2 + y2 ≤ 16
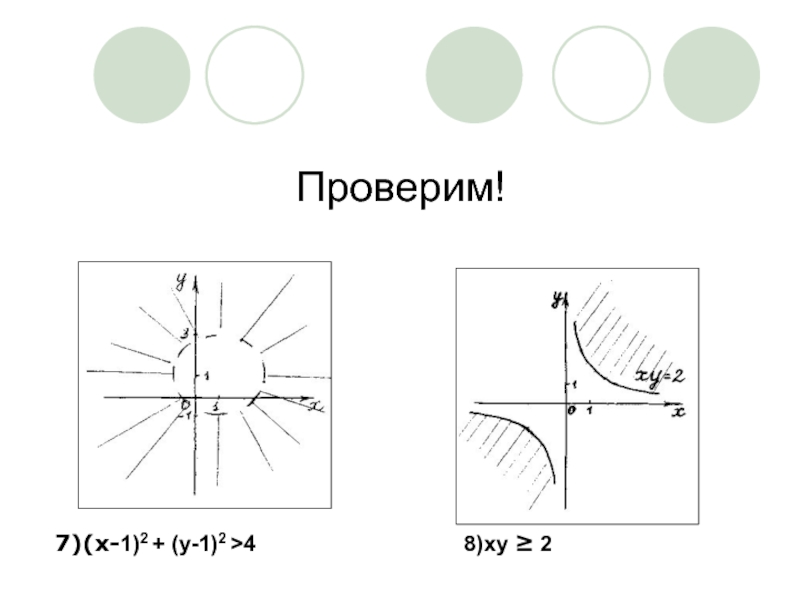
24. Проверим! 7)(x-1)2 + (y-1)2 >4 8)xy ≥ 2
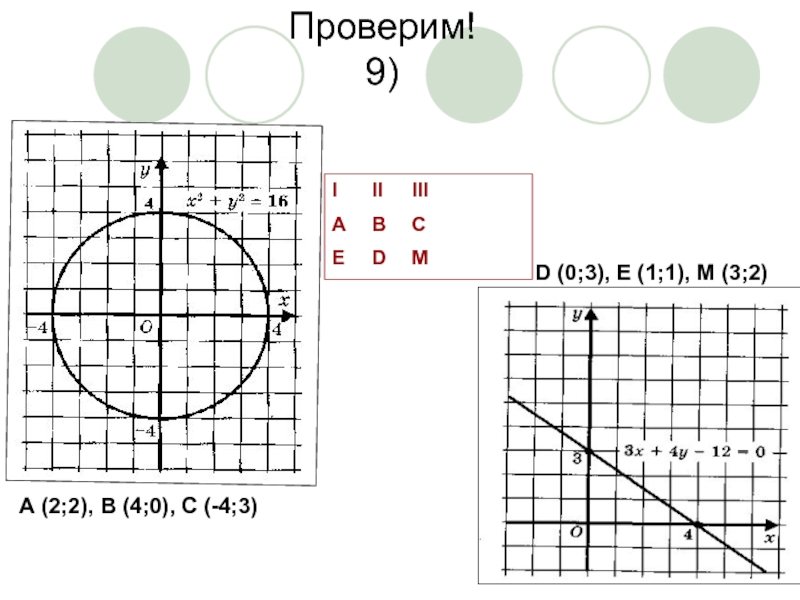
25. Проверим! 9) А (2;2), В (4;0),
26. Критерии оценки Задания №1 - №4 –
27. Ну, кто говорил, что все

Девиз урока Да, надо математику любить И не считать ученье за мученье! Все в жизни пригодится, ты учись, Учись и не жалей на то мгновенье!

Главная
Математика
Неравенства и системы неравенств с двумя переменными

Слайд 1Неравенства и системы неравенств с двумя переменными

Неравенства и системы неравенств с

двумя переменными

Слайд 2Девиз урока
Да, надо математику любить
И не считать ученье за мученье!
Все в

жизни пригодится, ты учись,
Учись и не жалей на то мгновенье!

Слайд 3

Опишите графическую модель уравнения

Слайд 4

Слайд 5Какая из пар (х; у) является решением

:
а) (1; 2);

б) (2; 1)?

Слайд 6Решением какой системы уравнений является пара чисел (2;3)?

Слайд 7Какая из пар чисел (x;y) является решением системы неравенств
2x - 3y

≤ 6,
x + y + 7 >0:

а) (2;1) б) (3;-2)?

Слайд 8Опишите алгоритм решения системы уравнений графическим методом

Слайд 9Укажите систему уравнений, которая не имеет решений.

Слайд 10Решите систему уравнений:

Слайд 11Сколько решений имеет система уравнений?

Слайд 12Сколько решений имеет система уравнений?

Слайд 13Если уравнение р(х; у) = 0 удаётся преобразовать к виду

у = f(х), то график функции у = f(х) считается одновременно графиком уравнения р(х; у) = 0. Полезно запомнить соответствия:

Если координаты точки то она лежит
К (х; у) удовлетворяют соответственно
неравенству у > f(х) над линией
уравнению у = f(х) на линии
неравенству у < f(х) под линией

Обратное верно

Слайд 14Решения неравенства изображаются точками плоскости, расположенными по одну из сторон от

графика уравнения. Чтобы выбрать нужную часть плоскости, берут в какой-нибудь из них точку, подставляют её координаты в заданное неравенство. Если получается верное числовое неравенство, то часть плоскости выбрана верно, если нет – то нет.

Если графиком рационального уравнения является линия L, то по одну и по другую сторону от L выражение р(х; у) сохраняет постоянный знак.

Слайд 152х + 3у > 0, у > -2/3 х
у–2х2

0, у < 2x2

Слайд 16Решите систему неравенств
2x – 3y ≤ 6,
x + y + 7

≥ 0.

Слайд 17Математический диктант

Слайд 18Запишите аналитическую модель по данной геометрической.
1)
2)
3)

Слайд 19Запишите аналитическую модель по данной геометрической.
4)
5)
6)

Слайд 20Запишите аналитическую модель по данной геометрической.
7)
8)

Слайд 219. Разбейте точки на три группы
А (2;2), В (4;0), С (-4;3)
D

(0;3), Е (1;1), М (3;2)

Слайд 22Проверим!
1)X > 2
2)X ≤ 2
3)y ≤ 2

Слайд 23Проверим!
4)y > -1
5)y ≥ x+1
6)x2 + y2 ≤ 16

Слайд 24Проверим!
7)(x-1)2 + (y-1)2 >4
8)xy ≥ 2

Слайд 25Проверим! 9)
А (2;2), В (4;0), С (-4;3)
D (0;3), Е (1;1), М

(3;2)

I II III
A B C
E D M

Слайд 26Критерии оценки
Задания №1 - №4 – по 1 баллу
Задания №5 -

№8 – по 2 балла
Задание №9 – 3 балла
Оценка «5» - 14-15 баллов
Оценка «4» - 10-12 баллов
Оценка «3» - 8-9 баллов

Слайд 27
Ну, кто говорил, что все сложно, серьезно И что постичь

это все невозможно?

Все оказалось доступным, полезным, а также достаточно интересным!

Скачать презентацию

Неравенства и системы неравенств с двумя переменными презентация

Содержание

Слайд 1Неравенства и системы неравенств с двумя переменными

Неравенства и системы неравенств с

Слайд 2Девиз урока
Да, надо математику любить
И не считать ученье за мученье!
Все в

Слайд 3

Опишите графическую модель уравнения

Слайд 4

Слайд 5Какая из пар (х; у) является решением

:
а) (1; 2);

Слайд 6Решением какой системы уравнений является пара чисел (2;3)?

Слайд 7Какая из пар чисел (x;y) является решением системы неравенств
2x - 3y

Слайд 8Опишите алгоритм решения системы уравнений графическим методом

Слайд 9Укажите систему уравнений, которая не имеет решений.

Слайд 10Решите систему уравнений:

Слайд 11Сколько решений имеет система уравнений?

Слайд 12Сколько решений имеет система уравнений?

Слайд 13Если уравнение р(х; у) = 0 удаётся преобразовать к виду

Слайд 14Решения неравенства изображаются точками плоскости, расположенными по одну из сторон от

Слайд 152х + 3у > 0, у > -2/3 х
у–2х2

Слайд 16Решите систему неравенств
2x – 3y ≤ 6,
x + y + 7

Слайд 17Математический диктант

Слайд 18Запишите аналитическую модель по данной геометрической.
1)
2)
3)

Слайд 19Запишите аналитическую модель по данной геометрической.
4)
5)
6)

Слайд 20Запишите аналитическую модель по данной геометрической.
7)
8)

Слайд 219. Разбейте точки на три группы
А (2;2), В (4;0), С (-4;3)
D

Слайд 22Проверим!
1)X > 2
2)X ≤ 2
3)y ≤ 2

Слайд 23Проверим!
4)y > -1
5)y ≥ x+1
6)x2 + y2 ≤ 16

Слайд 24Проверим!
7)(x-1)2 + (y-1)2 >4
8)xy ≥ 2

Слайд 25Проверим! 9)
А (2;2), В (4;0), С (-4;3)
D (0;3), Е (1;1), М

Слайд 26Критерии оценки
Задания №1 - №4 – по 1 баллу
Задания №5 -

Слайд 27
Ну, кто говорил, что все сложно, серьезно И что постичь

Обратная связь

Что такое ThePresentation.ru?

Неравенства и системы неравенств с двумя переменными презентация

Содержание

Слайд 1Неравенства и системы неравенств с двумя переменнымиНеравенства и системы неравенств с

Слайд 2Девиз урокаДа, надо математику любитьИ не считать ученье за мученье!Все в

Слайд 3Опишите графическую модель уравнения

Слайд 4

Слайд 5Какая из пар (х; у) является решением :а) (1; 2);

Слайд 6Решением какой системы уравнений является пара чисел (2;3)?

Слайд 7Какая из пар чисел (x;y) является решением системы неравенств2x - 3y

Слайд 8Опишите алгоритм решения системы уравнений графическим методом

Слайд 9Укажите систему уравнений, которая не имеет решений.

Слайд 10Решите систему уравнений:

Слайд 11Сколько решений имеет система уравнений?

Слайд 12Сколько решений имеет система уравнений?

Слайд 13Если уравнение р(х; у) = 0 удаётся преобразовать к виду

Слайд 14Решения неравенства изображаются точками плоскости, расположенными по одну из сторон от

Слайд 152х + 3у > 0, у > -2/3 х у–2х2

Слайд 16Решите систему неравенств2x – 3y ≤ 6,x + y + 7

Слайд 17Математический диктант

Слайд 18Запишите аналитическую модель по данной геометрической.1)2)3)

Слайд 19Запишите аналитическую модель по данной геометрической.4)5)6)

Слайд 20Запишите аналитическую модель по данной геометрической.7)8)

Слайд 219. Разбейте точки на три группыА (2;2), В (4;0), С (-4;3)D

Слайд 22Проверим!1)X > 22)X ≤ 23)y ≤ 2

Слайд 23Проверим!4)y > -15)y ≥ x+16)x2 + y2 ≤ 16

Слайд 24Проверим! 7)(x-1)2 + (y-1)2 >48)xy ≥ 2

Слайд 25Проверим! 9)А (2;2), В (4;0), С (-4;3)D (0;3), Е (1;1), М

Слайд 26Критерии оценкиЗадания №1 - №4 – по 1 баллуЗадания №5 -

Слайд 27 Ну, кто говорил, что все сложно, серьезно И что постичь

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Неравенства и системы неравенств с двумя переменными

Неравенства и системы неравенств с

Слайд 2Девиз урока
Да, надо математику любить
И не считать ученье за мученье!
Все в

Слайд 3

Опишите графическую модель уравнения

Слайд 5Какая из пар (х; у) является решением

:
а) (1; 2);

Слайд 7Какая из пар чисел (x;y) является решением системы неравенств
2x - 3y

Слайд 152х + 3у > 0, у > -2/3 х
у–2х2

Слайд 16Решите систему неравенств
2x – 3y ≤ 6,
x + y + 7

Слайд 18Запишите аналитическую модель по данной геометрической.
1)
2)
3)

Слайд 19Запишите аналитическую модель по данной геометрической.
4)
5)
6)

Слайд 20Запишите аналитическую модель по данной геометрической.
7)
8)

Слайд 219. Разбейте точки на три группы
А (2;2), В (4;0), С (-4;3)
D

Слайд 22Проверим!
1)X > 2
2)X ≤ 2
3)y ≤ 2

Слайд 23Проверим!
4)y > -1
5)y ≥ x+1
6)x2 + y2 ≤ 16

Слайд 24Проверим!
7)(x-1)2 + (y-1)2 >4
8)xy ≥ 2

Слайд 25Проверим! 9)
А (2;2), В (4;0), С (-4;3)
D (0;3), Е (1;1), М

Слайд 26Критерии оценки
Задания №1 - №4 – по 1 баллу
Задания №5 -

Слайд 27
Ну, кто говорил, что все сложно, серьезно И что постичь