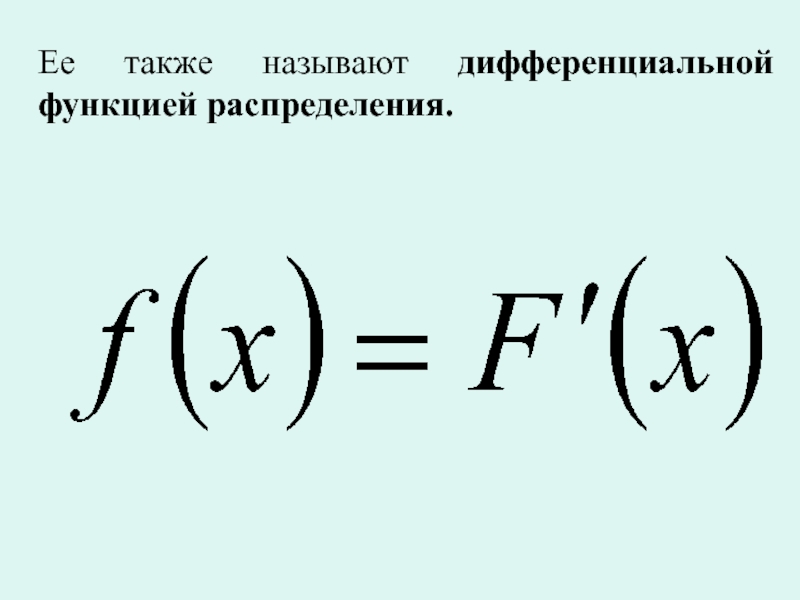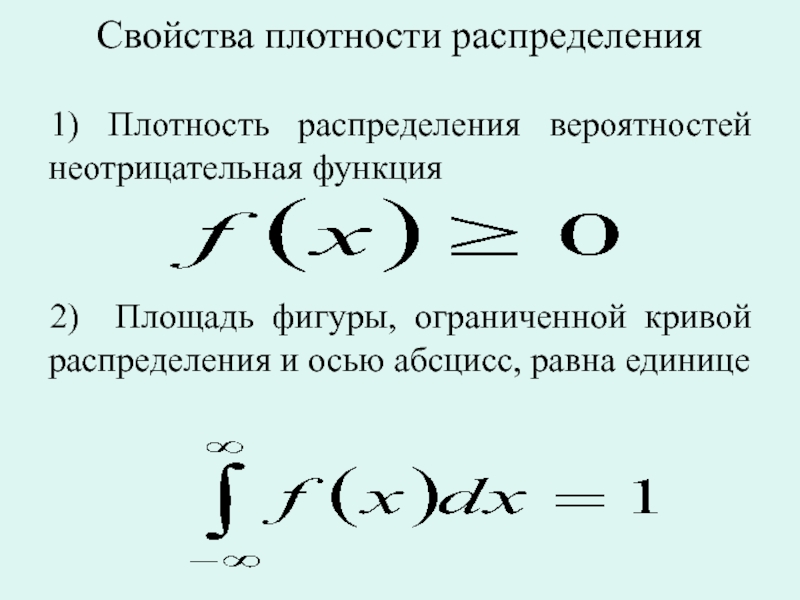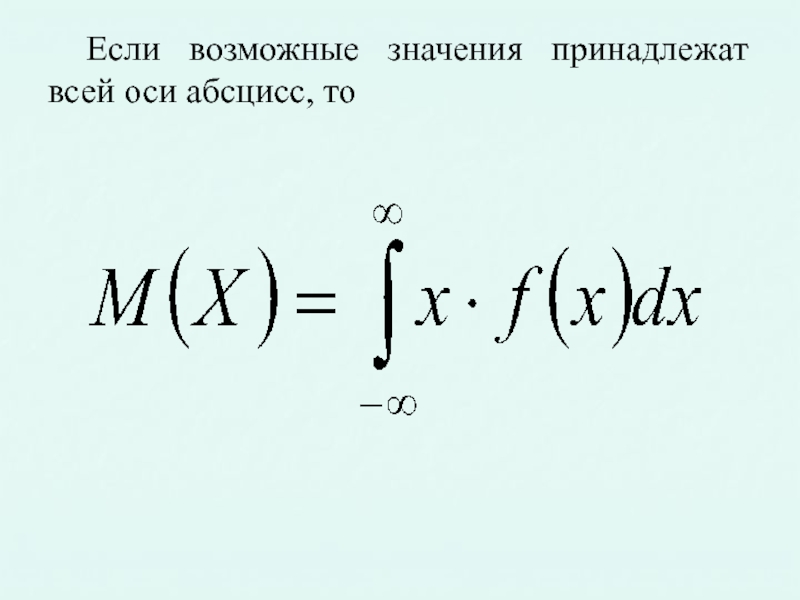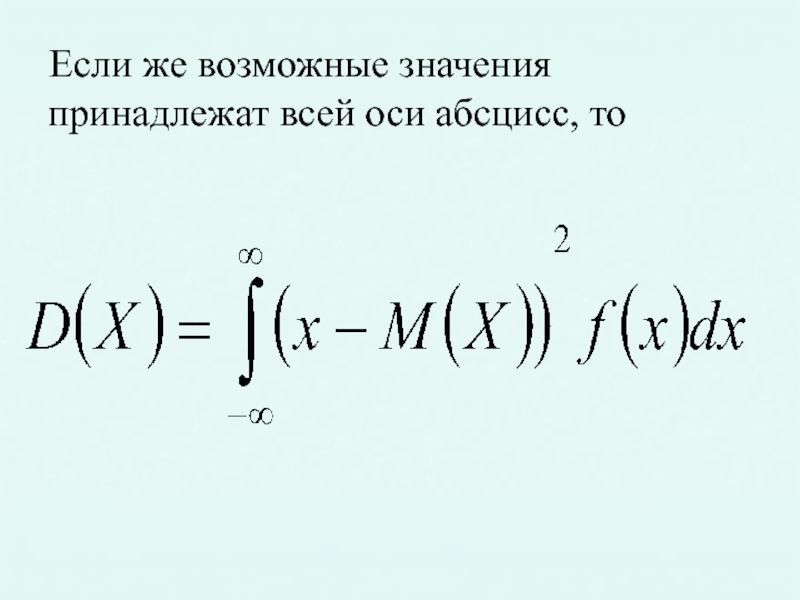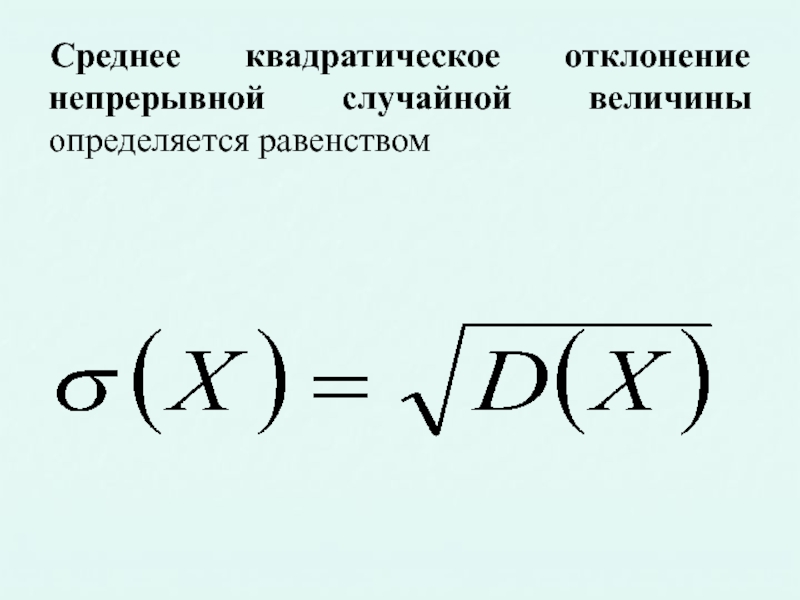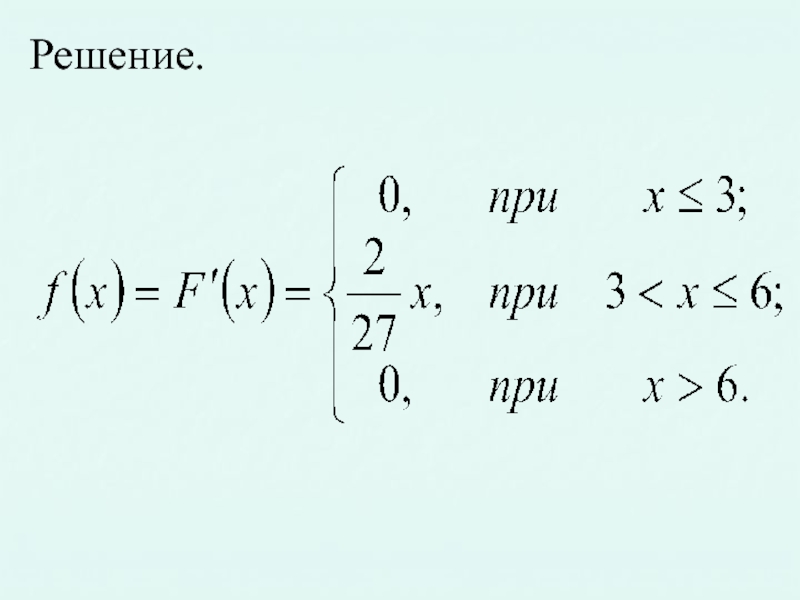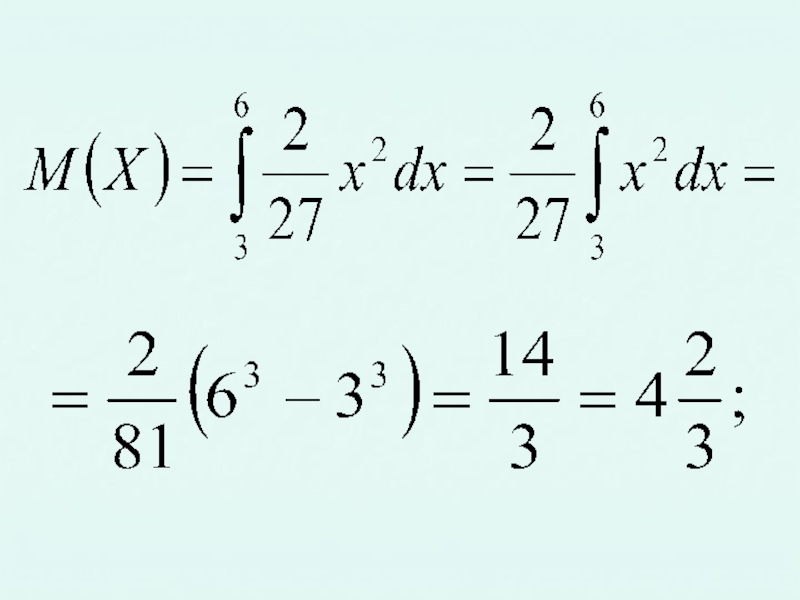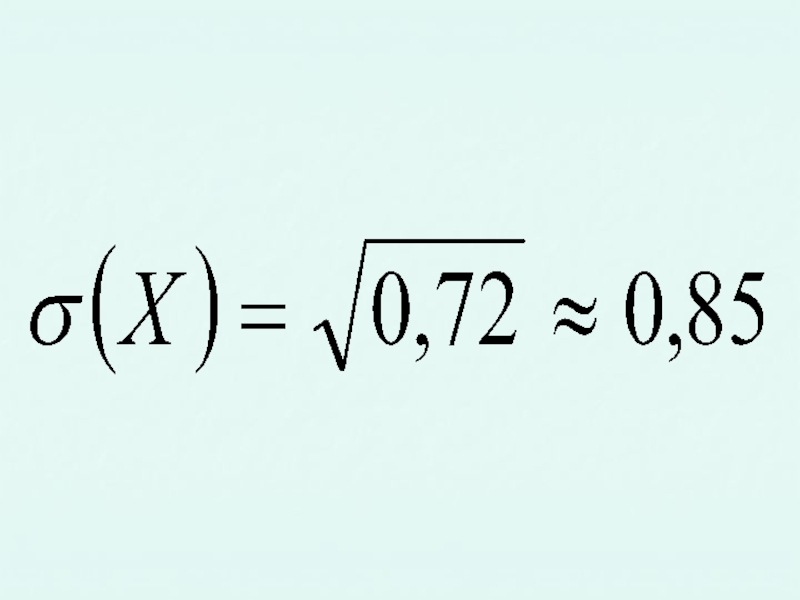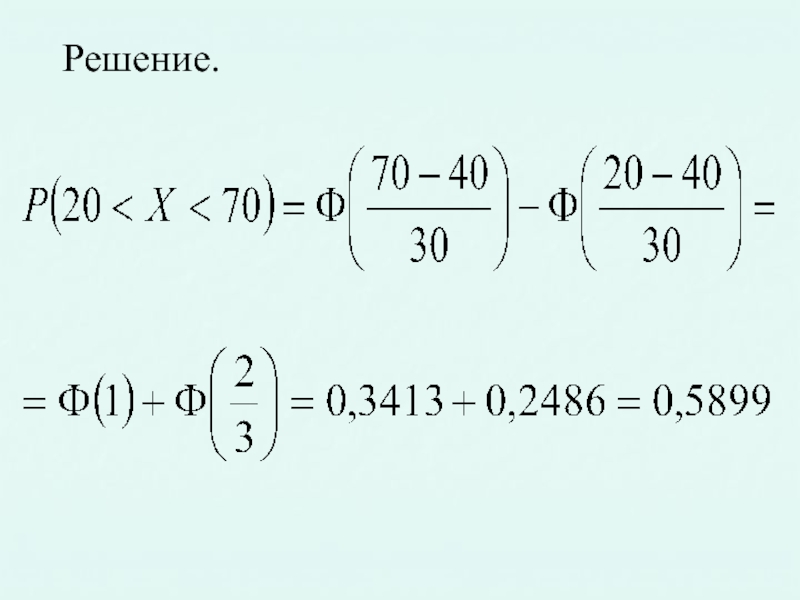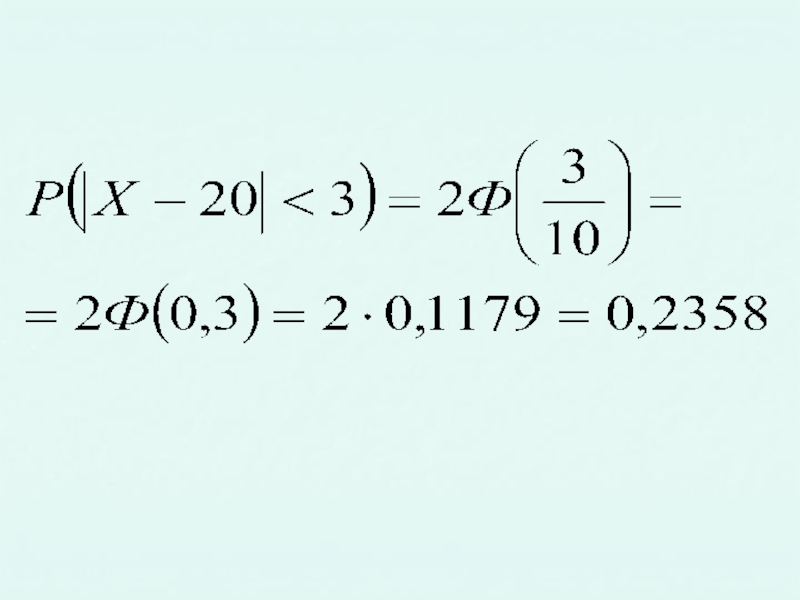- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Непрерывные случайные величины и их числовые характеристики презентация
Содержание
- 1. Непрерывные случайные величины и их числовые характеристики
- 2. План: 1. Плотность распределения и ее свойства. 2. Числовые характеристики НСВ.
- 3. 1. Плотность распределения и ее свойства
- 4. Ее также называют дифференциальной функцией распределения.
- 5. Теорема. Вероятность того, что непрерывная случайная величина
- 6. Свойства плотности распределения 1) Плотность распределения
- 7. 2. Числовые характеристики НСВ Математическим ожиданием непрерывной
- 8. Если возможные значения принадлежат всей оси абсцисс, то
- 9. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
- 10. Если возможные значения принадлежат отрезку , то
- 11. Если же возможные значения принадлежат всей оси абсцисс, то
- 12. Среднее квадратическое отклонение непрерывной случайной величины определяется равенством
- 13. Замечание 1. Свойства математического ожидания и
- 14. Замечание 2. Для вычисления дисперсии НСВ
- 15. Пример. Найти плотность распределения и числовые характеристики
- 16. Решение.
- 20. Тема. Основные законы распределения НСВ План:
- 21. При решении задач, которые выдвигает практика, приходится
- 22. Плотности распределений непрерывных случайных величин называют также
- 23. 1. Равномерный закон распределения Распределение вероятностей называют
- 24. НСВ считается равномерно распределенной, если ее плотность вероятности имеет вид
- 25. Числовые характеристики равномерно распределенной случайной величины находятся по следующим формулам:
- 26. Пример. Случайная величина распределена равномерно в интервале
- 27. 2. Показательный закон распределения Показательным (экспоненциальным) называют
- 28. Показательное распределение определяется одним параметром
- 29. Найдем функцию распределения показательного закона: Итак,
- 30. Функция распределения показательного закона имеет вид:
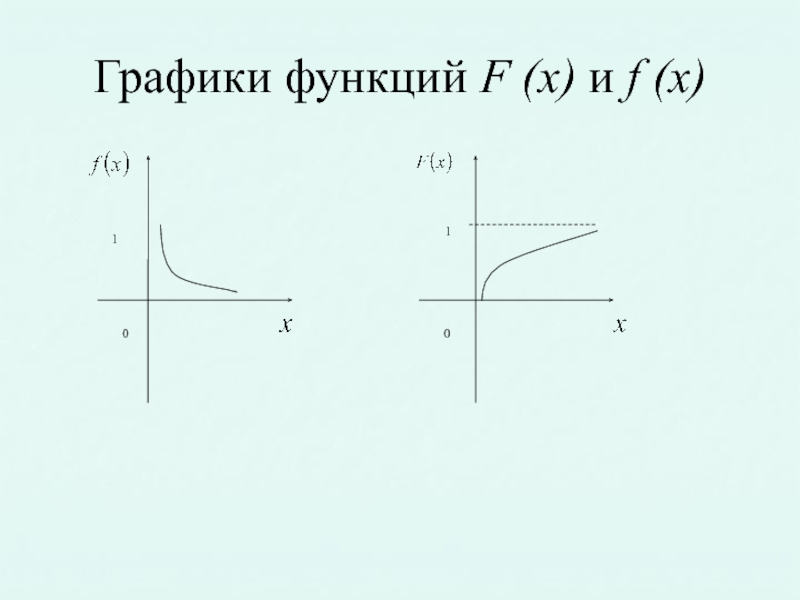
- 31. Графики функций F (x) и f (x) 0 1 0 1
- 32. Вероятность попадания в заданный интервал показательно распределенной
- 33. Пример. Непрерывная случайная величина X распределена
- 34. Числовые характеристики показательного распределения Числовые характеристики
- 35. Пример. Непрерывная случайная величина X распределена по
- 36. Пример. Непрерывная случайная величина X распределена по
- 37. 3. Нормальный закон распределения Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
- 38. Нормальное распределение определяется двумя параметрами:
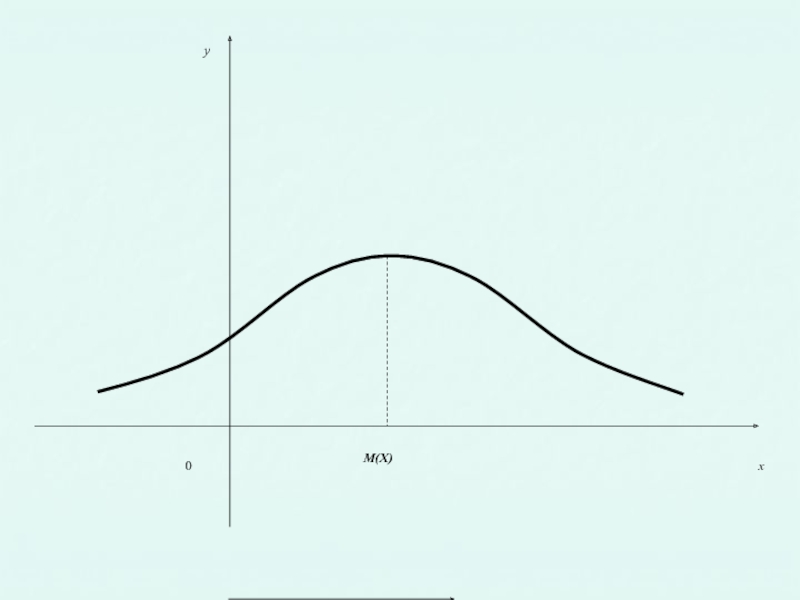
- 39. Нормальная кривая График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
- 40. 0 x y M(X)
- 41. Влияние параметров нормального распределения на форму нормальной
- 42. С возрастанием среднего квадратического отклонения максимальная ордината
- 43. При убывании среднего квадратического отклонения нормальная кривая
- 44. 0 x y M(X)
- 45. При математическом ожидании равном нулю и среднем
- 46. Вероятность попадания в заданный интервал нормальной случайной
- 47. Вероятность попадания в заданный интервал нормальной случайной
- 48. В результате преобразований и использования функции Лапласа
- 49. окончательно получим
- 50. Пример. Случайная величина X распределена по нормальному
- 51. Решение.
- 52. Вычисление вероятности заданного отклонения Часто требуется
- 54. Пример. Случайная величина распределена нормально
- 55. Решение. Используя формулу и
- 57. Правило трех сигм Правило трех сигм:
- 58. На практике правило трех сигм применяют так:
Слайд 31. Плотность распределения и ее свойства
Плотностью распределения вероятностей или плотностью
распределения f (x) непрерывной случайной величины X называется производная ее функции распределения F (x)
Слайд 5Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее
интервалу (a ; b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:
Слайд 6Свойства плотности распределения
1) Плотность распределения вероятностей неотрицательная функция
2) Площадь фигуры, ограниченной
кривой распределения и осью абсцисс, равна единице
Слайд 72. Числовые характеристики НСВ
Математическим ожиданием непрерывной случайной величины X, возможные значения
которой принадлежат отрезку от a до b, называют определенный интеграл:
Слайд 9Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Слайд 13Замечание 1.
Свойства математического ожидания и дисперсии дискретных случайных величин сохраняются
и для непрерывных величин.
Слайд 15Пример. Найти плотность распределения и числовые характеристики случайной величины X заданной
интегральной функцией распределения
Слайд 20Тема. Основные законы распределения НСВ
План:
Равномерный закон распределения.
Показательный закон распределения.
Нормальный закон
распределения.
Слайд 21При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями
непрерывных случайных величин.
Слайд 22Плотности распределений непрерывных случайных величин называют также законами распределений.
Часто встречаются
законы равномерного, нормального и показательного распределений.
Слайд 231. Равномерный закон распределения
Распределение вероятностей называют равномерным, если на интервале, которому
принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Слайд 25Числовые характеристики равномерно распределенной случайной величины находятся по следующим формулам:
Слайд 26Пример. Случайная величина распределена равномерно в интервале (2;8). Найти ее математическое
ожидание и дисперсию.
Решение.
Решение.
Слайд 272. Показательный закон распределения
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
X, которое описывается плотностью
где - постоянная положительная величина.
где - постоянная положительная величина.
Слайд 28
Показательное распределение определяется одним параметром .
Эта особенность
показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров.
Слайд 32Вероятность попадания в заданный интервал показательно распределенной случайной величины
Вероятность попадания
в интервал непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения
вычисляется по формуле
вычисляется по формуле
Слайд 33Пример. Непрерывная случайная величина X распределена по показательному закону
при ;
при .
Найти вероятность того, что в результате испытания X попадет в интервал (0,3 ;1).
Решение. По условию, .
при .
Найти вероятность того, что в результате испытания X попадет в интервал (0,3 ;1).
Решение. По условию, .
Слайд 34Числовые характеристики показательного распределения
Числовые характеристики непрерывной случайной величины X распределенной
по показательному закону вычисляются по формулам:
Слайд 35Пример. Непрерывная случайная величина X распределена по показательному закону
при ;
при .
Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.
при .
Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.
Слайд 36Пример. Непрерывная случайная величина X распределена по показательному закону
при ;
при .
Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.
Решение. По условию, . Следовательно,
при .
Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.
Решение. По условию, . Следовательно,
Слайд 373. Нормальный закон распределения
Нормальным называют распределение вероятностей непрерывной случайной величины, которое
описывается плотностью
Слайд 38Нормальное распределение определяется двумя параметрами:
Достаточно знать эти параметры, чтобы
задать нормальное распределение.
Слайд 39 Нормальная кривая
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
Слайд 41Влияние параметров нормального распределения на форму нормальной кривой.
Изменение величины параметра
не
изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси абсцисс: вправо, если математическое ожидание возрастает и влево, если оно убывает.
Слайд 42С возрастанием среднего квадратического отклонения максимальная ордината нормальной кривой убывает, а
сама кривая становится более пологой, т.е. сжимается к оси абсцисс.
Слайд 43При убывании среднего квадратического отклонения нормальная кривая становится более «островершинной» и
растягивается в положительном направлении оси ординат.
Слайд 45При математическом ожидании равном нулю и среднем квадратическом отклонении равном единице
нормальную кривую называют нормированной.
Слайд 46Вероятность попадания в заданный интервал нормальной случайной величины
Пусть случайная величина распределена
по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу , равна
Слайд 47Вероятность попадания в заданный интервал нормальной случайной величины
Пусть случайная величина распределена
по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу , равна
Слайд 50Пример. Случайная величина X распределена по нормальному закону с математическим ожиданием
равным 40 и средним квадратическим отклонением 30 . Найти вероятность того, что X примет значение, принадлежащее интервалу (20;70).
Слайд 52Вычисление вероятности заданного отклонения
Часто требуется вычислить вероятность того, что отклонение нормально
распределенной случайной величины по абсолютной величине меньше заданного положительного числа , т. е. найти вероятность осуществления неравенства
Слайд 54Пример. Случайная величина распределена нормально
Найти вероятность того, что отклонение по
абсолютной величине будет меньше трех.
Слайд 55Решение. Используя формулу
и данные условия задачи:
а также используя таблицу
значений функции Лапласа, получим:
Слайд 57 Правило трех сигм
Правило трех сигм: Если случайная величина имеет нормальный
закон распределения с параметрами
то практически достоверно (вероятность 0,9973), что ее значения заключены в интервале
то практически достоверно (вероятность 0,9973), что ее значения заключены в интервале
Слайд 58На практике правило трех сигм применяют так: если распределение изучаемой величины
неизвестно, но условие, указанное в правиле выполняется, то есть основание предполагать, что изучаемая величина распределена нормально.
