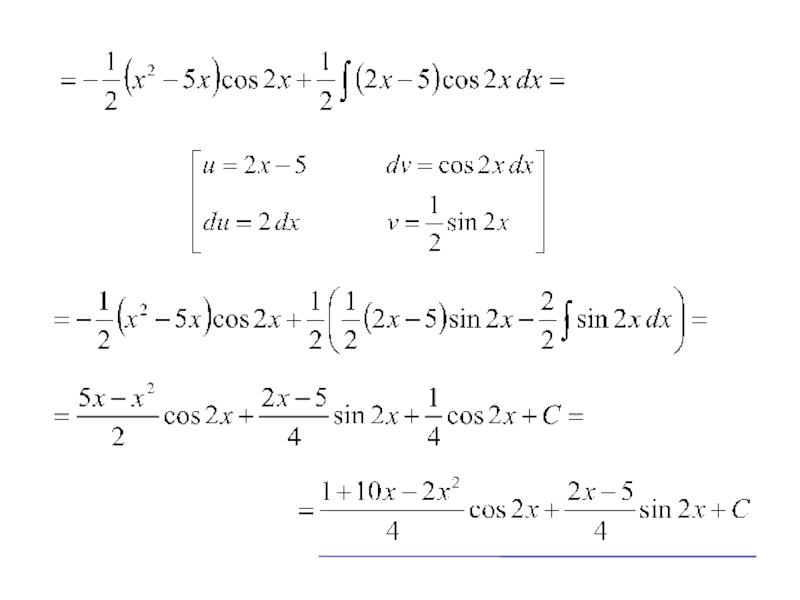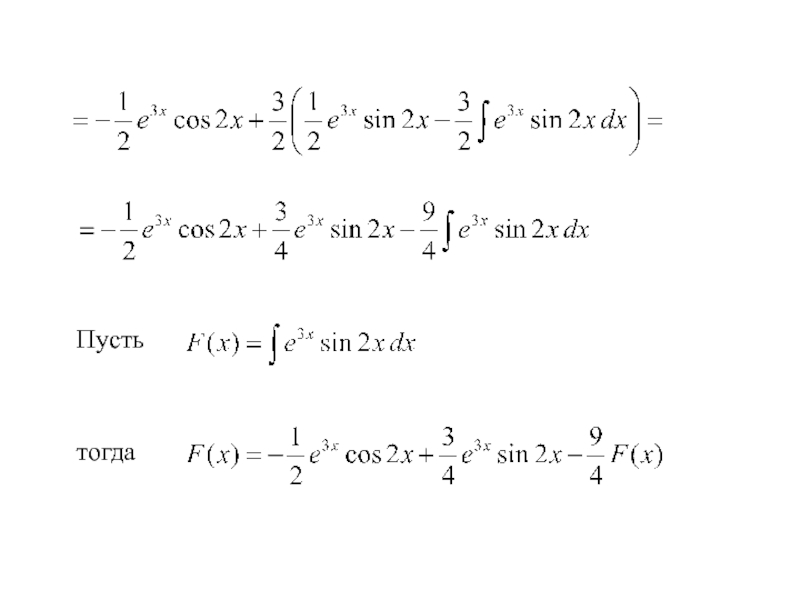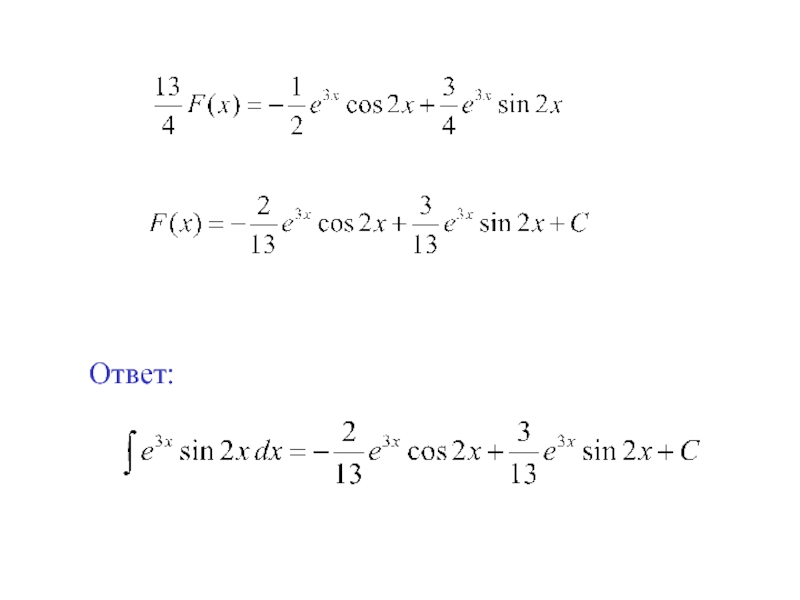- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределённый интеграл презентация
Содержание
- 1. Неопределённый интеграл
- 2. Вопросы лекции Свойства неопределенного интеграла Метод интегрирования по частям Интегрирование рациональных дробей Интегрирование тригонометрических функций
- 3. Свойства неопределенного интеграла Производная из неопределенного интеграла
- 4. Свойства неопределенного интеграла
- 5. Свойства неопределенного интеграла
- 6. Свойства неопределенного интеграла
- 7. Свойства неопределенного интеграла
- 8. Свойства неопределенного интеграла
- 9. Свойства неопределенного интеграла
- 10. Метод интегрирования по частям.
- 13. Некоторые типы
- 14. u=P(x) - многочлен Если Р(х) выше
- 18. Пример 4. Вычислить интеграл
- 19. Пусть тогда
- 20. Ответ:
- 21. Пример 5. Вычислить интеграл
- 22. Интегрирование рациональных дробей Всякую рациональную функцию можно
- 23. Интегрирование рациональных дробей Правильные рациональные дроби вида:
- 24. Интегрирование рациональных дробей
- 25. Интегрирование рациональных дробей
- 26. Интегрирование рациональных дробей
- 27. Интегрирование рациональных дробей
Вопросы лекции Свойства неопределенного интеграла Метод интегрирования по частям Интегрирование рациональных дробей Интегрирование тригонометрических функций
Слайд 2Вопросы лекции
Свойства неопределенного интеграла
Метод интегрирования по частям
Интегрирование рациональных дробей
Интегрирование тригонометрических функций
Слайд 3Свойства неопределенного интеграла
Производная из неопределенного интеграла равна подынтегральной функции, т.е. если
, то и
Слайд 11
то
Если интеграл, стоящий справа, проще интеграла, стоящего слева, то применение формулы
имеет смысл.
Слайд 13
Некоторые типы интегралов, решаемые методом интегрирования по частям.
где Р(х)- многочлен
u
u
u
u
u
Слайд 14
u=P(x) - многочлен
Если Р(х) выше первой степени, то операцию интегрирования по
частям следует применять несколько раз.
u
u
u
Формула применяется два раза, причем оба раза за u выбирается либо показательная функция, либо тригонометрическая.
Слайд 22Интегрирование рациональных дробей
Всякую рациональную функцию можно представить в виде рациональной дроби,
т.е. в виде отношения двух многочленов
