- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл презентация
Содержание
- 1. Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл
- 2. Основная литература 1. Шипачев В. С.
- 3. Отчетность Контрольная работа. Выполняется в соответствии: Задания
- 4. Неопределенный интеграл, его свойства и вычисление Первообразная и неопределенный интеграл
- 8. Свойства интеграла Производная неопределенного интеграла
- 9. Свойства интеграла 3. Неопределенный интеграл от
- 10. Свойства интеграла
- 11. Таблица неопределенных интегралов
- 12. Таблица неопределенных интегралов
- 13. Свойства дифференциалов При интегрировании удобно пользоваться свойствами:
- 14. Примеры
- 15. Примеры
- 16. Независимость от вида переменной
- 17. Пример Вычислим
- 18. Методы интегрирования Интегрирование по частям
- 19. Примеры
- 20. Примеры
- 21. Метод замены переменной
- 22. Интегрирование функций, содержащих квадратный трехчлен
- 23. Пример
- 24. Пример Найти
- 25. Определенный интеграл, его основные свойства. Формула Ньютона-
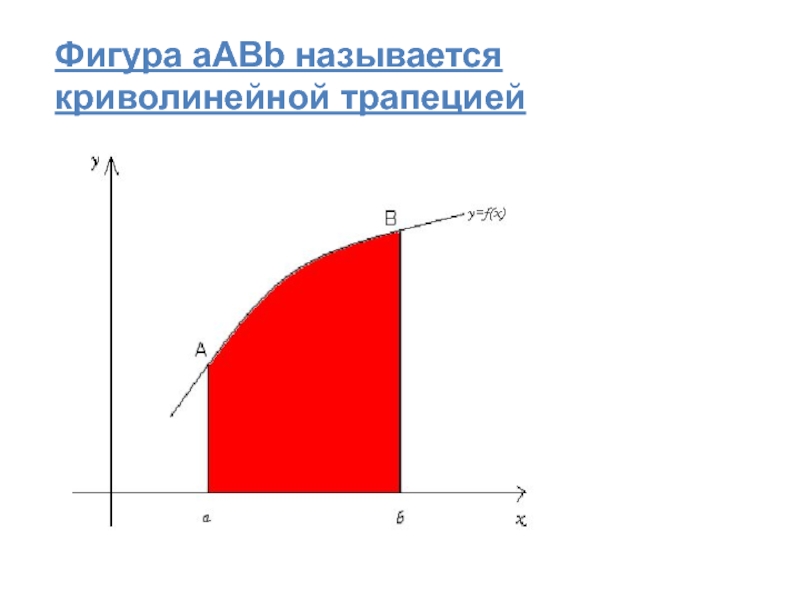
- 26. Фигура aABb называется криволинейной трапецией
- 27. Определение
- 28. Правило: Определенный интеграл равен разности значений первообразной
- 29. Основные свойства определенного интеграла. 1)Величина определенного интеграла
- 30. 3) При перестановке пределов интегрирования определенный интеграл меняет
- 31. 5)Постоянный множитель можно выносить за знак определенного
- 32. 3. Замена переменной в определенном интеграле. где
- 33. Несобственные интегралы. Определение. Пусть функция f(x) определена
- 34. Таким образом, по определению, Если
- 35. Пример. Интеграл Пуассона: если
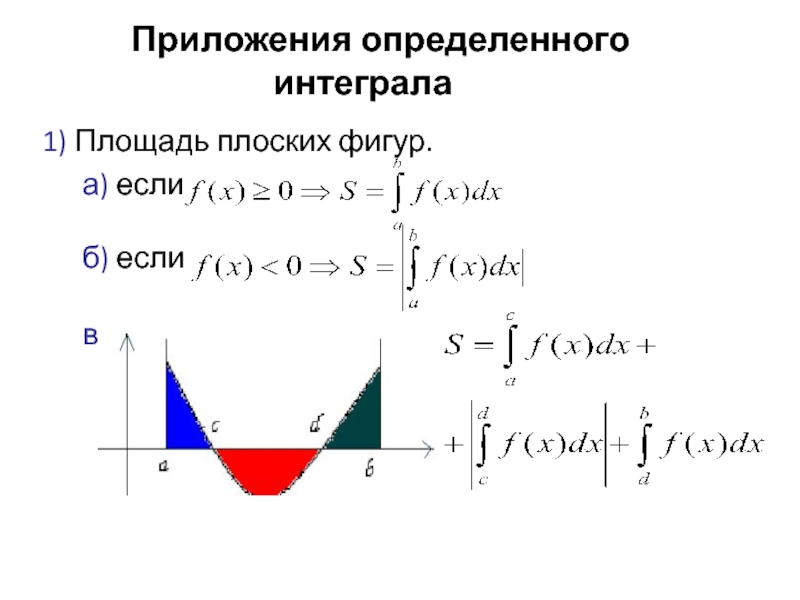
- 36. 5. Приложения определенного интеграла 1) Площадь плоских фигур.
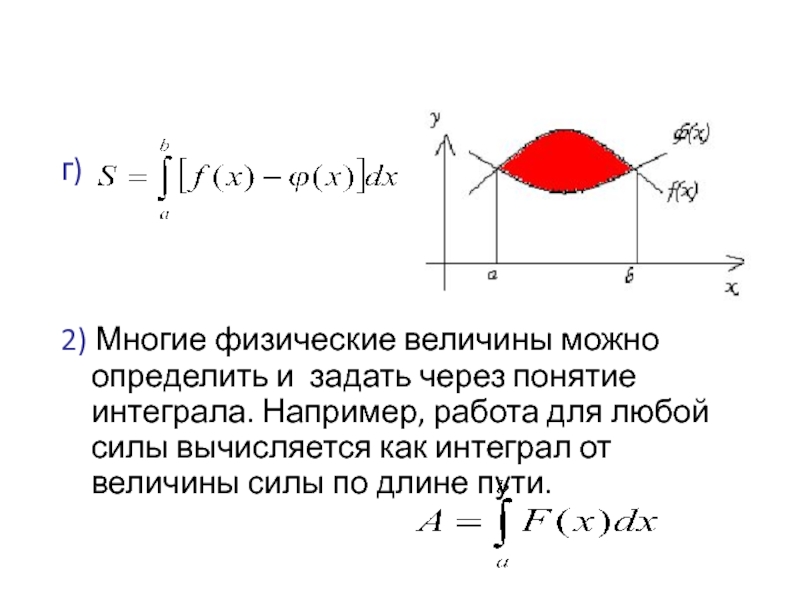
- 37. г) 2) Многие физические
- 38. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
- 39. Частные приращения и частные производные
- 40. Полное приращение функции 2-х переменных
- 41. Полное приращение и полный дифференциал
- 42. Дифференциалы высшего порядка Дифференциалом второго
- 43. Экстремумы функции двух переменных Определение.
- 44. Экстремумы функции двух переменных
- 45. Достаточные условия экстремума функции двух переменных
- 46. Пример Исследовать на экстремум функцию
- 47. Наибольшее и наименьшее значения функции
- 48. Известно, что непрерывная
- 49. Пусть функция непрерывна в замкнутой
- 50. Скалярное поле Основные определения
- 51. Скалярное поле Основные определения
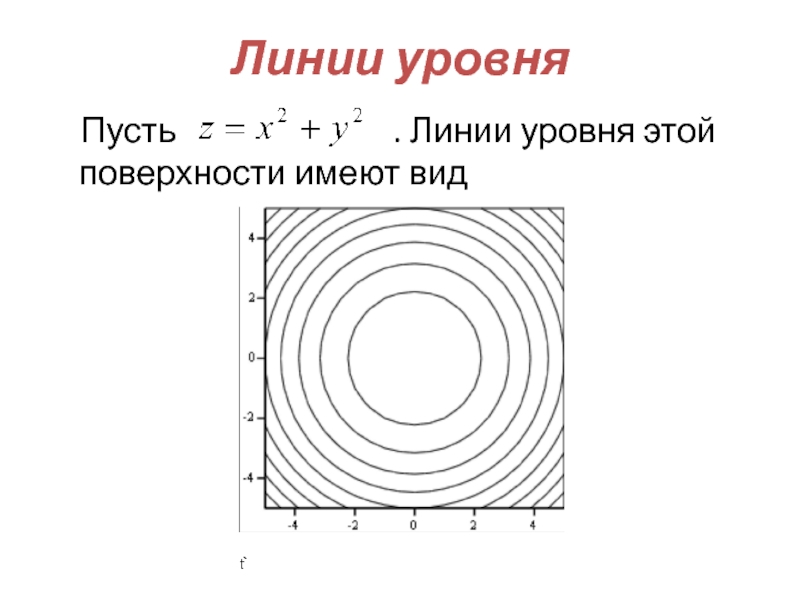
- 52. Если область D расположена на
- 53. Пусть
- 54. Линии уровня Пусть
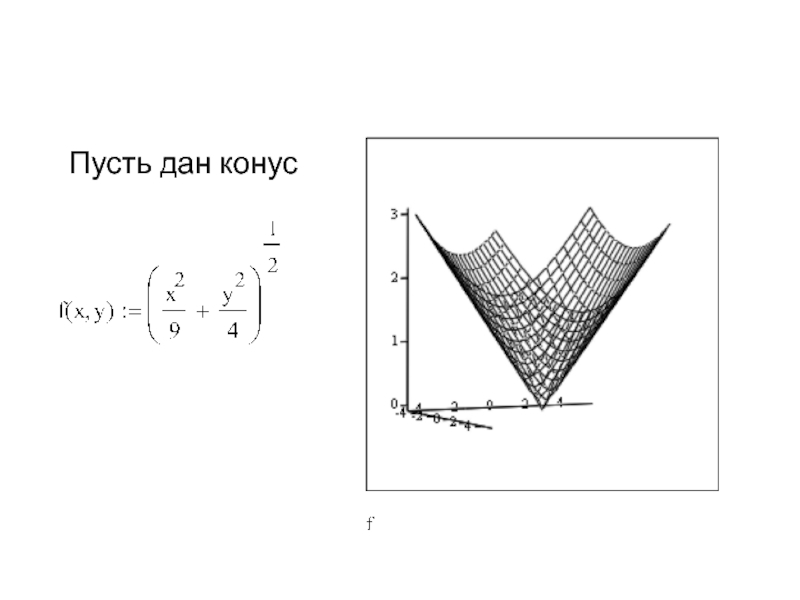
- 55. Пусть дан конус
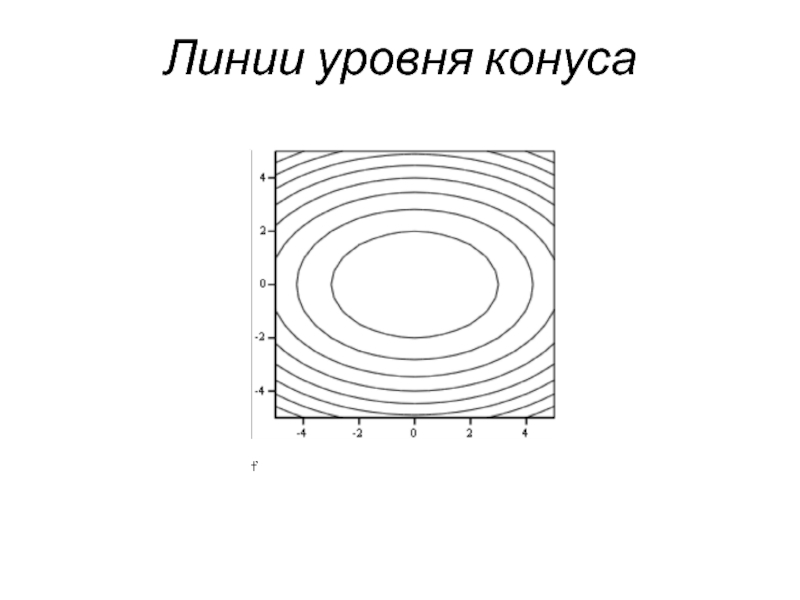
- 56. Линии уровня конуса
- 57. Пусть задана дифференцируемая функция
- 58. Определение Пусть
- 59. Производной функции
- 60. Вычисление производной по направлению Формула вычисления производной по направлению:
- 61. Градиент скалярного поля Градиентом скалярного
- 62. Пример Найти
- 63. Направление градиента Теорема. Производная функции
- 64. Направление градиента Так как производная
- 65. Величина градиента плоского скалярного поля
- 66. Градиент скалярного поля
- 67. Обыкновенные дифференциальные уравнения Обыкновенным дифференциальным уравнением называется
- 68. ОДУ первого порядка Обыкновенным дифференциальным уравнением
- 69. Разделяют несколько типов (видов) обыкновенных дифференциальных уравнений:
- 70. Уравнения с разделёнными переменными. Так
- 71. Уравнения с разделяющимися переменными. Так
- 72. Выразим у из последнего выражения как функцию х, получим общее решение: Пример:
- 73. Уравнения с однородной правой частью. Так называются
- 74. Пример:
- 75. Окончательно, получим общее решение: Пример:
- 76. Линейные уравнения. ДУ первого порядка называется линейным,
- 77. Для решения уравнения представим y(x) в виде
- 78. Отметим, решая уравнение на v(x) мы не
- 79. Пример:
- 80. Для нахождения частного решения, соответствующего начальным условиям
- 81. Уравнение в полных дифференциалах. Так называется уравнение
- 82. Для нахождения функции u(x, y) решается система
- 83. Пример: найти общее решение уравнения Убедимся,
- 84. ОДУ высших порядков
- 85. Некоторые типы уравнений, допускающие понижение порядка.
- 86. Уравнение, не содержащее в явном виде неизвестную
- 87. Пример: Понизить порядок уравнения:
- 88. Уравнение, не содержащее в явном виде независимую
- 89. Спасибо за внимание!
Слайд 2Основная литература
1. Шипачев В. С. Высшая математика. Базовый курс: учебник и
2. Шипачев В. С. Высшая математика. Полный курс: учебник для акад. бакалавриата [Гриф УМО] / В. С. Шипачев; под ред. А. Н. Тихонова. - 4-е изд., испр. и доп. - Москва : Юрайт, 2015. - 608 с
3. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика в упражнениях и задачах. [Текст] / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. В 2 ч. – М.: Высшая школа, 2007. – 304+415c.
Слайд 3Отчетность
Контрольная работа. Выполняется в соответствии:
Задания и методические указания к выполнению контрольных
Вариант контрольной работы выбирать по последней цифре номера зачетной книжки.
2. Экзамен
Слайд 8Свойства интеграла
Производная неопределенного интеграла равна подынтегральной функции, а его
Слайд 9Свойства интеграла
3. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен
так как является первообразной для
Слайд 25Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного интеграла.
К понятию определенного интеграла приводит задача нахождения площади криволинейной трапеции.
Пусть на некотором интервале [a,b] задана непрерывная функция
Задача:
Построить ее график и найти F площадь фигуры, ограниченной этой кривой, двумя прямыми x = a и x = b, а снизу – отрезком оси абсцисс между точками x = a и x = b.
Слайд 27
Определение
Под определенным интегралом
от данной непрерывной функции f(x) на данном отрезке [a;b] понимается соответствующее приращение ее первообразной, то есть
Числа a и b – пределы интегрирования, [a;b] – промежуток интегрирования.
Слайд 28Правило:
Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и
Введя обозначения для разности
Формула Ньютона – Лейбница.
Слайд 29Основные свойства определенного интеграла.
1)Величина определенного интеграла не зависит от обозначения переменной
где x и t – любые буквы.
2)Определенный интеграл с одинаковыми пределами интегрирования равен нулю
Слайд 303) При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный
(свойство
4) Если промежуток [a;b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутку [a;b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
Слайд 315)Постоянный множитель можно выносить за знак определенного интеграла.
6)Определенный интеграл от алгебраической
Слайд 323. Замена переменной в определенном интеграле.
где
для
Пример: =
=
Слайд 33 Несобственные интегралы.
Определение. Пусть функция f(x) определена на бесконечном интервале [a; +
,
то этот предел называется несобственным интегралом функции f(x) на интервале
[a; + ∞) и обозначается .
Слайд 34Таким образом, по определению,
Если этот предел - некоторое число, то
интеграл
называется
Слайд 37г)
2) Многие физические величины можно определить и задать через понятие интеграла.
Слайд 38ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Если каждой паре (x,y) значений
Слайд 40Полное приращение функции 2-х переменных
Если обеим переменным дать приращение,
Слайд 42Дифференциалы высшего порядка
Дифференциалом второго порядка функции z=f(x,y) называется
Если х и у независимые переменные, то .
Слайд 43Экстремумы функции двух переменных
Определение. Говорят, что в точке
Аналогично определяется минимум функции.
Минимум и максимум функции называются ее экстремумами.
.
Слайд 44Экстремумы функции двух переменных
Теорема (необходимое условие экстремума).
Точки, в которых выполнены эти условия, называются критическими.
Слайд 45Достаточные условия экстремума функции двух переменных
Теорема. Пусть функция
, в которой . Если при этом в этой точке выполнено условие , то точка является точкой экстремума функции, причем точкой максимума, если
, и точкой минимума, если .
Если же в этой точке , то экстремума в точке
нет.
В том случае, если в точке , теорема ответа не дает.
Слайд 47Наибольшее и наименьшее значения функции
Определение. Наименьшее или наибольшее значение
Слайд 48 Известно, что непрерывная в замкнутой ограниченной области
Абсолютный экстремум достигается функцией либо в критических точках, либо на границе области.
Слайд 49 Пусть функция непрерывна в замкнутой ограниченной области G, дифференцируема
1)найти критические точки, принадлежащие этой области, и вычислить в них значения функции;
2)найти наибольшее и наименьшее значения функции на границе области;
3)из всех найденных значений выбрать наибольшее и наименьшее.
Слайд 50Скалярное поле
Основные определения
Пусть в
Слайд 51Скалярное поле
Основные определения
Множество точек М области D,
Слайд 52 Если область D расположена на плоскости Оху, то поле
Поверхности уровня называют в этом случае линиями уровня.
Слайд 57 Пусть задана дифференцируемая функция
Рассмотрим точку этого поля и луч
, выходящий из точки P в направлении единичного вектора
где –углы, образованные вектором
с осями координат .
Слайд 58Определение
Пусть
– расстояние между точками P и ; называют величиной перемещения. Приращением функции в направлении назовем разность
Слайд 59 Производной функции
в точке P по направлению
к величине перемещения при :
.
Слайд 61Градиент скалярного поля
Градиентом скалярного поля u=u(x,y,z), где u=u(x,y,z)-дифференцируемая функция,
.
Таким образом,
или .
Слайд 62Пример
Найти градиент функции u=
Решение. Вычислим градиент функции.
Тогда grad u = + +
А в точке М
Слайд 63Направление градиента
Теорема. Производная функции по направлению
Слайд 64Направление градиента
Так как производная по направлению представляет
градиент функции в данной точке указывает направление наиболее быстрого возрастания функции.
Слайд 65Величина градиента плоского скалярного поля
Величина градиента плоского скалярного поля
| grad u | =
обозначается tgϕ и определяет крутизну наибольшего ската или подъема поверхности u = f (x, y).
Слайд 66
Градиент скалярного поля в данной точке по величине
,
где .
Слайд 67Обыкновенные дифференциальные уравнения
Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения
Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
Пример: y(4) – y + x = 0 - уравнение четвёртого порядка.
Функция y(x) называется решением (или интегралом) дифференциального уравнения если при подстановке ее в уравнение обращает его в тождество.
Слайд 68ОДУ первого порядка
Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида:
где
Общее решение:
Пример: общее решение:
Слайд 69Разделяют несколько типов (видов) обыкновенных дифференциальных уравнений:
-Уравнения с разделяющимися переменными,
-Однородные уравнения,
-Линейные
-Уравнение в полных дифференциалах,
-и т.д.
Остановимся подробнее на каждом из этих типов уравнений.
Слайд 70Уравнения с разделёнными переменными.
Так называются уравнения вида удовлетворяющее начальному условию
f(x)dx + g(y)dy = 0,
Интегрируя, получим
- общий интеграл (общее решение) этого уравнения.
Пример:
- общее решение
Слайд 71Уравнения с разделяющимися переменными.
Так называются уравнения вида
Эти уравнения легко
переменными:
Записываем уравнение в форме:
затем делим на g(y) и умножаем на dx: .
Это уравнение - с разделёнными переменными. Интегрируя, получим общий интеграл:
Слайд 73Уравнения с однородной правой частью. Так называются уравнения со специальным видом
Это уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u(x) заменой:
Подставляя в уравнение y = x·u, y ′ = u + x·u ′, получим
(это - уравнение с разделяющимися переменными),
- это общий интеграл уравнения относительно переменных x, u
Слайд 76Линейные уравнения. ДУ первого порядка называется линейным, если неизвестная функция y(x)
здесь p(x), q(x) - непрерывные функции.
Пример:
Слайд 77Для решения уравнения представим y(x) в виде произведения двух новых неизвестных
Тогда
и уравнение приводится к виду:
или
Это уравнение решаем в два этапа: сначала находим функцию v(x) как частное решение уравнения с разделяющимися переменными:
затем находим u(x) из уравнения:
Слайд 78Отметим, решая уравнение на v(x) мы не вводим в это решение
Слайд 80Для нахождения частного решения, соответствующего начальным условиям (задача Коши), подставим в
Решение задачи:
Слайд 81Уравнение в полных дифференциалах. Так называется уравнение вида
(P(x, y), Q(x,
Необходимым и достаточным условием существования такой функции является условие:
Если - уравнение в полных дифференциалах, то его правая часть равна 0, т.е. принимает вид du(x, y) = 0. На решении y(x) получим du(x, y(x)) = 0, следовательно, u(x,y(x)) = C, где C - произвольная постоянная. Соотношение u(x, y) = C и есть общее решение уравнения в полных дифференциалах.
P(x, y) dx + Q(x, y) dy = 0.
Слайд 82Для нахождения функции u(x, y) решается система уравнений
Из первого уравнения этой
с точностью до произвольной дифференцируемой по y функции (эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x.
Дифференцируем эту функцию по y и приравниваем выражению, стоящему во втором уравнении системы (т.е. ), получим дифференциальное уравнение из которого можно найти .
Слайд 83Пример: найти общее решение уравнения
Убедимся, что это - уравнение в
.
Слайд 84ОДУ высших порядков
Обыкновенным дифференциальным уравнением называется уравнение,
Общим решением (общим интегралом) уравнения называется соотношение вида:
Слайд 85Некоторые типы уравнений, допускающие понижение порядка.
Уравнение вида
решается последовательным n-кратным
Переобозначив постояные, общее решение запишем в виде :
y = cos x + C1x3 + C2x2 + C3x + C4.
Пример:
Слайд 86Уравнение, не содержащее в явном виде неизвестную функцию и её младшие
Порядок уравнения вида F(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего функции y(x) и (k – 1) младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции
z(x) = y(k)(x). Тогда уравнение примет вид
т.е. будет уравнением (n – k)-го порядка.
После нахождения z(x) последовательным интегрированием решается
уравнение y(k)(x)= z(x).
Слайд 87Пример: Понизить порядок уравнения:
Младшая производная, входящая в явной
Тогда:
и уравнение примет вид
Слайд 88Уравнение, не содержащее в явном виде независимую переменную x.
Порядок уравнения
не
Пример: Понизить порядок уравнения:
Переменная x явно в уравнение не входит, поэтому полагаем ,
тогда .
Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений
поэтому рассматриваем два случая:




























![3) При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный (свойство аддитивности)4) Если промежуток [a;b]](/img/tmb/5/449777/c5aaef90aa3bc35e149d87e9eefd5e79-800x.jpg)