УГАТУ-2015
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нелинейные системы автоматического управления презентация
Содержание
- 1. Нелинейные системы автоматического управления
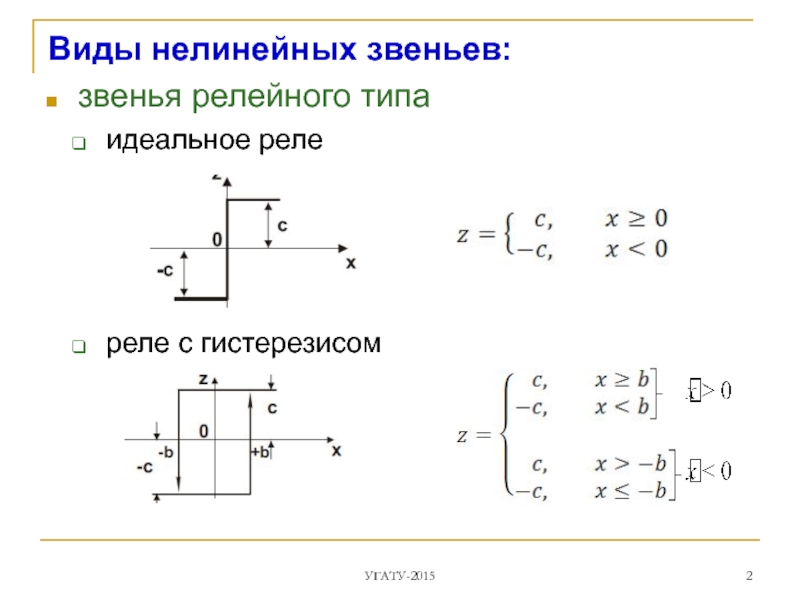
- 2. Виды нелинейных звеньев: звенья релейного типа идеальное
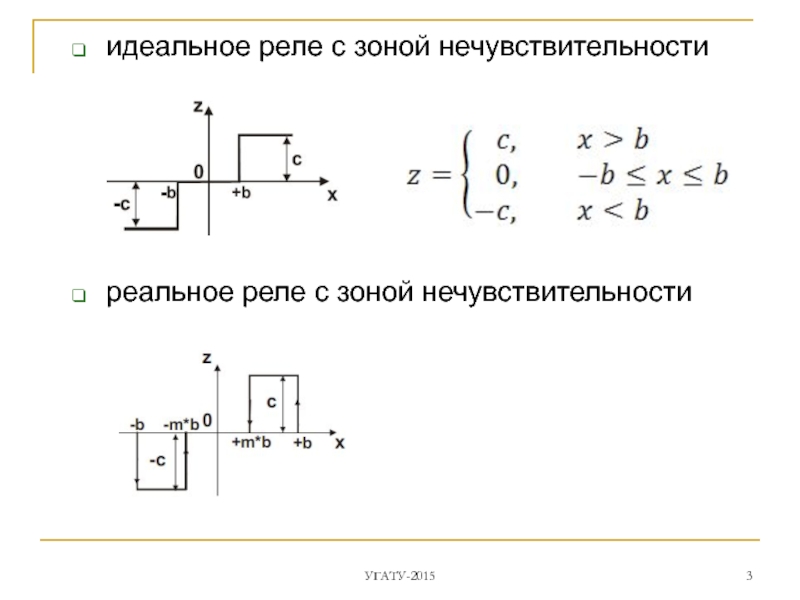
- 3. идеальное реле с зоной нечувствительности
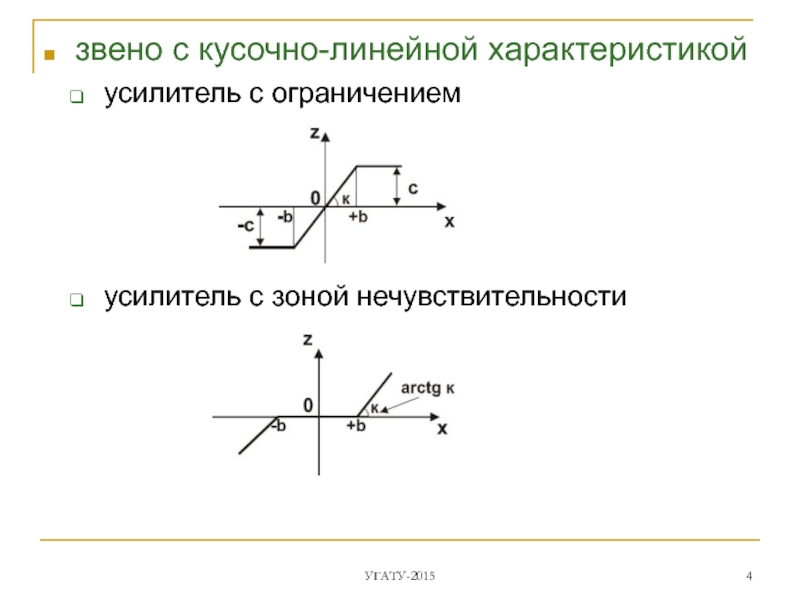
- 4. звено с кусочно-линейной характеристикой усилитель с ограничением
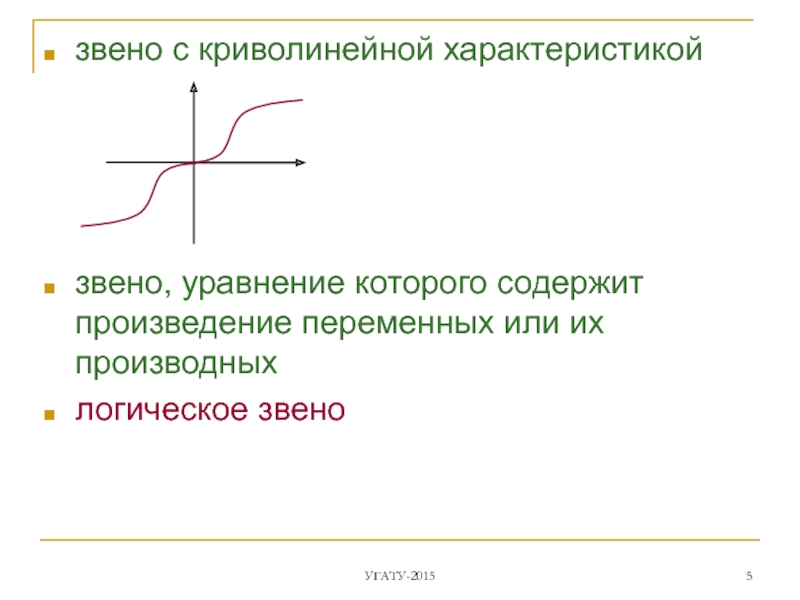
- 5. звено с криволинейной характеристикой
- 6. Метод гармонической линеаризации относится к приближенным
- 7. Идея метода гармонической линеаризации. Условия применимости
- 8. предполагается, что сигнал y(t), пройдя через
- 9. УГАТУ-2015
- 10. УГАТУ-2015
- 11. Решаются две группы задач: исследование периодических движений
- 12. Гармоническая линеаризация нелинейностей Пусть заданная нелинейная функция
- 13. Предполагаем где p=d/dt
- 14. Для однозначной нелинейной характеристики F(x) коэффициент q'(a)=0. Для неоднозначной характеристики типа гистерезис q'(a)≠0 и q'(a)
- 15. Замена исходного нелинейного уравнения приближенным уравнением для
- 16. Исследование устойчивости периодических движений методом гармонической линеаризации
- 17. Характеристическое уравнение гармонически линеаризованной нелинейной САУ:
- 18. определяются параметры ПД aп и ωп. УГАТУ-2015
- 19. Если при положительном приращении амплитуды ∆a>0 кривая
- 20. Частотный метод исследования устойчивости ПД в НС
- 21. s=jω решим полученное уравнение относительно неизвестных aп
- 22. УГАТУ-2015 q q’
- 23. УГАТУ-2015
- 24. Оба годографа и строятся на одной комплексной
- 25. УГАТУ-2015
- 26. УГАТУ-2015
- 27. Критерий абсолютной устойчивости В. М. Попова
- 28. линейная часть системы устойчива Абсолютная устойчивость
- 29. Теорема. Если замкнутая система состоит из устойчивой
- 30. Геометрическая интерпретация теоремы. введем видоизмененную частотную характеристику
- 31. (4) определяет собой прямую линию на плоскости
- 32. УГАТУ-2015
- 33. Второй метод Ляпунова не требует нахождения решения
- 34. исследуется изменение «расстояния» в пространстве состояний от
- 35. Суть второго метода Ляпунова сводится к оценке
- 36. УГАТУ-2015 а б Рис. 1. Изменение
- 37. УГАТУ-2015 Полной производной функции Ляпунова в силу
- 38. Теоремы второго метода Ляпунова Состояние равновесия системы
- 39. Теорема о неустойчивости Состояние равновесия системы
- 40. Пример с помощью второго метода Ляпунова
- 41. Выберем для нее в качестве функции Ляпунова
- 42. полная производная
Виды нелинейных звеньев: звенья релейного типа идеальное реле реле с гистерезисом УГАТУ-2015
Слайд 1Нелинейные системы автоматического управления
Нелинейной системой автоматического управления называется такая система, которая
содержит хотя бы одно звено описываемое нелинейным уравнением
Слайд 4звено с кусочно-линейной характеристикой
усилитель с ограничением
усилитель с зоной нечувствительности
УГАТУ-2015
Слайд 5звено с криволинейной характеристикой
звено, уравнение которого содержит произведение переменных или их
производных
логическое звено
логическое звено
УГАТУ-2015
Слайд 6Метод гармонической линеаризации
относится к приближенным методам
прост и универсален
широко распространен в
инженерной практике
УГАТУ-2015
Слайд 7Идея метода гармонической линеаризации. Условия применимости
Предполагается
в системе автоколебания с амплитудой ak
и частотой ωk.
Сигнал на входе НЗ
Сигнал на выходе НЗ
Сигнал на входе НЗ
Сигнал на выходе НЗ
УГАТУ-2015
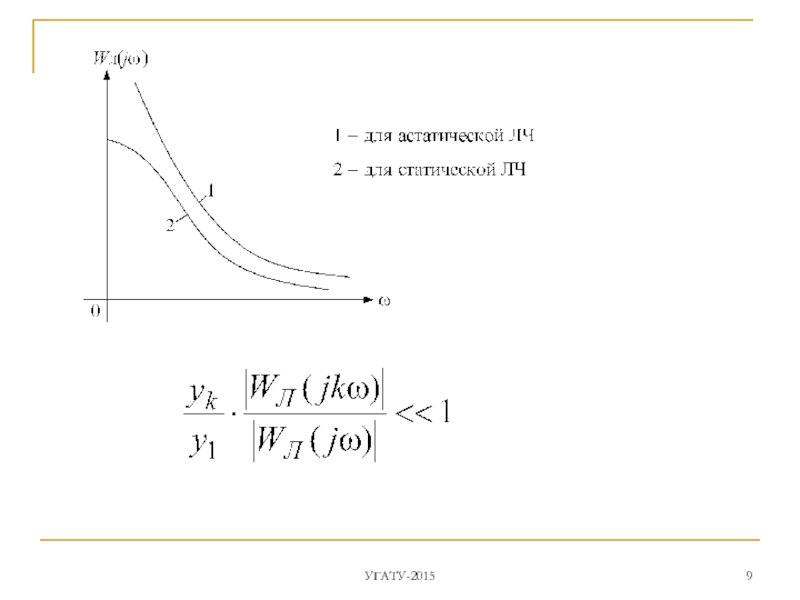
Слайд 8предполагается,
что сигнал y(t), пройдя через линейную часть WЛ(jω), фильтруется ею
в такой степени, что в сигнале на x(t) на выходе линейной части можно пренебречь высшими гармониками x2(t), x3(t)…и считать, что
Это предположение называется гипотезой фильтра.
Это предположение называется гипотезой фильтра.
УГАТУ-2015
Слайд 10УГАТУ-2015
- уравнение баланса амплитуд
- уравнение баланса фаз
гармонических колебаний
уравнения гармонического баланса
гармонических колебаний
уравнения гармонического баланса
(1)
(2)
(3)
Слайд 11Решаются две группы задач:
исследование периодических движений в нелинейных замкнутых системах (определение
условий устойчивости и параметров ПД);
исследование условий отсутствия моногармонических автоколебаний в нелинейных замкнутых системах.
исследование условий отсутствия моногармонических автоколебаний в нелинейных замкнутых системах.
УГАТУ-2015
Слайд 12Гармоническая линеаризация нелинейностей
Пусть заданная нелинейная функция
При выполнении гипотезы фильтра переменная x(t)
= a⋅sinωt = sinψ.
Разложим периодический сигнал на выходе НЗ в ряд Фурье:
Разложим периодический сигнал на выходе НЗ в ряд Фурье:
УГАТУ-2015
Слайд 14Для однозначной нелинейной характеристики F(x) коэффициент q'(a)=0.
Для неоднозначной характеристики типа
гистерезис q'(a)≠0 и q'(a)<0
УГАТУ-2015
Слайд 15Замена исходного нелинейного уравнения приближенным уравнением для первой гармоники называется гармонической
линеаризацией
передаточной функцией нелинейного гармонически линеаризованного звена
передаточной функцией нелинейного гармонически линеаризованного звена
УГАТУ-2015
Слайд 16Исследование устойчивости периодических движений методом гармонической линеаризации
Запишем уравнение замкнутой гармонически линеаризованной
нелинейной САУ в операторной форме:
- передаточная функция линейной
части, n[R(s)] ≤ m[Q(s)]
- передаточная функция линейной
части, n[R(s)] ≤ m[Q(s)]
УГАТУ-2015
Слайд 17Характеристическое уравнение гармонически линеаризованной нелинейной САУ:
подставим в L(s) s=jωп
выделим вещественную U(aп,ωп,)
и мнимую V(aп,ωп) части.
по критерию Михайлова
по критерию Михайлова
УГАТУ-2015
Слайд 19Если при положительном приращении амплитуды ∆a>0 кривая Михайлова займет положение 1-1,
а при отрицательном приращении амплитуды ∆a<0 займет положение 2-2, то исследуемые ПД с параметрами (aп,ωп) устойчивы, т.е. в НС имеют место автоколебания. В противном случае ПД – неустойчивы, а сама нелинейная САУ устойчива в малом.
УГАТУ-2015
Слайд 20Частотный метод исследования устойчивости ПД в НС Л. С. Голдфарба (1946 г.)
Основная идея
WН(a) − комплексный коэффициент передачи НЭ
УГАТУ-2015
(4)
Слайд 21s=jω
решим полученное уравнение относительно неизвестных aп и ωп .
Графоаналитическое решение
- инверсный коэффициент гармонической линеаризации
УГАТУ-2015
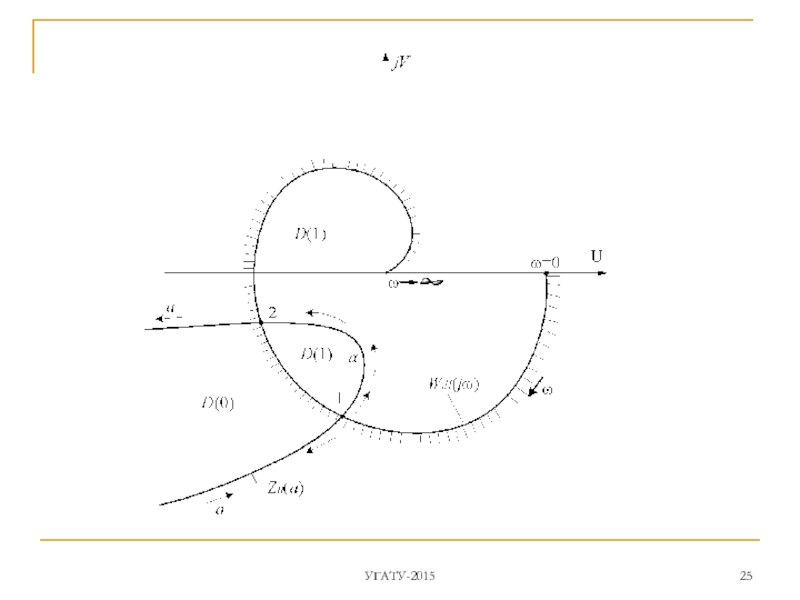
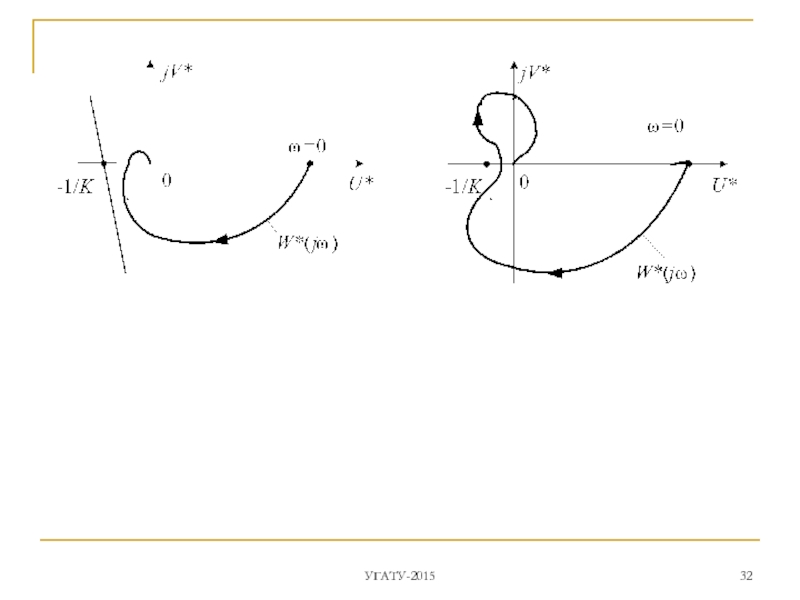
Слайд 24Оба годографа и строятся на одной комплексной плоскости.
- АФХ линейной части определяет частоту ωп ПД,
- амплитуду aп ПД.
ПД – устойчивы, если, двигаясь по характеристике в сторону возрастания амплитуды, переходим из неустойчивой в устойчивую область D-разбиения при устойчивой линейной части .
- амплитуду aп ПД.
ПД – устойчивы, если, двигаясь по характеристике в сторону возрастания амплитуды, переходим из неустойчивой в устойчивую область D-разбиения при устойчивой линейной части .
УГАТУ-2015
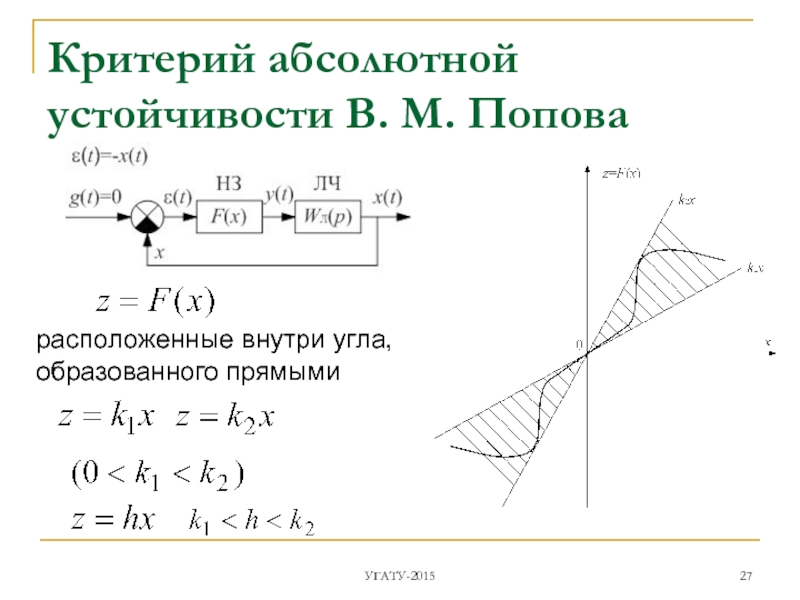
Слайд 27Критерий абсолютной устойчивости В. М. Попова
УГАТУ-2015
расположенные внутри угла, образованного прямыми
Слайд 28линейная часть системы устойчива
Абсолютная устойчивость нелинейной САУ предложена в 1959 г.
в работе румынского математика В. М. Попова.
УГАТУ-2015
Слайд 29Теорема. Если замкнутая система состоит из устойчивой линейной части с передаточной
функцией, все полюсы которой располагаются в левой полуплоскости, и нелинейного элемента с характеристикой , лежащей в угле
, то достаточным условием этой системы является выполнение при всех
неравенства
(1)
где q – произвольное вещественное число
, то достаточным условием этой системы является выполнение при всех
неравенства
(1)
где q – произвольное вещественное число
УГАТУ-2015
Слайд 30Геометрическая интерпретация теоремы.
введем видоизмененную частотную характеристику
обозначим
(2)
(3)
(4)
УГАТУ-2015
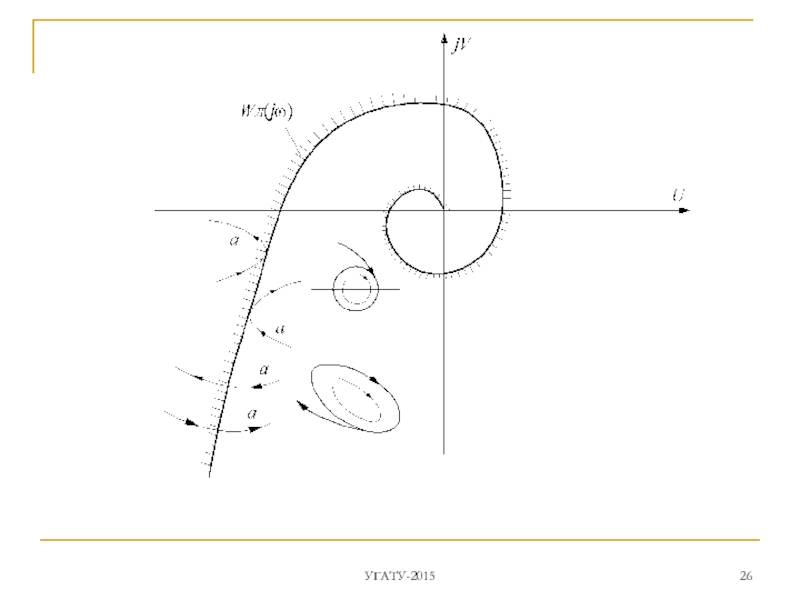
Слайд 31(4) определяет собой прямую линию на плоскости
, которая проходит через точку с координатами
с угловым коэффициентом, равным .
Теорема. САУ будет абсолютно устойчива, если на плоскости видоизмененной частотной характеристики линейной части системы можно провести прямую через точку так, чтобы располагалась справа от этой прямой. Указанную прямую принято называть прямой Попова.
с угловым коэффициентом, равным .
Теорема. САУ будет абсолютно устойчива, если на плоскости видоизмененной частотной характеристики линейной части системы можно провести прямую через точку так, чтобы располагалась справа от этой прямой. Указанную прямую принято называть прямой Попова.
УГАТУ-2015
Слайд 33Второй метод Ляпунова
не требует нахождения решения дифференциального уравнения
основная идея
замена анализа решений
нелинейных уравнений произвольного порядка на оценку свойств этих решений с помощью дифференциального неравенства
УГАТУ-2015
Слайд 34исследуется изменение «расстояния» в пространстве состояний от текущей точки системы до
начала координат
В качестве оценки расстояния можно использовать скалярную функцию, которую обозначим через V(x)
фазовые траектории системы
устойчивое состояние равновесия -«стягиваются»
В качестве оценки расстояния можно использовать скалярную функцию, которую обозначим через V(x)
фазовые траектории системы
устойчивое состояние равновесия -«стягиваются»
УГАТУ-2015
Слайд 35Суть второго метода Ляпунова сводится к оценке изменения некоторой функции координат
состояния системы вдоль траекторий движения
V(x) - называют функцией Ляпунова.
V(x) - называют функцией Ляпунова.
УГАТУ-2015
Слайд 36УГАТУ-2015
а б
Рис. 1. Изменение функции V в случае устойчивой (а) и
неустойчивой (б) систем
Функция V(x) называется положительно определенной в области D, если выполняются свойства
(8.14)
Слайд 37УГАТУ-2015
Полной производной функции Ляпунова в силу системы называется функция
–
вектор-строка частных производных.
в развернутой форме
Слайд 38Теоремы второго метода Ляпунова
Состояние равновесия системы является асимптотически устойчивым, если для
положительно определенной функции Ляпунова V(x) ее полная производная в силу системы есть отрицательно определенная функция, т. е. при выполнении условий
УГАТУ-2015
Слайд 39Теорема о неустойчивости
Состояние равновесия системы является неустойчивым, если для положительно
определенной функции Ляпунова V(x) ее полная производная в силу системы представляет собой также положительно определенную функцию.
теоремы дают только достаточные условия устойчивости и неустойчивости
теоремы дают только достаточные условия устойчивости и неустойчивости
УГАТУ-2015
Слайд 40Пример
с помощью второго метода Ляпунова оценить устойчивость системы, поведение которой
описывают следующие уравнения:
Полагаем u = 0 и рассмотрим автономную систему
Полагаем u = 0 и рассмотрим автономную систему
УГАТУ-2015
Слайд 41Выберем для нее в качестве функции Ляпунова следующую функцию:
Определим теперь полную
производную функции Ляпунова вдоль траектории движения автономной системы
обращается в нуль не только в начале координат, но и на всей оси .
обращается в нуль не только в начале координат, но и на всей оси .
УГАТУ-2015
Слайд 42
полная производная новой функции Ляпунова есть отрицательно определенная функция.
Следовательно, исходная
система является асимптотически устойчивой.
УГАТУ-2015
