- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Начертательная геометрия. Пересечение линии и поверхности презентация
Содержание
Слайд 1Начертательная геометрия Семинар №12 Пересечение линии и поверхности. Подготовили: Данилова У.Б., Елисеева О.И. Московский
Слайд 2Задача 75-в. Построить проекции точек пересечения прямой а с поверхностью сферы.
1.
2. Находим линию пересечения m плоскости g с поверхностью сферы.
3. Точки пересечения m с прямой а – искомые.
f0g
m’’
m’
K1’
K2’
K1’’
K2’’
Слайд 3Задача 77а. Построить проекции точек пересечения прямой а с поверхностью тора,
В’’
В’’пов
В’пов
К2’пов
К1’пов
aвр.В
aвр.К1
aвр.К2
i’’
i’
В’
К2’
К2”
К1’
К1”
1. Ось вращения тора будет осью, вокруг которой надо повернуть прямую а, чтобы прямая оказалась в одной плоскости с заданной окружностью-образующей тора .
2. Вращаем точку В, принадлежащую прямой а.
3 Повернутая прямая пересекает окружность тора в точках К1 пов. и К2 пов.
4. Находим соответствующие проекции точек пересечения проведя плоскости вращения, а, затем, линии связи.
Слайд 477-б. Построить проекции точек пересечения прямой а с конической
(без построения лекальных кривых)
1. Заключаем прямую а в плоскость a, проходящую через вершину конуса:
Задаем прямую в, проходящую через вершину S и пересекающую прямую а в точке 1.
2. Находим прямую пересечения плоскости a с плоскостью основания конуса.
4. Точки пересечения линий пересечения с заданной прямой а – К1 , К2 – искомые.
1’’
1’
в’
Нв’’
На’’
Нв’
На’
h0a
a
2’
3’
2’’
3’’
К1’’
К2’’
К1’
К2’
a
в’’
3. Находим линии пересечения плоскости a с конической поверхностью.
l1’’
l2’’
l1’
l2’
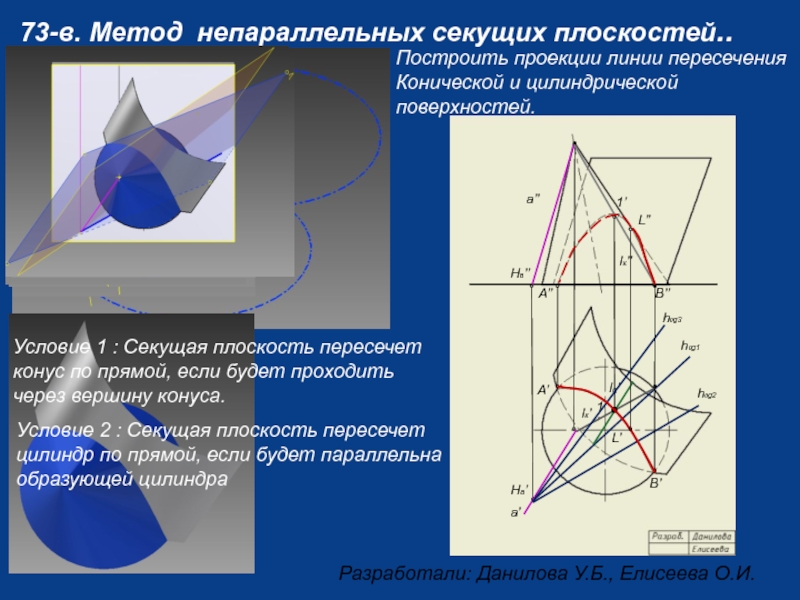
Слайд 573-в. Метод непараллельных секущих плоскостей..
Построить проекции линии пересечения Конической и цилиндрической
Условие 1 : Секущая плоскость пересечет конус по прямой, если будет проходить через вершину конуса.
Условие 2 : Секущая плоскость пересечет цилиндр по прямой, если будет параллельна образующей цилиндра
На’
На’’
h0g1
1’
а’’
lц’
lк’
а’
lк’’
1’’
h0g2
h0g3
A’
A’’
В’
В’’
L’
L’’